Модели и методы адаптивного выбора управленческих решений на основе системного анализа промышленных рисков горного предприятия

Современная деятельность отечественных горных предприятий характеризуется определенной экономической нестабильностью и высоким динамизмом внешней социально-экономической среды, обусловленными ориентацией в основном на внешние рынки сбыта, низкой конкурентоспособностью отечественных потребителей, недостаточной инвестиционной активностью большинства горных предприятий, отсутствием в ряде случаев полной и актуальной прогнозной информации о направлениях изменения рыночной конъюнктуры, влиянием на эффективность производственно-хозяйственной деятельности большого количества неконтролируемых, плохо контролируемых и неопределенных факторов. В связи с этим в горной промышленности подавляющее большинство управленческих решений объективно принимается в условиях неопределенности и различных видов функциональных рисков [1].

Анализ и управление рисками одно из основных направлений теории управления сложными социальными и экономическими системами, необходимость развития которого обусловлена сложностью структуры промышленных предприятий как объектов управления риском и высоким уровнем неопределенности внешней социально-экономической и внутренней среды предприятий. Актуальность разработки и применения методов анализа и управления рисками в горной промышленности особенно возросла в последние годы в связи с глобализацией, вступлением России в ВТО и существенным влиянием мировой финансово-экономической нестабильности на деятельность промышленных предприятий, современные бизнес-процессы которых не позволяют обеспечить быструю адаптацию характеристик производимой продукции и производственных программ.

Принятие решений по анализу и управлению рисками объективно осуществляется в условиях различного вида неопределенностей, которые объективно присущи факторам внешней и внутренней среды предприятия, а также параметрам и характеристикам сложных недетерминированных производственно-технологических процессов и бизнес-процессов горнопромышленных предприятий. Неопределенность при управлении рисками это неполнота, неточность или недостоверность информации об условиях и параметрах функционирования недетерминированных производственнотехнологических процессов; о характеристиках и условиях реализации бизнес-процессов; о возможностях возникновения неблагоприятных ситуаций в деятельности предприятия; о причинах и источниках рисков; о параметрах внешней и внутренней среды организации; о величинах причиняемых ущербов, потерь или убытков. Для формализации различных видов неопределенностей при решении экономико-математических задач управления рисками необходимо использовать теорию экспертных оценок, теорию нечетких множеств и нечетко-логического вывод.

При учете рисков горнопромышленного предприятия необходимо учитывать, что нестабильная внешняя и внутренняя среда предприятия представлена как набор системных факторов внешней и внутренней среды, которые при определенных условиях приводят к возникновению факторов (источников) риска [2]. Примером набора таких неопределенных и нестабильных факторов (источников) риска горнопромышленного предприятия могут являться: неопределенные изменения параметров производственных мощностей и технологических режимов предприятия; уровень пожаро-, взрыво- и технической опасности технологических процессов; степень износа оборудования; нарушения в работе системы всеобщего управления качеством; система организации технического обслуживания и ремонта оборудования; изменения характеристик рынков сбыта и потребителей; волатильность цен на сырье, и материалы; изменения в государственном стимулировании торговли; введение таможенных ограничений; недостаток квалифицированных кадров; снижение платежеспособности потребителей; рост уровня конкуренции; появление товаров-заменителей и т.д.

В результате неопределенности факторов (источников) риска, обусловленных влиянием внешних системных факторов среды на производственную, предпринимательскую, финансовую и природоохранную деятельность горного предприятия, возникают опасные (рисковые) ситуации, которые вызывают вредоносный и деструктивный ущерб. При этом существование опасной ситуации определяется на основе сопоставления величины каждого фактора (источника) риска с его целевым значением. Другими словами, если величина фактора риска не превышает допустимого уровня, то говорить о возникновении опасной ситуации нецелесообразно. В случае если же величина фактора риска превышает целевой уровень, то опасная ситуация существует, и требуется применить методы управления рисками с целью снижения возможных ущербов и убытков [3].

С этой целью в статье разработан подход выбора управленческих решений на основе системного анализа промышленных рисков горного предприятия.

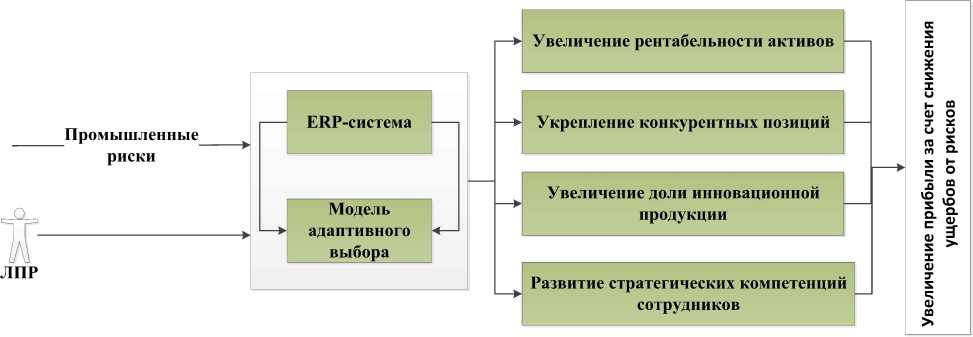
Рис.1 Схема взаимодействия модели адаптивного выбора с существующими системами управления на предприятии

Ежедневно руководству горнопромышленных предприятий необходимо решать задачи стратегического планирования и/или оперативного управления, учитывая определенный уровень промышленных рисков. Так как в системах управления предприятиями обычно используются ERP- или APS-технологии, то выбор управленческого решения в условиях риска можно структурно представить моделями математического программирования [4; 5].

В задачах математического программирования предпочтения ЛПР, действующего в условиях риска, на множестве альтернатив определяются целевой функцией. Априорная или текущая критериальная неопределенность заключается в том, что коэффициенты целевой функции неизвестны или известны неточно вследствие влияния промышленных рисков горного предприятия. Их необходимо оценить по наблюдениям за принятыми ЛПР решениями [6; 7].

Пусть ЛПР, действующее в условиях риска, принимает решения в K ситуациях. Всякий k-й раз ( k 1, K ) можно наблюдать тройку элементов (s k , d k , L k ), где s k - состояние или ситуация, требующая принятия решения в условиях риска(СТПР), d k - решение, принятое в данной ситуации s k , L k -эффект от принятого ЛПР решения (измеряется не в абсолютной шкале, а в относительной бинарной - хорошее/плохое). По этим наблюдениям необходимо восстановить вектор коэффициентов целевой функции c , т.е. построить вектор оценок с . Без потери общности учитываются только наблюдения с хорошими (правильными) решениями, принятыми в условиях риска.

Для этого задача линейного программирования из различных форм ее представления используется в следующем виде: n

L ( c , x ) c^Tx     c x max ,                           (1)

j 1                    xj где x = Х1 x2 ... xnT - вектор переменных размерности n , на которые накладываются следующие ограничения (представляющие собой СТПР), вызванные наличием промышленных рисков горнопромышленного предприятия:

ⁿ a ij x j    a i 0    0; i 1, m ;                                       (2)

j 1

x _j 0; j 1, n                                      (3)

c = [ c 1   c 2  • •   c n ] T - вектор параметров целевой функции;

A a - матрица коэффициентов системы ограничений размерно-ij mn сти m n , которую можно представить, как совокупность уровней промышленных рисков горнопромышленного предприятия;

a 0 ⁼[ a₁₀ a 20 • a m ₀ ] T - вектор свободных членов системы ограничений, показывающий возможный ущерб совокупности уровней промышленных рисков.

В этой прямой постановке задачи линейного программировани я (ПЗЛП) традиционно предполагаются известными матрица A , векторы c и a , необходимо найти вектор оптимального решения x ^*.

Критериальная неопределенность означает, что вектор c неизвестен. Задача построения оценки c вектора c по наблюдениям названа обратной задачей линейного программирования (ОЗЛП). Обратная задача выполняет функцию контура обратной связи для подстройки параметров модели по текущим предпочтениям ЛПР и решается при следующих предпосылках:

• 1.    Используются только «хорошие» решения ЛПР, действующего в условиях риска.

• 2.    Существует только критериальная неопределенность, учитывающая возможное влияние определенного вида риска.

• 3.    Решение ЛПР совпадает хотя бы с одной из крайних точек области допустимых решений (ОДР).

• 4.    Предпочтения ЛПР стационарны.

• 5.    Характеристики внешней среды стационарны.

• 6.    Предпочтения ЛПР детерминированы (воспроизводимы).

Отклонение от этих предпосылок не приводит к потере работоспособности предложенных алгоритмов, а лишь несколько снижает скорость настройки модели. Алгоритмы решения ОЗЛП построены на основе геомет- рической интерпретации и представлены в итерационной форме. Укруп-ненно процедуры решение ОЗЛП и ПЗЛП приведены на рис.2 и рис. 3.

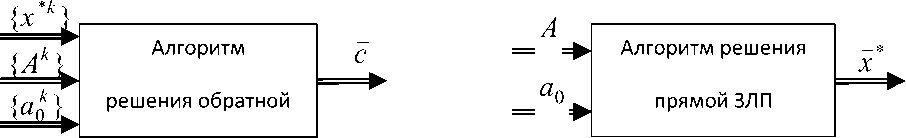
Рис. 2. Процедура решения ОЗЛП     Рис. 3. Процедура решения ПЗЛП

Алгоритм решения ОЗЛП представлен в виде одношаговой и рекуррентной процедур. Одношаговый алгоритм выполняется в виде последовательности действий:

Этап 1. Для каждого k-го набора данных (наблюдения) по принятому ЛПР решению Х^к из системы неравенств выделить M неравенств (активных ограничений, выраженных определенным уровнем каждого вида промышленного риска), обратившихся в точке x^k в равенства.

Этап 2. Для каждой активной гиперплоскости каждого наблюдения вычислить координаты нормальных векторов единичной длины (НВЕД)

^ei •

Этап 3. Для каждого k-го наблюдения (по множеству его активных ограничений, характеризующих уровень риска) вычислить средний НВЕД e k и его вес р^к е [0,1].

Этап 4. Вычислить средневзвешенный НВЕД по всем K наблюдениям.

В итоге по K наборам данных вектор оценок параметров целевой функции с примет вид с =[ e K e K • e K ] T , тогда оценка целевой функции может быть представлена как:

n

n

L K ^{( x} ) = c K ^xx j ⁼ eL j x j .

j =1

j =1

Эта целевая функция используется для решения ПЗЛП. В рекуррентной форме алгоритма в качестве меры точности восстановленных оценок коэффициентов целевой функции используется величина дисперсии рас- сеяния оценок относительно скользящего среднего.

Оценивание значимости частных критериев в общем эффекте управления является важным вопросом, возникающим при управлении предприятием в условиях промышленного риска. Потребность в подобных задачах возникает при оценивании значимости статей затрат, выявлении узких мест, определении вклада подразделений в общий эффект, определении объектов инвестирования и т.п.

Эффект обычно представляет собой комплексный показатель, учитывающий возможные риски на горном предприятии, интегрирующий в себе множество частных показателей (прибыль, рентабельность, производительность, себестоимость, продолжительность цикла производства и т.п.). Именно такой интегральный показатель L(X) и является обобщенным откликом, функционально связанным с переменными x пространства решений.

Применение адаптивного подхода к управлению (выбору решений) на основе настраиваемых моделей математического программирования, позволяет получить весовые коэффициенты значимости частных показателей (критериев), в том числе и уровень рисков, автоматически, без привлечения экспертов (в отличие от традиционных подходов), причем в динамике их реальных изменений. В качестве скалярной свертки частных показателей в интегральный используется взве шенная сумма целевых функций с соответствующими весами Д, h = 1, H . Целевая функция (1), как скалярная свертка взвешенных частных целевых функций, представлена в виде:

L ( c , ^x ) = ^A L h ( c h . ^x ) = ^ЛЁ с / Л , = Ё( Z^ c ,* ) X j = £ с_Л ^max • (⁵) h =1 h =1 j =1 j =1 h =1 j =1 ^{X j}

Задача оценивания вклада каждого вида промышленного риска в общий эффект заключается в следующем. Пусть известны коэффициенты c_h частных линейных целевых функций L_h ( c_h , x ), h = 1, H и коэффициенты c. интегральной целевой функции L ( c , x ). Необходимо определить весовые коэффициенты , имеющие смысл значимости или относительного вклада каждого критерия в общий эффект.

Показано, что если коэффициенты c оценивать одним из приведенных выше алгоритмов решения ОЗЛП, а c_h - одним из алгоритмов МНК-оценивания, то решение задачи сводится к вычислению оценок весовых коэффициентов p_h из следующей системы уравнений:

ZA C jh= C j. , j = 1, n . (6) h =1

В случае если эта система уравнений переопределена ( n H ), для вычисления p_h следует воспользоваться одним из алгоритмов МНК-оценивания.

Применение такого подхода позволяет автоматически непрерывно вести мониторинг вклада различных промышленных рисков в общий эффект работы предприятия или структурного подразделения.

Инвестиционная оценка предложенной в статье модели адаптивного выбора управленческого решения в условиях риска требует введения следующих параметров: R1 - риски, снижающие величину денежного притока от реализации проекта; R2 - риски, увеличивающие первоначальные инвестиционные затраты и периодические денежные оттоки, связанные с реализацией проекта; R3 - риски внешней среды, снижающие общую стои- мость денег, а следовательно и увеличивающие ставки дисконтирования проекта. Тогда расчет чистого приведенного дохода (NPV) от инвестици- онных проектов с использованием модели адаптивного выбора определя- ется следующим образом:

MN

NPV '

j 1 i 1

( Bx i^j ( R 1 ^ji ) Вых i^j ( R 2 ^ji )) (1 + r ( R 3 i )) ⁱ

где M -количество инвестиционных проектов; N - период расчета; Вх i (R 1i ) -денежный приток от реализации инвестиционного проекта с учетом влияния рисков R 1 ; Вых i (R 2i ) -денежный отток при реализации проекта, с учетом влияния рисков R 2 ; r(R 3i ) -ставка дисконтирования проекта с учетом влияния рисков R3. Тогда оценка экономической эффективности равна:

ΔNPV= NPV’– NPV, (8)

где NPV’– значение чистого приведенного дохода, рассчитанное с учетом реализации адаптивного подхода по управлению рисками; NPV – значение чистого приведенного дохода, рассчитанное без реализации дан- ного подхода по управлению рисками.

Расчет изменения стоимости компании (СК) при использовании адаптивного подхода

N

CK = 2

i 1

EBIT i { R 1 , R 2 }(1   tax )  ( CAPEX { R }   A i { R 2 }) -A WC i { R 1 , R 3 }

(1 + r(R3))i где EBIT (earnings before interest and taxes) — прибыль до вычета налогов и процентов по кредиту с учетом рисков R1 и R2 в период i; tax — эффективная ставка налогообложения в период i; CAPEX (capital expenditures) — инвестиционные затраты на основные фонды, а также затраты по обслуживанию кредитов с учетом рисков R2; ΔWC — изменение оборотного капитала с учетом рисков R1 и R3; А -амортизационные отчисления.

Реализация предлагаемой в статье модели было апробировано на одном из угледобывающих компаний на инвестиционного организационнотехнологическом проекте по проведению комплекса воздухоочистительных мероприятий, реализуемых до использования системы улавливания неорганизованных вы-бросов. Проведенные автором расчеты показывают, что NPV проекта составит 5,85 млрд. руб.

С использованием предложенной модели адаптивно выбора управленческих решений в условиях риска были проанализированы основные функциональные риски предприятия и рассчитаны их уровни: финансовый риск - 6%; инвестиционный риск -15%, коммерческий риск - 5%, производственно-технологический риск - 21%, природоохранный риск - 13%.

Также был выбран и реализован ряд мероприятий по управлению выделенными видами риска, к числу которых относится внедрение концепции всеобщего управления качеством «6σ», применение которой основано на использовании целого ряда вероятностно-статистических методов, и подразумевает создание на предприятии определённой группы высококвалифицированных специалистов по управлению качеством (так называемые специалисты «чёрного и зелёного пояса»).

Показано, что при использовании модели чистый приведенный доход реализации проекта в результате увеличился на 1,38 млрд. руб.

Таким образом, в статье показана необходимость создания модели адаптивного выбора управленческого решения в условиях риска. Показана возможность встраивания модели в существующую систему управления на промышленном предприятии. Представлена математическая модель принятия оптимального управленческого решения ЛПР, действующего в условиях рисков. При этом оценено влияние принятого решения на показатели эффективности функционирования предприятия.

горнопромышленное предприятие, промышленные риски, управленческое решение, условия неопределенности, показатели эффективности mining factory, industrial risks, management decision, conditions of uncertainty, efficiency index