Модели и методы механизмов ценообразования медицинских услуг в условиях конкурентного взаимодействия

Конкуренция, как фактор рыночной экономики, присуща любым отраслям и их предприятиям. Медицинские учреждения в этом смысле не являются исключением. Несмотря на уникальность деятельности медицинских учреждений, предмета труда (человек, его здоровье) следует отметить, что эти учреждения работают в реальной рыночной действительности, диктующей необходимость обеспечения эффективности функционирования.

Как известно рыночная среда предусматривает экономические взаимодействия производителей и потребителей продукции (услуг). Рассматривая взаимодействия производителей (медицинские учреждения) и потребителей (население) на территории некоторого региона, имеет место замкнутая система.

Следует также отметить, что бюджетное финансирование системы здравоохранения в настоящей момент, не в состоянии обеспечить достаточное финансирование медицинских учреждений (оплата труда, средство на модернизацию оборудования, мероприятия по повышению квалификации и профессионального уровня персонала и т.д.). Таким образом, спрос на медицинские услуги, а в особенности высококачественные, существенно превышают возможности медицинских учреждений в рамках, выделяемых со стороны государства бюджетов. Следствием этого явилось формирование в нашей стране системы платных медицинских услуг:

. частные клиники, лаборатории;

дений, осуществляемых сверх нормативной загрузки по бюджетному финансированию.

Рассматривая сложившуюся ситуацию можно констатировать, что руководство любого медицинского учреждения функционирует в реальной экономической, конкурентной среде и для «выживания» в этой среде необходимо использование современного аппарата теории управления, позволяющего решать задачи по обеспечению эффективного их функционирования.

Основным инструментом конкурентной борьбы является цена на услуги и предлагаемое их качество. Отметим также, что население конкретного региона и, соответственно, спрос на услуги есть некоторая статистическая константа.

Смоделируем и проанализируем модели ценовой конкуренции между этими ЛПУ (лечебно профилактическое учреждение) при постоянном спросе на медицинские услуги.

Имеет место система, включающая в свой состав n медицинских учреждений, оказывающих однотипные медицинские услуги с фиксированным качеством Q . Общая схема взаимодействия представлена на рис. 1.

Целевая функция i -го ЛПУ при этом будет иметь следующий вид:

F ⁽ Q, p ) = AD i ⁽ p )( P i - c i ) - ^kQ ^p , ⁽¹⁾ где А – общий спрос на услуги, имеющий место на рынке;

Di – доля рынка iго игрока (исполнителя);

ci – себестоимость услуги iойорганизации;

k і 0 – неотрицательный коэффициент, отражающий затраты на обеспечение качества;

p = ( р1, р2, …, рj ) – вектор цен на услугу.

Предположим, что ЛПУ разыгрывают игру в нормальной форме, т.е. выбирают цены на оказываемые услуги одновременно и независимо.

Обозначим X — степень конкурентоспособ-

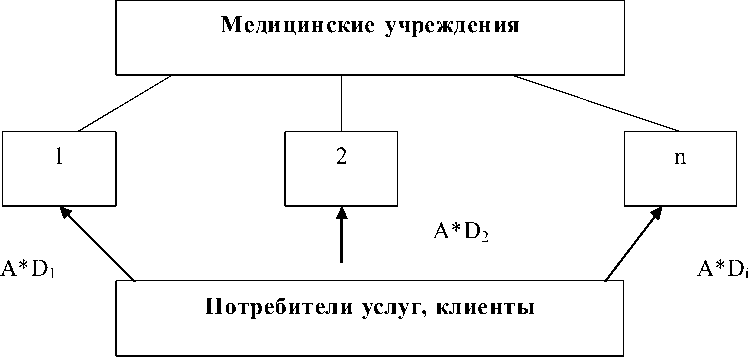
Рис. 1. Система оказания медицинских услуг

ности по цене, Л >  0. При Л =0, спрос делится между всеми ЛПУ равномерно.

Примем, что

1    f s P j    1

D i = " + л     . "  P i

n n -1

V 7

Откуда следует, что

Л —

D i

fE pj j * i n -1

- p_i

Дифференцируя целевую функцию (1) по цене и с учетом (2) соответственно, и приравнивая производную к нулю, получим:

^c i ¹

Pi I+

F ‘    Л  Лп

E Pj j e N 2(n -1)

Просуммировав выражение (4) по всем ЛПУ и

обозначив p

E

^— E P j j e N

c E

E c i получаем:

PE

— h C vi Л ^E .

Интегрируя (4) и (5) получим выражение равновесных по Нэшу значений цен:

* n -1

Pi — c +----- i i 2 n -1

n - 1

E c j ^- c i

+In • (6)

Модель (6) позволяет количественно оценить снижение равновесной цены с увеличением количества ЛПУ на рассматриваемой территории,

а также показывает то, как влияет увеличение себестоимость медуслуги ci, оказываемое в i-ым ЛПУ на рост равновесной цены.

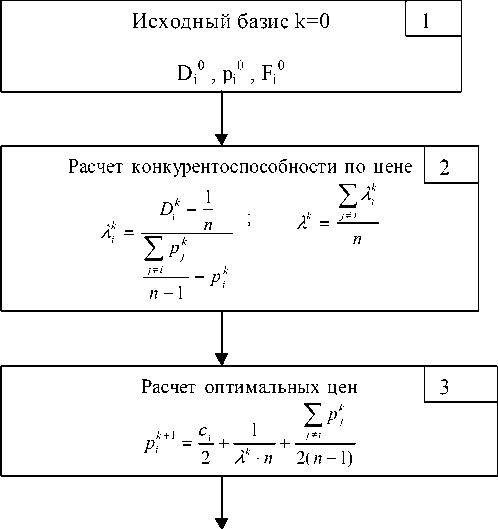
Следует отметить, что информация о равновесных состояниях необходимая руководству лечебных учреждений недостаточна, с точки зрения оперативного управления. Речь идет о том, что равновесные состояния достигаются в результате достаточно большого количества «шагов», т.е. совокупности принимаемых управленческих решений и получаемых результатов множеством игроков, участников рыночных взаимодействий. Если конкретизировать сказанное через призму исследуемого объекта, а именно замкнутого рынка медицинских услуг можно утверждать, что имеет место игра, в которой каждый из участников взаимодействия (руководство конкретного ЛПУ) при определенных шагах выбирает свои решения. При выборе этих решений он стремится оптимизировать свою функцию цели (критерий оптимальности). Получаемый результат, однако, зависит не только от выбора конкретного субъекта, но и от тех решений, которые выбирают другие участники рынка (конкуренты). Таким образом, равновесные состояния, модели оценки которых рассматривались выше, достигаются в процессе неоднократного проигрывания процедур: принятие решений – результат – анализ – принятие решений и т.д. следовательно, «выход» в точку равновесия системы из исходного состояния сопровождается реализацией нескольких этапов функционирования. Выбор решений на каждом этапе при этом представляет самостоятельную задачу. На рис. 2 представлен разработанный нами алгоритм принятия решений по ценообразованию в условиях конкуренции.

Проиллюстрируем работоспособность предложенных моделей и алгоритмов принятия решений на конкретном примере.

Пусть имеется некоторый базис, характеризующийся следующими исходными параметрами (k=0).

Оценка доли рынка

D ^{+ 1} = 1 + _л

n

fV k + 1 L p,

^— n -1

V

л

pi

V

Оценка экономических результатов k+1

F^{k + 1}

= A

¹ + Л^к

fE p, .^±_ n -1

^- Pi

_f k + 1

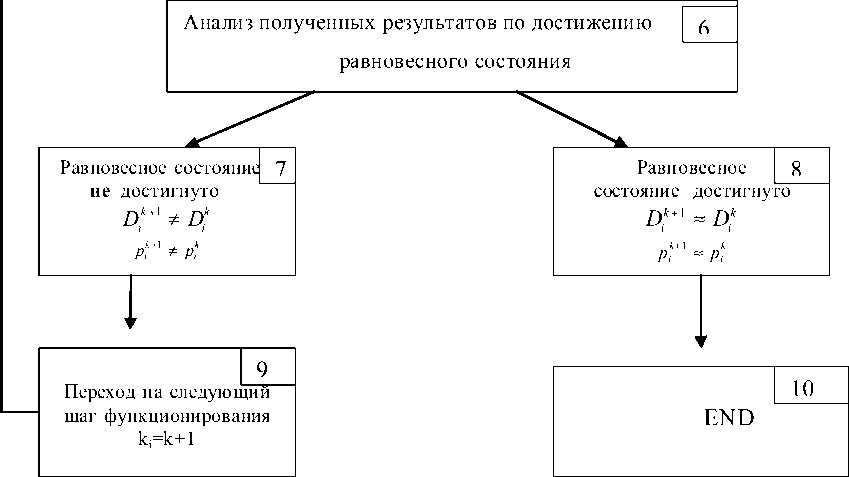
Рис. 2. Алгоритм принятия решений

Пусть

p1 = 30 ;	p2=33;	p3 = 40;
А=300; c1 = 25 ;	c2 = 26;	c3 = 34 ;
D1 = 0,45;	D2 = 0,36;	D3 = 0,19

Используя модель (3), рассчитаем показатель конкурентоспособности по цене. Отметим при этом, что данный показатель является общим для всех 3-х участников взаимодействия, которые рассматриваются в примере.

Поэтому рассчитываем частный показатель конкурентоспособности.

0,45 0,33 _ 0,018;

36,5 - 30

1 1 73 25 p1 _ + + _ 51,5 0,016 • 342 1 70 26 p12 _ — + +—_ 51,3 0,016 •3 4 2 p 3 _

1 63 34 --1---1-- _ 53,5 .

0,016 • 3 4 2

Доля рынка распределится следующим образом:

D. _ ¹ + 0,016 | ^{51,3 + 53,5} - 51,5 | _ 0,35 ;

1 3         ( 2             )

0,36 - 0,33 = 0,015;

35 - 33

D, _ ¹ + 0,016 | ^{51,5 + 53,5} - 51,3 | _ 0,35 ;

2 3         (     2            )

⁰¹⁹ - 0,33 = 0,016 .

31,5 - 40

D₃ _ ¹ + 0,016 | ^{51,5 + 51,3} - 53,5 | _ 0,30 .

³3         ( 2             )

Итоговая оценка конкурентоспособности будет определяться как среднее арифметическое локальных показателей.

X _

л + X 2 + X 3 _ 0,018 + 0,015 + 0,016 n 3

_ 0,016 .

Напомним, что руководитель конкретного iго учреждения на каждом (k+1)ом шаге функционирование, принимает управленческое решение по выбору цены услуги pik+1.

На первом шаге получаются следующие результаты:

Соответственно каждый участник взаимодействия получит следующий результат:

F11=2782 , F21= 2656,   F31= 1755.

Продолжая расчеты по следующим шагам функционирования, получаем результаты, отра-женныеы в табл. 1.

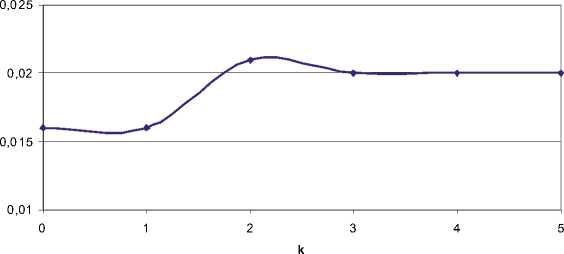
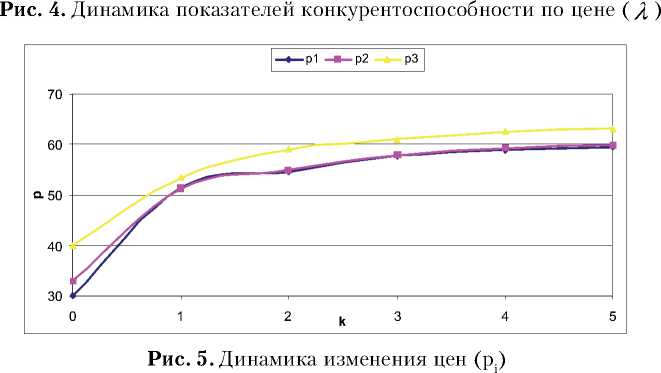
С целью наглядного представления полученных результатов, на рис. 3-5 представлена динамика изменения показателей по шагам функционирования.

Таким образом, проведенные расчеты и полученные при этом результаты наглядно проил-

Таблица 1. Сводные данные взаимодействия участников в процессе функционирования

№ шага (k)	p 1	p 2	P 3	X	D 1	D 2	D 3	F 1	F 2	F 3
0	30	33	40	0,016	0,45	0,36	0,19	675	756	342
1	51,5	51,3	53,5	0,016	0,35	0,35	0,30	2782	2656	1755
2	54,5	55	59	0,021	0,38	0,37	0,25	3383	3219	1875
3	57,7	58	61	0,02	0,37	0,36	0,27	3629	3456	2187
4	58,8	59,3	62,5	0,02	0,37	0,36	0,27	3752	3596	2308
5	59,5	59,9	63,1	0,02	0,37	0,36	0,37	3829	3640	2357

D1 D2 D3

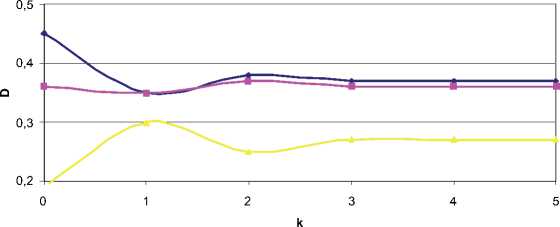
Рис. 3. Динамика доли рынка (D_i)

люстрировали работоспособность предложенных моделей и алгоритма функционирования медицинских учреждений, осуществляющих свою деятельность в конкурентных условиях.