Модели комплексной обработки радионавигационных сигналов при их обнаружении в условиях мешающих отражений на фоне флюктуационного шума

Актуальность проблемы обнаружения навигационных сигналов в радиотехнических системах (РТС) ближней навигации на основе псевдоспутников обусловлена наличием в радиоканалах так называемых мешающих сигналов, порожденных отражением радиоволн от посторонних предметов, границ раздела сред и от различных неоднородностей на трассе их распространения [1–4]. При этом мешающие сигналы представляют собой суперпозиции собственных копий сигналов, сдвинутых в общем случае хаотично по времени и частоте, которые при взаимодействии с основным сигналом вызывают его интерференционные замирания [5–7]. Если при значительном временном перекрытии мешающий сигнал окажется в противофазе с основным сигналом, то это приведет к резкому уменьшению амплитуды основного сигнала и, следовательно, к уменьшению вероятности обнаружения сигнала на фоне флюктуационного шума. А поскольку начальная фаза мешающего радиосигнала, как правило, является случайной величиной, равновероятно распределенной в интервале [–π, π], то это обстоятельство в конечном итоге приведет к существенному снижению помехоустойчивости (достоверности) обнаружения основного навигационного сигнала [5].

При этом если начальная фаза мешающего радиосигнала, обусловленная его случайным временным сдвигом, изменяется медленно, то и замирания результирующего сигнала будут – 143 – медленными, а если начальная фаза изменяется быстро и дополнительно к этому заметно влияют дестабилизирующие факторы радиоканала, то и замирания результирующего сигнала будут быстрыми.

При медленных замираниях для повышения достоверности обнаружения сигнала необходимо использовать частотно-временной резерв радиоканала, который можно реализовать, например, путем временного или (и) частотного разнесения элементов сигнала. А при быстрых замираниях необходимо использовать специальные сигналы с расширением спектра, так называемые широкополосные шумоподобные сигналы (ШПС) с последующей их оптимальной обработкой.

Недостатки этих способов очевидны: они требуют увеличения частотно-временного ресурса радиоканала, что не всегда возможно.

Цель данного исследования – разработка способа и соответствующих моделей обработки принимаемого навигационного сигнала, обладающих повышенной помехоустойчивостью его обнаружения в условиях мешающих отражений и флюктуационного шума без увеличения энергетических и частотно-временных ресурсов навигационного радиоканала.

Постановка задачи

Рассматривается РТС ближней навигации на основе псевдоспутников, работающая в режиме приема радиосигналов в условиях мешающих отражений и флюктуационного шума, задачей которой служит установление факта наличия или отсутствия навигационного сигнала в радиоканале по соответствующему критерию, в данном случае Неймана–Пирсона. При этом мешающий радиосигнал является сигналом со случайной начальной фазой, равновероятно распределенной в интервале [–π, π], и параметрами такими же, как и у сигнала навигационного с соответствующим перекрытием с ним по времени. Считается при этом, что отражения локализованы только на временной оси запаздываний и что последующие по времени мешающие сигналы не оказывают сколь-либо заметного влияния на данный навигационный сигнал в момент его отсчета и при принятии решения не учитываются. Полученная таким образом сигнально-помеховая реализация принимается на фоне флюктуационного шума с равномерной спектральной плотностью мощности в полосе частот радиоприема и с нормальным законом распределения мгновенных значений.

В результате взаимодействия с мешающим радиосигналом полезный радионавигационный сигнал на выходе согласованного фильтра искажается и существенно отличается по своей форме от формы корреляционной функции выходного флюктуационного шума согласованного фильтра соответствующего приемника. Данное обстоятельство позволяет использовать комплексную обработку радионавигационного сигнала при его обнаружении в условиях мешающих отражений на фоне флюктуационного шума.

Под комплексной обработкой навигационного сигнала при наличии мешающих отражений понимается его двухканальная обработка, в первом (основном) канале которой осуществляется согласованная фильтрация сигнала с последующим принятием решения о его наличии или отсутствии, а во втором (дополнительном) канале решение о наличии или отсутствии сигнала принимается по выходному сигналу того же согласованного фильтра, но относительно значения шума, измеренного в опорном отсчете. При этом момент опорного – 144 – отсчета определяется точкой пересечения огибающих основного (навигационного) и мешающего радиосигналов и при значительном их временном перекрытии находится в непосредственной близости с моментом информационного отсчета, что обусловливает высокую корреляцию флюктуационного шума между этими отсчетами. По значению шума, измеренного в опорном отсчете, устанавливается значение управляемого порога во втором (дополнительном) канале обработки. В результате итоговое решение о наличии или отсутствии сигнала принимается на основе двух частных решений по правилу: сигнал обнаруживается, если хотя бы в одном из частных каналов обработки он регистрируется (выше соответствующего порога), в противном случае принимается решение об отсутствии сигнала в радиоканале.

Принятые допущения не накладывают принципиальных ограничений на общность постановки задачи и отражают достаточно реальный режим работы навигационной РТС по обнаружению навигационного сигнала в условиях мешающих отражений и флюктуационного шума. При этом в зависимости от характера изменения начальной фазы навигационного сигнала рассматриваются модели его когерентного и некогерентного обнаружения.

Когерентное обнаружение

При когерентном обнаружении предполагается, что начальная фаза навигационного сигнала точно известна и без потери общности решаемой задачи принимается равной нулю. При этом в общем случае обнаруживаемый выходной сигнал согласованного фильтра приемника будет иметь вид ui(t) = U1(t)cos®ot, 0 < t < T,                                        (1)

где U i ( t ), to₀, T - огибающая частота и длительность навигационного радиосигнала [8].

Мешающий радиосигнал на выходе фильтра, перекрытый во времени с основным радиосигналом, будет равен u2(t) = U2[t - (t0 ± At)]cosю0[t - (t0 ± At)], t0 ± At < t < T +t0 ± At,

где U ₂( t ), 1 ₀, ±A t - соответственно огибающая мешающего радиосигнала, постоянная составляющая времени задержки и случайный временной сдвиг.

В момент отсчета при t = 0 амплитуда сигнала, определяемого суммой сигналов (1) и (2), по которой принимается решение, будет равна

U рез (0,V) = 7 U 12 (0) + U 2² [ - T (1 - х)] + 2 U 1 (O) U 2 [ - T (1 - X)]cos(V — Ф о ) х

х sin

^U 1 ^{(0) + U} 2 ^[ — ^{T (1} - X^)]c0s(Ф о — V) arctg

^U 2 ^{[ - T (1 -} X^)]sin(P o ^- V)

где x = 1 — 1 о / T — относительное перекрытие навигационного и мешающего сигналов; ф₀ = ю₀ t ₀ - постоянная начальная фаза; v = ®₀(±А t ) - случайная фаза, изменяющаяся по равновероятному закону в интервале [–π, π].

С учетом (3) вероятность правильного обнаружения сигнала при заданной вероятности ложной тревоги P 1 F в первом канале обработки, в котором используется известное одноканальное обнаружение, в наших обозначениях будет равна

P d (_V) = 1 - Ф ^Ф — 1 (1 — P f )

-

U рез (0, V) ---------------1           ----------f ,

7 Р Ш J

где Φ^–1(∙) – функция, обратная интегралу вероятности; P _ш – мощность флюктуационного шума на выходе согласованного фильтра [8].

В этом случае порог принятия решения является постоянной величиной и определяется известным выражением [8]

П = хрФ (' - Pf ).(5)

Для нахождения вероятности правильного обнаружения сигнала во втором канале обработки необходимо определить момент опорного отсчета т0 из условия равенства огибающих основного и мешающего радиосигналов:

U (t) = U [t - T (1 - х )]

В общем виде решение уравнения (6) будет следующим:

Т0 = F [T (1 - X ) а!,..., а n ,e1„.„ e m ],'

где F (•) - некоторая функция, зависящая от формы сигналов; a_b...,a „ и вь---,в m — параметры, характеризующие форму навигационного и мешающего сигналов соответственно.

Значение т₀ определяется с точностью до целого числа периодов коэффициента корреляции шума r (т₀) на выходе согласованного фильтра.

Остаточная мощность выходного шума согласованного фильтра в момент информационного отсчета относительно опорного будет равна [9]

Р ш ост = Р ш [1 - Г ²(Т о )] .                                                   (8)

При этом остаточная амплитуда сигнала в момент принятия решения определяется выражением

..... ^U ~⁽⁰ '^ = ^U Рез ⁽⁰ ' ’ ) "  ' ^Р-^^И где U _рез(0, v) определяется выражением (3), а U _рез(т₀, v) — результирующая амплитуда навигационного и мешающего сигналов в опорном отсчете. Эта амплитуда определяется аналогично ⁽³⁾ с учетом того, что U i ⁽ Т о ) « U 2 ^[т о ^- T ^{(1 -} X ^)] , ^{а фазовые} соотношения здесь сохраняются такими же, как и в (3). В результате, опуская промежуточные преобразования, получим

^U рез ^(Т 0 , V) = ^U 1 ^(Т 0 )V^2[1 + ^COS( Ф 0 - V ^)] sin

1 + cos(ф₀ - V) arctg ⁰

^Sin( Ф о ^- V)

С учетом (4), (8) и (10) вероятность правильного обнаружения сигнала во втором дополнительном канале обработки будет определяться следующим выражением:

P 2 D (V) = 1 -Ф^О - P F )

^U рез ⁽⁰ , V) + r ^(T 0 ^{) U} рез ( T 0 , V) 7 Р ш [1 - r ²(T o )]

В этом канале порог принятия решения является переменной величиной и определяется выражением

П (To) = r (To) u ш (To) + 7 Рш[1 - r 2( To)]Ф-1(1 - Pf ),(12)

где u _ш(т₀) - измеренное текущее значение шума в опорном отсчете [10].

С учетом (4) и (11) результирующая вероятность правильного обнаружения сигнала будет равна

PD рез (V) = 1 - [1 - РD ^Ж - P D (V)]-(13)

При этом средняя результирующая вероятность правильного обнаружения по всем значениям случайной начальной фазы ψ мешающего сигнала определяется выражением

1 п

Pd рез = у J Pd рез (V) dV-

— п

Результирующая ложная тревога в данном способе обнаружения будет иметь место в том случае, если при отсутствии сигнала помеха хотя бы в одном из каналов обработки превысит порог. При одинаковых вероятностях частной ложной тревоги в каналах обработки P 1 F = P ₂ F = P i, ₂ F результирующая вероятность ложной тревоги будет равна

P f рез = 1 - (1 - P F )(1 - P 2 F ) = 1 - (1 - Р д F Л                      (15)

Таким образом, получением результирующей вероятности правильного обнаружения сигнала и результирующей вероятности ложной тревоги заканчивается анализ данного обнаружителя.

Некогерентное обнаружение

Во многих случаях начальная фаза навигационного сигнала, как и мешающего, является случайной величиной, как правило, равновероятно распределенной в интервале [–π, π]. В этом случае необходимо использовать двухканальное некогерентное обнаружение, при котором все операции обработки сигнально-помеховых реализаций осуществляются с их огибающими. Рассмотрим эффективность данной модели обнаружения навигационного сигнала в условиях мешающего сигнала на фоне белого шума.

Пусть обнаруживаемый выходной сигнал согласованного фильтра в общем случае имеет вид

5/ t ) = Ut )cos(to₀ 1 - ф , ),                                            (16)

где ф 1 - случайная начальная фаза, равновероятно распределенная в интервале [-п, п].

При этом мешающий радиосигнал на выходе согласованного фильтра будет определяться выражением

⁵ ₂ ⁽ t ) = U ₂ ^[ t - T (1 - X)]cos(to₀ t - ф , - v - Ф о ).

Результирующие амплитуды (огибающие) сигналов в информационном и опорном отсчетах с учетом (16) и (17) будут, соответственно, равны:

A , (0, v) = 7 U 2 (0) + U П- T (1 — X)] + 2 U , (0) U , [ - T (1 - x )]cos(v - Ф о ) ; (18)

A 2 ( т о , у) = U i (T o )V2[1 + cos(_V - ф о )] .

Вероятность ложной тревоги в первом канале обработки при некогерентном обнаружении определяется известным выражением [8]

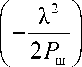
где Z - абсолютное значение порога принятия решения, а P _ш - мощность шума на выходе согласованного фильтра.

При этом вероятность правильного обнаружения сигнала в первом канале обработки, выраженная через вероятность ложной тревоги с учетом (18), такова:

H 1 D (v) = Q    ;"' , _х :н/^р

( Ршш            )

где^{Q (} x , y )^- функция ^{Маркума}.

Для получения вероятности ложной тревоги и правильного обнаружения во втором дополнительном канале обработки необходимо оперировать двумерной плотностью вероятности огибающих между информационным и опорным отсчетами при отсутствии и наличии навига- ционного сигнала.

Двумерная плотность вероятности огибающей в наших обозначениях при отсутствии сигнала имеет вид

^U 1 , U 2 , Т о ) = 2 1_² exp - ^Рш ⁽¹ R 0 )     V

U ² + U 22 ) I Г R o UU 2 ^{2 р} ш (1 ^- R 02 ) ) ⁰ [ ^р ш (1 ^- R 02 )

где I з ⁽^)^- функция Бесселя нулевого порядка, ^а R 0 = r (Т о ) [5].

Одномерная плотность вероятности огибающей по опорному отсчету представляет собой распределение Релея [8]:

Г- UI ) I ² Р ш )

® (U 2 ) = —exp P ш

При этом условная плотность вероятности по информационному отсчету относительно опорного с учетом (22) и (23) будет равна

U Lt UR ) I_o Г R u UU .

^{2 р} ш (1 ^- R , ^:) ) °L P ,(1 ^- R ,2 )

P <1 ^{- R} u )    I

С учетом (24) выражение для вероятности ложной тревоги во втором канале обнаружения будет иметь вид

2 F

U ш (T o ) R o        ^(T o )

Если зафиксировать вероятность H _{2 F} , то из (25) можно получить выражение для управляемого порога во втором канале обработки:

W = P(^

Q - H 2 F ,

U ш-oRVш (1 - Ro) J

где Q ^-1( x , у ) - функция, обратная функции Маркума.

В частном случае при R ₀ = 0 выражение (25) переходит в известное выражение (20) вероятности ложной тревоги.

При наличии навигационного сигнала плотность вероятности огибающих в информационном и опорном отсчетах будет иметь вид

W (U U т ) =   U 1 U 2   exp

²¹²⁰  P ⁽1 - R0)

U 1 + U ₂ + A + A  2 A A 2 R

^{2 Р} ш (1 - R 02 )

да

X Ув / n n=0

R ⁰ U ^{1 U 2 р} ш (1 - R o2 ).

A i ^- R o A 2 и 1

^Р ш ^{(1 -} R 0 )

Д — R Д A 2  R0 Ai т т рш (1 - R02)  :

где I n (∙) – функция Бесселя n -го порядка; ε n = 1 при n = 0 и ε n = 2 при n > 0 [5]. Плотность вероятности огибающей по опорному отсчету будет равна

W ( U 2 ) = -2 exp Р

(

—

U ₂ ² + A² ) Г U ₂ A ₂ ) 2Р I ⁰ 1 Р .

ш у V ш J

Условную плотность вероятности по навигационному отсчету относительно опорного

определим, пользуясь (27) и (28):

и

W,(- , , т₀ / U ₂) =             ¹----------exp

I 0 [ U^A ² 1 ^р ш ⁽ 1 ^— R 0^)

V ^Р ш ^у

U 1² + U 2 R p² + A² + A 2 — ² A 1 A 2 R 2 Р ш (1 — R p2 )

да

S В n l n = 0

R 0 - 1 - 2 — ^Р ш (1 — R 0^!).

I n

A 1 — R 0 A 2,;

U

^Р ш (1 — R 02 ) ¹

I n

A 2 — R 0 A 1 U Р ш (1 — R 02 )

При этом вероятность правильного обнаружения будет определяться решением следую- щего интеграла:

H 2. D = J W ( - 1 ,Т 0 / U ) d- 1 -

Х( Т 0 )

Для упрощения выражения, определяющего H2D, применяется следующий прием. Исследования показывают, что при изменении напряжения в опорном отсчете U2 плотность вероят-– 149 – ности (29) смещается по оси значений аргумента практически без деформации своей формы.

Следовательно, значение H 2 при любом U 2 = U ш ^(т 0 ) будет практически таким же, как и при U 2 = 0, при котором условная плотность вероятности ⁽2⁹⁾ принимает вид

W 2 (U 1 ,^/ U 2 ) =     _i ^U    exp

^Рш ⁽¹ R 0 )

U 12 + ( A ~ R о A 2 ) 2 ^{2 Р} ш (1 - R 2 )

I 0

A ¹ R ⁰ A ² U ^р ш (1 - R 02 ) ¹

В этом случае вероятность правильного обнаружения сигнала в соответствии с (30) с учетом (31) будет равна

H 2 D = Q

A 1 — R 0 A

λ(τ 0 )

V Р ш (1 - R 2 )' 7 Р ш (1 - R» 2 )

При отсутствии перекрытия навигационного и мешающего сигналов U ₂[- T (1 - х)] = 0 и R о = 0 и выражение ⁽³²⁾ переходит в известное выражение для вероятности правильного н^екогерентного обнаружения радиосигнала [8]:

H 2 D = Q

U 1 (0) ^, P _ш

λ

P ш

Таким образом, выражения (25) и (32), соответствующие общему случаю, являются новыми и получены в данной работе впервые.

С учетом (18), (19) и (26) вероятность правильного обнаружения сигнала во втором канале обработки, выраженная через вероятность ложной тревоги, будет равна

H 2 D ( V ) = Q

4(0, V) - R 0 A 2 ( Т 0 , V ) ,- H Т Р Шо³^

.

x ²

При получении (34) использовано равенство Q (0, x ) = exp(—2) [5].

Результирующие вероятности правильного обнаружения и ложной тревоги будут определяться общими с когерентным обнаружением выражениями (13) и (15) соответственно. При этом средняя результирующая вероятность правильного обнаружения по всем возможным значениям фазы Т будет определяться интегралом (14), который вычислялся численным методом.

Результаты исследования

Для получения количественных результатов при когерентном и некогерентном обнаружении в расчетах использовалась гауссовская форма навигационного и мешающего радиосигналов с относительным временным перекрытием χ = 0,7. Отношение сигнал-фоновый шум по мощности принималось равным h2 = 40 с результирующей вероятностью ложной тревоги PF рез = HF рез = 10 3. При этом исходная вероятность правильного обнаружения сигнала при отсутствии мешающих отражений и когерентном обнаружении составила PD исх = 0.9996, а при некогерентном обнаружении HD исх = 0.997.

В условиях мешающих отражений при постоянной составляющей начальной фазе φ 0 = ω 0 t 0 = 0 и характерных соотношениях начальных фаз между навигационным и мешающим сигналами, равных ψ = (0; π/2; π) радиан (рад) по формулам (4), (11), (13) для когерентного обнаружения и по формулам (21), (34), (13) для некогерентного обнаружения, рассчитаны и сведены в табл. 1 значения вероятностей правильного обнаружения сигнала в первом канале обработки P 1 D (ψ), H 1 D (ψ), во втором канале P 2 D (ψ), H 2 D (ψ) и результирующей вероятности P D рез (ψ), H D рез (ψ).

Из таблицы следует, что с увеличением фазового сдвига между навигационным и мешающим сигналами как для когерентного, так и для некогерентного случая вероятность правильного обнаружения в первом канале обработки уменьшается, а во втором – увеличивается. При этом результирующая вероятность правильного обнаружения с изменением фазового сдвига изменяется незначительно и при заданных исходных данных практически не уменьшается ниже P_{D рез}(ψ) = 0.999 при когерентном обнаружении и H_{D рез}(ψ) = 0.993 при некогерентном обнаружении. При этом средняя вероятность правильного обнаружения, полученная путем усреднения результирующей вероятности по всем значениям случайной фазы ψ, в соответствии с (14) при когерентном обнаружении равна P D = 0.9996, а при некогерентном обнаружении H D = 0.996, что свидетельствует о высокой эффективности данного способа обнаружения сигналов.

Такое поведение вероятностных характеристик объясняется наличием в приемнике двух каналов обработки, которые взаимно дополняют друг друга по эффективности [11]. Если в одном канале условия обнаружения ухудшаются, то во втором канале в тот же момент времени условия обнаружения улучшаются и в результате показатели итогового (результирующего) обнаружения практически не ухудшаются.

Например, если мешающий радиоимпульс находится в фазе с навигационным радиоимпульсом, то амплитуда результирующего сигнала в момент его регистрации резко возрастает. При этом достоверность обнаружения по первому каналу увеличивается, а по второму каналу уменьшается за счет возникновения составляющей сигнала (подставки) в опорном отсчете. Если мешающий радиоимпульс находится в противофазе с навигационным, то, наоборот, условия обнаружения по основному каналу ухудшаются по причине уменьшения амплитуды

Таблица. Значения вероятностей правильного обнаружения сигнала

Характеристика Значение ψ, рад 0 π/2 π P1D(ψ) 0.99999 0.9994 0.65 H1D(ψ) 0.9992 0.991 0.37 P2D(ψ) 0.023 0.674 0.9985 H2D(ψ) 0.212 0.671 0.989 PD рез(ψ) 0.99999 0.9997 0.9994 HD рез(ψ) 0.9994 0.997 0.993 результирующего сигнала в момент его отсчета, а по дополнительному каналу условия обнаружения улучшаются, так как при этом исчезнет или станет ничтожно малой составляющая сигнала (подставка) в опорном отсчете. При этом в опорном отсчете будет измеряться только шум, по значению которого оценивается значение шума в информационном отсчете, на основе чего устанавливается требуемый переменный порог для когерентного обнаружения в соответствии с выражением (12) и для некогерентного обнаружения в соответствии с выражением (26). При промежуточных фазовых соотношениях между навигационным и мешающим радиосигналами будут соответствующим образом перераспределяться значения вероятности правильного обнаружения в каналах обработки.

Заключение

В связи с повышением рабочих частот современных навигационных радиотехнических систем повышается интенсивность соответствующих мешающих отражений, поступающих в точку приема сигнала. Использование классических одноканальных схем оптимальной обработки сигналов в этих условиях приводит к существенным ошибкам в оценках параметров и координат объектов, а также к ошибкам при различении информационных символов.

В данной статье разработан способ и соответствующие модели комплексной (двухканальной) обработки навигационных сигналов, позволяющие значительно ослабить влияние мешающих отражений на основные характеристики их обнаружения без увеличения энергетических и частотно-временных ресурсов радиоканала. Получены выражения для инженерных расчетов основных вероятностных характеристик обнаружения сигнала для общего случая наличия в канале связи сигналов мешающих отражений и флюктуационного шума.

Полученные результаты могут быть использованы как при модернизации существующих, так и при создании перспективных навигационных радиотехнических систем, обладающих повышенной эффективностью функционирования в условиях сложной помеховой обстановки.

Исследование выполнено за счет гранта Российского научного фонда (проект № 16-1910089).