Модели контуров изображений объектов при наличии геометрических искажений

Геометрические искажения изображения возникают из-за изменения координат передаваемых элементов, проявляются в виде нарушения геометрического подобия воспроизводимого изображения и оригинала и оказывают значительное влияние на качество обработки и распознавание изображений объектов. При этом вначале определяются параметры геометрических преобразований, а затем по полученным параметрам осуществляется распознавание класса изображения [1].

В настоящее время предложены различные инварианты к аффинным преобразованиям, используемые при распознавании [2–6]. К таким инвариантам относятся, например, моменты разных порядков [2] или дескрипторы Фурье. При этом, как правило, рассматриваются изображения контуров и предлагаемые подходы к распознаванию базируются на сравнении двухмерных полей. Кроме того, в основном исследуется вопрос о влиянии линейных преобразований, таких как поворот, масштабирование и перенос на код контура и его спектр [7].

В том случае, когда необходимо оценить вид и параметры геометрических искажений, требуется набор эталонов для различных искажений. При этом математические модели для создания эталонов контуров искаженных изображений практически не представлены.

В работе [7] рассмотрен подход к обработке изображений объектов, основанный на обработке их контуров. Рассмотрение контуров изображений как комплекснозначных функций одной переменной и представление их в линейном комплекснозначном пространстве позволяет получить меру близости двух контуров в виде их скалярного произведения, инвариантную к линейным преобразованиям переноса, поворота и масштабирования.

Полигональный контур Г = { γ ( n )} 0, s –1 изображения объекта представляет собой периодическую последовательность элементарных векторов (ЭВ) γ ( n ), n =0, 1,…, s –1, где s – количество векторов в контуре. ЭВ при этом задаются в виде комплексных чисел: γ ( n ) = Re γ ( n ) + i Im γ ( n ).

В работе [7] рассмотрена группа линейных преобразований контура изображения объекта и их влияние на спектр контура. В частности, рассмотрены такие преобразования, как поворот контура, изменение масштаба и сдвиг начальной точки. Показано, что между кодами исходного Г и преобразованного путем поворота на угол ∆φ, растяжения в |µ| раз и сдвига начальной точки на d ЭВ Г(µd) контуров существует связь вида:

Г _µ ^{( d )} = {| µ |exp{ i ∆φ } γ ( n + d )}_{0, s - 1} .

Целью данной работы является разработка моделей контуров изображений объектов с геометрическими искажениями для формирования эталонов при решении задач оценки вида и параметров искажений.

1.    Геометрические искажения объектов простой формы

Под объектами с простой формой будем понимать объекты, спектр контура которых содержит только одну гармонику. К таким объектам относятся так называемые элементарные контуры, которые по своим спектральным свойствам являются аналогами синусоиды [7–9].

Рассмотрим следующие виды геометрических искажений: искажение типа «параллелограмм», изменение размеров изображения по вертикали и горизонтали, трапецеидальные искажения.

Элементарный контур (ЭК) Г m = { γ m ( n )} 0, s –1 порядка m , m =0, 1,…, s –1, задается как s -угольная ориентированная фигура с одинаковыми по модулю элементарными векторами, равными единице, и одинаковыми по величине углами между соседними ЭВ [7]:

„ f f 2 п 11

^Г m = ^{ Y m ⁽ n ^)} 0, s - 1 = ^ exP 1 i—mn [^ , I ^ ^ 0, s - 1

m = 0,1,..., s - 1.

Рассмотрим геометрическое искажение типа «параллелограмм». Для анализа возьмем контур Г = {4;– 4 i ;–4;4 i }. Элементарный контур Г является правильным четырехугольником и задает изображение квадрата. ДПФ Р Г = { ρ Г ( m )} 0,3 контура Г = { γ ( n )} 0,3 : ρ Г ( m ) = {0; 0; 0; 16} (рис. 1 а ).

На рис. 1 б показан контур N П ={ ν П ( n )} 0,3 и его амплитудный спектр, полученный из контура Г = { γ ( n )} 0,3 в результате геометрического искажения типа «параллелограмм».

о----о----о------- а)

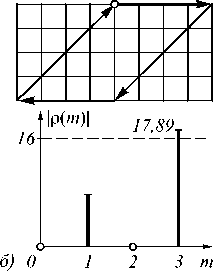
Рис. 1. Исходный контур Г и его амплитудный спектр (а)

и контур N П , полученный в результате геометрического

искажения типа «параллелограмм» (б)

Получена модель контура N n = { v n( n )} о,з :

v _n ( n ) = Y ( n ) + A sin I —3 n I , n = 0,1,..., 5 - 1,

где A – параметр геометрического искажения. Код полученного контура N П = {4; –4; –4 i ; –4; 4+4 i }. ДПФ

P n = { P n ( m )} о,з контура N n:

P _N ( m ) = p _Г ( m ) + iA p _{Im r} ( m ), m = 0,1,

...

, 5 — 1 ,

и равен p N ( m ) = {0; 8 i ; 0; 16–8 i }.

Таким образом, спектр контура в результате геометрического искажения типа «параллелограмм» изменяется. В его составе появляется дополнительная гармоника, которой не было в спектре исходного контура до преобразования. Кроме того, основная гармоника дополняется мнимой компонентой. Причем и дополнительная гармоника, и мнимая компонента основной гармоники имеют одинаковый уровень, зависящий от параметра A величины сдвига строк относительно друг друга при геометрическом искажении.

Исследовано влияние на контур геометрических искажений в виде изменения размеров изображения по вертикали и горизонтали. На рис. 2 показаны контуры, полученные из контура Г = { y ( n )} о,з в результате геометрических преобразований типа сжатие и растяжение по вертикали и горизонтали.

Получены математические модели контуров, подвергнутых геометрическим искажениям типа сжатие и растяжение по вертикали и горизонтали:

сжатие по вертикали:

I 2 п )

v СВ (n) = Y( n) — iA sin I —n I, k 5 )

растяжение по вертикали:

I ^{2 n} v РВ ( n ) = Y ( n ) + iA sin I — n k 5

сжатие по горизонтали:

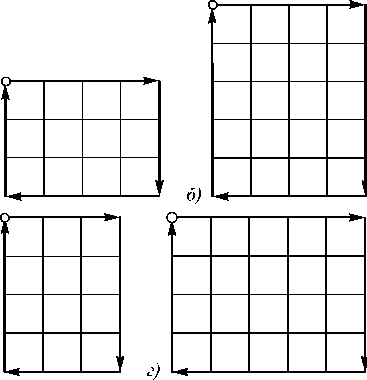
Рис. 2. Контуры, полученные в результате геометрических искажений в виде изменения размеров изображения: сжатие по вертикали (а); растяжение по вертикали (б); сжатие по горизонтали (в); растяжение по горизонтали (г)

ДПФ контуров, полученных в результате геометрических искажений в виде изменения размеров изображения, равно:

P СВ ( m ) = P г ( m ) — A P im Г ( m ),

P РВ ^{( m} ) = P r ^{( m} ) ^{+ A} P im Г ^{( m} ),

P СГ ( m ) = P r ( m ) — A P Re Г ( m ),

P _РГ ( m ) = P _r ( m ) + A P _{Re Г} ( m ), m = 0,1,..., 5 — 1.

Для контуров, представленных на рис. 2, получено:

P _СВ = {0;2;0;14}, P _РВ = {0; — 2;0;18},

P _СГ = {0; — 2;0;14}, P _РГ = {0;2;0;18}.

Таким образом, спектр контура в результате геометрического искажения в виде изменений размеров изображения также изменяется. В его составе также появляется дополнительная гармоника, которой не было в спектре исходного контура до преобразования. Однако по сравнению со случаем геометриче-

ского искажения типа «параллелограмм», дополнительная гармоника является вещественной. Кроме того, основная гармоника дополняется вещественной компонентой. Дополнительная гармоника и вещественная компонента основной гармоники имеют одинаковый уровень, зависящий от параметра A сте-

пени сжатия или растяжения.

Исследовано влияние на контур геометрического трапецеидального искажения. На рис. 3 показаны контуры, полученные из контура Г = { y ( n )} 0,з в ре-

зультате геометрического трапецеидального искажения в вертикальной и горизонтальной плоскостях.

Получены модели контуров, подвергнутых трапецеидальному искажению в горизонтальной плоскости:

v СГ ( n ) = y ( n ) — A cos

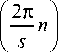
I 2п     | v ТГ (n) = y( n) + i A exp I i — 2 n I, n = 0,1,..., 5 — 1, k 5      )

растяжение по горизонтали:

и в вертикальной плоскости:

I ^{2 n} v РГ ( n ) = y ( n ) + A cos I — n k 5

Y ТВ ( n ) = Y ( n ) + A exp I i — 2 n I , n = 0,1,..., 5 — 1.

Для случая, изображенного на рис. 3, числовые значения контуров:

Г тг = {4 + i; - 5 i; - 4 + i ;3i}, гтв = {5;—1 — 4 i;—3;—1+4 i}.

ДПФ этих контуров:

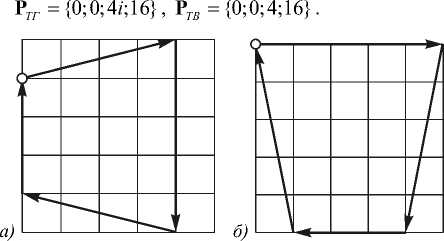
Рис. 3. Контуры, полученные в результате геометрического трапецеидального искажения: в горизонтальной плоскости (а); в вертикальной плоскости (б)

Получено, что к спектру исходного контура добавляется одна гармоника, уровень которой также определяется параметром A . В зависимости от того является эта гармоника вещественной или мнимой, определяется характер трапецеидального искажения. В том случае, если дополнительная компонента спектра мнимая, искажение в горизонтальной плоскости, а если компонента вещественная – искажение в вертикальной плоскости.

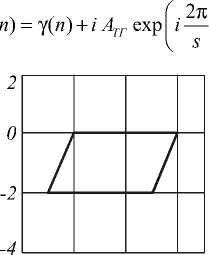
Одновременное воздействие разных искажений может быть представлено в виде суммы моделей отдельных искажений. Например, одновременные искажения типа «параллелограмм» и сжатие по вертикали могут быть представлены как (рис. 4 а ):

Г 2п ।            Г2n i v П СВ (n) = y(n) + АП sin I —3n I — i АСВ sin I —n I,

^,                            к 5      )             к 5 )

а одновременные искажения типа трапеция и сжатие по горизонтали (рис. 4 б ):

^v ТГ , СГ

0    2    4

Рис. 4. Контуры, полученные в результате одновременных искажений типа «параллелограмм» и сжатие по вертикали (а) и «трапеция» и сжатие по горизонтали (б)

а)

б)

2 n

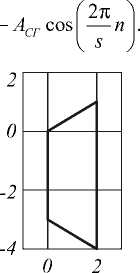
На рис. 5 а представлен анализируемый контур Г = {2; –2 i ; 2; –2 i ; –3; 2 i ; 2; 2 i }, а на рис. 5 б – контур N = {2; –2–2 i ; 2; –2–2 i ; –3; –3; 2+2 i ; 2; 2+2 i }, полученный в результате преобразования типа «параллело-

Рис. 5. Анализируемый контур (а) и контур, полученный в результате геометрического искажения типа «параллелограмм» (б)

ДПФ исходного контура Г : p Г ( m ) = {0; 2,297; –6,83; –0,464; –0,81; 8,854; 6,464; –5,88; 14,368}, и преобразованного контура: p N ( m ) = {0; 2,297+6,035 i ; –6,83+0,475 i ; –0,464+3,464 i ; –0,81+4,832 i ; 8,854–4,832 i ; 6,464–3,464 i ; –5,88–0,475 i ; 14,368–6,035 i }.

Спектр преобразованного контура дополнился мнимыми компонентами, и форма амплитудного спектра изменилась. Очевидно, что каждая гармоника спектра исходного анализируемого контура преобразовалась в соответствии с выражением (1). Получена модель преобразованного контура, записанная в виде ряда Фурье:

• 1    5 — ¹             Г2п    ^

v ( n ) = y ( n ) + A V p Г ( m )sin I — mn I =

• 5    m = 1             к 5      )

= y ( n ) + A Im Y ( n ).

В работе [7] показано, что произвольный замкнутый контур равен взвешенной сумме ЭК Г m , m = 1, 2,…, s –1:

5 — 1

^Г = V P ⁽ m ) ^Г m .

• 5 m = 0

Роль весовых коэффициентов играют элементарные векторы p ( m ) контура спектра разлагаемого контура Г . Таким образом, произвольный замкнутый контур из s ЭВ может быть разложен в базисе из полного семейства ЭК Г 1 , Г 2 ,…, Г s –1 , причем его координатами в пространстве C ^s будут ЭВ контура его спектра. Спектральный анализ контуров, осуществленный по правилам спектрального анализа обычных сигналов, позволяет решать задачи прохождения контуров через различные устройства обработки.

На рис. 6 представлены элементарные контуры, составляющие анализируемый контур, и их амплитудные спектры, а на рис. 7 – элементарные контуры, составляющие преобразованный контур, и их амплитудные спектры. При этом каждая гармоника спектра исходного анализируемого контура преобразовалась в соответствии с выражением (1).

Контуры, полученные путем суммирования ЭК, показанных на рис. 6 и 7, полностью совпадают с контурами на рис. 5.

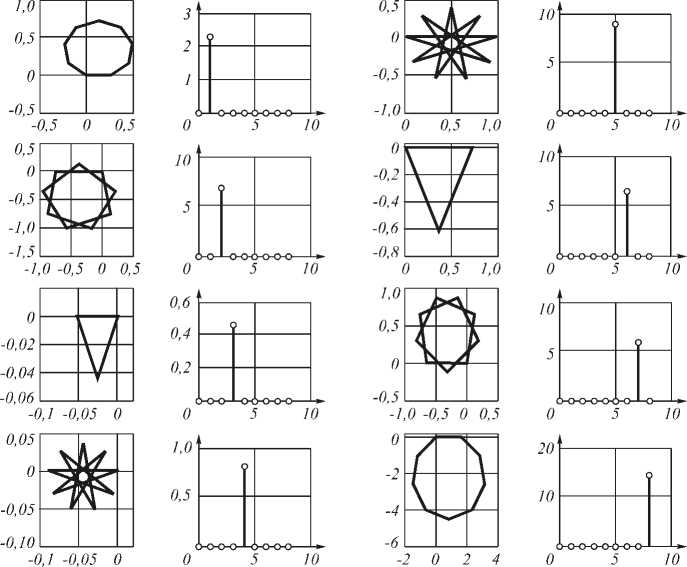
Рис. 6. Элементарные контуры, составляющие анализируемый контур, и их амплитудные спектры

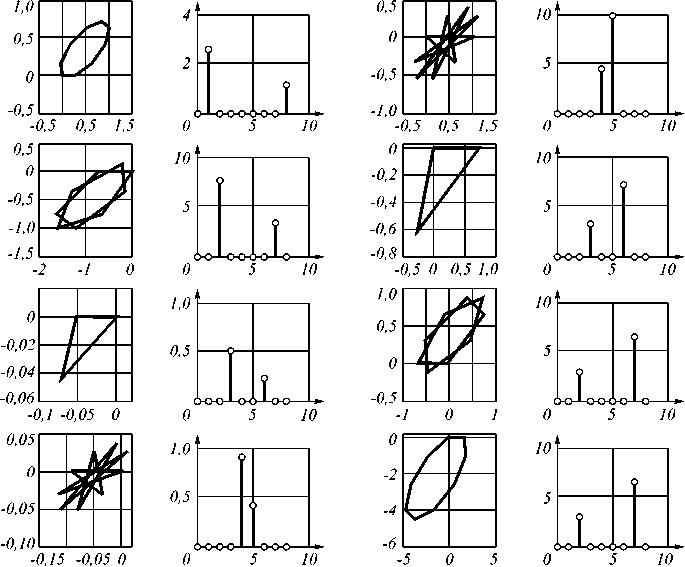
Рис. 7. Элементарные контуры, составляющие преобразованный контур, и их амплитудные спектры

Получены математические модели для контуров со сложным спектром, подвергнутых геометрическим искажениям типа сжатие и растяжение по вертикали и горизонтали:

сжатие по вертикали растяжение по вертикали

V РВ ( n ) = y ( n ) + A Z ^ ( m^ m = 0    s

. (2 n sin I — mn

I s

сжатие по горизонтали

^V СВ

V p(m) , ^2K

(n) = y( n)-iA / (-----sin I —mn m=0 s V s

, 0 <  A <  1 ,

s ^{- 1} p ( m )

^V СГ =Y ( ⁿ )^- A Z m = 0 s

( 2 n cos I — mn

V s

, 0 <  A <  1 ,

растяжение по горизонтали

V РГ ( n ) = Y ( n ) + A g B m m = 0    s

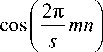
С учетом выражения для обратного дискретного преобразования Фурье:

V СВ ( n ) = y ( n ) - iA Im( Y ( n )),

^V рв ( ⁿ ) = y ( ⁿ ) + ^{iA Im(} Y ^{( n} )),

^V сг ^{( n} ) = Y ( ⁿ )^- A R^e( Y ^{( n} )),

^V рг ( ⁿ ) = Y ( ⁿ ) + A R^e( Y ^{( n} )).

На рис. 8 показаны результаты геометрических искажений типа сжатие и растяжение над контуром, представленным на рис. 5а

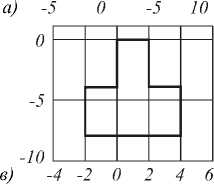
Рис. 8. Контуры, полученные в результате геометрического

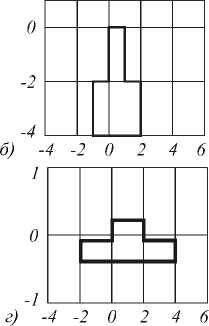
искажения типа сжатие и растяжение: растяжение по горизонтали (а), сжатие по горизонтали (б), растяжение по вертикали (в), сжатие по вертикали (г)

Структура спектров контуров произвольной формы, подвергнутых геометрическим искажениям типа сжатие и растяжение, определяется выражениями (2), так же, как и для простых контуров.

Таким образом, анализ спектров контуров искаженных объектов позволяет оценить вид и параметр геометрического искажения.

Контур изображения объекта представляется как одномерный сигнал и позволяет проще устранять эффекты геометрических искажений [2]. Однако существующие подходы основаны на обработке изображений контуров объектов и анализе двухмерных полей [2, 4]. Предложенные модели контуров являются одномерными функциями и позволяют достаточно просто получить любые комбинации искаженных контуров изображений объектов без использования трудоёмких матричных операций.

Заключение

Представлены математические модели контуров изображений объектов, подвергнутых геометрическим искажениям типа «параллелограмм», растяжение и сжатие по вертикали и горизонтали, а также трапецеидальному искажению. Показано, что в результате геометрического искажения спектр контура дополняется гармониками в зависимости от вида геометрического искажения. Получено, что одновременное воздействие разных геометрических искажений может быть представлено как сумма моделей отдельных искажений.

Предложенные модели искаженных контуров позволяют достаточно просто сформировать набор эталонов для различных искажений и их комбинаций.