Модели квантового глубокого машинного обучения: программно-алгоритмическая платформа квантового «Сильного» вычислительного ИИ
Автор: Боровинский В.В., Капков Р.Ю., Решетников А.Г., Тятюшкина О.Ю., Ульянов С.В., Решетников Г.П.
Журнал: Сетевое научное издание «Системный анализ в науке и образовании» @journal-sanse
Рубрика: Современные проблемы информатики и управления
Статья в выпуске: 1, 2025 года.
Бесплатный доступ
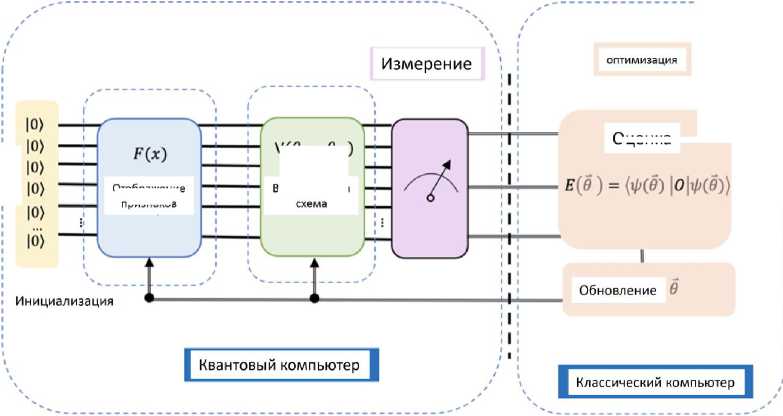
Рассмотрена цель машинного обучения состоит в том, чтобы обучить компьютер извлекать определенные свойства из заданного набора данных без явного кодирования или набора правил, а затем использовать полученные результаты для изучения этих свойств в новых данных в целях прогнозирования, классификации или построения модели исследуемого объекта. Обсуждаются наиболее популярные модели машинного обучения такие как контролируемое обучение (supervised learning) или обучение с учителем, при котором машина предварительно обучается с использованием некоторых помеченных данных. Другие формы обучения, такие как неконтролируемое и с подкреплением (unsupervised and reinforced), также широко изучались и применялись в различных областях. Тремя наиболее широко используемыми алгоритмами контролируемого машинного обучения, относящимися к квантовым вычислениям, являются (a) нейронная сеть (NN - neural networks) для синтеза квантовой логики, физического отображения и декодирования квантовых ошибок, протокол QKD (quantum key distribution), квантовый ускоритель ML, квантовые нейронные сети (QNN - quantum neural networks); (б) Обучение с подкреплением (RL) для декодирования квантовых ошибок и (в) Метод опорных векторов (или SVM - support vector machine) для квантового машинного обучения. В исследовании также обсуждаются различные модели обучения ML, включая метод случайного поиска для квантовой коммуникации. Работа рассчитана на повышение квалификации ИТ - специалистов, применяющих методы «сильного» ИИ.
Ускоритель для квантового машинного глубокого обучения, квантовая нейронная сеть, вариационные квантовые схемы, квантовое машинное обучение, алгоритм гровера
Короткий адрес: https://sciup.org/14133454
IDR: 14133454 | УДК: 512.6,
Текст научной статьи Модели квантового глубокого машинного обучения: программно-алгоритмическая платформа квантового «Сильного» вычислительного ИИ
Модели квантового глубокого машинного обучения: программно-алгоритмическая платформа квантового «сильного» вычислительного ИИ / В. В. Боровинский, Ю. Р. Капков, А.Г. Решетников [и.др.] // Системный анализ в науке и образовании: сетевое научное издание. 2025. № 1. С. 23-64. EDN: JJXGPN. URL:
Классические модели машинного обучения ( ML – machine learning ) как составляющая ИИ [1] применялись в различных областях квантовых вычислений [2-12], таких как квантовая коррекция ошибок, квантовая коммуникация, квантовая криптография, сопоставление квантовых алгоритмов с классическими алгоритмами в машинном обучении и т.д. С другой стороны, были разработаны квантовые аналоги существующих алгоритмов ML , такие как квантовая нейронная сеть ( QNN ), квантовый метод опорных векторов (или квантовая вспомогательная векторная машина – QSVM – quantum support machine ), которые, как ожидается, будут работать лучше, чем классические компьютеры, из-за экспоненциального увеличения пространства поиска. Более того, были разработаны квантово-классические гибридные алгоритмы [13 - 21], которые в некотором смысле имитируют принцип работы алгоритмов ML . Определялся глобальный оптимум для функции затрат, но для этого использовали квантовые компьютеры и обсуждался вопрос соотношения инженерии машинного обучения с квантовыми основами (математическое и концептуальное понимание квантовой теории в построении квантово-подобных, квантово-инспирированных, гибридных квантово-классических и т.п. моделей).
Цель машинного обучения состоит в том, чтобы обучить компьютер извлекать определенные свойства из заданного набора данных без явного кодирования или набора правил, а затем использовать полученные результаты для изучения этих свойств в новых данных в целях прогнозирования или классификации. Например, ожидается, что компьютер, который ранее видел большое количество изображений опухолей и был обучен распознавать злокачественные опухоли, сможет правильно идентифицировать невидимую фотографию опухоли. Этот тип алгоритма ML называется контролируемым обучением ( supervised learning ) или обучение с учителем, при котором машина предварительно обучается с использованием некоторых помеченных данных. Другие формы обучения, такие как неконтролируемое и с подкреплением ( unsupervised and reinforced ), также широко изучались и применялись в различных областях.
Тремя наиболее широко используемыми алгоритмами контролируемого машинного обучения, относящимися к квантовым вычислениям, являются ( a ) Нейронная сеть ( NN – neural networks ) для синтеза квантовой логики, физического отображения и декодирования квантовых ошибок, протокол QKD ( quantum key distribution ), квантовый ускоритель ML , квантовые нейронные сети ( QNN - quantum neural networks ); (б) Обучение с подкреплением ( RL ) для декодирования квантовых ошибок и (в)
Метод опорных векторов (или SVM - support vector machine ) для квантового машинного обучения. В исследовании также обсуждаются различные модели обучения ML [22-27], включая метод случайного поиска для квантовой коммуникации [11,12].
Примечание . Напомним, что однослойная нейронная сеть, построенная на методе обратного распространения ошибки аппроксимации и прямого действия исследуемой функции (сеть FFNN - feed - forward neural network ) состоит из входного слоя нейронов и выходного слоя нейронов. Задачей нейронной сети является аппроксимация функции с заданной точностью и минимальной потерей информации, содержащейся в исходной функции. В структуре многослойной сети с прямой связью первый уровень является входным уровнем, который принимает входной сигнал, а последний уровень является выходным уровнем. Между этими двумя слоями могут быть несколько скрытых слоев. Сигнал от входного слоя проходит через эти скрытые слои к выходному. Связь между парой узлов (нейронами) в двух соседних слоях имеет соответствующий вес, который указывает на силу связи между ними. Входные данные для определенного слоя умножаются на вес, чтобы получить внутреннее значение, которое изменяется на пороговое значение перед передачей в функцию активации для получения выходных данных этого слоя. Эти выходные данные передаются следующему слою в качестве входных данных. Конечный уровень предоставляет результаты работы сети. На каждой итерации веса и пороговые значения обновляются для получения более точного значения.
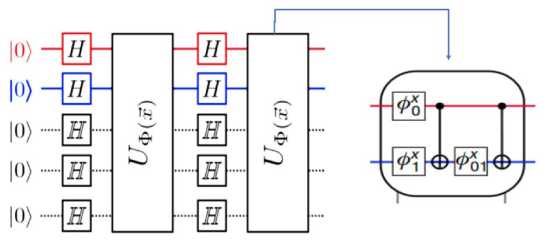
Функция потерь должна непосредственно содержать меру расстояния. Однако ее вычисление требует больших вычислительных затрат даже при использовании квантового компьютера. Поэтому используют неявную функцию потерь, полученную из показателя точности, который выражается как
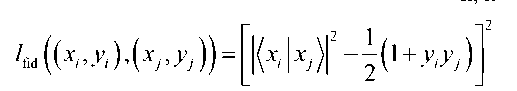
l fid ( ( x,, y ) • ( x j , У ,
)
Эта потеря точности может быть эффективно вычислена с помощью теста SWAP или прямого измерения перекрытия состояний (см. рис. 1).
NQE ( Neural Quantum Embedding) - эффективный метод, который использует возможности классических нейронных сетей для обучения оптимальному квантовому встраиванию для данной задачи. NQE может повысить разделимость квантовых данных, превосходящую возможности квантовых каналов, тем самым расширяя фундаментальные пределы квантового обучения под наблюдением. Подход позволяет избежать критических проблем, присущих существующим методам, таких как увеличение числа вентилей и глубины квантовой схемы, а также риск возникновения «бесплодных плато». Численное моделирование и эксперименты с устройствами IBM подтверждают эффективность NQE в повышении производительности QML по нескольким ключевым показателям машинного обучения. Эти улучшения распространяются на точность обучения, способность к обобщению, обучаемость и устойчивость к шуму, превосходя возможности существующих методов квантового встраивания.
Экспериментальные результаты демонстрируют эффективность NQE в совершенствовании алгоритмов QML [28]. Эксперимент состоит из трех основных этапов: применение NQE , обучение QCNN ( quantum convolution neural networks ) с использованием моделей NQE и без них и оценка точности классификации для обученной квантовой сверточной нейронной сети QCNN с использованием моделей NQE и без них. Унитарное преобразование, которое отображает x в квантовое пространство признаков, определяется выходными данными классической нейронной сети, обозначаемыми как g ( xt , w ) , где w представляет обучаемые параметры. Результирующее квантовое состояние имеет вид: | x ;. ( w )^ = V ( g ( xi , w ))| 0^ . Цель обучения - создать функции отображения, которые могут разделить два класса данных на два ортогональных подпространства. Эффективный расчет точности между двумя квантовыми состояниями, полученными с помощью отображения характеристик объектов, выполняется с помощью квантового компьютера.
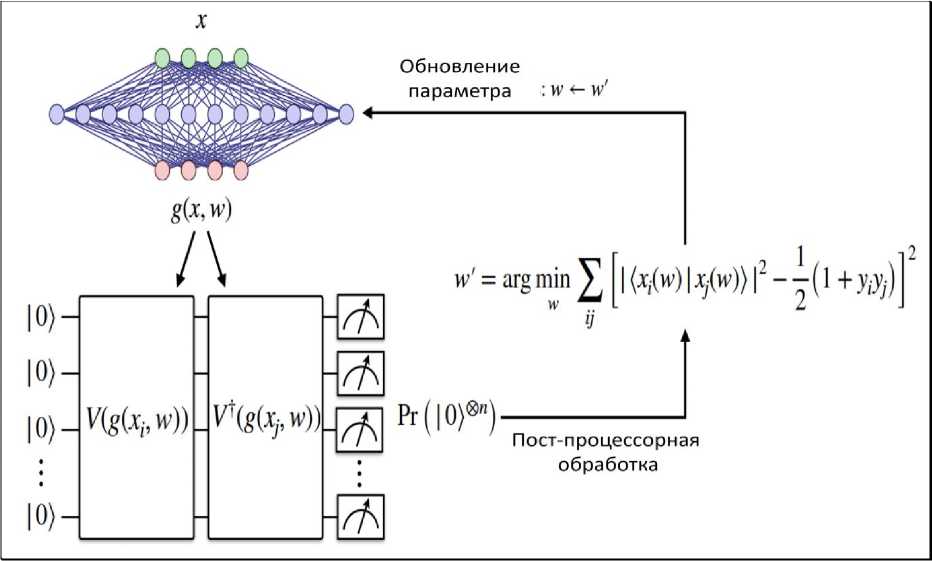
Рис. 1. Схема обучения NQE (Neural Quantum Embedding)
Схематическое изображение квантовой схемы, использованной в экспериментах, приведена на рис. 2.
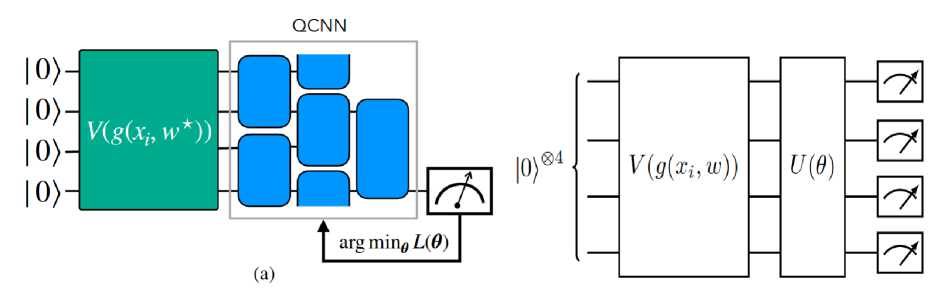
(а)
(б)
Рис. 2. (а) Схематическое изображение квантовой схемы, использованной в экспериментах. Зеленая секция указывает на нейронное квантовое встраивание (NQE), которое преобразует классические
данные xi в квантовое состояние
xi . Синяя часть представляет архитектуру квантовой сверточной нейронной сети (QCNN); (б) Квантовая схема, используемая для оценки локальной эффективной размерности. Отображение характеристик объекта, обозначенное как V ( g ( xi, w)), воздействует на начальное состояние 10^ для кодирования входного вектора xi. Затем для изменения состояния применяется параметризованное унитарное преобразование U (0), при этом параметры выбираются таким образом, чтобы минимизировать конкретную функцию потерь.
На рис. 3 приведен пример гибридной квантово-классической модели ML .
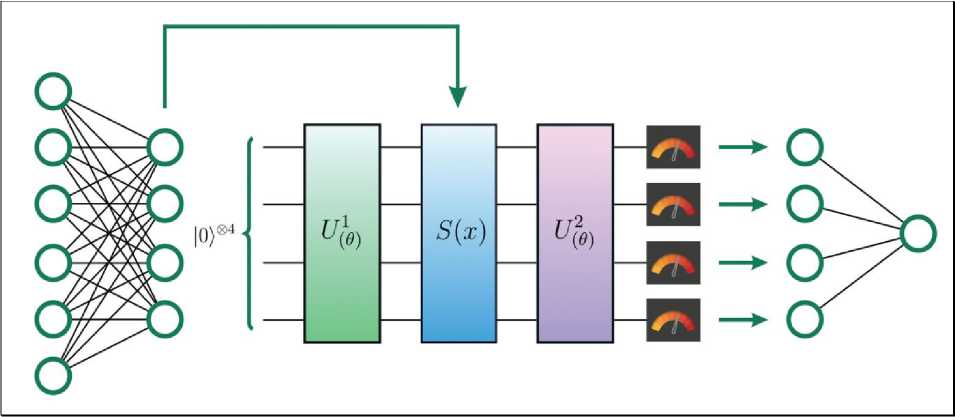
Рис. 3. Пример гибридной квантово-классической модели ML
В этом случае входные данные передаются в полностью подключенный классический многослойный персептрон, а его выходные данные подаются на встраивание квантовой схемы. В зависимости от настройки выполняются некоторые измерения этой квантовой схемы, которые затем передаются на другой полностью подключенный уровень, выходные данные которого можно сравнить с меткой.
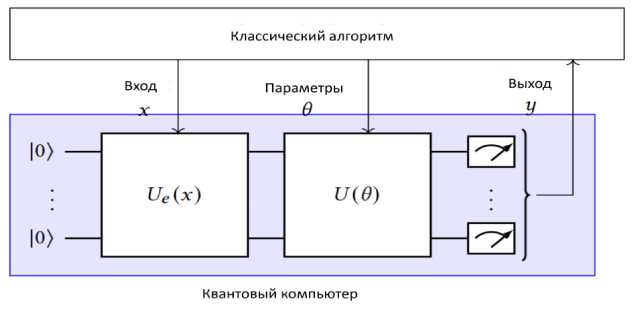
Междисциплинарная область QML находится на стыке ML и квантовых вычислений. Она охватывает несколько направлений исследований, в которых рассматриваются данные и алгоритмы, которые могут быть классическими, квантовыми или их гибридной комбинацией. Сосредоточимся на квантово-усовершенствованном ML , в котором рассматривается использование квантовых алгоритмов для улучшения задач ML для классических данных. Обычно это достигается с помощью гибридных алгоритмов, которые включают классическую и квантовую части. Такого рода алгоритмы уже могут быть запущены на современных устройствах NISQ .
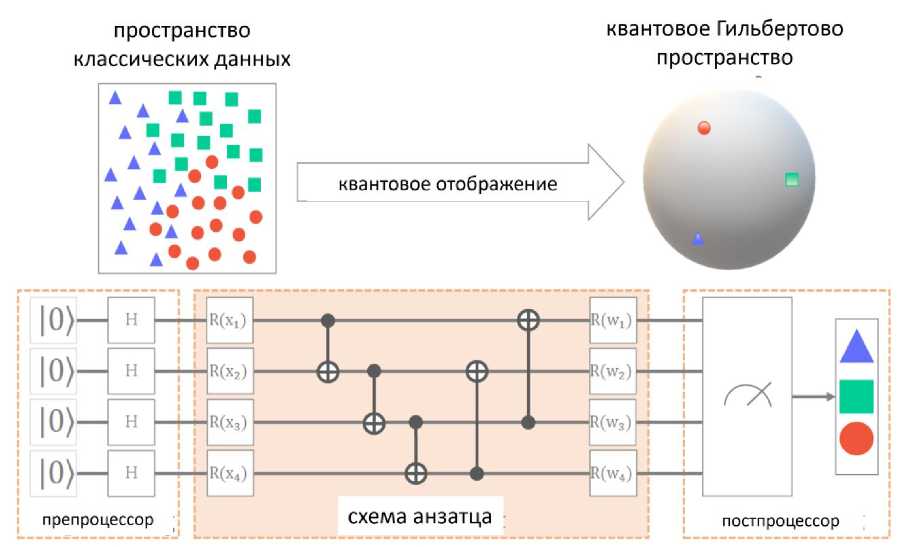
Структура квантового встраивания включает в себя множество схем-аналогов (рис. 4), что приводит к неразрешимым скрытым представлениям для универсальных квантовых вычислений. На рис. 4 показан упрощенный вариант такого гибридного ML -конвейера [29].
Подобно методам ядра, квантовое вложение преобразует наблюдения в классическом пространстве данных в квантовое гильбертово пространство квантовых состояний, которое может быть представлено внутренним произведением квантовых представлений. Представлена архитектура модели квантового машинного обучения, сформированной из выбранного набора квантовых схем. Схема - анзатц играет решающую роль в модели схемы, обеспечивая веса модели обучения w в соответствии с входными данными x .
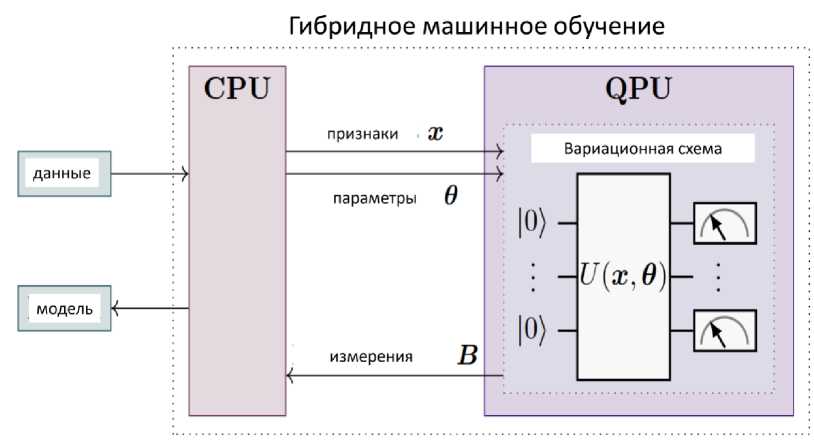
Классические данные передаются на классический головной процессор (обычно состоящий из (или более) центральных процессоров ( CPU ), графических процессоров ( GPU ) и оперативной памяти ( RAM )), который взаимодействует с QPU . На QPU выполняется квантовая схема. Эта схема управляется функциями и вариационными параметрами классического головного процессора. Признаки в этом контексте относятся к соответствующим образом предварительно обработанным классическим точкам данных, которые могут быть закодированы в схеме с помощью подходящей комбинации элементов таким образом, что результирующее квантовое состояние содержит соответствующую информацию, например, в виде амплитуд или углов.
Предварительно обработанные функции x и параметры классического процессора (представленные здесь центральным процессором) управляют вариационной схемой, которая выполняется на QPU . Результаты измерений B возвращаются на классический процессор и позволяют выполнить квантово-классическую оптимизацию параметров. В конечном итоге может быть реализована подходящая модель для предложенной задачи ML . В перспективе такой конвейер включает в себя несколько процессоров и QPU , а также графические процессоры.
(а)
(б)
Рис. 4. (а) Упрощенный эскиз гибридного конвейера ML в виде вариационного квантового алгоритма;
(б) Квантовые вложения для контролируемого квантового машинного обучения
Пример . В машинном обучении значения Шепли используют теорию игр для определения точного вклада каждого игрока. Кроме того, метод Шепли объясняет прогнозы, сделанные с помощью нелинейных моделей. В Python функции значений Шепли используются для интерпретации моделей машинного обучения. Значения Шепли ( SV ), которые представляют собой хорошо известный не зависящий от модели инструмент в классическом ML для оценки важности каждой характеристики для прогнозирования модели. В частности, предлагается применять SV для квантовых вентилей, которые являются строительными блоками моделей QML на квантовых компьютерах на основе вентилей. Называется такой подход квантовым Значением Шепли ( QSV ).
На рис. 5 приведены два подхода [30] для SVS в QML .
В обоих случаях функция значения, определяется результатами измерений. Показана примерная вариационная схема с четырьмя кубитами, состоящая из блока кодирования данных для k-мерного вектора признаков x и набора из пяти параметризованных элементов, как показано на рис.5, где каждый параметризованный элемент зависит от вектора параметров.
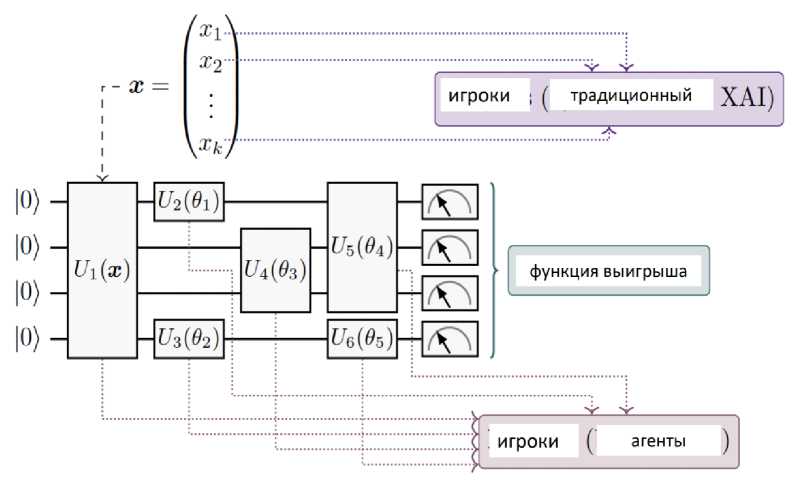
Рис. 5. Два возможных подхода к SV в QML, использующих вариационные квантовые схемы: (а) SV из классического ML, для которых объекты представляют игроков; (б) предложенные QSV, для которых квантовые элементы представляют игроков
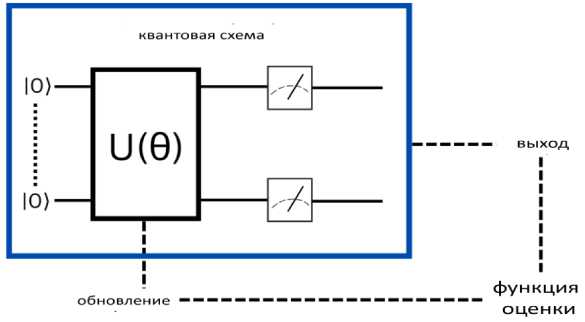
Квантовые нейронные сети ( QNN ) - подкласс вариационных квантовых алгоритмов, состоящий из квантовых схем, которые содержат параметризованные логические операции. Информация сначала кодируется в квантовое состояние с помощью процедуры подготовки состояния или отображения свойств. Выбор отображения свойств обычно направлен на повышение производительности квантовой модели и, как правило, не оптимизируется и не обучается. Как только данные кодируются в квантовое состояние, применяется вариационная модель, содержащая параметризованные элементы управления, которая оптимизируется для конкретной задачи. Это происходит за счет минимизации функции потерь, когда выходные данные квантовой модели могут быть извлечены из классической функции пост-обработки, которая применяется к результату измерения. Применяемая модель изображена на рис. 6.
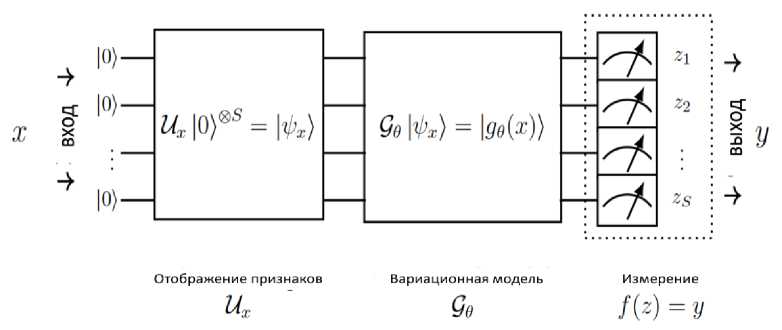
Рис .6. Модель квантовой нейронной сети [21]
Входные данные кодируются в гильбертово пространство S-кубита путем применения отображения свойств |^ := Ux |0)^S. Затем сформированное состояние преобразуется с помощью вариационной формы g (x)^ := G ^х^, где параметры 6 Е 0 выбираются таким образом, чтобы минимизировать определенную функцию потерь. Наконец, выполняется измерение z = (z1,...,zs) ,
минимизировать определенную функцию потерь. Наконец, выполняется измерение z = ( zr ,..., zs ) , результаты которого подвергаются последующей обработке для извлечения выходных данных модели y : = f ( z ) .
Классические данные x е □ s in кодируются в гильбертово пространство S -кубита, используя отображение свойств U . Сначала к каждому кубиту применяются гейты Адамара. Затем нормированные значения отображенных данных кодируются с помощью R Z -гейтов с углами поворота, равными значениям отображенных данных. Затем это сопровождается R ZZ -гейтами, которые кодируют данные более высокого порядка, т.е. контролируемые значения поворота зависят от произведения значений признаков отображенных данных. Затем повторяются применения R Z и R ZZ -гейтов. Как только данные закодированы, модель оптимизирует вариационную схему G^, содержащую параметризованные логические R Y - гейты с CNOT - слоями, формируя запутанные состояния между каждой парой кубитов, где 6 Е 0 обозначает обучаемые параметры.
На этапе пост-обработки измеряются все кубиты в базисе a z и классическим образом вычисляется четность выходных битовых строк. Для простоты рассмотрим бинарную классификацию, где вероятность наблюдения класса 0 соответствует вероятности наблюдения четной четности, и аналогично, для класса 1 с нечетной четностью. Выбор этой архитектуры модели обусловлен двумя причинами: отображение свойств служит полезной стратегией внедрения данных, которую, как считается, трудно смоделировать классическим способом по мере увеличения глубины и ширины массива, что значительно увеличивает мощность модели; и вариативная форма направлена на создание более выразительной схемы для квантовых алгоритмов.
1. Методы квантового глубокого обучения.
Рассмотрим некоторые распространенные методы квантового глубокого обучения [6-12].
-
А . Метод опорных векторов
Метод опорных векторов ( SVM - Support Vector Machine ) - алгоритм классификации с контролируемым машинным обучением, который создает разделяющую гиперплоскость для классификации. SVM обычно используется для бинарной классификации, и в этом разделе часто будем ссылаться на две бинарные метки в {0,1}. Цель применения SVM , состоит в том, чтобы максимально увеличить резерв. Сам резерв определяется как расстояние между разделяющей гиперплоскостью и обучающими выборками (как из 0, так и из 1 экземпляров), которые находятся ближе всего к этой гиперплоскости.
Ключевой идеей квантового SVM являются ядра, которые отличают ее от классических ядер SVM (таких как гауссовы или полиномиальные ядра). Функция квантового отображения признаков нелинейно преобразует классические точки данных, т. е. входные данные x , в нелинейное квантовое состояние, т.е. реализует отображение:
ф- xH ф(x)) ф(x )|
Далее создается отображение свойств объектов, математические свойства которых, с одной стороны, достаточно сложны, чтобы данные можно было легко разделить после их отображения, и в то же время достаточно просты, чтобы их можно было реализовать на реальном квантовом процессоре. Одно из возможных отображений свойств, которые используются в реализации, определяется с помощью унитарного:
Uф(x)= exp i £ ф (x)ПZi
^ S с [ 1, n ] i e S
где S e{0,1,...,n-1,(0,1),(0,2),...,(n-2,n-1)}, ф(x) = x{, ф(.,j)(x) = (n-xi)*(n — xj).
Примечание . Отображение ф представляет собой отображение классического состояния в квантовое, тогда как каждое из отображений ф просто преобразует отдельные координаты; U^) это функция отображения объектов, определенная на n -кубитах, размерность которых экспоненциально зависит от размера данных и номера кубита, генерируемая унитарным отображением: U^ = U^H 0 nU^H 0 n , которое преобразует классические входные данные X в квантовое состояние. Более конкретно, чтобы реализовать отображение ф , применяется отображение U^ к фиксированному квантовому состоянию. Таким образом, точки данных встроены в единое унитарное отображение Uf^, а не являются входным состоянием. Унитарную схему U^ часто называют “отображением свойств объектов”. Унитарная схема U^ строится путем повторения применения блока U^H 0 n , и этот блок повторяется d = 2 раза ( d - это глубина блока U^H 0 nU^H 0 n в схеме). Однако для создания более сложных и глубоких отображений признаков это количество может быть увеличено. Таким образом, параметры ( d,ф ( x ) ) можно настраивать для алгоритма классификации. Схема на рис. 7 для отображения объектов состоит из двух этапов, которые повторяются два раза ( d = 2).
(а)
(б)
Рис. 7. Схема отображения свойств
Сначала ко всем кубитам применяются гейты Адамара, затем диагональный элемент, который зависит от данных. Одна из идей, лежащих в основе этих отображений, заключается в необходимости кодировать данные таким образом, чтобы классические алгоритмы не могли имитировать их, что дает возможность получить преимущество перед классическими подходами. Отображение U^ для случая с двумя кубитами имеет простую форму (см. рис. 7(б)), где гейты - просто вращения, следующие этому правилу:
фi(x)=xi, ф(i,j)(x)=п-xi)^(n-xj)
Наконец, классический ввод данных загружается путем применения унитарной функции к исходному квантовому состоянию |0) 0 : | ф ( x )^ = U^ j0^ . В зависимости от графа связности квантового устройства квантовое отображение признаков имеет около -^—^ ( n обозначает количество кубитов) дополнительных параметров, которые могут быть использованы для кодирования большего количества данных. После отображения объекта к его состоянию применяется квантовая схема малой глубины. Затем выходные данные обрабатываются с помощью нескольких уровней параметрических гейтов путем настройки параметров (весовых коэффициентов).
Б . Вариационная схема для вариационных алгоритмов
Общий квантовый классификатор будет состоять из двух взаимосвязанных схем. Первая - схема “отображения свойств объектов”, которую обсуждали выше. Вторая, в сочетании с измерением, реализует гиперплоскостную классификацию в пространствах свойств объектов. Параметрами этого второго контура являются параметры обучения рассматриваемой модели. Этот второй контур является вариационным контуром, также называемым квантовым контуром малой глубины W(0). Вариационная схема - гибридная квантово-классическая схема, состоящая из параметризованных гейтов, зависящих от набора параметров 0 , а также алгоритма обучения и целевой функции.
В рассматриваемом случае обучим схему правильно обозначать точки данных. Если использовать некоторые параметры схемы для ввода входных данных в схему и вычисления результатов (выходы), то можем видеть, что вариационная схема обладает такой же интуитивностью, как и другие модели с улучшенным обучением. Вариационные схемы используются для различных краткосрочных применений, таких как оптимизация и в контексте машинного обучения [31]. Вариационные квантовые схемы обладают универсальными свойствами и уже показали положительные результаты в реальных тестах, но их природа сильно отличается. В целом они основаны на подходе, показанном на рис. 8.
(а)
(б)
Рис. 8. (а) Гибридный алгоритм, использующий VQC; (б) Представление схемы оптимизации вариационной квантовой схемы
VQC всегда состоит из трех частей. Первая часть - уровень кодирования, который переводит классические данные в квантовое состояние, применяя унитарный оператор Ue ( x ) в зависимости от данных. Вторая часть - вычислительный уровень, который преобразует квантовое состояние путем применения унитарного оператора U ( 0 ) в зависимости от параметров 0 . Заключительная часть -уровень измерений, который получает классические данные из квантового состояния. Классический алгоритм взаимодействует со схемой, передавая входные данные x в качестве параметров на уровень кодирования, передавая параметры 0 на уровни расчета и получая выходные данные от уровня измерения (рис. 8 (а)).
Аналог представляет собой миниатюрную схему, состоящую из множества элементов, имеющих регулируемые характеристики, включая угол наклона элемента, который управляет поворотом. Затем измеряется результирующее квантовое состояние, которое должно дать правильные ответы на поставленную задачу (классификация, регрессия). Этот процесс повторяется до тех пор, пока схема не даст приемлемых результатов.
При выполнении VQC необходимо оценить градиенты такой функции затрат относительно каждого параметра. В обычных нейронных сетях это обычно достигается путем обратного распространения между аналитическими процедурами. При использовании VQC процессы становятся чрезмерно сложными, и не можем достичь промежуточных квантовых состояний, если сначала не измерим их. В настоящее время усовершенствованный подход называется правилом сдвига параметров и требует применения схемы дважды для каждого параметра и измерения ее результата дважды. В отличие от этого, традиционное глубокое обучение требует всего лишь одного прямого и обратного прохождения по сети, чтобы собрать все тысячи градиентов. Правило сдвига параметров может быть распараллелено на нескольких симуляторах или квантовых устройствах. Однако это может оказаться непрактичным при большом количестве параметров.
2. Квантовый ускоритель для машинного глубокого обучения
За последние десятилетия был достигнут значительный прогресс в исследованиях ускорения нейронных сетей на классических процессорах, например CPU , GPU , ASIC, FPGA . Но с увеличением масштаба приложения возникает узкое место, связанное с объемом памяти, известное как "стена памяти". Именно здесь в качестве решения могут быть использованы усовершенствованные квантовые вычисления. Разработка машинного обучения с использованием классического аппаратного ускорителя может осуществляться в два этапа:
-
- Разработка аппаратного обеспечения с учетом особенностей нейронной сети: ускорители глубоких нейронных сетей - DNN ( deep neural networks ) на базе ПЛИС, оптимальный по стоимости дизайн на основе ПЛИС для сверточных нейронных сетей - CNN ( convolution neural networks ) с ограниченными временными рамками;
-
- Совместное проектирование нейронной сети и аппаратного ускорителя: интегрированная структура, выполняющая поиск адаптированных архитектур нейронных сетей, разработанных именно для безопасного вывода и способная напрямую изучать архитектуры для крупномасштабных целевых задач и целевой аппаратной платформы.
Для полного использования потенциала квантового компьютера необходимо выполнить совместное проектирование нейронной сети и квантовых схем. Система полного ускорения (см., рис. 9) состоит из трех блоков:
Классика Кванты Классика
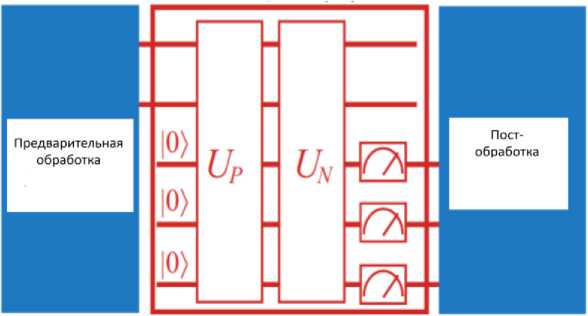
Рис. 9. Ускоритель квантовых вычислений
Предварительная и последующая обработка данных на классическом компьютере;
Ускоритель NN на квантовой схеме, включая подготовку квантового состояния ( U P );
Нейронные вычисления на основе QC ( U N ).
Отметим, что название "вариационный" отражает вариационный подход к изменению параметров. Вариационные схемы имеют хорошее сходство с нейронными сетями, которые имеют веса, которые нам необходимо оптимизировать, и на заре квантовых вычислений их называли квантовыми нейронными сетями. Вариационный алгоритм состоит из двух частей: этапа обучения и этапа классификации. Для обучения дается набор помеченных точек для выполнения обучения (см. рис. 10).
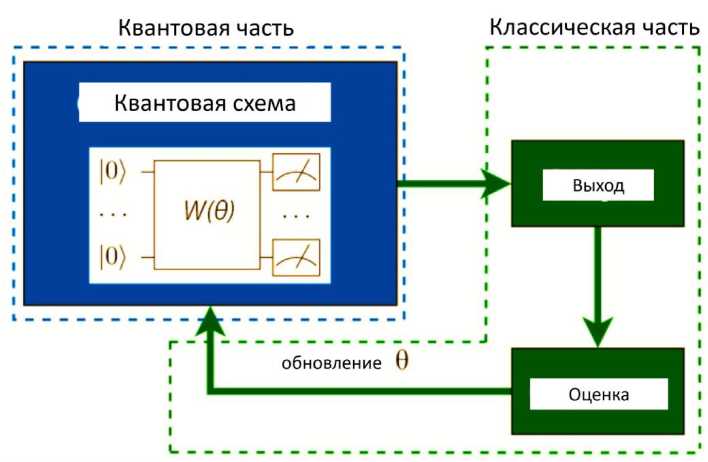
Рис. 10. Процесс создания вариационной схемы
Сначала мы обучаем классификатор, оптимизируя набор углов параметризации ( д ).
Задача - найти оптимальную схему классификации W ( д ) , которая разделяла бы наборы данных с разными метками. Для оптимизации нам необходимо определить функцию затрат, чтобы свести к минимуму вероятность присвоения решения неправильной метки. Ранее было объяснено, как работает квантовое отображение свойств признаков. Здесь рассмотрим схему отображения свойств признаков. Схема реализации показана на рис. 11.

Рис. 11. Схема реализации отображения свойств признаков
Напомним, что в квантовом классификаторе значения входных векторов преобразуются в параметры в унитарном виде. В примере на Рис. 11 использованы точки данных
= 1.5 ^
У Х 2
= 0.3 )
, которые
сгенерировали углы, как показано на рис. 11; H – гейт Адамара изначально применяется ко всем кубитам. Это позволяет подготовить равномерную суперпозицию всех битовых цепочек. За ним следует управляемый элемент управления U , который является управляемой версией однокубитного элемента управления U , и он полезен, поскольку позволяет применять квантовую фазу и определять ее с помощью:
U1 (^^ 0
0 "
ei ф у
. Кроме того, применяется многокубитный
элемент управления, который не контролируется. Напомним, что элемент controlled-NOT переключает цель, когда кубит находится в состоянии 1). Элемент Controlled- NOT определяется как таковой:
^ 1 0 00
0 100
0 0 01
ч 0 010
Цель ML -модели состоит в том, чтобы изучить функцию h ( x ), которая аппроксимирует исходную f(x ) с заданной точностью, при этом получая доступ к квантовому процессу E как можно реже (насколько это возможно) с небольшой средней ошибкой прогнозирования | h ( x ) — f ( x )| , усредненной по некоторому заданному распределению входных данных D ( x ) . Квантовая ML -модель обладает более широкими возможностями, чем классическая ML -модель.
На этапе прогнозирования классическая ML -модель ограничена обработкой классических данных, хотя и данных, полученных путем измерения квантовой системы на этапе обучения. В отличие от этого, квантовая ML может работать непосредственно в квантовой области. В некоторых задачах квантовая ML -модель обладает экспоненциальным преимуществом по сравнению с классической ML -моделью. Важный класс задач, связанных с квантовой механикой, заинтересован в прогнозировании функций вида f ( x ) = Tr ( OE (| x^x |) ) , где x - классические входные данные, E произвольное (возможно, неизвестное) полностью положительное отображение с сохранением следа ( CPTP ), а O - известная наблюдаемая величина. Эта модель охватывает физический процесс, который использует классические входные данные и выдает действительное число в качестве выходных данных. Таким образом, эта общая настройка также включает в себя изучение классических функций, таких как функции, генерируемые нейронными сетями. Она также охватывает многие классические задачи ML , такие как классификация и регрессия.
Отображение E характеризует (потенциально очень сложную) квантовую эволюцию, происходящую в лаборатории. В зависимости от параметра x определяется квантовое состояние E (| x^x |) . Наконец, в конце эксперимента экспериментатор измеряет определенное наблюдаемое значение O . Цель состоит в том, чтобы предсказать результаты измерений для новых физических экспериментов с другими значениями x , отличающимися от тех, которые были получены во время обучения.
Классические модели ML могут собирать классические данные измерений { ( o, , x ) } CC , где o i - результат, полученный при выполнении POVM -измерения состояния E (| x^x |) . Через N c обозначаем количество таких квантовых экспериментов, выполненных во время обучения в классической ML -среде. С другой стороны, мы рассматриваем квантовые ML -модели, в которых применение когерентно нескольких итераций CPTP -отображения E способно подготовить квантовое состояние, хранящегося в квантовой памяти, а предсказания производятся квантовым компьютером, имеющим доступ к этой квантовой памяти. Через N q обозначаем количество раз, которое использует E во время обучения в настройках процесса квантового ML .
Примечание . При сравнении не учитывается время работы классического или квантового компьютера, который генерирует прогнозы; интересует только то, сколько раз должен выполняться процесс E на этапе обучения в квантовых и классических условиях.
Пример. Рассмотрим задачу предсказания ожидаемых значений всех 4n наблюдаемых величин Паули в неизвестном квантовом состоянии n-кубита р с небольшой ошибкой предсказания в худшем случае. В этом случае используется функция f (x ) = Tr (OEp (Ixx)) = Tr (Pp), где
x e { I , X , Y , Z } , которая индексирует наблюдаемые значения по Паули и Е^ подготавливает неизвестное состояние p , а затем Px отображается в фиксированную наблюдаемую со значением O . Предсказание наблюдаемых величин Паули в среднем случае - гораздо более простая задача, поскольку большинство из 4 n ожидаемых значений экспоненциально малы по n .
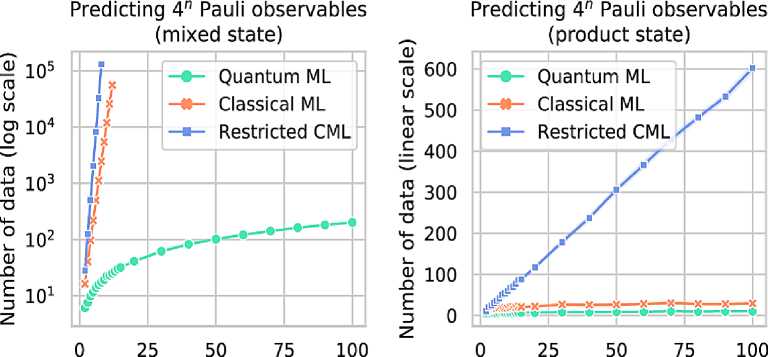
Численный эксперимент на рис. 12 отображает результаты наиболее известных процедур применения ML .
n (system size)
n (system size)
Рис. 12. Численные эксперименты – количество копий неизвестного состояния n-кубита, необходимое для прогнозирования ожидаемых значений всех 4n наблюдаемых Паули с постоянной ошибкой прогнозирования в наихудшем случае
Смешанные состояния: квантовые состояния вида ( I + P ) / 2 n , где P - наблюдаемый n -кубит Паули. Состояния произведений: тензорные произведения состояний стабилизатора с одним кубитом.
Таким образом, существует экспоненциальное различие между количеством копий состояния p , необходимым для классического и квантового ML для предсказания ожидаемых значений, когда оно находится в классе смешанных состояний. Однако для класса состояний от произведения это различие гораздо менее выражено. Ограниченный классический ML может получить результаты о г е { ± 1 } только с помощью Е [ ot ] = Tr ( P p )
Следовательно, каждая копия p предоставляет не более одного бита информации, и, следовательно, O ( п ) копий необходимы для прогнозирования ожидаемых значений всех 4 n, наблюдаемых по Паули. В отличие от этого, стандартный классический ML может выполнять произвольные измерения POVM для состояния p , поэтому каждая копия может предоставлять до n бит информации. Различие между классическим ML и квантовым ML является незначительным для состояний произведений.
Таким образом, точные результаты показывают, что классический ML , обученный с использованием данных квантовых измерений, может быть эффективным, укрепляя экспериментальные платформы, поддерживаемые классическим ML , и смогут плодотворно решать сложные квантовые задачи в физике, химии и материаловедении.
С другой стороны, строго установлен тот факт, что квантовый ML может иметь экспоненциальное преимущество перед классическим ML для определенных задач, где целью является достижение заданной ошибки прогнозирования в наихудшем случае. Важным направлением в будущем будет выявление дальнейших проблем в обучении, которые позволят получить существенные квантовые преимущества, указывая на потенциальные практические применения квантовой технологии.
При разработке новых моделей QNN или тестировании производительности QNN на заданном наборе данных важным шагом является эффективное моделирование динамики обучения QNN . На данном этапе создан ряд платформ для квантового моделирования.
QNN - модели, которые используются далее, включают QNN на основе амплитудного кодирования и QNN на основе блочного кодирования (см. рис. 13).
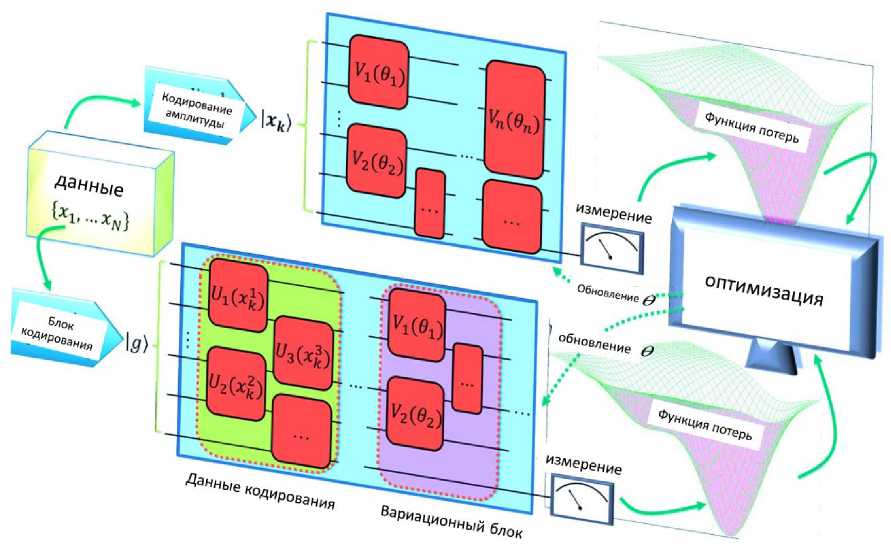
Рис. 13. Схематическая иллюстрация квантовых нейронных сетей (QNN) с двумя вариантами кодирования данных (двумя анзатцами): QNN на основе амплитудного кодирования и QNN на основе блочного кодирования [32]
Ожидаемые значения выходных состояний некоторых наблюдаемых величин часто используются в функции затрат для измерения расстояния между текущим и целевым прогнозами, в то время как классический оптимизатор используется для оптимизации параметров QNN для минимизации расстояния.
Более конкретно, QNN , основанные на амплитудном кодировании, обрабатывают данные, к которым есть прямой доступ. Например, если есть квантовая оперативная память для извлечения данных или данные поступают непосредственно из квантового процесса, можем предположить, что данные уже подготовлены в начале, и использовать вариационную схему для выполнения задачи обучения. В отличие от этого, QNN , основанные на блочном кодировании, обрабатывают данные, которые необходимо классически кодировать. Классическая стратегия кодирования может показаться неэффективной, но она более практична для экспериментальных демонстраций на устройствах NISQ по сравнению с QNN , основанными на амплитудном кодировании.
Благодаря успеху классического глубокого обучения, а также достижениям в области квантовых вычислений, квантовые нейронные сети ( QNN ), которые имеют сходство с классическими нейронными сетями и содержат вариационные параметры, привлекли большое внимание. Существует множество причин для разработки квантовой версии нейронных сетей.
Во-первых, квантовые компьютеры обладают потенциалом превосходить классические компьютеры по нескольким параметрам: некоторые алгоритмы, основанные на квантовом преобразовании Фурье, такие как алгоритм разложения на множители Шора, могут достигать экспоненциального ускорения по сравнению с наиболее известными классическими методами; Более того, доказано, что некоторые квантовые ресурсы, такие как квантовая нелокальность и контекстуальность, обеспечивают безусловные квантовые преимущества в решение определенных вычислительных задач.
Эти захватывающие результаты стимулируют изучение потенциальных преимуществ моделей QNN, особенно в эпоху больших данных.
Во-вторых, когда пытаемся извлечь уроки из квантового набора данных, то есть набора данных, данные которого генерируются в результате квантового процесса, а не из классического набора данных, было бы более естественно использовать квантовую модель для решения задачи: извлечения достаточного количества информации из квантового состояния в классическое устройство это было бы очень сложно при масштабировании системы, в то время как модель QNN , которая может обрабатывать данные в экспоненциально большом гильбертовом пространстве, естественно, может обеспечить определенные преимущества. Этот момент был явно продемонстрирован, когда модель QNN , может распознавать квантовые состояния одномерных топологических фаз, защищенных симметрией, лучше, чем существующие подходы.
В-третьих, с точки зрения эффективной размерности, которая является свойством, связанным с эффективностью обобщения модели на новых данных, имеются предварительные данные, свидетельствующие о том, что квантовые нейронные сети могут быть способны достичь лучшей эффективной размерности и более быстрого обучения, чем сопоставимые сети прямого действия.
Пример: Квантовая нейронная машина Борна (QNBM). QNBM - квантовый аналог классической нейронной сети с прямой связью. Каждому нейрону в сети присваивается кубит, и он подключается к предыдущему слою нейронов с помощью подпрограммы квантовых нейронов, которая представляет собой схему повторения до достижения успеха (RUS - Repeat - Until - Success). Подпрограмма «quantum neuron» (квантовый нейрон) состоит из входного регистра x , представляющего предыдущий уровень нейронов, выходного кубита, запущенного в состоянии ψout , представляющем нейрон следующего уровня, а также вспомогательного кубита, первоначально находящегося в 10а ^. Вспомогательный модуль используется для отображения функций активации от входного слоя нейронов | xin к каждому выходному нейрону | у out в следующем слое. Наглядное представление подпрограммы RUS для отдельного нейрона показано на рис. 14.
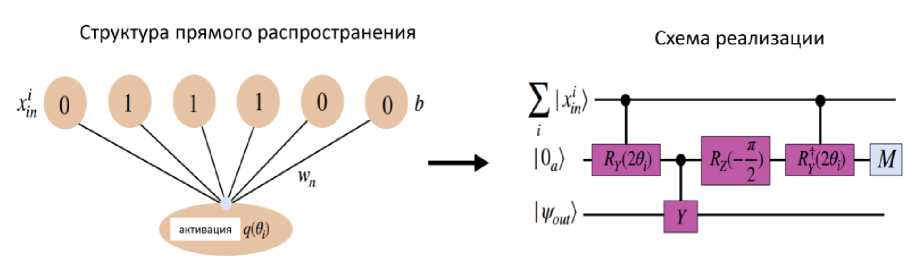
Рис. 14. Наглядная демонстрация отображения информации на один выходной нейрон в QNBM [33]
Слева показана структура обратной связи для активации нейрона, которая напоминает классическую сеть, содержащую обучаемые веса wn и смещения b для отдельных битовых цепочек. Функция активации q вносит нелинейность в выходной нейрон на следующем уровне. Справа показана реализация квантовой схемы, которая создает это нелинейное отображение в виде квантовой схемы RUS . Схема передает информацию из суперпозиции битовых цепочек на входном уровне ^ | х ;и ^ и выполняет нелинейную активацию на одном выходном нейроне | tyout ^. QNBM -просто многослойная сеть, состоящая из этих отдельных активаций квантовых нейронов. Основное различие между классической структурой (слева) и моделью квантовой схемы (справа) заключается в том, что квантовая сеть допускает суперпозицию входных данных на начальном слое.
Схема RUS выполняет нелинейную функцию активации для каждого выходного нейрона после суммирования весовых коэффициентов и смещений от нейронов предыдущего слоя. Конечное состояние каждого выходного нейрона при успешной активации может быть описано следующим образом: УF |х/и)®|0а) RRYq(2в)|Wout), где Fi - амплитудная деформация входного состояния во i время отображения RUS и вi сумма весовых коэффициентов и смещений для каждой входной последовательности битов. Из-за вращения RY общая функция, выполняемая на выходном узле, равна sin2 (q (2в)). Ключевым отличием QNBM от классических нейронных сетей является ее способность выполнять функцию активации на основе суперпозиции дискретных битовых цепочек
У
Основным строительным блоком QNBM является квантовая нейронная схема (показана на рис. 15), которая ранее была представлена в качестве потенциального строительного блока для QNN .
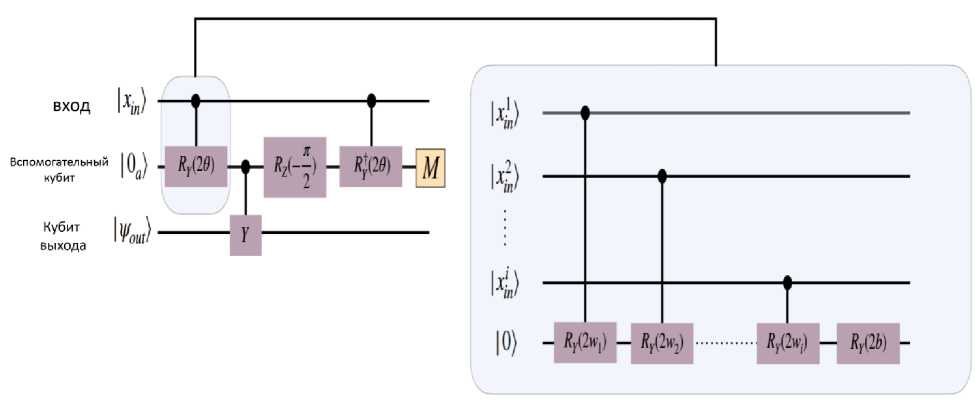
Рис. 15. Пример схемы квантового нейрона
Слева: Квантовая нейронная схема, соединяющая нейроны (кубиты) предыдущего слоя с одним нейроном следующего слоя. Если результат измерения вспомогательного элемента равен 0, схема R r ( 2 q ( в ) ) успешно применена к выходному кубиту, а если результат измерения равен 1, необходимо применить RY ( — п /2 ) к выходному кубиту, элемент NOT , для вспомогательного элемента и снова применить схему. Следовательно, схема квантового нейрона - схема повторения до достижения успеха. Справа: реализация RY ( 2в ) , где в - функция весов, смещений и входных значений нейрона.
Каждому нейрону в сети присвоен кубит, поэтому схема QN имеет входной регистр 1 т/, представляющий предыдущий слой, выходной кубит, инициализированный в состоянии |я(), представляющем нейрон следующего слоя, а также вспомогательный кубит, первоначально включенный в 10а ^. Предположим, что | xin изначально это одна строка битов, а не суперпозиция строк битов. Затем, непосредственно перед измерением (см. рис. 15 слева), объединенное квантовое состояние имеет вид:
I | = | х^ ®( ^^в)\ 0 а ) ® Rr ( 2 q ( в ) )| Y ou] + ^ 1 - Р ( в ) I1 . ) ® R y ( п /2 )1 W out ))
n где 0 - взвешенная сумма активаций нейронов на предыдущем слое: в = У wixi + b , wi ^ (—1;1)
i = 1
-
- веса, и b 6 ( — 1;1) - смещение. Аргумент поворота по оси у равен не 2 0 , а 2 q (0): это функция активации q ( в ) = arctan ( tan 2 ( в ) ) . Функция активации имеет сигмовидную форму и определяется
последовательностью применяемых квантовых гейтов. Пока для упрощения используем только эту функцию активации.
В любом случае, просто измерив 0
с вероятностью p ( 0 ) > —
наличия вспомогательного
кубита, получим правильную оценку состояния для следующего слоя:
I V = 1 x j ®| 0 .) ® R y ( 2 q ( 0 ))| P out}
•
Если вероятность 1 - p ( 0 ) > —,
то окажемся в состоянии:
I V =1 Х . ) ®| 1 J ® R y ( п /2 )| v j.
которое может быть возвращено в исходное состояние с помощью элемента NOT на вспомогательном устройстве и RY (—п /2) применено к выходному кубиту. Затем процесс будет повторяться до тех пор, пока вспомогательное измерение не даст результат 0a , таким образом, схема квантового нейрона относится к классу схем повторения до успешного завершения (RUS - Repeat Until Success)•
Важно отметить, что если мы позволим входному регистру находиться в общем состоянии - в виде суперпозиции битовых строк
Х|Х^, то схема успешно применит соответствующие преобразования к каждой из битовых строк в суперпозиции, что приведет к конечному состоянию: XF|4)®|0h®Ryq(20)|гЛ Здесь F относится к амплитудной деформации входного i состояния во время отображения RUS. Хотя эти базовые блоки QN ранее использовались для проектирования маломасштабных квантовых сетей для задач обучения с контролем, здесь можем модифицировать схему QN для генеративного моделирования. В частности, добавляем параметризованные нелинейные преобразования в структуру «Born Machine».
3. От квантового нейрона (QN) к квантовой нейронной машине Больцмана (QNBM)
До сих пор только показывали, как один нейрон в слое может быть связан со всеми нейронами в предыдущем слое. Кроме того, подключение слоя k к слою k - 1 в сети прямой связи является тривиальным расширением - можно повторить схему QN для каждого нейрона в слое k (как показано на рис. 16).
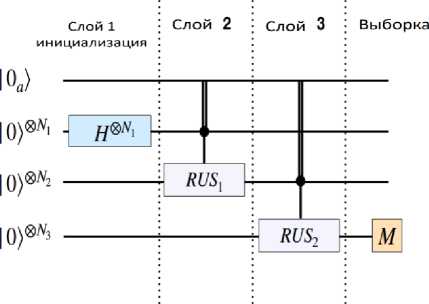
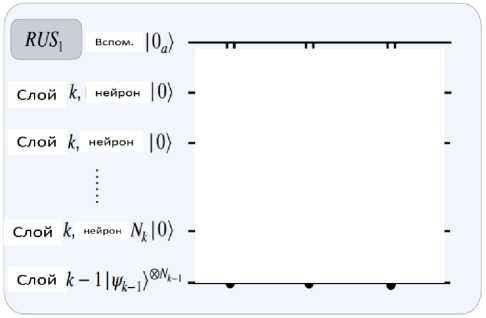
Рис. 16. Компонент квантовой схемы квантовой нейронной машины Борна слева: схема QNBM с 3 -мя слоями, где RUS 1 и RUS 2 представляют собой соединения между слоями
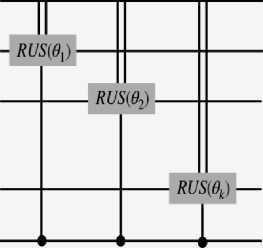
Входные нейроны инициализируются в однородной суперпозиции, а распределение вероятностей на выходе генерируется путем измерения выходного слоя. Справа: соединение двух слоев QNBM . Это равносильно запуску квантовых нейронных цепей RUS для каждого нейрона в слое k [34].
Ограничиваем эту работу значением k = 3, где количество нейронов во входном, скрытом и выходном слоях обозначается как ( N in , N hid , N out ) соответственно. Также кубит « ancilla » |0 а^ может быть повторно использован для каждой схемы RUS , поскольку после каждой схемы ancilla всегда включается и не коррелирует (отсоединяется) от всех нейронов. Таким образом, последующие измерения ancilla не влияют на уже подключенные нейроны. Аналогично, подключение всей сети сводится к повторению описанных выше действий для каждой пары соседних уровней.
Примечание . Предлагаемая здесь квантовая нейронная сеть не зависит от приложений и может, например, использоваться в классификации путем добавления встраивания данных и расчета затрат. Чтобы использовать ее в качестве генерирующей модели, вносим два изменения. Во-первых, квантовое состояние входного уровня инициализируем первый уровень в виде однородной суперпозиции битовых цепочек с помощью элементов Адамара, поскольку он способен вводить некоторую внутреннюю структуру в схему в качестве аналога классического предварительного распределения. Во-вторых, измеряем только кубиты, представляющие выходной слой, по аналогии с классическими нейронными сетями. Результирующее распределение вероятностей затем является результатом QNBM и оптимизируется точно так же, как и в QCBM , при этом веса и смещения выступают в качестве свободных параметров.
В квантовых вычислениях одной из наиболее сложных задач является моделирование гамильтониана. Моделирование гамильтониана - задача, для решения которой требуются алгоритмы, эффективно реализующие эволюцию квантового состояния. Ричард Фейнман предложил задачу моделирования гамильтониана в 1982 году, где он рассматривал квантовый компьютер в качестве возможного решения, поскольку моделирование общих гамильтонианов, по-видимому, растет экспоненциально относительно размера системы. В настоящее время эта проблема отражена практически во всех исследуемых системах, где хотим проанализировать физический дизайн и динамику в рамках вычислительной модели.
Задача гамильтонова моделирования определяется уравнением Шредингера, где оно дает эрмитову матрицу H (2 n х 2 n ), которая воздействует на n кубит за время t , и максимальную ошибку моделирования s , цель которой - найти алгоритм, который аппроксимирует оператор U таким образом, что || U -( e - iHt )|| < s , где e - iHt - идеальная эволюция. Квантовое моделирование динамического поведения системы обычно выполняется за полиномиальное время P, BQP и т.д. Но его гамильтонова матрица растет экспоненциально 2 n х2 n , что соответствует n кубитам исследуемых систем.
Таким образом, разрабатываются методы поиска наилучшего решения, допускающего ошибку. Существует две стратегии: «Юлий Цезарь» - («разделяй и властвуй» - « divide and conquer »); и алгоритм квантового блуждания. Вспомогательный элемент - локальный гамильтониан для некоторых конкретных гамильтонианов. K -локальный гамильтониан - эрмитова матрица, действующая на n кубитов, которая может быть представлена как сумма m членов гамильтониана, действующих не более чем на каждый из кубитов: H = ^. H . Это также приводит к d -разреженности. Говорят, что гамильтониан является d -разреженным (на фиксированной основе), если в любой строке или столбце содержится не более d ненулевых записей. Начиная с алгоритма "Разделяй и властвуй", первый шаг разбивает гамильтониан на сумму небольших и простых гамильтонианов, а второй шаг направлен на рекомбинацию сумм небольших и простых гамильтонианов.
Для этого есть три метода:
Первый метод - один из подходов, который представляет собой e i(A+B)t, где A и B - малые и простые гамильтонианы в приближении
(^,- iAt / r g- iBt / r ) r
для большого действительного значения r ;
Второй метод сочетает в себе линейную комбинацию унитарных преобразований ( LCU - Linear Combination of Unitaries ) и усиление амплитуды без запоминания ( OAA - Oblivious Amplitude Ampli fi cation ).
Новейшей технологией является квантовая обработка сигналов ( QSP - Quantum Signal Processing ).
Квантовое машинное обучение ( QML ) исследует взаимодействие и использует преимущества идей и технологий квантовых вычислений и машинного обучения. Таким образом, QML - гибридная система, включающая как классическую, так и квантовую обработку, в которой квантовым устройствам предоставляются сложные с точки зрения вычислений подпрограммы. QML пытается использовать преимущества классического машинного обучения, которое работает лучше всего, и его стоимость, например, вычисление расстояния (внутреннее произведение), передавая его на квантовый компьютер, который может изначально вычислить его в гильбертовом векторном пространстве. В эпоху больших объемов классических данных и небольшого количества кубитов наиболее распространенным применением является разработка алгоритмов машинного обучения для классического анализа данных, выполняемых на квантовом компьютере, т.е. машинного обучения с квантовым расширением.
Обычные контролируемые процессы обучения в QML можно определить следующим образом:
-
• Отображение квантовых характеристик: это подготовка данных. В литературе этот этап называется подготовкой состояния;
-
• Квантовая модель: это создание модели. В литературе это называется унитарной эволюцией;
-
• Классическое вычисление ошибки: это этап вычисления ошибки, на котором модель наилучшим образом аппроксимирует входной набор; в машинном обучении этот этап известен как прогнозирование;
-
• Наблюдаемые: обычно этот этап включается в вычисление ошибки. Наблюдаемое проявляется в виде линейных операторов в гильбертовом пространстве, представляющем пространство состояний квантовых состояний. Собственные значения наблюдаемой - действительные числа, соответствующие возможным значениям; динамическая переменная, определяемая наблюдаемой, может быть измерена. В качестве наблюдаемой используем операторы Паули. Тем не менее, можем использовать некоторую линейную комбинацию этих операторов или некоторую аппроксимацию от них для выполнения конкретных измерений.
В типовом представлении квантовой модели (см. рис. 17) отображение характеристик объектов обычно рассматривается как фиксированный единственный блок в начале квантовой схемы и без повторений.
Оценка
Отображение признаков
Рис. 17. Стандартная QML - модель только с одним встраиваемым блоком и анзатцем в виде параметризованной квантовой схемы с m параметрами
V(*>1 -«W
Вариационная
У этой модели есть ограничение: в худшем случае, когда входные данные не очень хорошо закодированы, для многих параметров, которые добавляем в параметрическую функцию/схему, не можем найти наилучшую модель, обобщающую входные данные.
Получаем классические данные, а квантовый компьютер обрабатывает их и возвращает результат после измерения. Существуют другие (три дополнительных) различных подхода и
Сетевое научное издание «Системный анализ в науке и образовании» Выпуск №1, 2025 год комбинации для обработки классических или квантовых данных с помощью гибридных вычислений. В методах QML для обработки классических данных выполняются некоторые фундаментальные операции, называемые встраиванием. Процесс встраивания описывается как классическое кодирование входных данных в квантовые состояния. Называем отображение характеристик объектов контейнером, выполняющим указанную операцию отображения (встраивания). Кодирование встраивания может быть амплитудным, фазовым, базовым или гамильтоновым, что является ключевым процессом работы QML в вариационных квантовых схемах для глубокого обучения с подкреплением.
4. Квантовое машинное обучение (QML) с использованием вариационных квантовых схем (VQC)
Исследования в области QML существует множество подходов. Ожидаемое преимущество QML в значительной степени зависит от доступа к гильбертову пространству высокой размерности, предоставляемого квантовыми системами. Здесь кратко обсудим подходы квантовых алгоритмов обучения с подкреплением ( QRL ), основанных на вариационных квантовых схемах ( VQC ). QML часто имеет дело с математическими ожиданиями квантовых измерений. Математическое ожидание наблюдаемой величины O относительно квантового состояния | ^ ^ обозначается как O О^ ^ := ^|O| ^ ) . В то время как VQC определяют новый класс ML -моделей, можно привести приблизительную аналогию с NN , где соотношение входных и выходных данных зависит от набора весовых коэффициентов.
Соответствующий гейт совершает поворот вокруг определенной оси на некоторый угол θ 0 . Множество гейтов вращением образуют квантовую схему, где θ суммирует все свободные параметры. Изменение этих значений дает возможность определить эволюцию квантовой системы. Пусть Uθ обозначает соответствующий унитарный элемент. Схематический пример VQC показан на рис. 18.
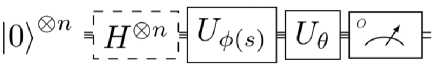
Рис. 18. Вариационная квантовая схема, состоящая из отображения характеристик объектов, вариационного слоя и измерения
Большинство задач RL используют концепцию состояний, на основе которых должно быть принято обоснованное решение. Эта информация о состоянии кодируется в квантовой системе с помощью соответствующего отображения характеристик. Как правило, входные данные s предварительно обрабатываются с помощью некоторой функции отображения Φ. Результаты Φ( s ) могут быть аккуратно интегрированы в квантовую схему с помощью единого унитарного преобразования U Φ( s ). Для повышения выразительности VQC можно использовать более сложные процедуры кодирования данных, такие как повторная загрузка данных или инкрементная загрузка данных. В конечном счете, некоторые наблюдаемые величины должны быть измерены. Обычно используется вычислительная база с O = Z ⊗ n .
В целом, выходные данные VQC -модели можно описать следующим образом:
{Os,. = (° I ( UU Xs ) ) ’ O U > U^ s ) I °) : = (° I O^OU ,^ °)
Для большинства задач это значение обрабатывается с помощью некоторой функции f . Сохраняя
максимально общий вид, можно определить функцию потерь L
для
f ( O ss , 9 ) (на
основе
конкретной задачи). Обновление параметров может быть выполнено, например, с использованием методов, основанных на градиенте: 0 ^ 0 + a-V9Lf ((O^ J • Требуемый градиент может быть получен с помощью правила сдвига параметров.
Общим является использование VQC в качестве аппроксиматора параметризованных функций. Типичный гибридный конвейер представлен на рис. 19.
Эта идея была впервые предложена для аппроксимации Q -функции и распространена на стратегию аппроксимации. QPU используется для аппроксимации соответствующей функции, в то время как предварительная и последующая обработка и оптимизация выполняются на классическом оборудовании. Взаимодействие с окружающей средой зависит от конкретного случая проблемы (например, классическая или квантовая среда).
Алгоритм следует понимать как гибридный, поскольку большая часть работы, особенно оптимизация, выполняется на классическом оборудовании. Агент наблюдает за текущим состоянием среды st, и применяет некоторую предварительную обработку ф. Результат кодируется с использованием отображения характеристик объектов U . С текущими вариационными параметрами θt подготавливается квантовое состояние и измеряется наблюдаемая Oa (потенциально зависящий от действия). Ожидаемое значение O может быть подвергнуто последующей обработке для представления, например, функции значения состояния-действия Qe (s, a) или стратегии п
(a\s). В зависимости от экземпляра агент использует эту функцию для выборки действия и выполняет его в среде.
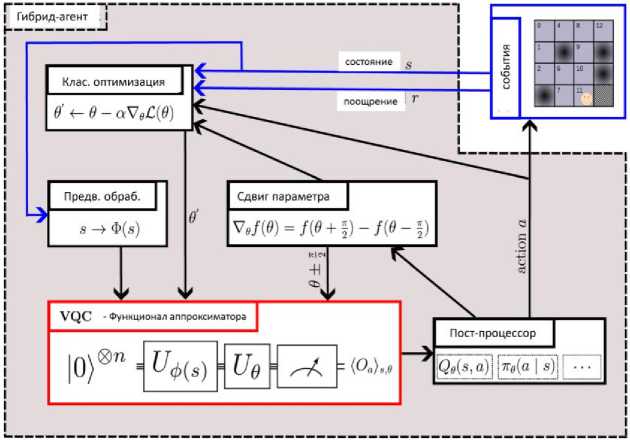
Рис. 19. Гибридный квантово-классический агент в типичном конвейере RL на основе VQC [35]
Вознаграждение r t (и, возможно, также последовательное состояние s t +1 ) отслеживается классическим оптимизатором. Чтобы включить обновление параметров на основе градиента, дополнительный гибридный модуль использует правило сдвига параметров для вычисления градиентов выходных данных VQC с учетом вариационных параметров θ t . Классический оптимизатор определяет новый набор параметров θt +1 и создает экземпляр VQC с этими обновленными параметрами. Эта общая итеративная процедура взаимодействия с окружающей средой, аппроксимации функций и обновления параметров повторяется в течение нескольких эпизодов точно так же, как, например, для DRL . Состояние RL интерпретируется как битовая строка, которая может быть закодирована с использованием идентичности Rz ( п ) Rx П )1 0 = 11 • Структура запутанности соединяет ближайших соседей с воротами CZ . Вариационные параметры учитываются при вращении отдельных кубитов вокруг осей x , y и z . Значение состояния-действия расшифровывается путем измерения наблюдаемых величин Паули- Z на нескольких кубитах, что соответствует количеству действий в окружающей среде. Полная схема VQC представлен на рис. 20.
Приближаясь к эпохе зашумленных квантовых вычислений промежуточного масштаба (NISQ), интересно исследовать, существует ли какой-либо квантовый алгоритм, который может не только решать фундаментальные проблемы обучения с обещанными квантовыми преимуществами, но и может быть эффективно реализован на квантовых устройствах. Для достижения этой цели одним из наиболее вероятных решений является квантовая нейронная сеть (QNN), которая также называется вариационными квантовыми алгоритмами [36,37]. Конкретно, QNN состоит из вариационной квантовой схемы для подготовки квантовых состояний и классического контроллера для выполнения задач оптимизации [38].
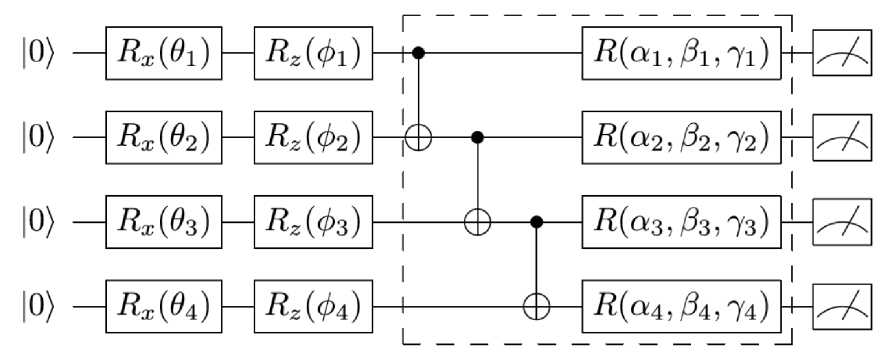
Рис. 20. Структура VQC
Элементы R и R используются для кодирования состояний. Несколько параметризованных уровней (пунктирная рамка) повторяются для формирования аппроксиматора Q -функции. Значения функции декодируются с использованием 1-кубитных наблюдаемых Паули- Z .
Частичным доказательством, подтверждающим это утверждение, является теоретический результат о том, что распределение вероятностей, генерируемое вариационной квантовой схемой, используемой в QNN , не может быть эффективно смоделировано классическими компьютерами. Учитывая высокую выразительность квантовых схем и схожую философию работы QNN и классической глубокой нейронной сети ( DNN ), вполне естественно использовать возможность реализации QNN на квантовых компьютерах в ближайшем будущем для выполнения определенных задач машинного обучения с более высокой производительностью по сравнению с классическими алгоритмами обучения.
5. Квантовое обучения квантовых нейронных сетей на основе поискового алгоритма Гровера
Конкретным примером достижения этой цели является квантовая нейронная сеть ( QNN ), которая была разработана для выполнения различных задач контролируемого обучения, таких как классификация и регрессия. Однако есть две основные проблемы, которые остаются неясными, когда QNN используется для выполнения задач классификации.
Во-первых , квантовый классификатор, который может эффективно сбалансировать вычислительные затраты, такие как количество измерений и эффективность обучения, остается неизученным. Во-вторых , неясно, могут ли квантовые классификаторы применяться для решения определенных задач, которые превосходят их классические аналоги. Здесь рассмотрим схему квантового обучения на основе поискового алгоритма Гровера ( GBLS - Grover - search based learning scheme ) для решения вышеуказанных проблем. Центральной концепцией GBLS является переформулировка задач классификации в задачу квантового поиска.
Хотя преимущество квантового алгоритма поиска по методу Гровера очевидно, способ преобразования задачи классификации в задачу поиска не является очевидным. Напомним, что в алгоритме поиска Гровера идентифицируется целевой элемент i∗ в базе данных размера K путем итеративного применения предопределенного оракула Uy = I — 2 i у ii* и оператора диффузии
Umu= 21 ^М - I и И =^ L i l i)
к входному состоянию.
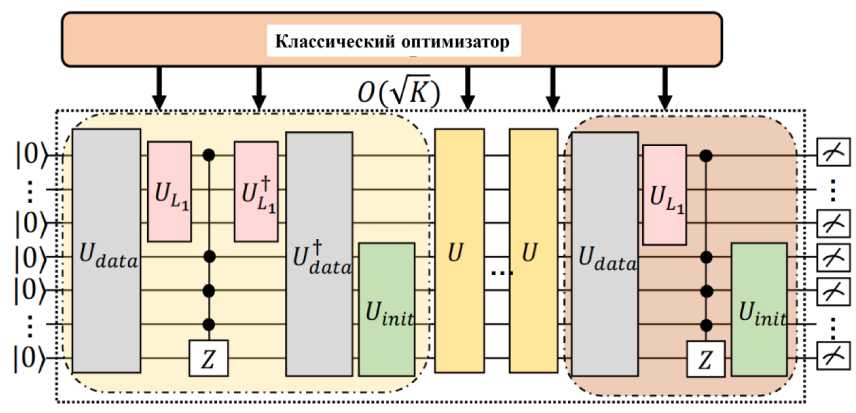
GBLS , как показано на рис. 21 а, использует заданную вариационную квантовую схему U и множество управляемых кубитов, расположенных вдоль оси Z ( MCZ ), для замены оракула U .
(а)
(б)
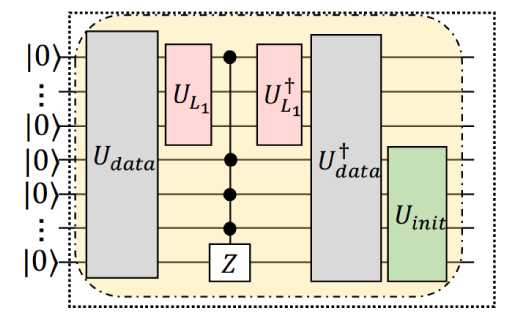
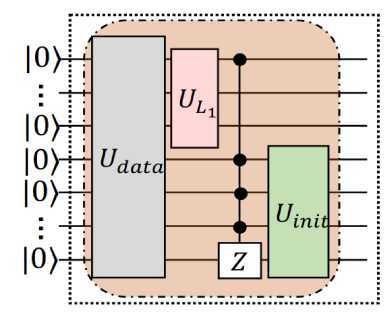
Рис. 21. Парадигма GBLS (а); Схемотехническая реализация оракула U (б); Схемотехническая реализация оракула UЕ (в)
(в)
В частности, вариационная квантовая схема условно переключает флаговый кубит (т.е. черную точку позади U , выделенную розовой областью) в зависимости от данных обучения. Обозначим все квантовые операции, относящиеся к одному циклу, как U, т.е., и := UntU,, (u, ® 1 )’= MCZ (U\ ® 1) Udta_
Оператор U , определенный в уравнении состоит из унитарных операторов (т.е. U data , UL , MCZ и U init ), выделенных затененной желтой областью (рис. 21 (б)). В последнем цикле используется единая операция U E , выделенная коричневой областью. Кубиты, взаимодействующие с UL (или U init ), формируют регистр функций (или данных).
После переобозначения, определяем Uini у = IF ® (21 ^^ | — IF ) с помощью | фф = — ^ . | i^ .
GBLS повторно применяет U к исходному состоянию 0 , за исключением последнего цикла, в котором примененные унитарные операции заменяются на
U e : = U .^ MCZ ( {и,,® I )о U data
,
как показано коричневой тенью на рис. 21 (в).
Следуя традиционному методу поиска по методу Гровера, GBLS запрашивает U и U E в общей сложности O ( у/K ) раз, прежде чем выполнять квантовые измерения. На этом завершается квантовая часть GBLS .
Вариационные квантовые схемы и метод оптимизации рассмотрим на примере вариационных квантовые схем U^ ( в ) , используемые в GBLS . Метод оптимизации, т.е. правило сдвига параметров, которое используется для обучения U рассмотрим ниже.
Вариационные квантовые схемы, как отмечалось ранее, также называются параметризованными квантовыми схемами и состоят из обучаемых одиночных кубитных элементов и двух кубитных элементов (например, CNOT или CZ ). В качестве схемы для устройств NISQ вариационные квантовые схемы были широко исследованы для решения задач генерации и распознавания образов с помощью вариационных гибридных квантово-классических алгоритмов. Одна из типичных вариационных квантовых схем называется многослойными параметризованными квантовыми схемами ( MPQC ), где расположение квантовых элементов в каждом слое идентично. Обозначим операцию, формируемую l -м слоем, как U ( в1 ) . Сгенерированное квантовое состояние из MPQC в виде
L
I ^ = П и в )| 0)® "
l =1
,
где L - общее количество слоев. GBLS использует MPQC для построения U , т.е.,
L и,, ( в ) = п и в ) l =1
.
Схема расположения l -го слоя U ( в1 ) показана на рис. 22.
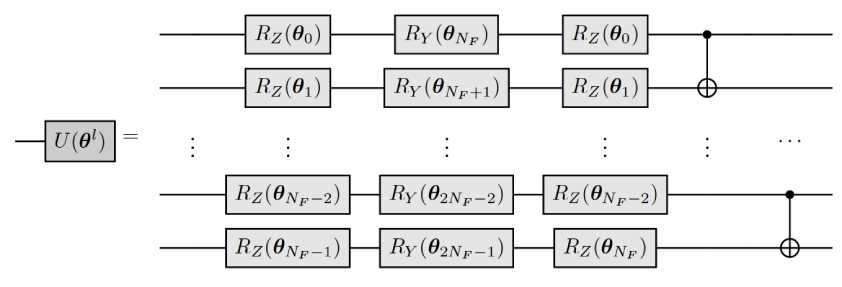
Рис. 22. Реализация l-го слоя U ( в1 )
Предположим, что l -й слой
-
U ( в1 ) взаимодействует с N F кубитами. Сначала к каждому кубиту
применяются три обучаемых параметризованных элемента, R , R и R , за которыми следуют N F – 1 CNOT -гейт.
Правило обновления на k -й итерации выполняется следующим образом t х dL ( 0(к ) , D, )
0( к + ! ) = 0 к ) — п
д0
,
где п _ скорость обучения, а D^ - k -й пример обучения.
Расширим явную форму функции потерь L ( 0 к ) , D^ ) Основываясь на механизме алгоритма поиска по Гроверу, функция потерь в задаче классификации для GBLS может быть записана в следующем виде: min L ( 0 ) : = sign I - — yk j Tr ( П р ( 0 ) ) , П = (| 1(1 |) O I o (| i 1 ( i *| ) относится к
оператору измерения, р(0) = UeU(0)O(^) 10)(0|(ueU(0)O(^K))
–
сгенерированное квантовое
состояние, а U ( 0 ) определена ранее (для ясности используем явную форму U ( 0 ) вместо U) .
Интуитивно понятно, что минимизированное значение L (0) соответствует тому факту, что в задаче классификации при yk = 1 (yk = 0) вероятность успешного выполнения выборки i*, а также получения первого функционального кубита, равного "1" ("0"), максимизируется (минимизируется). Для оптимизации GBLS использует метод, основанный на градиенте, т.е. правило сдвига параметров. Градиенты L (0^к), D^ ) можно переписать в виде dL (0(к 1, Dк) Г 1 'I01'1'
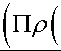
--------- = sign — у, --- d 0 I 2 к J д0
, где yk относится к метке последней записи в D; , sign( ) - обозначение знака функции, П - оператор измерения и р0к)) = UeU0к))
10><0| ( UeU (0к)) O(’]
. В результате, GBLS
dTr использует правило сдвига параметров для достижения градиента
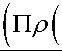
д0
.
Тогда правило обновления GBLS на t-й итерации для j-й записи таково дъ(в(к ),D.) Tr 0(к= 0(к)—п (j ) = 0Л)—п -j j d0 j
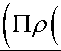
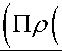
• Г 1
sign I 2
—
Ук I.
Учитывая обучающий пример x =(^(i),^(i))e0 2 для всех i e[N — 1], функция встраивания g(^fi),^(i)) :D2 ^D 4, которая используется для кодирования x. в квантовые состояния, формулируется как g(^i), с^i)) = (RY (g(суi), ayi)
, ^ 2
0 2 , где ф (г у 1 ) , ^ 2i ) )
-
указанная функция отображения.
Приведенная выше формулировка подразумевает, что g ( x i ) может быть преобразована в последовательность квантовых операций, где ее реализация проиллюстрирована на верхней левой панели Рис. 23. Чтобы одновременно закодировать несколько обучающих примеров в квантовые состояния, необходимо реализовать g ( x i ) в качестве контролируемой версии, где реализация показана на верхней правой панели рис. 23.
Верхняя левая панель иллюстрирует схемную реализацию кодирования унитарных данных Udata, соответствующая отображение характеристик объектов g(xi). Нижняя панель демонстрирует реализацию GBLS с учетом входных данных Dk =(xi, Xj, xk, xl), где реализация квантовой операции «controlled - g(xi)» показана на верхней правой панели.
Синтетический набор данных и производительность различных квантовых классификаторов в идеальных условиях представлены на рис. 24. На левой панели показан синтетический набор данных, используемый в численном моделировании. Условные обозначения "положительный" (или "отрицательный") означают, что метка данных равна 1 (или 0). Правая панель демонстрирует точность обучения и тестирования различных квантовых классификаторов.
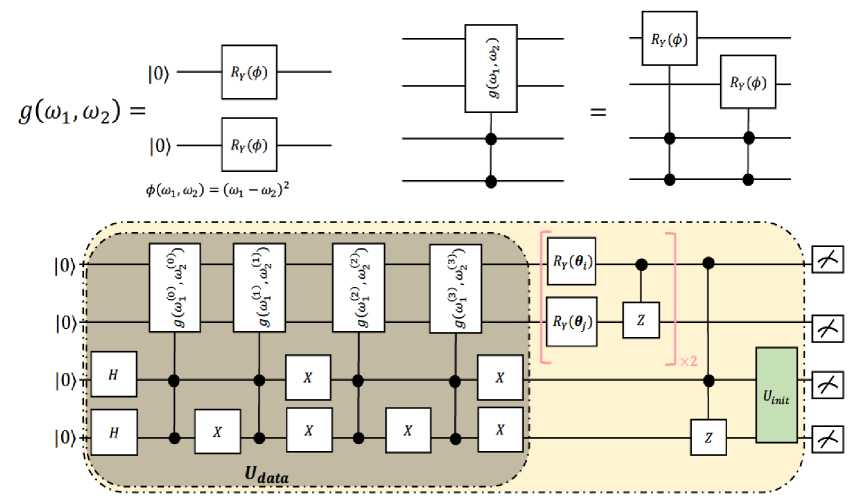
Рис. 23. Реализация GBLS, используемая при численном моделировании
Обозначения ‘ GBLS ’, " BCE", " MSE’ относятся к предлагаемому GBLS , классификатору квантового ядра с потерей двоичной перекрестной энтропии, и классификатору квантового ядра с потерей среднеквадратичной ошибки, соответственно. Вертикальные столбики отражают разницу в точности теста на каждой итерации.
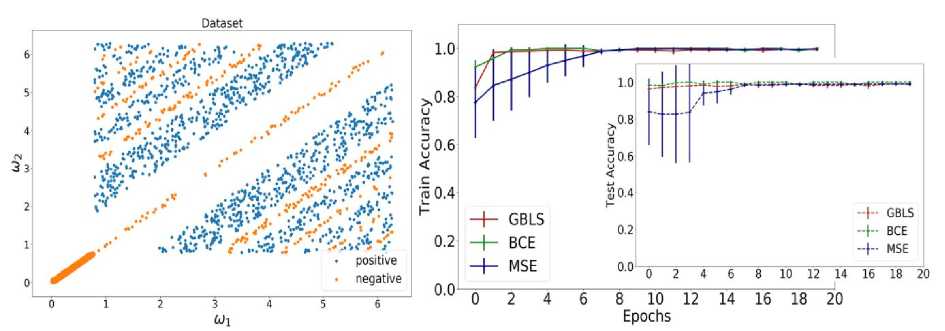
Рис. 24. Синтетический набор данных и производительность различных квантовых классификаторов в идеальных условиях
Выбор классификаторов квантового ядра в качестве эталонного основан на том факте, что этот метод обеспечивает современную производительность для классификации нелинейных данных.
Рассмотрим в качестве примера случай идеальной настройки. Оценим производительность различных квантовых классификаторов в идеальных условиях, когда квантовая система бесшумна, а количество измерений бесконечно. Правая панель на рис. 25 иллюстрирует усредненную точность обучения и тестирования в зависимости от количества периодов.
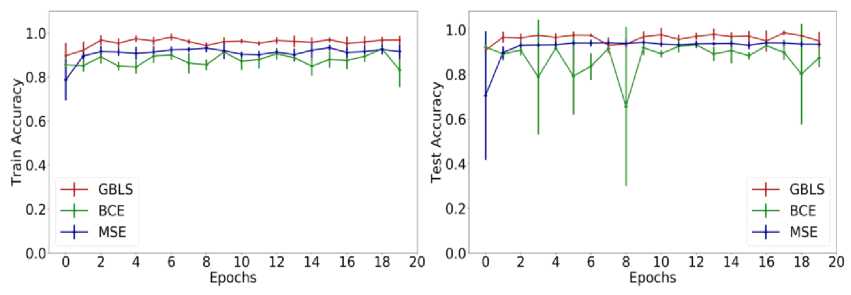
Рис. 25. Результаты моделирования различных квантовых классификаторов в режиме реалистичного шума
В частности, введенное предложение обеспечивает производительность, сравнимую с классификатором на квантовом ядре с потерей BCE , где точность обучения и тестирования достигает 99% в течение 2 эпох. Более того, эти два метода превосходят классификатор квантового ядра с потерей MSE , точность тестирования которого может достигать 95% только через 10 эпох. Разница в этих трех квантовых классификаторах после10 эпох становятся малой величиной, что означает, что все они сохраняют стабильную производительность при идеальных настройках. Между тем, шум измерения был применен ко всем квантовым классификаторам. Из-за относительно низкой производительности классификатора квантового ядра с потерей MSE , здесь сосредоточимся только на сравнении классификаторов GBLS и квантового ядра с потерей BCE и потерей MSE . Все настройки гипер-параметров идентичны тем, которые использовались в приведенных выше численных расчетах. Результаты моделирования представлены на рис. 25.
Обозначения " GBLS ", " BCE " и " MSE " имеют то же значение, что и на рис. 24. Модель шума, которая извлекается из реального квантового оборудования, применяется к обучаемому унитарному UL ( 0 ) из этих трех классификаторов. В частности, три классификатора обеспечивают сопоставимую производительность. Такие результаты свидетельствуют об эффективности GBLS , поскольку требуемое количество измерений для GBLS сокращено в четыре раза по сравнению с двумя другими квантовыми классификаторами. Численные эксперименты показали, что GBLS может достичь производительности, сравнимой с другими передовыми квантовыми классификаторами, за счет использования меньшего количества измерений и может найти применение в квантовых устройствах.
Существует два основных направления применения QNN . Первый использует QNN для генерации квантовых состояний, которые минимизируют ожидаемое значение данного гамильтониана, например, в вариационных квантовых решателях собственных значений ( VQE ) для задач квантовой химии или в алгоритмах квантовой приближенной оптимизации ( QAOA ) для комбинаторных задач. задачи оптимизации. Второй путь использует QNN в качестве моделей машинного обучения, основанных на данных, для формирования дискриминативных и генеративных задачи, для решения которых QNN могли бы обладать большей выразительностью, чем их классические аналоги. Несмотря на то, что в исследования QNN вкладывается все больше усилий, есть свидетельства того, что их будет трудно обучать из-за плоских ландшафтов оптимизации, называемых бесплодными плато. Альтернативная схема обучения QNN с помощью максимально когерентного (т.е. квантового) протокола представлена на рис. 26.
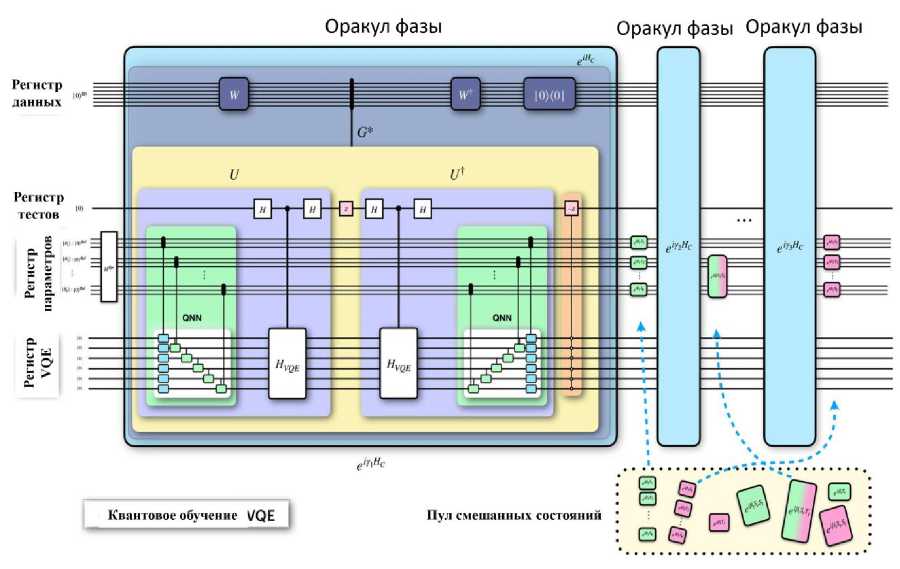
Рис. 26. Схема алгоритма квантового обучения для VQE
Здесь используется обучение VQE в качестве примера, чтобы представить принципиальную схему алгоритма квантового обучения для QNN .
Процесс квантового обучения может быть описан как эволюция состояния в совместном гильбертовом пространстве регистра параметров и регистра QNN . Их протокол квантового обучения состоит из двух чередующихся операций в режиме QAOA - первая операция воздействует как на регистр параметров, так и на регистр QNN , чтобы закодировать функцию стоимости QNN в относительную фазу состояния параметра. Вторая операция воздействует только на регистр параметров и представляет собой вариант оригинальных смесителей QAOA , адаптированный для случая, когда параметры в QNN являются непрерывными переменными. Эти две операции могут быть математически выражены как e YC(в ) и e 1вНм , где 0 - параметры QNN , C ( 0 ) - функция стоимости QNN , Y и в - настраиваемые гипер-параметры, H M - гамильтониан смешанных состояний. Ожидается, что благодаря эвристической настройке гипер-параметров квантовое обучение приведет к достижению оптимальных параметров QNN после нескольких итераций чередующихся операций QAOA .
Данный процесс проиллюстрирован чередующиеся операции их квантового обучения на рис. 27. Протокол квантового обучения состоит из двух чередующихся операций в режиме оптимизации алгоритма QAOA — первая операция воздействует как на регистр параметров, так и на регистр QNN , чтобы закодировать функцию стоимости QNN в относительную фазу состояния параметра. Эта операция представлена синими блоками на рисунке. Вторая операция воздействует только на регистр параметров и представляет собой вариант оригинальных смесителей QAOA , адаптированный для случая, когда параметры в QNN являются непрерывными переменными.
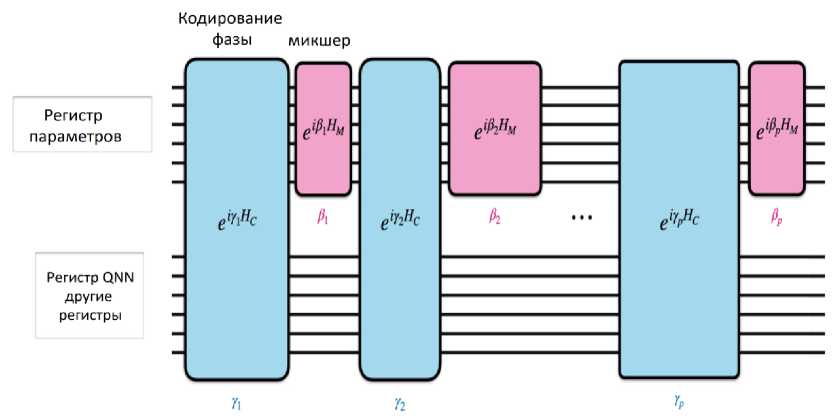
Рис. 27. Протокол обучения, аналогичный QAOA для QNN
Эта операция представлена розовыми блоками на рис. 27. Квантовое обучение может быть описано с помощью адаптивного алгоритма Гровера в качестве базовой линии перед внедрением системы квантового обучения с использованием QAOA .
Схема фреймворка для квантового обучения QNN представлена на рис. 28.
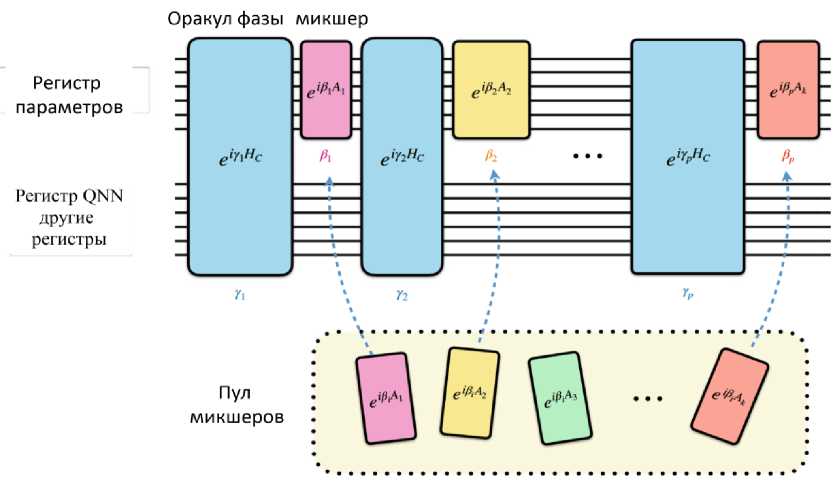
Рис. 28. Схема фреймворка для квантового обучения QNN
Примечание . Отметим некоторые фундаментальные различия адиабатического протокола и протокола QAOA . QAOA можно рассматривать как “упрощенную” версию адиабатической эволюции: гамильтонианы эволюции смешанных состояний являются начальным гамильтонианом в аналогичном адиабатическом алгоритме, а гамильтонианы затрат - конечным гамильтонианом. Однако QAOA с малой глубиной - на самом деле не оцифрованная версия адиабатической задачи, а скорее специальный отклик. QAOA способен детерминировано находить решение специально построенных задач оптимизации в случаях, когда квантовый отжиг не применим. В результате QAOA - алгоритм, основанный на учете помех, так что нецелевые состояния создают деструктивные помехи, в то время как целевые состояния создают конструктивные помехи.
На рис. 29 изображен этот процесс в виде интерференции QAOA . QAOA - алгоритм, основанный на учете помех, при котором нецелевые состояния создают деструктивные помехи, в то время как целевые состояния создают конструктивные помехи.
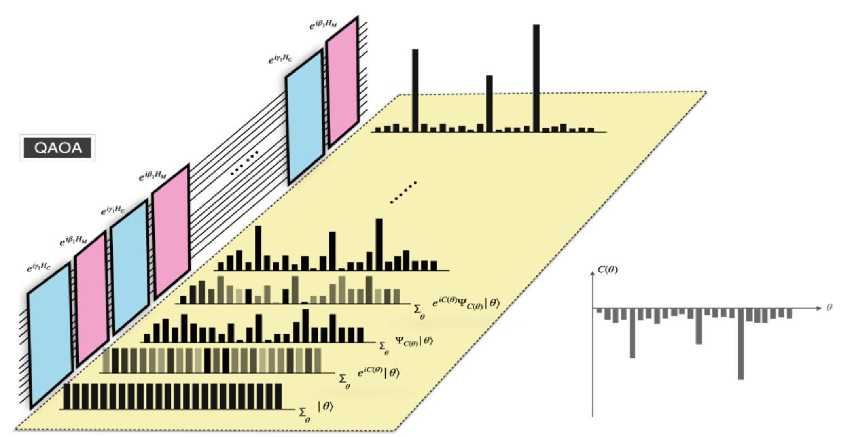
Рис. 29. Процесс интерференции QAOA
На рис. 29 иллюстрируется процесс взаимодействия, представляя эволюцию квантового состояния параметров (черные гистограммы на желтой плоскости) наряду с операциями QAOA (синие и розовые прямоугольники на линиях схемы, представляющие фазовое кодирование и смешанные состояния, соответственно). Начальное состояние ∑ θ } (без учета коэффициента нормализации) является состоянием суперпозиции наложения всех возможных конфигураций параметров.
После первой операции кодирования фазы состояние становится ∑ e-iC(θ) θ} , для чего используется непрозрачность столбцов, чтобы указать значение фазы; значения амплитуд в состоянии остаются неизменными. После первого смешивания состояние становится
∑ θ ψC ( θ ) θ>
в
котором значения амплитуд в состоянии изменились.
Аналогичный процесс происходит со следующими операциями до тех пор, пока амплитуды оптимальных конфигураций параметров значительно не увеличатся (самая дальняя гистограмма). Серая гистограмма в правом углу - функция затрат, оптимизируемая QAOA .
Квантовая схема операций в исходном QAOA представлена на рис. 30.
Состояние инициализируется применением вентилей Адамара к каждому кубиту, представленных в виде H ⊗ n . Это приводит к состоянию равномерной суперпозиции всех возможных решений. QAOA состоит из чередующейся временной эволюции по двум гамильтонианам HC и HM для p раундов, где продолжительность в раунде j определяется параметрами γ и β соответственно.
В исходном QAOA гамильтониан смешанных состояний HM выбран равным H= ∑n X
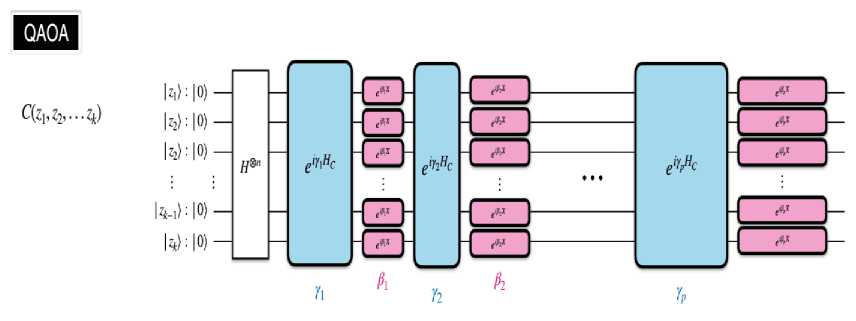
Рис. 30. Квантовая схема операций в QAOA
После всех p раундов состояние становится
\ R — - - i e P H M -~ i Y P H C -в H M ^- i 7 2 H C &~ в H M -~ i 7 1 H C I
I в , Y i — e e •••e e e e s /
Алгоритм Гровера обычно используется в качестве метода поиска для нахождения набора желаемых решений из набора возможных решений. На практике применяют алгоритм Гровера для глобальной оптимизации, который называется адаптивный поиск Гровера - Grover Adaptive Search ( GAS ).
GAS был применен для обучения классических нейронных сетей и полиномиальной бинарной оптимизации. Отметим особенности GAS .
Рассмотрим функцию f : X ^ , где для простоты представления предположим, что
X — { 0,1 } }
Нас интересует решение
min
Х Е X
f ( x ) . Основная идея GAS заключается в построении
“адаптивного” оракула для заданного порогового значения y таким образом, чтобы он отмечал все состояния x ∈ X, удовлетворяющие f (x) < y, а именно оракул отмечает решение x тогда и только тогда, когда другая логическая функция gy удовлетворяет gy (x) — 1, где gy (Х) —'
1 если f ( x ) < y 0 в другом случае
. Затем оракул OГровер
действует как 0 Гровер | x ) — ( - 1 ) g y ( x ) | x)
Алгоритм Гровера выполняет поиск, чтобы найти решение x со значением функции, лучшим, чем у . Затем устанавливает y — f ( Х ) и повторяет до тех пор, пока не будут выполнены некоторые формальные критерии завершения - например, на основе количества итераций, времени или прогресса в y .
Обсудим использование адаптивного поиска GAS для выполнения глобальной оптимизации структуры QNN . Как представлено ранее, ядром адаптивного поиска GAS является адаптивный оракул, определенный как O . Рассмотрим кратко, как создать такой оракул для обучения QNN .
Адаптивный O оракул Гровера в контексте обучения QNN выступает в следующем виде:
ОГровер | 0 ®| 0)QNN+a,cb —(- 1 ) g ( ' ' ^ ®| 0QNN+anaUaS , в котором C * - адаптивный порог для функции затрат, а функция g определяется как
g ( Х )— ^
1 x < 0
0 в других случаях
.
Когда ОГровер воздействует на состояние суперпозиции параметров У ^|0 , имеем
О Гровер Х^в) ®| OJ oNN+a.^ — У ( - 1 ) g ( C" C 'I «,,") ®1 0
О
QNN с оракулом OГровер может быть создана с помощью следующих шагов.
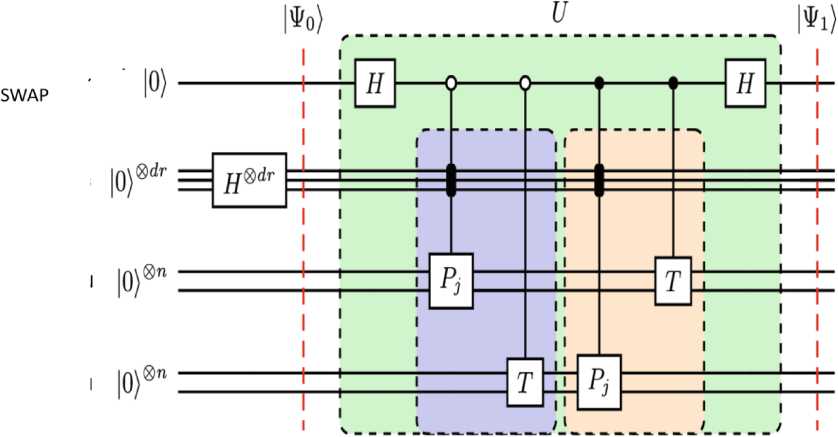
Амплитудное кодирование . Первым шагом является кодирование функции затрат QNN в амплитуду. В зависимости от формы функции затрат QNN амплитудное кодирование может быть достигнуто с помощью теста swap или теста Адамара. Рассмотрим амплитудное кодирование с помощью swap - теста. Для задачи обучения чистое состояние | ^ ) — T 10^ ( T - заданный унитарный оператор) функция стоимости представляет собой точность между сгенерированным состоянием из QNN и состоянием ^^ — T |0). В этом случае амплитудное кодирование может быть достигнуто с помощью теста, как показано в схеме на рис. 31.
Дополнительный кубит
Регистр QNN
Регистр QNN
Рис. 31. Амплитудное кодирование с помощью swap – теста
Регистр параметров
Обозначим унитарный оператор для схемы swap – теста (выделенной зеленым прямоугольником) как U , а входное и выходное состояния U как | ^ ^и | ^ ) соответственно. Входные данные для U ,
| ^ ) , могут быть описаны в виде:
। ^ о>=i о) ® si j ®i о) ;„ jo) Q ,» 2. V j J
Тогда оператор U может быть записан явно в виде
U :=[H®I®I®I]•
10)<0|® si j}^j I® P j ®T +1 OOI® XI jW 1® P j ® T
•[ H ® I ® I ® I ]
Таким образом, Pj представляет QNN со специфической конфигурацией параметра, определяемой его управляющей битовой строкой j. Это представление применимо не только к одному гейту вращения, но и к случаю, когда имеется несколько параметризованных гейтов вращения. Можно доказать, что U можно переписать как U = XI j{j|®U, где U - единичное j значение индивидуального swap – теста для унитарного Pj и целевого унитарного T, определяемое как Uj := [H®I®Iр||0^01®P ®T +11)(1|®T®P]•[H®I®I]. Результирующее состояние U}., действующего на ^о) , равно | J = Uj |0®|0Qnn 110)Qnn2
и имеет следующий вид: ф^ = sin0 u} у|0) + cos000 |1) . Следовательно, конечное выходное состояние из U, 0J = U |^0^, равно
I ^ i)= XI Л ( sin 0 U0)+ cos 0 |j 11 ) = XI j I0) jj
Таким образом, функция стоимости
(точность pt ) для различных параметров была закодирована в амплитуды состояния 11^1 ^ .Поскольку анализ для случая теста Адамара очень похож на анализ для теста swap, опускаем здесь подробности.
-
2 . Оценка амплитуды . Вторым шагом, следующим за амплитудным кодированием, является использование оценки амплитуды для извлечения и сохранения функции стоимости в дополнительном регистре, который называется “регистром амплитуды”. Далее подробно рассмотрим оценку амплитуды. После амплитудного кодирования с помощью теста swap вводим дополнительный регистр |0^ампли^а, и выходное состояние | ' ^ (используя ту же запись) становится
I ^=ZI J | j |o)
t
амплитуда
где
может быть
разложено
в виде
ф\ = ~1= [е‘в' юф — e( j ^ } |. Следовательно, имеем
J/ 22 +,J 1 j/j
। 'J (e”j
— e i (— j
t амплитуда
Общий Гровер - оператор G определяется как G := UC2U 1Cl, где C 1 - вентиль Z на вспомогательном кубите swap, а C2 - унитарное «инверсное нулевое состояние». Можно показать, что оператор G может быть выражено как G = У| J^j |® Gj, где Gj - индивидуальный Гровер - оператор, как определено в: Gj = UCU' (Z 0 102n), где Z = |0^0| —11^1| - оператор Паули-Z;
C = I 0 ( 2 n + 1 ) — 2|oy
0 ( 2 n +1 )
I 0 ( 2 n +1 )
.
Описанную процедуру и далее алгебраические процедуры вычисления ' 2),| ' ),| '^ можно проиллюстрировать схемой [35-38], показанной на рис. 32.
Регистр параметров
Кубит амплитуды
Дополнительный кубит SWAP
Дополнительный кубит фазы
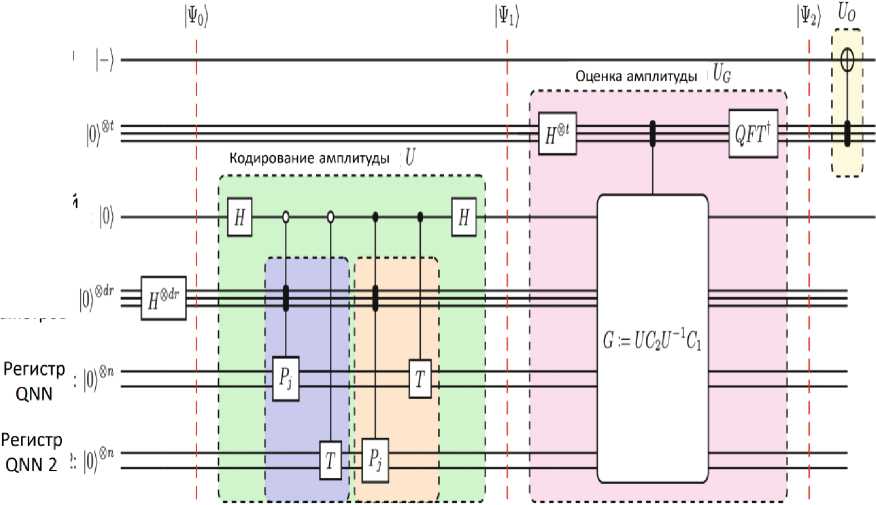
Рис. 32. Основные этапы создания оракула Гровера
Шаг 0: инициализируем систему, применяя гейты Адамара к регистру параметров, что приводит к состоянию
I ' о) = 10) s ®(Z j| j »®l 0) QnJO) \
Шаг 1 (зеленый прямоугольник с пунктиром): амплитудное кодирование функции затрат, как показано на рис. 32; в результате чего получается состояние
I ^1)=E jlj (sinjjl0)+cosVj |j|i>) , в котором Qi содержит функцию стоимости;
Шаг 2 (розовая рамка с пунктиром): оценка амплитуды для извлечения и сохранения функции стоимости в дополнительном регистре, который называется “регистром амплитуды”, в результате чего получаем состояние
I ^)=^j— (e wij ы j I2j-eij j} h-bhj
;
Шаг 3 (желтая рамка с пунктиром): пороговый оракул кодирует функцию затрат в относительную фазу с помощью вспомогательного кубита фазы, что приводит к состоянию
I^3>=jН)*-^ewlJЫ»-ei-,JljЫj -2j)
Опуская вычисление | ^ 4 ) , выполняем вычисление swap теста, в результате получаем следующее состояние
। ^=хн> g (?^"'\ j 1°> Qnn iio> ;„ 2 ни а...........
j
Как видно из данного уравнений, на вышеуказанных этапах был реализован оракул Гровера O . После описанной выше процедуры к состоянию параметра была последовательно добавлена относительная фаза, которая зависит от функции стоимости QNN pPj\^\ и порогового значения. Важно отметить, что вычисление позволяет отделить регистр параметров от QNN и других регистров.
-
3 . Обучение QNN с помощью адаптивного QAOA . Как показано на рис. 28, система квантового обучения QNN состоит из двух основных компонентов:
-
- Фазовый оракул . При этом функция стоимости QNNs последовательно кодируется в относительную фазу состояния суперпозиции в гильбертовом пространстве параметров;
-
- Адаптивные микшеры . Они используют скрытую структуру в задачах оптимизации QNN и, следовательно, могут обеспечить реализацию схем малой глубины.
Взаимодействия фазового оракула и адаптивных микшеров образуют процедуру QAOA , которая количественно определяет оптимальные параметры сети QNN .
Из-за характера алгоритма Гровера, основанного на глобальном поиске, квантовое обучение с использованием адаптивного поиска Гровера может обойти помехоустойчивое бесплодное плато; однако оно имеет определенные ограничения и недостатки, такие как: (1) не может справиться с вызванным шумом бесплодным плато; (2) требует экспоненциального числа вызовов к «контролируемому QNN » с чрезмерной длиной цепи и временем работы. Напротив, описанное квантовое обучение с совместным использованием адаптивного непрерывного QAOA может устранить ограничения, связанные с использованием адаптивного поиска Гровера.
Обсудим применение QNN в качестве квантового классификатора, который выполняет контролируемое обучение, что является стандартной задачей в машинном обучении.
Пример: Обучение квантового классификатора. Модель обучения, как и ранее, имеет следующий вид. Предположим, что X - набор входных данных, а Y - набор выходных данных. Задан набор данных D = {(xx, ух),..., (xM, ум )} из пар так называемых обучающих входных данных xm Е Xy и выходных данных цели обучения yw Е Y для m = 1, ..., M, задача модели обучения состоит в том, чтобы предсказать выходные данные yw е Y для нового входного сигнала хт Е Xy. Для простоты в дальнейшем будем предполагать, что X = □ N и Y=м. что является задачей бинарной классификации в N-мерном реальном входном пространстве. Таким образом, квантовый классификатор нацелен на изучение эффективной функции маркировки Хх X ^ Y .
Учитывая входные данные xt и набор параметров в , квантовый классификатор сначала вводит xt в состояние квантовой системы с n -кубитами через схему подготовки состояния Sx таким образом, что Sx 1 0^ = | ^ ( x )^, а затем использует обучаемую квантовую схему U ( в ) ( QNN) в качестве модели прогноза для принятия решений. Предсказанная метка класса y ( i ) = f ( x ,0^ извлекается путем измерения указанного кубита в состоянии U ( 0^ (р ( x )^. Схема квантового классификатора представлена на рис. 33.
Таким образом, согласно рис. 33, и как предварительно отмечено выше, для точки обучающих данных ( x , у. ) (слой ( x , у .) , см., рис. 33) квантовый классификатор сначала вводит xt в состояние квантовой системы с n -кубитами через схему внедрения данных Sx (фиолетовая рамка) таким образом, что Sx |0^ = | ^ ( х )^ и впоследствии использует обучаемую квантовую схему U ( в ) ( QNN) в качестве модели логического вывода (здесь, для простоты, используем один и тот же символ в для всех углов различных гейтов вращения R ( 0 ) в слое QNN) . Предсказанная метка класса У ( i ) = f ( x , 0 ) извлекается путем измерения указанного кубита в состоянии U ( 0 )| ф ( х )^ .
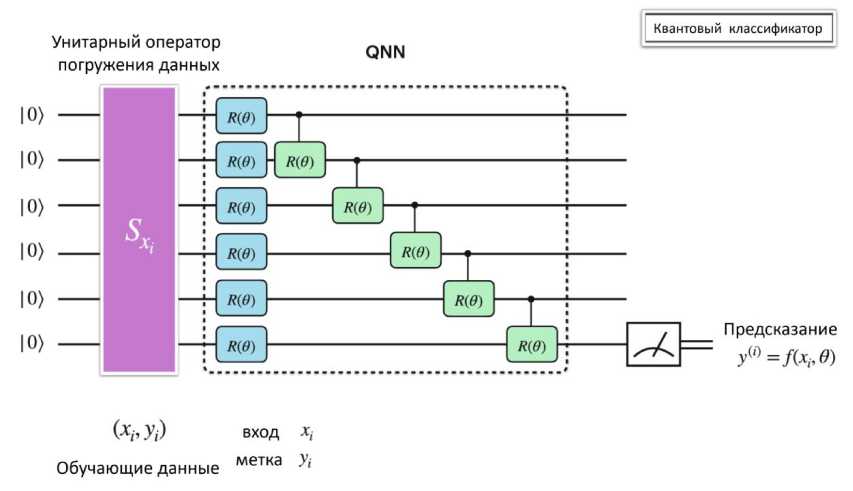
Рис. 33. Схема квантового классификатора
Примечание . Вариационный квантовый классификатор может работать как много классовый классификатор, здесь ограничиваемся случаем бинарной классификации, рассмотренным выше, и рассматриваем задачи с несколькими метками как набор подзадач бинарного распознавания.
Обозначим p ( Л ) как вероятность того, что результат измерения на указанном кубите будет равен Л ( Л е { 0,1 } ) . Функция стоимости каждой точки обучающих данных L ( 0 ) , как функция уг и у ( i ) , и, следовательно, функция y z, х. , в , которую обозначаем как L ( xt , y z, в ), выбирается как вероятность получения результата измерения на проектируемый кубит, идентичный заданной метке, а именно L i ( в ) = L ( xt , у. , в ) := p ( y i ). Тогда стоимость каждой выборки данных естественным образом закодирована в амплитуде выходного состояния QNN .
Здесь следует отметить, что чем больше вероятность, тем точнее прогноз, поэтому следует максимизировать затраты (чтобы соответствовать предыдущему описанию, используем “затраты” вместо обычно используемого “вероятности” для определения правильной метки для данных образец.)
С другой стороны, квантовое состояние системы (после подготовки состояния и вывода QNN ) можно записать в вид е
I к(0 )) = U ( ° )| ^ ( x , )) = p j 0o) 10 W + 71 - 7 (0) 11 Ы
_ 7 p ( y ) |°)ю+71 - p ( y , ) 11 Ю , y =0
. 7 p (y) 10 ю+J-ppM 11 ы, y,-=1
в котором 1^), | и ) - некоторое нормализованное состояние, зависящее от 0 .
Таким образом, стоимость каждой выборки данных L ( x , y , θ ) естественным образом кодируется в амплитуде выходного состояния | ^ ( О )) QNN . Амплитудное кодирование функции затрат для квантового классификатора показано на рис. 34.
Кодирование амплитуды функции стоимости
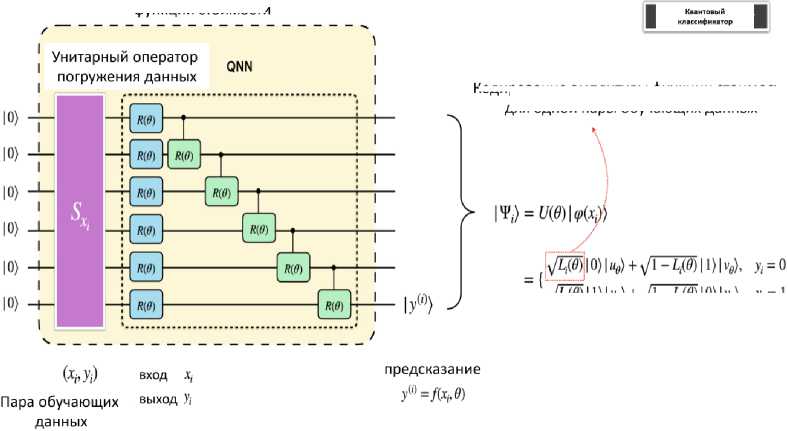
^ я = для L,{e):=L(xi,yi,O)=p(yi)
функция стоимости определяется для одной пары обучающих данных
Рис. 34. Амплитудное кодирование функции стоимости для квантового классификатора
Кодирование амплитуды функции стоимости для одной пары обучающих данных
Построение “управляемой QNN ” позволит параллельно кодировать амплитуду для всех конфигураций параметров.
Фазовое кодирование функции общей стоимости может быть реализовано путем накопления индивидуального фазового кодирования для каждой обучающей выборки; этот процесс можно проиллюстрировать на рис .35.
Оракул фазы
Регистр параметров
Регистр QNN другие регистры
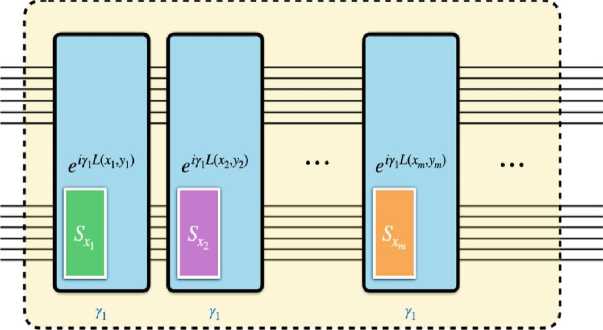
gt^ao} _ gt^^^Wm)
Рис. 35. Фазовое кодирование функции общей стоимости квантового классификатора
Функция общей стоимости всего обучающего набора может быть определена как C 0 ) = У L ( Xi ’ y 0 ) . Следовательно, фазовое кодирование функции общих затрат (общий желтый прямоугольник) может быть реализовано путем накопления индивидуального фазового кодирования для каждой обучающей выборки (синие прямоугольники). Внутренние ячейки в синих полях представляют различные варианты встраивания данных для точек обучающих данных
На основе фазового кодирования функции общей стоимости, можем построить полный протокол квантового обучения, как показано на рис. 36.
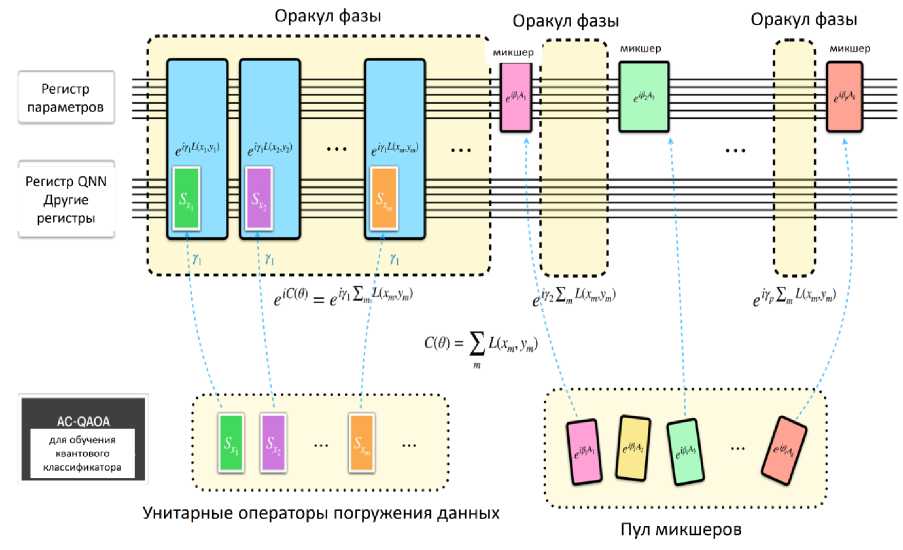
Рис. 36. Схема протокола квантового обучения для квантового классификатора
Полный протокол квантового обучения состоит из чередования фазового оракула, который обеспечивает согласованное фазовое кодирование функции затрат, и адаптивных микшеров, выбранных из пула микшеров. Фазовое кодирование функции общей стоимости для квантового классификатора подробно показано на рис. 35. Функция общей стоимости всего обучающего набора может быть определена как C(0) = У L(xi,yi,0). Отсюда следует, что e-‘C(0^П,е-"L(x yi'в) • Следовательно, фазовый оракул для функции общей стоимости (желтые прямоугольники в верхней части этого рисунка) может быть реализован путем накопления индивидуального фазового кодирования для каждой обучающей выборки (синие прямоугольники). Цветные прямоугольники с белой каймой представляют различные варианты встраивания данных для точек обучающих данных. Цветные прямоугольники с черной каймой (за исключением синих для фазового кодирования) представляют различные выбранные микшеры.
После каждого измерения в регистре параметров получаем конкретную конфигурацию параметров QNN . Затем необходимо оценить функцию затрат для этой конкретной конфигурации параметров. Количество запусков QNN после каждой шкалы измерений равно O ( 1/ ^ ) , а общее количество QNN запусков всех измерений во время квантовой шкалы обучения равно ( 1
^ QNN О O — J N H3Mepений . Для небольшого примера с 5-ю кубитами и 10 вентилями вращения в QNN для реализации протокола требуется примерно 60 кубитов. Таким образом, протокол реализуем на малых квантовых компьютерах.
Заключение
Рассмотрены цели и методы квантового машинного обучения как программно-алгоритмической платформы квантового «сильного» вычислительного ИИ. Приведено описание архитектуры и принципов работы трех наиболее применимых в квантовой инженерии методов квантового машинного обучения и области применения рассмотренных методов. Применение QNN рассмотрено в качестве квантового классификатора, который выполняет контролируемое обучение, что является стандартной задачей в машинном обучении.


