Модели молекулярной динамики: обзор EAM-потенциалов. Часть 1: потенциалы для однокомпонентных систем

PNRPU MECHANICS BULLETIN

Физические механизмы пластической деформации проявляются в эффектах локализации пластического течения, имеющих многомасштабный характер. При этом пластическая деформация протекает коррелированно по всему объёму образца [1–3].

В работе [4] выделены стадии процесса деформации при сопоставлении последних с данными о распределении зон локализации пластического течения, что позволило установить универсальный сценарий коррелированного поведения многомасштабных зон локализации пластической деформации, практически не зависящий от конкретных деталей механизма деформации и структуры деформируемого материала.

К основным закономерностям могут быть отнесены следующие [4]:

• –    локализация возникает самопроизвольно при постоянной скорости растяжения образцов и не требует для своего появления специального воздействия;

• –    картины локализации последовательно меняются по мере развития пластического течения закономерным образом, а их эволюция тесно связана со стадийностью течения;

• –    на некоторых стадиях картины локализации обладают отчётливо выраженной пространственной и временной периодичностью;

• –    каждая из картин локализации, как и явления на соответствующей стадии процесса течения, связаны с определённым микроскопическим механизмом деформационного упрочнения, действующим на этой стадии;

• –    дефектная структура материала и деформационное упрочнение необратимо изменяются при пластической деформации, инициируя нелинейный характер развития макроскопического пластического деформирования.

Закономерности явлений микролокализации пластического течения показывают, что картины локализации суть автоволновые процессы в активных средах. Отождествляя картины локализации пластического течения с соответствующими типами макроскопических автоволновых процессов, можно полагать, что

• –    на стадии площадки текучести реализуется автоволна переключения;

• –    на стадии линейного деформационного упрочнения возникает фазовая автоволна;

• –    на стадии упрочнения по Тейлору формируется стационарная диссипативная структура;

• –    на стадии предразрушения наблюдается коллапс автоволнового процесса.

Таким образом, в ходе пластической деформации материалов закономерным образом последовательно меняется тип генерируемых средой автоволновых процессов.

Проявлением локализации пластической деформации на стадии упрочнения материала является прерывистое деформирование (эффект Портевена-Ле Шателье), которое характерно для широкого класса пластичных материалов при определённых температурно-скоростных условиях деформирования и проявляется в виде образования многочисленных срывов нагрузки на диаграмме нагружениях [5–8].

Физическое происхождение эффекта Портевена-Ле Шателье – динамическое взаимодействие двух групп дефектов, а именно подвижных дислокаций и растворенных атомов. Мобильные дислокации, которые являются носителями скорости пластической деформации, движутся «рывками» между препятствиями, создаваемыми другими дислокациями. Растворенные атомы диффундируют в поле напряжений, создаваемом подвижными дислокациями, и дополнительно закрепляют их на препятствиях. Когда система находится в определённом диапазоне скоростей деформации и температур, время диффузии атомов растворенного вещества имеет порядок времени ожидания дислокаций на препятствиях, может иметь место отрицательная зависимость силы от скорости дислокаций, которая в масштабе образца преобразуется в отрицательную деформационную чувствительность напряжения. Как следствие классическая картина эффекта Портевена-Ле Шателье заключается в неустойчивости однородного состояния деформации, обусловленной аномальной отрицательной чувствительностью к скорости деформации. Неустойчивость проявляется в зарождении зон локализованной пластической деформации с типичной шириной 10–100 нм, каждая их которых связана с падением напряжения кривой зависимости напряжения от времени. В зависимости от температуры и скорости деформации эти полосы могут распространяться и не распространяться вдоль образца. Существуют также различные случаи пространственно-временной корреляции областей локализованной деформации, приводящих к различным сценариям деформационного поведения [9, 10].

В данной работе представлены результаты экспериментов по сжатию поликристалличе-ских образцов из сплава АМг6. В отличие от эксперимента на растяжение, сжатие позволяет получить большую деформацию (до 80 %) без разрушения образца. Далее результаты были интерпретированы с точки зрения физики неравновесных критических явлений [11, 12].

Работа содержит результаты исследований фундаментальных закономерностей развития пластичности, проявляющиеся наиболее ярко на сплавах Al-Mg, обнаруживающих множественные многомасштабные неустойчивости пластического течения, обусловленные коллективным поведением дефектов. В работе впервые показано, что развитие неустойчивостей связано с новым типом критических явлений в твердых телах с дефектами (структурно-скейлинговые переходы), определяющих локализацию пластического течения и переход к разрушению. В настоящей работе подтверждены сопоставлением результатов, полученных обработкой оригинальных данных о статистических распределениях временных интервалов флуктуаций напряжений пластического течения, и оригинальных данных профилометрии рельефа поверхности деформированных образцов признаки «критического» поведения материала при развитии пластического течения сплава. Важным результатом фундаментального характера является также сопоставление проявлений неустойчивости при развитии пластического течения данного сплава (негауссовый характер интервалов следования флуктуаций напряжений пластического течения) с установленными в [13–16] признаками коррелированности флуктуаций момента при развитом турбулентном течении жидкостей (течение Кармана). Представленные в статье результаты имеют фундаментальное значение и подтверждают впервые высказанное в работе автора [17] предположение о возможности квазипластического механизма переноса импульса при развитом турбулентном течении при больших числах Рейнольдса.

Экспериментальная часть

Эксперименты проводились на цилиндрических образцах диаметром 15 мм, высотой 22,5 мм и наклоненных на 2° от вертикали (рис. 1). Данная форма образцов создаёт преимущественное направление образования деформационных полос скольжения, что позволяет достичь больших деформаций (до 80 %) без разрушения. Деформация определялись через изменение размеров образца в виде отношения разности исходной и текущей высоты образца на исходную высоту образца.

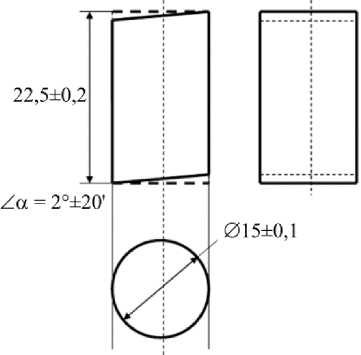
a

Рис. 1. Геометрия образца ( а ); образец в испытательной машине ( б )

Fig. 1. Sample geometry ( a ); sample in the test installation ( b )

б

Образцы были выполнены из сплава АМг6 (состав представлен в таблице) и предварительно отожжены при температуре 450 оС в течение 3 часов с последующим остыванием в печи.

Химический состав исследуемого сплава (в процентном содержании) Chemical composition of the studied Al-Mg alloy (in weight %)

Al	Cu	Mg	Mn	Si	Fe	Zn	Be	Ti
91,1–93,68	0,10	5,8–6,8	0,5–0,8	0,4	0,4	0,20	0,0002–0,005	0,02–0,1

Сжатие производилось при комнатной температуре на испытательной электромеханической машине Shimadzu AG-300 со скоростью перемещения захвата 1–4 мкм/с.

Деформационная диаграмма алюминиевого сплава представлена на рис. 2 и демонстрирует множественные флуктуации напряжения течения, обнаруживающие различную динамику на разных участках деформационной кривой.

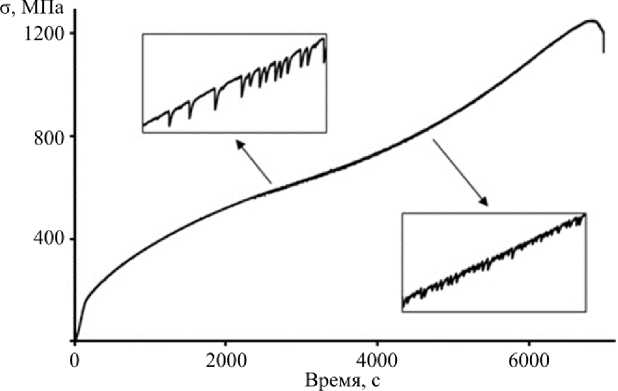
Рис. 2. Деформационная диаграмма алюминиевого сплава АМг6 при скорости перемещения захвата 2 мкм/с

Fig. 2. Deformation diagram of Al-Mg alloy at the velocity of the grip 2 μm/s

На основании [11] исследовалась временная последовательность флуктуаций «время ожидания» между событиями (рис. 3), которая демонстрирует степенные зависимости вида τ= A 1 ( ε-ε c 1 ) ^-β 1 и τ= A 2 ( ε c 2 -ε ) ^-β 2 в окрестности двух значений макроскопических деформаций ε c 1 и ε c 2 . Здесь A 1 , A 2 , β 1 , β 2 – некоторые эмпирические константы, зависящие от скорости деформации образцов. Данные значения соответствуют начальной стадии

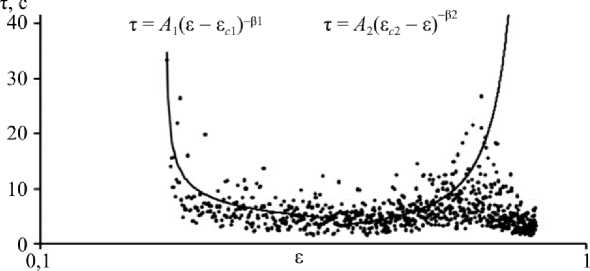
Рис. 3. Зависимость интервалов времени между конечно-амплитудными флуктуациями напряжения течения алюминиевого сплава АМг6 при скорости перемещения захвата 2 мкм/с

Fig. 3. The time dependence between finite amplitude fluctuations of the flow stress aluminum alloy АМg6 with the velocity of the grip 2 μm/s развития конечно-амплитудных флуктуаций в условиях локализации пластической деформации и стадии перехода к новому сценарию локализации деформации, предшествующей образованию очагов разрушения. По аналогии с теорией критических явлений значения 8c 1 и 8c2 могут рассматриваться как аналоги критических точек, в окрестности которых наблюдается резкое увеличение характерных времен «релаксации» [18].

Переход через вторую «критическую точку» 8 c2 , в отличие от результатов [11], не сопровождался разрушением образца, но обнаруживал развитие флуктуаций с качественно новой пространственно-временной динамикой, которая может быть ассоциирована с формированием областей локализации поврежденности, предшествующих зарождению макроскопических трещин [19].

Плотность функции распределения флуктуации интервалов времени между конечноамплитудными флуктуациями напряжения пластического течения σ в переменных ln P ~(ln t – t>)/Dt, вычисленная для среднего участка диаграммы интервалов времени с выраженной перемежаемостью флуктуаций напряжения пластического течения, представлена на рис. 4.

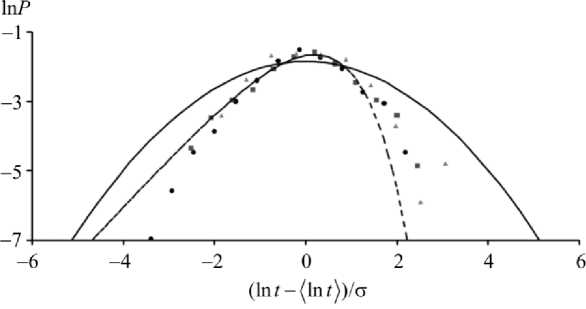
Рис. 4. Плотность распределения флуктуаций времени на стадии пластического течения для сплава Al-Mg. Экспериментальные данные показаны: • – для скорости деформации 1 мкм/с; ■ – для скорости деформации 2 мкм/с; ▲ – для скорости деформации 4 мкм/с; показан расчёт функции плотности вероятности для логнормального распределения: ▬ выполненный по формуле (1), ▬ ▬ выполненный по формуле (2)

Fig. 4. Density distribution of time fluctuations at the stage of plastic flow for the Al-Mg alloy. Experimental data are shown: • – for the imposed compression speed of 1 μm/s, ■ – for the imposed compression speed of 2 μm/s, ▲ – for the imposed compression speed of 4 μm/s; calculation of the probability density function for the lognormal distribution: ▬ is executed according to the equation (1), ▬ ▬ is executed according to the equation (2)

Функция стандартного логнормального распределения

P =--;= exp

D t V2n

( ln t - (in t )) 2

2 D_t²

нормированная на величину стандартного отклонения D t флуктуации интервалов времени между конечно-амплитудными флуктуациями напряжения течения, обнаружила негаус-совый характер.

В [13–16] экспериментальное исследование развитого стационарного турбулентного течения (схема Кармана – турбулентность в замкнутом объёме, инициированная вращающимися дисками) позволило установить, что функция плотности вероятности для конечно-амплитудных флуктуаций момента может быть представлена с высокой точностью в виде

P ( y ) = K exp ( x ( y ) - e x ⁽ y ) ) a . (2)

Здесь K, b, s - некоторые эмпирические константы; x = b ( y - s ) ; a = n /2; y = ( In t - (ln t ) / / D_t .

Анализ результатов также показал «подчинённость» статистики флуктуаций интервалов времени между конечно-амплитудными флуктуациями напряжения течения данному виду функции плотности распределения вероятности. Данное соответствие позволяет высказать предположение о «квазипластическом» механизме развития неустойчивостей, лежащих в основе закономерностей скейлинга при развитом турбулентном течении жидкостей при больших числах Рейнольдса [17, 20–23].

Развитие локализации пластического течения, обусловленного коллективным поведением ансамблей дефектов, исследовалось методами структурного анализа морфологии поверхностного рельефа с использованием оптического интерферометра-профилометра NewView-5010 для последующего вычисления масштабного инварианта (показателя Хёрста) и пространственного масштаба области, на которой наблюдается коррелированное поведение микросдвигов. Определение показателя Хёрста деформационных дефектных структур может дать физическое объяснение универсальности критических явлений применительно к сценариям пластической неустойчивости и перехода к разрушению для различных классов материалов и связи состояния структуры с «пороговыми» характеристиками перехода пластически деформированного материала к разрушению [24–29].

Поверхностный рельеф (рис. 5) вдоль (предварительно отполированной) боковой поверхности деформированных образцов регистрировался с помощью интерферометра-профилометра высокого разрешения New-View (при увеличении x500) и затем анализировался методами фрактального анализа для определения условий коррелированного поведения многомасштабных дефектных структур.

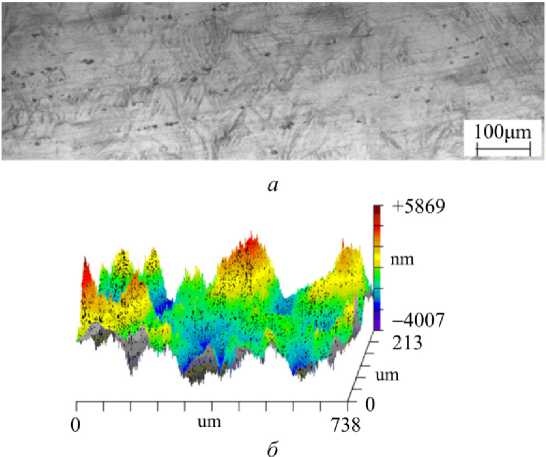
Рис. 5. Оптическое изображение ( а ) и 3D-образ поверхности после деформирования ( б ) (при деформации 15 %) Fig. 5. Optical image ( a ), 3D image of the surface after deformation ( b ) (deformation 15 %)

По одномерным профилям рельефа поверхности разрушения (рис. 6, а ) вычислялась функция K ( r ) по формуле

K ( r ) = {( z ( x + r )

z ( x )) ²

1/2

• да r , x

где K ( r ) – усредненная разность значений высот рельефа поверхности z ( x + r ) и z ( x ) на окне размером r ; H – показатель Хёрста.

Представление функции K ( r ) в логарифмических координатах (рис. 6, б ) позволяет провести оценку показателя структурного скейлинга H (показателя Хёрста) как пространственного инварианта, определяемого постоянством наклона зависимости log 2 K ( r ) от log 2 ( r ).

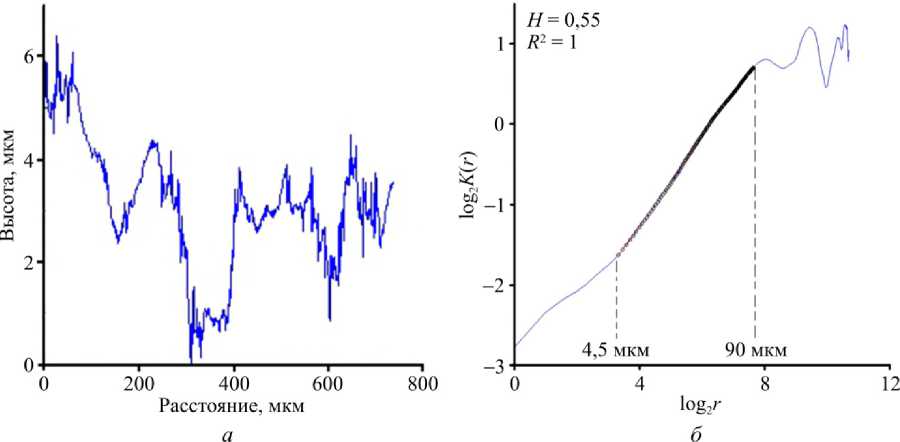
Рис. 6. Характерный одномерный профиль ( а ); вид зависимости log 2 K ( r ) от log 2 ( r ) для поверхности после деформирования (при деформации 15 %) ( б ) Fig. 6. Characteristic one-dimensional profile ( a ); form of the dependence of log 2 K ( r ) on log 2 ( r ) for the surface after deformation (deformation 15 %) ( b )

Сравнительный анализ масштабно-инвариантых характеристик квазистатически нагруженных образцов позволил установить незначительное изменение показателя Хёрста H ~0,6 в широком диапазоне пространственных масштабов 4–110 мкм, что отражает универсальность сценария развития неустойчивого пластического течения между «критическими» точками. Анализ качественных различий в закономерностях скейлинга, соответствующих различным проявлениям «критичности» в окрестности критических точек по данным профилометрии, предполагает вычисление значений пространственных инвариантов (показателей Хёрста) с использованием данных атомно-силовой микроскопии, обеспечивающих более высокое пространственное разрешение флуктуаций рельефа в окрестности критических точек.

Заключение

В работе показано, что пластическое течение исследованного сплава обнаруживает многомасштабные признаки локализации пластической деформации на всём протяжении кривой пластического течения. Пластическая деформация протекает коррелированно по всему объёму образца с признаками вырождения структурных масштабов, характери- зующих размер зоны локализованного пластического течения и расстояния между ними. Анализ статистических распределений интервалов следования флуктуаций напряжений пластического течения установил существование двух критических точек, которые свидетельствуют о смене механизмов локализации пластической деформации. Первая критическая точка определяется значением деформации, соответствующим формированию множественных областей локализованной пластичности, с признаками автосолитонной динамики, обнаруживающим коррелированное поведение на макроскопическом размере образца. Переход через вторую критическую точку связан с качественным изменением типа коллективных мод в ансамблях дефектов [19]: переходом от автосолитонных мод, инициирующих локализацию пластического течения, к коллективным модам «обострения», формирующим очаги макроскопического разрушения.

Существование идентичных степенных негауссовых статистических распределений флуктуаций напряжений пластического течения в сплаве АМг6 [11] и флуктуаций момента при развитом турбулентном течении (течение Кармана) жидкостей [13, 14] позволяет предположить, что развитие неустойчивости пластического течения и турбулентного течения жидкостей при больших числах Рейнольдса соответствует механизмам переноса импульса в конденсированных средах, подчиняющихся одному «классу универсальности» [17, 30].

Полученные результаты потенциально имеют широкие и важные области приложений, в том числе при объяснении и моделировании эффектов локализованного (адиабатического) сдвига при динамическом и ударно-волновом нагружении широкого класса металлических материалов. Возможная универсальность природы развития неустойчивости конденсированных сред (твердых и жидких) при интенсивных воздействиях (в жидкостях – течения при больших числах Рейнольдса) представляет очевидный фундаментальный и прикладной интерес.

Работа выполнена при финансовой поддержке РФФИ (гранты № 16-48-590534, 17-01-00867).

Acknowledgments

The work has been carried out with the financial support of the Russian Foundation for Basic Research (Grant Nr. 16-48-590534, 17-01-00867).