Модели неупругого деформирования перекрестно армированных слоистых композитов

The поп-elastic stochastic boundary-value problem for a laminar composite with stochastic laminar arrangement are considered for the purpose of the composite nonlinear behavior calculation. The nonlinear constitutive functions for the composite layers are bound from the solution of some back boundary-value problem for the cross-angle laminar plastics. The calculated results are compared with experimental date.

Анализ нелинейного деформирования является актуальной задачей исследования механического поведения слоистых перекрестно армированных пластиков в связи с их широким применением в аэрокосмической технике. В ряде работ [1-5] рассматриваются способы прогнозирования неупругого поведения слоистых композитов на основе экспериментальных зависимостей для отдельного однонаправленного слоя при пяти способах нагружения: продольном расгяжении, продольном сжатии, поперечном растяжении, поперечном сжатии и сдвиге. С помощью различных методов указанные диаграммы деформирования аппроксимируются и используются для описания неупругого поведения всего слоистого композиционного материала. Однако такой способ расчета обладает и некоторыми недостатками, особенно в применении к перекрестно армированным композиционным материалам.

Во-первых, конструкция из такого композита , получаемая непрерывной намоткой армированной ленты, и его структурные элементы - однонаправленные слои - создаются одновременно в рамках единого технологического процесса. Поэтому, результаты экспериментов, проведенных на монослоях не точно описывают их реальное поведение в составе композита. Во-вторых, информации, которую можно извлечь из пяти вышеуказанных экспериментов для отдельного слоя, не достаточно для прогнозирования поведения при произвольном сложном напряженно-деформированном состоянии. По этим причинам для прогнозирования нелинейного поведения слоистых перекрестно армированных пластиков предлагается подход, основанный на использовании обратного решения сформулированной в [6] стохастической краевой задачи неупругого деформирования слоистого композита случайной структуры.

Рассмотрим краевую задачу для элементарного макрообьема композиционного материала со случайным расположением плоских анизотропных слоев, ортогональных оси Х3. При этом разнородные слои могут быть разориентированы на некоторый угол Будем считать, что на всех поверхностях раздела элементов структуры осуществляется идеальный контакт, те. выполняются условия [[UJ]-0 и [[о]3]] = 0, где [[а]] означает величину скачка функции а при переходе из одного слоя в другой, U -вектор структурных перемещений.

Уравнения равновесия содержат лишь по одному слагаемому, в котором дифференцирование проводится по переменной Х3:

ОУз — о , Ojg — < CJ13 > .

Угловые скобки означают операцию статистического осреднения, которая в рассматриваемом случае эквивалентна осреднению по объему.

Геометрические соотношения, устанавливающие связь структурных деформаций и перемещений, имеют вид :

Е ^ = < £ ц > + /2 (U (3^3 + U рб₁₃),                          (2)

где те

штрих означает пульсацию случайной величины (в данном случае перемещения), ее отклонения от математического ожидания.

Определяющие соотношения нелинейной среды [6];

£ ™ J Р ■ с ij J yinn

J ijmn 3 ijpq ( lpqmn - RpcrnnO ' ")),

где

J ijmn -тензор податливостей неупругого поведения , lpqmn - единичный тензор четвертого ранга, J уРЧ -тензор упругих податливостей, Rpqmn - тензор материальных функций поврежденного материала . Число независимых компонент и структура тензора Rp4nm зависят от анизотропии материала. Г® - инварианты тензора напряжений ( h=l, п ; п - число инвариантов). Уравнения (1) - (3) образуют замкнутую систему уравнений

Граничные условия

<оч

п j

Г “ Е 1

если задан вектор поверхностных сил S0 , эквивалентны заданию макронапряжений.

Соотношения (4) для ортотропных слоев композиционного материала в случае заданных макронапряжений при совпадении осей упругой симметрии с осями координат можно записать в следующем виде:

Е11“31111(1^+г|)СУц+]1122(1⁺ Г7) G22 + J1133 (1+ Г я) G33,

£ 22 = J221I (1+ г7) Оц + 12222(1"*" Г2) О22 "*" J2233 (1+ Г g) G33 ,

£ 33 = ЕзИ (1 + Г g) Оц + J 3322 (1+ Г д) G22 + ЪзЗЗ (1+ Г3 ) G33 ,

£ 23 = 2 J 2323 ( 1 + Г 4) G 23 ,

£ 1з = 2 lisa (1+ Гз) О 1з

£ 12= 2 J1212 (1+Г6) G12 .                                                             (6)

Очевидно, что независимые материальные функции неупругого поведения г, ( 1=1,..., 9 ) однозначно связаны с компонентами тензора R _pqmn для рассматриваемого материала.

Согласно теории малых упругопластических деформаций, предложенной Б.Е Победрей [7 ], для ортотропного тела аргументами материальных функций являются шесть инвариантов тензора напряжений;

= Oil ,              Iq^ = О₂₂ ,             1_О^(3> = Озз,

1СТ<4) = O44 ,               Ia(5) = о55 ,               Io(6) = G66                    (7)

Аналогично вводятся и инварианты тензора деформаций. Следует отметить, что инварианты тензоров напряжений и деформаций совпадают с компонентами этих тензоров только в системе координат, оси которой совпадают с главными осями ортотропии.

В работе [8] было показано, что стохастическая краевая задача неупругого деформирования слоистого композита с анизотропными слоями при заданных макронапряжениях <с_ч> сводится к системе п - Зп (п - число компонентов композита) нелинейных алгебраических уравнений относительно неизвестных пульсаций структурных величин.

В случае решения задачи в напряжениях разрешающая система уравнений будет выглядеть следующим образом:

Fi^(l> = (<Е и> - ^ш^СУ]^ - 1^Рц22^<СУ22^> - J* иггСУ 22 - ^нзз^<О'зз^> -

2 J¹ ni2^<CJi2^> -2 J^Pni2d i2)(J^Piih-) О ц=0 ,

Рз**’ = (< Е г??* " J^l^O)^ ~ ^пзгС) О - JP2222 - JI2233-

• -2 3^Р2212^<СУ12^> - 2 J^P2212C7 12 )( J¹ 222г) ' " СУ 22 “ 0 ,                                    (8)

Р*'1! = (<Е |2> ~ J^l^O)^ - JP]211C> П "J1 1222<О'22> " ^ГЗгзСУ 22"

-•1^Р1233^<Озз> - 2 У 1212^<CI12^> )( I* 1212) ’ " 20 12 ⁼ 0 , где

< Е ц> = < (У lllOOlp + j’ 1122 + JP1122O 22 + У 1133<Озз> +

2 J^Pni2^<Oi2^> + 2 J^P|U2O 12 )( J mi) '><( J^Pi 111) ¹ > ¹ = 0 ,

< E 22> = < (У2211<СУц> + JP1122O 11 + JP2222 + ^2233<Озз> +

2 J^P2212^<O12^> + 2 J^P2212O !2 )( У'зггг) ^ <( У’зТу) ’ > ‘ ~ 0 ,                 (9)

• < E 12-' ” < (J^P12H^<O11> + J^P1211O 11 + У 1222^<O22^> + ^12220 22 + У, 233^<O^33^> +

  2 J^P1212^<O12^>)( У1212) <( У1212) * ⁼ 0 .

Поскольку, в случае одноосного растяжения слоисто-волокнистого композиционного материала с различными углами армирования на уровне слоя обнаруживается сложное напряженно-деформированное состояние, зависящее от угла ориентации волокон в слое, то ряд экспериментов на одноосное растяжение образцов перекрестно армированного композита с разными углами укладки можно рассматривать как опыты для монослоя с реализацией различных напряженно-деформированных состояний . Результаты данных экспериментов можно использовать для построения нелинейных материальных функций монослоя и прогнозирования поведения всего композита при произвольных схемах нагружения .

В рассматриваемом нами случае нагружения перекрестно армированного слоистого пластика на структурном уровне реализуется плосконапряженное состояние, поэтому для решения системы ( 8 ) необходимо задать шесть материальных функций -(Г[, г₂, г₆, г₇, г₈, г₉), зависящих от трех инвариантов тензора напряжений . _П (О т (2) , (6К

Исследования многих авторов, проведенные для однонаправленных графитоэпоксидных материалов [1-5], дают основания предположить, что существенный вклад в нелинейность поведения перекрестно армированных композитов вносят напряжения сдвига , возникающие в слоях. Именно сдвиговые диаграммы деформирования в экспериментах на монослое носили наиболее нелинейный характер. С другой стороны, однонаправленные композиты, нагруженные вдоль волокон, также имели небольшое (порядка 10-15 %) отклонение диаграмм деформирования от линейности, причем конечный касательный модуль упругости в этом случае превышал начальный модуль, те. кривая носила слегка вогнутый характер.

Эти результаты, а также анализ экспериментальных диаграмм деформирования образцов перекрестно армированного композита с различными углами укладки ±6 при одноосном растяжении [ 9 ] послужили основанием для упрощения определяющих соотношений на структурном уровне. Предположим , что нелинейными являются только связи 1_£^(,)~1_О⁽¹⁾ и 1_£^<2)~1_ст^<2) , т е. г, = 0 при всех i, кроме 1 и 6. Будем также полагать, что указанные инварианты тензора деформаций зависят только от одноименных инвариантов тензора напряжений , т е. 1_£^||) = 1_£^(1>( 1_а^(|)) при i - 1 и 6. В этом случае неупругое деформирование слоя описывается двумя материальными функциями : ri(O'n) и г₆(О12 ) ■

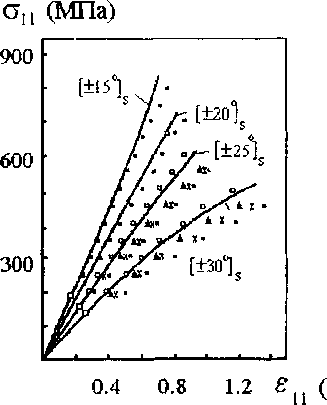
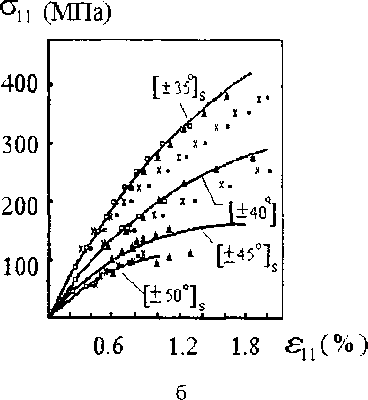
Рис 1 Сравнение экспериментальных (сплошная линия ) и расчетных данных для случая одноосного растяжения образцов углепластика с углами укладки (а) - ± 15, 20, 25, 30, (б) -35, 40, 45, 50". I X j 0 - расчетные данные моделей 1, 2, 3, 4 соответственно

За установочные эксперименты в модели 1 были приняты испытания на одноосное растяжение образцов слоистого пластика с углом армирования 0 °, поскольку эти испытания равносильны нагружению однонаправленного слоя, и такие же испытания для образцов с углом армирования ± 45 °, т.к. именно при этом угле армирования реализуются наибольшие деформации сдвига в слоях. В результате решения обратной задачи по данным этих экспериментов были получены и аппроксимированы кусочно-линейными зависимостями функции Г1(Оц) и г6(О12 ) Проверка адекватности модели осуществлялась на основе сравнения решений прямой задачи неупругого деформирования слоистых композитов [ 8 ] с экспериментальными данными по одноосному растяжению образцов углепластика с углами армирования ± 0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 60, 75, 90 ° [ 9 ] . При небольших углах укладки арматуры (0-15 ) значения структурных напряжений в слоях таковы, что нелинейное поведение слоя, а следовательно, и всего композита, определяется функцией гфоц) и введение ее в решение задачи приводит к хорошему совпадению экспериментальных и расчетных данных.При углах укладки от 20 до 50" Г|(Оц) на поведение материала влияния не оказывает и нелинейность материала определяется только материальной функцией Гб(О12) Однако при использовании в решении задачи зависимости , полученной на основе установочного эксперимента на одноосное растяжение образцов с углом укладки 45 °, было обнаружено большое (порядка 30 %) относительное отклонение расчетных и экспериментальных данных Результаты этого сравнения приведены на рис. 1 .

Диаграммы деформирования монослоя , соответствующие рассмотренной модели, показаны на рис.2. Для анализа зависимости функции г6(О|2 ) от угла армирования были решены обратные задачи по данным испытаний для образцов с другими углами укладки ( рис.З). Из рисунка видно, что все функции неупругого деформирования можно аппроксимировать тремя прямолинейными участками примерно с одинаковыми углами наклона (первый участок, когда r6(Oi2 ) = 0). Однако точки перехода от одного звена функции к другому соответствуют разным значениям сдвиговых напряжений для различных углов укладки. По-видимому, это обстоятельство указывает на то, что хотя функция г6 и является определяющей , все же нелинейное поведение слоя зависит и от других компонент тензора напряжений

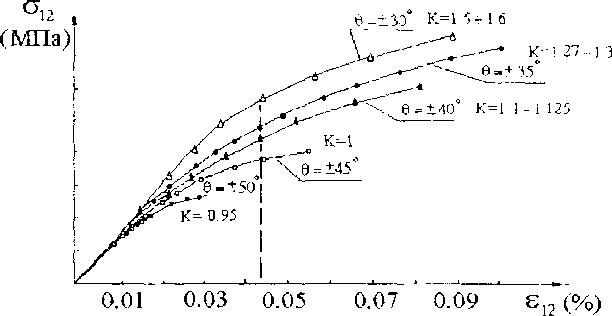
Рис 2. Диаграммы деформирования монослоя (из решения обратной задачи в соответствии с моделью 1)

Поэтому в моделях 2 и 3 на основе использования потенциала Мизеса [ 10 ] были последовательно введены две предельные поверхности пластичности вида :

AiC^n + BiCJ^ + CiCJ^Di , 1=1,2,                (10)

выход за границы которых определял тот или иной линейный участок функции неупругого поведения ( Dt=l , D2=7 ). Для определения шести коэффициентов , входящих в уравнения ( 10 ), использовались значения структурных напряжений, найденные из решения обратной задачи по данным трех установочных экспериментов для образцов с углами укладки ± 45, 40, 35 ".

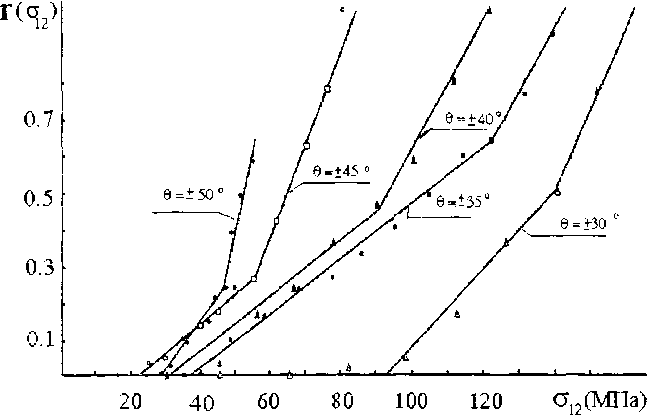
Рис 3. Функции неупругого деформирования г6 (Он ) для слоев с различными углами укладки (из решения обратной задачи в соответствии с моделью 1)

Таким образом , в модели 2 нелинейного поведения слоя материальная функция г₆ зависела от о_и и ст ₁₂, где сУы - значение напряжения сдвига , при котором выполняется условие (10), при i=l и функция г₆ принимает ненулевое значение .

В модели 3 функция г6 зависела от oi2 и сЛг (о"i2- значение напряжения сдвига, при котором выполняется условие ( 10 ) при i =2 и функция неупругого деформирования начинает описываться третьим аппроксимирующим звеном) . Относительное отклонение экспериментальных и расчетных данных уменьшилось до 20% при использовании модели 2 нелинейного поведения слоя, а при использовании модели 3 составило примерно 15 % ( см, рис 1 ).

В модели 4 неупругого поведения материала слоя был использован показатель напряженного состояния слоя К = 2О|2/ Оц +о22 В слоях перекрестно армированных пластиков с углом армирования 45 ‘ это отношение равно 1. Для композитов с меньшим, чем 45" углом армирования К > 1 Для образцов с большими углами укладки К < 1 (см. рис.2). Материальная функция неупругого поведения r6(Oi2 ), полученная из экспериментальной кривой для образцов с углом укладки 45 , была принята за основную, а материальные функции композитов с другими углами укладки вычислялись по формуле:

Гб = Гб(О12) ,45° - а(к |).                                (11)

Для определения константы а необходимо использовать данные еще, как минимум, одного эксперимента в дополнение к опыту по растяжению образца с углом армирования 45 ‘. Относительное отклонение экспериментальных и расчетных данных в случае использования модели 4 неупругого поведения слоя не превышало 5% . Таким образом, модель, основанная на введении параметра напряженно-деформированного состояния в функцию неупругого поведения , связывающую структурные деформации и напряжения сдвига , позволяет при минимальном количестве установочных экспериментов адекватно описывать процессы неупругого деформирования однонаправленного слоя и прогнозировать нелинейное поведение слоистого композита при произвольных углах армирования.