Модели оценки энтропии в экономике

Энтропи́я (от др.-греч. ἐντροπία — поворот, превращение) — широко используемый в естественных и точных науках термин. Впервые введён в рамках термодинамики как функция состояния термодинамической системы, определяющая меру необратимого рассеивания энергии. Кроме физики, термин широко употребляется в математике: теории информации и математической статистике. Энтропия может интерпретироваться как мера неопределённости (неупорядоченности) некоторой системы. Другой интерпретацией этого понятия является информационная ёмкость системы. С данной интерпретацией связан тот факт, что создатель понятия энтропии в теории информации Клод Шеннон сначала хотел назвать эту величину информацией. В широком смысле, в каком слово часто употребляется в быту, энтропия означает меру неупорядоченности системы; чем меньше элементы системы подчинены какому-либо порядку, тем выше энтропия.

Оказалось чрезвычайно удобным объяснять научно непредвиденные аномалии социально-экономического развития влиянием энтропии. То есть задуманное не получилось потому, что система оказалась "неупорядоченной", недостаточно информативной, распыленной, чрезмерно демократичной и т.д., в общем – плохая энтропия. Понятие энтропии в экономике сформулировано весьма расплывчато, не имеет четкого определения, например:

"Энтропия в экономике – это количественный показатель беспорядка, мера излишней работы при достижении поставленной цели, доля неполезных побочных процессов или явлений, сопровождающих какую-либо деятельность" [2].

Энтропийный закон в замкнутой экономической системе характеризует меру хозяйственного порядка-беспорядка за временной цикл взаимодействия через реализуемые стабильные и дестабилизированные режимы экономического обмена.

При определении энтропии в экономике, согласно представленной модели, получаем сложную зависимость взаимодействия элементов процесса, в том числе человеческой деятельности. Поэтому простое суммирование или какое-либо усреднение энтропий элементов процесса не может быть корректным. Необходимо оценивать взаимосвязи в системе, функциональные зависимости процессов жизненного цикла, Управления и Механизма, что порождает более сложные логические и математические взаимосвязи.

Энтропия характеризует функционирование системы.

• -    S -многомерная случайная величина Y = (Y Y 2 ,.., Y m )

• -    Если случайный вектор Y имеет многомерное нормальное распределение, то H ( Y ) = m^H ( Y ) + 1ln|R|

1= 1          2

Существуют две модели энтропии в экономике.

• 1.Энтропийно-вероятностная модель . Данная модель позволяет выделить элементы сложной системы и связи между ними в качестве отдельных переменных . Система и ее составляющие изображены на

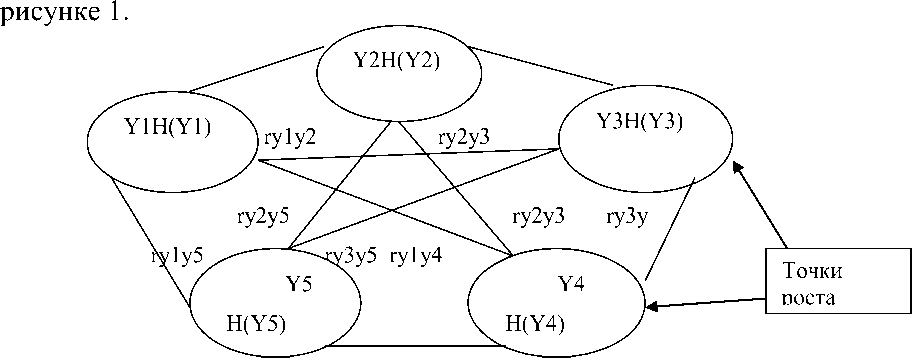
Рис. 1 Система и составляющие энтропийно-вероятностной модели

Утверждение 1 . Пусть X 1 , X 2 – две непрерывные случайные величины с конечными дисперсиями, определенные на всей числовой оси, и

>2

описываемые однотипными распределениями. Тогда H (X2) -H(X1)= In —

= Я.Ц , 512,^22,^1Д2 — дисперсии и параметры масштаба случайных величин X1 и X2.

Утверждение 2. Пусть имеем две системы непрерывных случайных величин

Y(1) =( y(1),Y2(1),....,Ym(1)  ) и Y(2^=  (Y1(2\Y2(2\....,Ym(2). Тогда разность совместных энтропий систем случайных величин равна:

AH(Y) = H(Y(2))-H(Y(1)) = £in "   +1 £ l< R, где

k = 1     ^ _Y (1)     ² k = 2      ¹    R _Y (1) / ^ (1) . _Y (1)

¹ R ( j )   ( j )    ( j )

^Yk ' ^Y 1     .. ^{- Y}k -1

^ v (Л_/У( Л И » = ^ v ( j )

^Yk ' ^Y 1    ^-.^{- Y}k -1             ^Yk

D 2

R ( j )/y( j )    ( j )

^Yk   ^1Y 1    "’^Yk - 1

- коэффициенты детерминации соответствующих зависимостей k = 2,3,

1 m^,   ^{1    R} Y ⁽²⁾ /Y ⁽²⁾ ... Y ,⁽²2

...,

m j = 1,2 . Обозначив     A H ( V )_R = - 2^ in---- k —¹— k-^ представим

2 k = 2    1 - R^/ y _(1M 1

систему как  AH (Y) = AH (Y)E +AH (Y)R, где  AH (Y)s, AH (Y)R -приращения энтропии за счет изменений дисперсий и корреляций случайных величин 2. Энтропийно-динамическая модель. В основе практического применения энтропийно-динамической модели в экономике лежат следующие идеи:

• -    гипотеза: Поведение системы можно считать стохастическим

• -    формирование системы признаков с помощью факторного анализа

• -    мониторинг состояния системы в динамике (анализ изменения энтропии)

Отсюда можно сделать такие выводы, что в основе энтропийного моделирования динамики стохастических систем лежит представление системы в виде случайного вектора, каждая из компонент которого представляет собой непрерывную случайную величину. Данный подход позволяет решать задачи мониторинга состояния стохастических систем в экономике.