Модели подкрепленного стыка двух тонкостенных цилиндров разной толщины

Обращение к решению осесимметричной задачи теории оболочек связано с применением новых материалов и разнообразием подобных конструкций в авиационной, ракетно-космической технике, подводном флоте, химическом машиностроении и др. Различные задачи для подобных конструкций рассматриваются в многочисленных современных работах, например [1, 2, 3, 4, 5, 6].

Рассмотрим напряженное состояние (НС) цилиндрической оболочки, представляющей конструкцию из двух последовательно состыкованных полуоболочек разной толщины. Место стыка подкреплено шпангоутом (рис. 1). Оболочка загружена внутренним давлением.

Расчеты подобных оболочечных конструкций в проектных организациях хорошо согласуются с зависимостями классической теории оболочек с тонкостенностью R / 3 >  100 ( R — радиус срединной поверхности, 3 - толщина оболочки). По расчетам более “толстых” оболочек мнение различных исследователей (см. материалы съездов и симпозиумов по теории оболочек) не однозначны.

В работе оценивается правомерность применения зависимости теории оболочек при тонко-стенности 30-70 путем сравнения результатов расчета и эксперимента.

Объектом расчета и испытания была спроектированная авторами точеная оболочка из ста-

ли-3 со скачкообразным изменением толщины с усилением в виде шпангоута прямоугольного сечения (рис. 1) в середине длины оболочки. Толщина “первой” полуоболочки 3 1 = 0,135 см, второй - З 2 = 0,255 см при радиусе внутренней поверхности R = 8,38 см; ( R/3 ) 1 = 62,6 ; ( R / 3 )₂ = 33,4 .

НС оболочек вдали от стыка описывается формулами безмоментной теории оболочек [7, 8]:

R „ R pR ²

Г 0 = Р^ ; ³ о = Р^ ; w = — , (1) 2 3         3        E3

где Г , p , E - напряжение, давление, модуль упругости; w ₀ - радиальные перемещения считаются положительными при увеличении радиуса оболочки. Индексы “ x ” и “ ф ” соответствуют осевым и кольцевым напряжениям.

Вблизи стыка оболочек картину НС можно получить из решения краевой задачи, учитывающей изгиб образующих для каждой полуоболочки:

d ⁴ w i dx i⁴

+ 4 k i ⁴ w i = 0 , k i ⁴

3(1 - д ²) R_l²3₁²

где i – номер полуоболочки, w – радиальные перемещения, Д - коэффициент Пуассона.

Место стыка можно представить двумя моделями (рис. 2). Системы отсчёта продольных координат x i для левой и правой полуоболочек обозначены соответственно х 1 и x ₂ . Для первой модели (рис. 2а) площадь шпангоута обозначена f 1 , для второй модели (рис. 2б) - f ₂ .

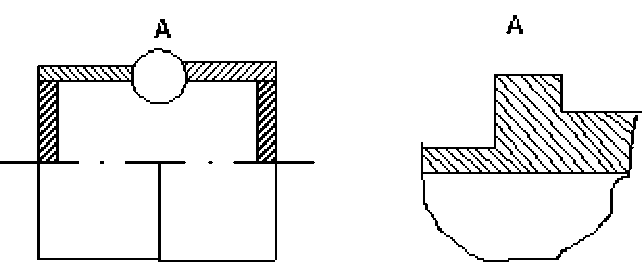
Рис 1. Схема оболочки со шпангоутом

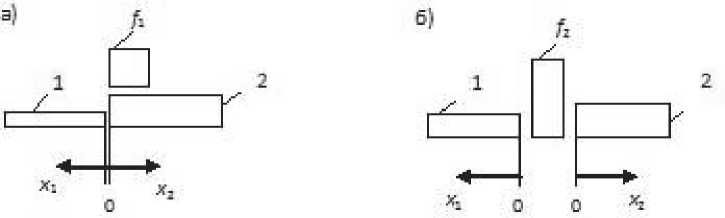
Рис. 2. Расчетные модели стыка оболочки: f – площадь шпангоута, 1 - левая полуоболочка, 2- правая полуоболочка, 0 – начало систем отсчета

Решая задачу в физически и геометрически линейной постановке, НС получим суммированием результатов расчета оболочек отдельно от действия внутреннего давления (1) и действия погонных краевых нагрузок Q i и m i , если Q – поперечная сила, m – изгибающий момент, положительные направления которых показаны на рис. 3.

Решение дифференциального уравнения (2) запишем форме [8] и воспользуемся методом [7]. Суть метода заключается в разделении НС на основное и дополнительное. Здесь в качестве основного принято безмоментное состояние оболочки, без учета возмущений от шпангоутов и днищ. Индексы “0” в обозначениях напряжений и перемещений характеризуют это состояние. НС от местных возмущений считается дополнительным и соответствует решению краевой задачи теории оболочек.

Такой подход упрощает решения и делает их более наглядным при анализе результатов расчета. Он позволяет получить аналитические выражения для расчета перемещений и напряжений в виде (здесь и далее индексы i для первой и второй полуоболочек опустим):

w = 1 + 2[ m у ( kx ) + Q O ( kx )] ;

У ф = w ± I ^{6 A} , [ m Ф ( kx ) + Q f (kx )] ;

A 3(1 - A ²)

ox = ^x°- ±     6     [ m ф (kx) + Q f (kx)] , оф о   -V 3(1 — a 2)

_ k2 k w _ % _ m = —mо; Q = —Qо; w =— ; аф = ^-; ox p          p w о Уф 0

^o x

,

^У 0

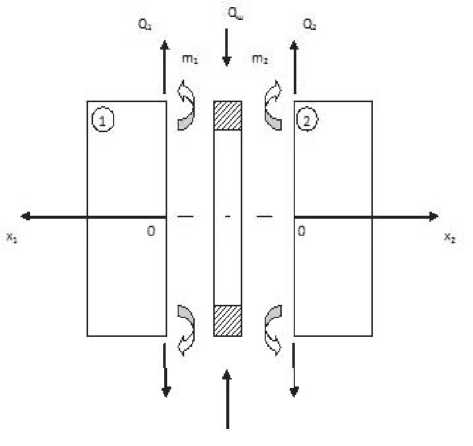
Рис. 3. Схема краевых нагрузок для исследуемой конструкции

где m ₀, Q ₀ , у ( kx ), O ( kx ), ф ( kx ), f ( kx ) - краевые нагрузки в сечении x = 0 и функции Тимошенко, значения который затабулированы в [8]. Аналитические выражения m о и Q о для ряда схем оболочек приведены в [9].

Величины w и о показывают, во сколько раз действительные перемещения и напряжения отличаются от вычисленных по безмоментной теории оболочек. Знак “+” в (3) относится к внутренней, знак “-” – к наружной поверхности оболочки.

Теоретической основой расчета служили зависимости [9], полученные на базе моментной теории оболочек. Эксцентриситет срединных поверхностей при расчетах не учитывался. Предполагая, что сечение шпангоута не сопротивляется кручению, получим m₁ = m 2 = m 0 . В этом случае, шпангоут загружен только силой ^Qш = ^{- (} Q 1 ⁺ Q 2 ) .

Для рассматриваемой конструкции зависимости [9] для расчета краевых нагрузок при одинаковых модулях упругости левой и правой полуоболочек ( E i = E 2 = E ) принимают следующий вид:

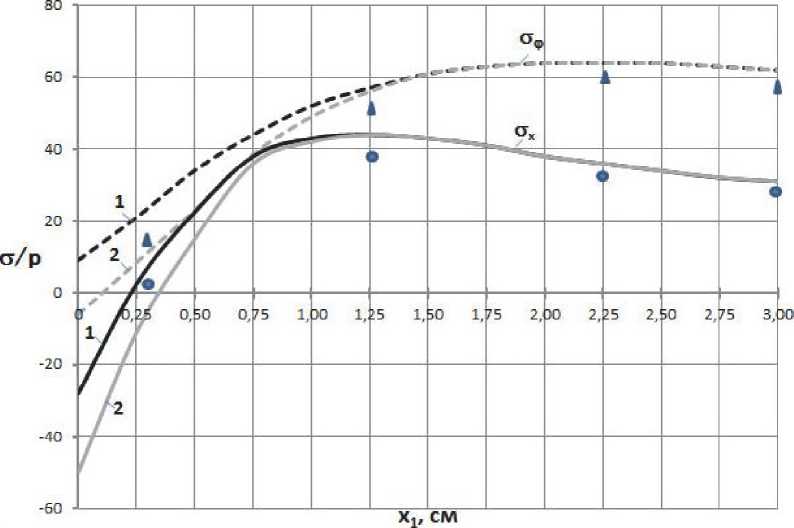
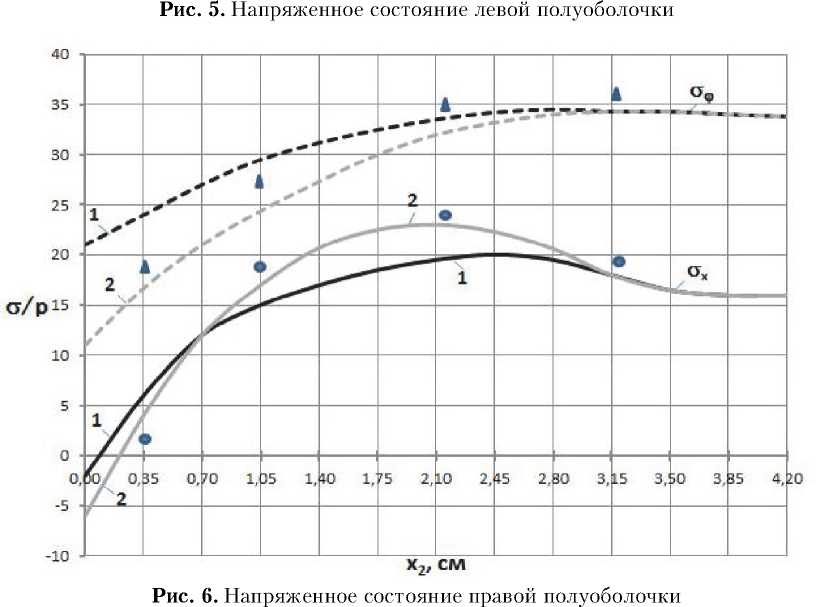
p = 1 МПа приведены на рис. 5 и 6 соответственно. Кривые, соответствующие первой и второй расчетным моделям, обозначены номерами 1 и 2.

Связь между координатами x ₁, x ₂ и безразмерными координатами k i x i , необходимыми для вычисления значения функций Тимошенко, приведена в табл. 1.

0,85

0,85 _T , f

Q i = ^- P"^ 1 L ⁺ k 2^T 5 ₂

k1M

2+C 512 Ci + 5

V 5 2 J V 5 2,

h,

n    085 t t f

Q 2 = p .^ 1 L ^- k;

k 1 M      ⁵

0,85

k1M

5 J1 + C5 J1 . 52 J V 5i J

V

i + 2 C ⁵ J²

V ⁵ 2 J

J

h,

m ₀

^^^^^s

0,425 L

P^ ll 1 k1 M V

^^^^^s

5J2 . 52J

-1

+ 2 kf

2 52

1 * C8512

V 52 J

h,

Экспериментальная часть исследования напряженного состояния конструкции выполнялась классическим методом тензометрирования. Схема экспериментальной установки представлена на рис. 4.

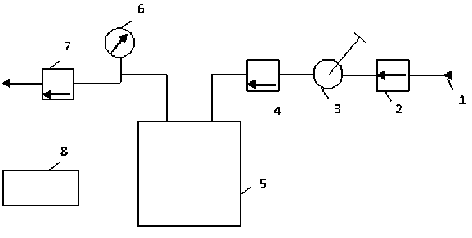
Рис. 4. Схема экспериментальной установки

m . 1+C 5 у + 2C 5 12V52 J    V 52 J

1 + ⁵ + C ^ LJ ²

⁵ 2 V ⁵ 2 J

+ 2 k₂f

² 5 2

1 +1 5 -12

V 5 2 J

Для рассматриваемой конструкции коэффициенты дифференциальных уравнений (2) равны соответственно k ₁ = 1,203 см ^{- 1} , k 2 = 0,872 см ^{- 1} . Длина оболочки, равная 26 см, обеспечила для каждой полуоболочки условие, предложенное в [8]: kl >  6 - условие отсутствия влияния жестких днищ на напряженное состояние в ее середине. Краевые поперечные силы Q ₁ и Q ₂ , рассчитанные по формулам (4), оказались отрицательными, а изгибающий момент m ₀ – положительным.

Напряжения на наружной поверхности конструкции рассчитывались по формулам (3) при двух расчетных моделях (рис. 2). Первой модели (рис. 2а) соответствовала площадь шпангоута f ₁ = 0,224 см², второй (рис. 2б) – f ₂ = 0,479 см². Результаты расчетов для левой (первой) и правой полуоболочек при внутреннем давлении

Внутреннее давление обеспечивалось напором воды, забираемой из водопровода 1 через вентиль 2. Ручной насос 3 позволял создавать при открытом вентиле заполнения 4 внутри испытуемой оболочки 5 давление до 2,5 Мпа, которое контролировалось манометром 6. Давление из оболочки сбрасывалось вентилем дренажа 7 .В качестве тензостанции 8 использовались два усилителя 8АНЧ со специально разработанной коммутационной и измерительной аппаратурой.

Тензодатчики с пятимиллиметровой базой наклеивались на наружную поверхность оболочки в виде прямоугольной розетки. Оси чувствительности датчиков располагались вдоль образующей и перпендикулярно ей. Розетки располагались по двум диаметрально противоположным образующим.

В опытах измерялись относительные деформации E x и Е ф , которые осреднялись по показаниям датчиков диаметрально противоположных розеток в одном поперечном сечении оболочки. По относительным деформациям вычислялись напряжения

Таблица 1. Связь между безразмерными и размерными координатами

x 1 , см	0,5	1,0	1,5	2,0	2,5	3,0
x 2 , см	0,7	1,4	2,1	2,8	3,5	4,2
k 1 x 1 = k 2 x 2	0,6	1,2	1,8	2,4	3,0	3,6

° Ф = ^ Г ( ^ ф + ЦЕ х }

1 - Ц 2

^х _     Г(ех + Ц£ф}.       (5)

Сравнение результатов расчета с результатами опыта свидетельствует об их вполне удовлетворительном совпадении, т.е. о правомерности использования формул [9] в расчетной практике, так как различие в напряжениях, полученных расчетом и экспериментом, в зонах возмущения не превысило 11 %. Зона возмущений носит более локальный характер для оболочек меньшей толщины. Область возмущений в первой оболочке оказалась ограниченной параметром kiXi < 2,5 , во второй - k2X2 < 3. Следовательно, область возмущений в осесимметричной задаче можно ограничить величиной параметра kl < 3.

Вторая модель стыка, предполагающая большее значение площади шпангоута и вызывающая большее возмущение полей напряжений, является предпочтительной.

Расчеты напряженного состояния по предложенным зависимостям дают более высокие значения напряжений чем результаты опыта, что идет в запас прочности.

• 1.    Актуальные проблемы механики оболочек // Труды Международной конференции. Казань, 26 - 30 июня 2000 г. Казань: Новое Знание, 2000. 488 с.

• 2.    Антоненко Э.В., Шульга Т.Э. Математические модели потери устойчивости неоднородных цилиндрических оболочек от неравномерной радиальной нагрузки // Изв. Сарат. ун-та. Нов. сер. Сер. Математика. Механика. Информатика. 2009. Т. 9. Вып. 3. С. 79–83.

• 3.    Джашитов В.Э., Панкратов В.М., Барулина М.А.

• 4.    Крысько В.А., Жигалов М.В., Яковлева Т.В., Крылова Е.Ю., Папкова И.В. Метод установления в нелинейных задачах балок и пластин с учетом локальности нагружения // Вестник Саратовского государственного технического университета. 2012. Т. 2. № 1. С. 7–17.

• 5.    Теории оболочек и мембран в механике и биологии: от макро- до наноразмерных структур = Shell and Membrane Theories in Mechanics and Biology : from Macro- to Nanoscale Structures: материалы междунар. науч. конф. / Минск, Беларусь [под общ. ред. Г.И. Михасева, X. Альтенбаха]. Минск: Изд. центр БГУ, 2013. 295 с.

• 6.    Торопова О.А. Математическое описание напряженно-деформированного состояния райзера, выполненного из нелинейно-упругого материала // Вестник Саратовского государственного технического университета. 2012. Т. 1. №2(64). С. 36–41.

• 7.    Кан С.Н. Строительная механика оболочек. М.: Машиностроение, 1966. 508 с.

• 8.    Тимошенко С.П., Войновский-Кригер С. Пластинки и оболочки. М.: Физматгиз, 1963. 636 с.

• 9.    Антоненко Э.В. Расчет сопряженных оболочек, выполненных из неодинаковых материалов разной толщины // Проблемы прочности. 1973. №6. C. 90-96.