Модели сценарного изменения итоговых показателей баланса

В настоящее время существует проблема выбора сценарного метода прогнозирования баланса. Однако не менее сложной является проблема предвидения предстоящего кризиса и своевременной минимизации его последствий. Большинство современных организаций, начиная с момента своего возникновения, сталкиваются с целым рядом проблем, которые могут спровоцировать острый кризис, сопровождающийся резким ухудшением показателей деятельности: ликвидности, платежеспособности, рентабельности, оборачиваемости оборотных средств, финансовой устойчивости.

Для своевременного выявления, локализации и предотвращения рисков и угроз необходимо использовать и применять те методы, которые позволяли бы одновременно учитывать тенденции развития организации в ретроспективной оценке, осуществлять отбор факторов управления и контроля для целевого воздействия и контроля изменения значений показателей, формировать альтернативные варианты прогнозов с целью роста эффективности и результативности деятельности, рассчитывать и анализировать допустимые значения (прогнозные ожидания показателей), которые выступают индикаторами для выявления угрозы банкротства [4].

В рамках данной статьи рассмотрены некоторые методы сценарного планирования, такие как методы экстраполяции (метод скользящей средней, метод наименьших квадратов, экспоненциального сглаживания), а также графическая модель поиска структурных соотношений показателей баланса О.В. Вишневской.

Рассмотрим более подробно метод скользящей средней и метод графической модели О.В. Вишневской (рис.1).

Графическая модель поиска антикризисных структурных соотношений баланса О.В. Вишневской показателей баланса.

Б

Б

Б

Б

СК

Б

ВНА Б

ВНА

Б

Основан на установлении координат точек отчетной финансовой устойчивости «У» и отчетной текущей ликвидности «Л» на графике с баланса, а также поиске новых точек, отвечающих оптимальным соотношениям

СК +ДО

Б Б

ДО^ ко

+ и пассива

Б Б

^= 100 о

= 100 Б

Виз W"1»1^

Б Б Б

ВНА + ЗиЗ Б

Основан на предположении, что следующий по времени показатель по своей величине равен средней, рассчитанной за последние 3 периода.

_п _ Л_о_₁+/7_о_₂⁺ Ло-з

' '0+1               о

Рассматриваемые мето ды ф ор мир о в ания прогнозного баланса

Метод скользящей средней wwww>A^v •■-■-■-■---■-■-■-■---■-■-■-■---%-■-■-■-. •■-^-----х--v----------.

Рисунок 1 — Методы формирования прогнозного баланса

Особенностью метода скользящей средней является возможность выравнивать динамический ряд на основе его средних характеристик. Метод дает прогнозную точечную оценку и более эффективно используется при краткосрочном прогнозировании [1]. Применение метода скользящей средней дает возможность исключать случайные колебания и получить значения, которые соответствуют влиянию главных факторов. Сглаживание достигается путем взаимного погашения случайных отклонений в рамках рассчитанных средних значений. Чем шире интервал сглаживания, тем более плавным получается тренд [3].

Графическая модель структурных соотношений баланса О.В. Вишневской помимо отчетной ситуации дает возможность построить желательную структурную ситуацию, отвечающую требованиям оптимальности и антикризисности. Она особенно эффективна в графическом исполнении, когда текущие значения показателей сравниваются с критическими и появляется возможность наглядного представления путей изменения структуры баланса в сторону его антикризисных значений. Однако это требует применения координационной сетки, в которой координатные оси представлены удельными значениями основных статей актива и пассива бухгалтерского баланса [5].

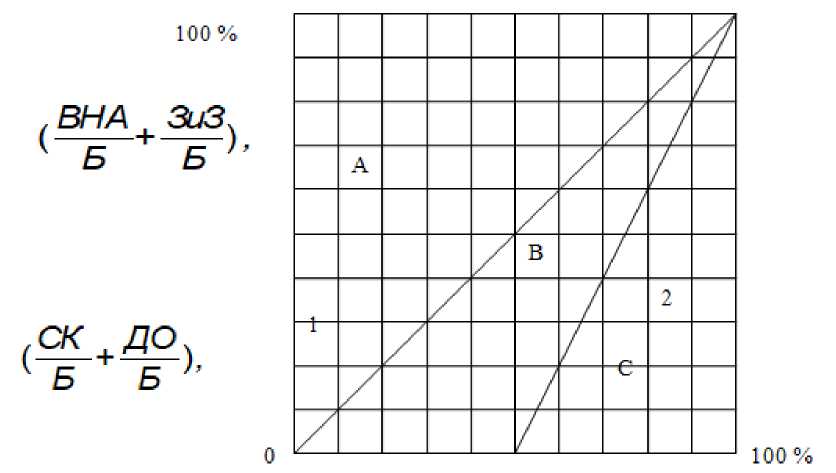
Рисунок 2 — Графическая модель поиска антикризисных соотношений элементов структуры имущества и его источников

Графическая модель построена в координатах, отражающих по два основных структурных элементов имущества (удельный вес внеоборотных активов ВНА и удельный вес запасов и затрат ЗиЗ) и структурных элементов его ББ источников (удельный вес собственного капитала СК и удельный вес долгосрочных обязательств ДО).

Линия 1 построена по уравнению (СК) = (ВНА + ЗиЗ), отражающему условие

абсолютной

финансовой

устойчивости

СК-ВНА

Дсос=1ит-=1-

Линия 1 делит поле графической модели на две области: область А – финансовой неустойчивости и область (В + С) - финансовой устойчивости.

Линия 2 построена по уравнению [ ВНА = 2 ( СК + ДО ) - 1 ], отражающему Б   ББ

ОА    Б-ВНА условие достаточности текущей ликвидности Ктл = — = Б_(-ск+Д0-) = 2.

Линия 2 делит поле графической модели также на две области: область (А + В) - недостаточной текущей ликвидности (Ктл < 2) и область С -достаточной текущей ликвидности (Ктл > 2).

Текущее значение финансовой устойчивости предприятия выражается на графике точкой пересечения значений (— + ЗиЗ) и СК, взятых из ББ   Б бухгалтерского отчета предприятия на текущий момент.

Текущее значение ликвидность предприятия выражается на графике точкой пересечения значений ( ВНА ) и ( СК + ДО ) , также взятых из бухгалтерского отчета предприятия на текущий момент.

Расположение точек финансовой устойчивости и текущей ликвидности относительно пороговых линий 1 и 2 характеризует текущее состояние и направления изменений существующих структурных соотношений ВНА, ЗиЗ СК

Б ^, Б ^,

ДО

Y в сторону

достижения желаемых антикризисных значений, соответствующих ликвидности [2].

областям финансовой устойчивости и достаточной

1 проведем сравнительную характеристику методов

В таблице скользящей средней и графической модели поиска структурных соотношений показателей баланса О.В.Вишневской, выделим их основные достоинства и недостатки.

Таблица 1 — Сравнительная характеристика метода скользящей средней и графической модели поиска структурных соотношений показателей баланса О.В. Вишневской

Метод скользящей средней	Графическая модель поиска структурных соотношений показателей баланса О.В. Вишневской
Достоинства:
1. Наименее трудоемкий	1. Дает наглядную картину структурной ситуации баланса и уровня финансового состояния
2. Прост в вычислениях	2. Возможность построения желательной структурной ситуации, отвечающей требованиям оптимальности и антикризисности
	3. Возможность абстрагирования от абсолютных числовых значений статей баланса
	4. Возможность сравнения на одном графике несколько предприятий
Недостатки:
1. Не дает точных результатов на длительный срок прогноза	1. Наиболее трудоемкий
2. Рассматривается в краткосрочном периоде
3. Ошибки прошлых лет автоматически переносятся на прогнозный период
4.   Невозможность  учета  влияния случайных факторов

На основании вышеизложенного можно сделать вывод о том, что выбор метода планирования прежде всего зависит от целей и задач организации, от ее специфики. Однако применение графической модели поиска структурных соотношений показателей баланса О.В. Вишневской является беспроигрышным вариантом для любой фирмы.