Модели систем квазипериодических процессов на основе цилиндрических и круговых изображений
Автор: Крашенинников В.Р., Кувайскова Ю.Е., Маленова О.Е., Субботин А.Ю.
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Информатика, вычислительная техника и управление
Статья в выпуске: 1 т.23, 2021 года.
Бесплатный доступ
Поведение объектов во многих практических ситуациях имеет квазипериодический характер - наличие заметной периодичности со случайными вариациями квазипериодов. Например, шум и вибрация авиационного двигателя, гидроагрегата, сезонные и суточные колебания температуры атмосферы и т.д. При этом у объекта может быть несколько параметров, поэтому объект описывается системой нескольких временных рядов, то есть нескольких случайных процессов. Возникающие задачи мониторинга (оценивания состояния объекта и его прогноз) требуют задания модели такой системы процессов и ее идентификации для конкретного объекта по результатам его наблюдений. В данной работе для представления квазипериодического процесса применяется авторегрессионная модель в виде разверток нескольких цилиндрических или круговых изображений по спирали. Сначала моделируются «стандартные» независимые между собой процессы с нулевым средним и единичной дисперсией и заданными корреляциями внутри периодов и между ними. Заданные дисперсии и корреляции процессов системы достигаются соответствующим линейным преобразованием системы стандартных процессов. Выбирая значения небольшого количества параметров этой модели, можно описывать и имитировать широкий класс систем квазипериодических процессов с учетом корреляций внутри квазипериодов, между ними и между процессами системы. Рассматривается задача идентификации модели, то есть определения значений ее параметров, при которых она в определенном смысле наилучшим образом соответствует реально наблюдаемому процессу. Эта задача решается с помощью псевдоградиентной адаптивной процедуры, которая осуществляет рекуррентную настройку параметров модели в порядке поступления наблюдений реального процесса. Эта процедура сходится к точным значениям параметров в случае однородных временных рядов, а в случае неоднородных оценивает изменяющиеся со временем параметры. Преимуществом этой процедуры является возможность функционирования в реальном времени с небольшими вычислительными затратами. Приведены примеры имитации систем временных рядов.
Система квазипериодических случайных процессов, модель, авторегрессия, цилиндрическое изображение, идентификация модели
Короткий адрес: https://sciup.org/148314255
IDR: 148314255 | УДК: 621.391(075) | DOI: 10.37313/1990-5378-2021-23-1-103-110
Текст научной статьи Модели систем квазипериодических процессов на основе цилиндрических и круговых изображений
Поведение многих технических, экономических, биологических и других объектов описывается множеством параметров. Эти параметры регистрируются через определенные моменты времени, что образует систему вре- Крашенинников Виктор Ростиславович, доктор технических наук, профессор, заведующий кафедрой «Прикладная математика и информатика».
менных рядов. Имеется обширная литература по теории представления и обработки временных рядов или случайных процессов, например, монографии [1-5].
Часто в динамике контролируемых показателей объекта наблюдается нерегулярная периодичность – квазипериодичность. Квази-периодическое поведение есть повторения с компонентом непредсказуемости, не поддающимся точному прогнозу. Например, вибрация различных двигателей и турбин, биоритмы, суточные колебания температуры и тому подобное [6]. Для описания квазипериодических процессов используются различные способы, например, введение гармонических составляющих в явном виде со случайными амплитудами или применение авторегрессионных моделей с комплексными корнями характеристического уравнения. В [7-9] для описания квазипериоди- ческих процессов предложено использование авторегрессионных моделей на цилиндре. Эта модель при подходящем выборе ее параметров дает возможность описывать и имитировать широкий класс квазипериодических процессов, в том числе нестационарных. В настоящей работе рассматриваются модели систем ква-зипериодических процессов в виде изображений, определенных на многослойных (или толстостенных) цилиндрах. Каждый из этих слоев соответствует одному из процессов системы. Корреляции между процессами определяются «внешним» уравнением авторегрессии, что позволяет задавать широкий класс различных зависимостей между этими процессами.
Для адекватного описания конкретной наблюдаемой системы временных рядов, предположительно описываемой некоторой моделью рассматриваемого вида, возникает задача идентификации этой модели, то есть нахождения значений ее параметров, при которых модель реализует систему квазипериодических процессов, максимально приближенную по своим свойствам к наблюдаемой системе временных рядов. Эту задачу предлагается решать с помощью псевдоградиентной адаптивной процедуры.
В работе приведены примеры моделирования систем временных рядов с помощью предложенных моделей.
АВТОРЕГРЕССИОННЫЕ МОДЕЛИ НА ЦИЛИНДРАХ И КРУГАХ
Для описания квазипериодических процессов используются различные способы, например, введение гармонических составляющих в явном виде или применение авторегрессионных моделей с комплексными корнями характеристического уравнения. В данной работе будет применено представление таких процессов с помощью изображений. Характерной особенностью квазипериодического процесса (сигнала) является его двойная коррелированность: имеется высокая корреляция как между соседними отсчетами, так и между отсчетами, отсто- ящими на несколько периодов. Такое свойство имеют различные изображения, описываемые плоскими случайными полями: отсчеты кор-релированы и вдоль строк, и вдоль столбцов. Поэтому можно было бы представить квази-периодический сигнал в виде построчной развертки изображения. Однако при этом конечная точка строки будет приставлена к начальной точке следующей строки. Но на исходном изображении эти точки находятся на большом расстоянии друг от друга, поэтому на этих стыках развернутый сигнал будет иметь очень малую корреляцию, несвойственную реальным квази-периодическим процессам.
Коррелированность сигнала на стыках соседних периодов можно получить следующим образом. Рассмотрим цилиндрическое изображение, например, изображение вала вращения. Если его разрезать вдоль и развернуть в плоскость, то оно превращается в прямоугольное изображение. На исходном цилиндрическом изображении точки вдоль линии разреза были рядом, поэтому отсчеты в них сильно корре-лированы и сигнал в виде последовательности строк этого разрезанного изображения будет иметь характерные свойства квазипериодиче-ского изображения.
Для построения модели цилиндрического изображения рассмотрим спиралевидную сетку на цилиндре, показанную на рис. 1a. Строки этой сетки представляют собой витки спирали (винтовой линии). Тогда изображение может рассматриваться как одна последовательность отсчетов вдоль этой спирали, что очень удобно для авторегрессионного представления. Рассмотрим, например, аналог авторегрессионной модели Хабиби [8-10]:
x k , i = ^ x k , i - 1 + r x k - 1, i - ^ r x k - 1, i - i + q ^ k , i , (1) где k – номер витка спирали; l – номер узла в витке; s и r – параметры модели; x k , l – независимые ст андар тные случайные величины; при этом i = 0, T - 1 ; xk l = xk+ 1 -T при I > T ; T - период, то есть количество точек в одном витке. Для использования (1) значения на первом витке
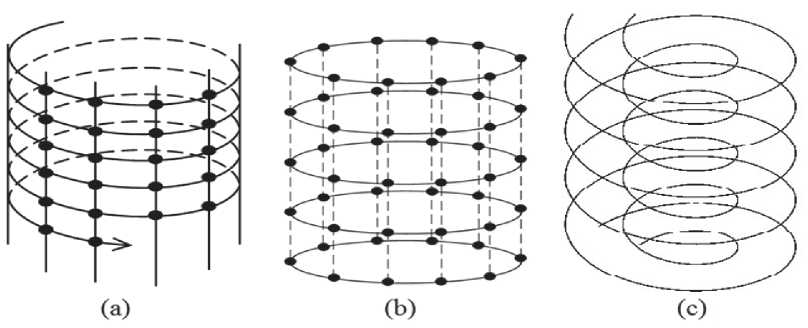
Рис. 1. Сетки: (a) на спирали; (b) на системе окружностей; (c) на системе цилиндров
должны быть заданы отдельно. Отметим, что в модели (1) сетка может рассматриваться и как обычная цилиндрическая (в цилиндрической системе координат), то есть как последовательность окружностей (рис. 1b).
Полученная модель цилиндрического изображения может быть представлена в эквивалентном виде как модель случайного процесса, представляющего собой развертку изображения
В частности, при n = kT получаем ковариа-
ции между витками
V ( kT ) =
q!
(1 - 5 2 )(1 - Г 2 )(1 - Ur )( Г - U )
X
x ( (1 - u 2) rk + 1 - (1 - r 2) uk + 1 ) . (4)
вдоль спирали:
xn
= s x n - 1 + r x n - T - s r x n - T - 1 + q ^ n , (2)
где n = kT +l . Параметр s влияет на коррелиро-
ванность вдоль строк, то есть на гладкость процесса. Параметр r влияет на коррелированность отсчетов на расстоянии периода. Очевидно, при значениях r , близких к единице, соседние строки изображения (витки спирали) будут сильно кор-
релированы, поэтому эту модель можно исполь-
зовать для описания и имитации квазипериоди-ческих сигналов. В [5] эта модель применена для
представления вокализованных звуков речи.
Ковариационная функция V(n) = Cov(xk,xk+n) модели (2) имеет вид
V ( n ) = q q
( 1
v (1 — r 2) T
T - 1
zk k^(1 - szk)(zk
- s )
n zk
+■
u
+-----z
(1 - s2)(1 - ru)(u - r)
где Z k = T T r exp( i 2 kn / T ) и u = sT .
Из (4) при k = 0 находим дисперсию процесса:
2 = q 2(1 + ru )
° (1 - 5 2)(1 - Г 2)(1 - ru ) . (5)
Из этих выражений следует, что ковариационная функция модели (2) является затухающепериодической (на рис. 2 показан график коэффициента корреляции). Значения этой функции постепенно убывают с увеличением номера периода, то есть с увеличением расстояния значения процесса становятся менее коррелированными, но на расстояниях, кратных периоду, корреляция большая.
На рис. 3 показаны примеры графиков процессов в виде разверток по спирали изображений на цилиндре, полученных с помощью модели (1). Квазипериоды на рисунке разделены вертикальными линиями. Квазипериоды на рис. 3б более коррелированы, чем на рис. 3а, в силу большего значения параметра r.
Для представления системы временных рядов можно использовать витки цилиндрического изображения [5-7]. Например, для одного
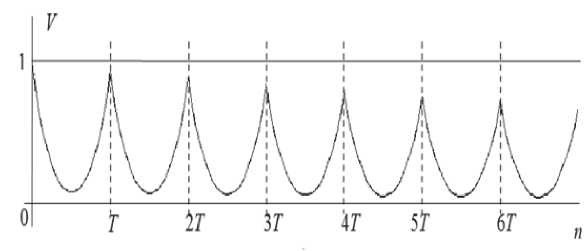
Рис. 2. График корреляционной функции
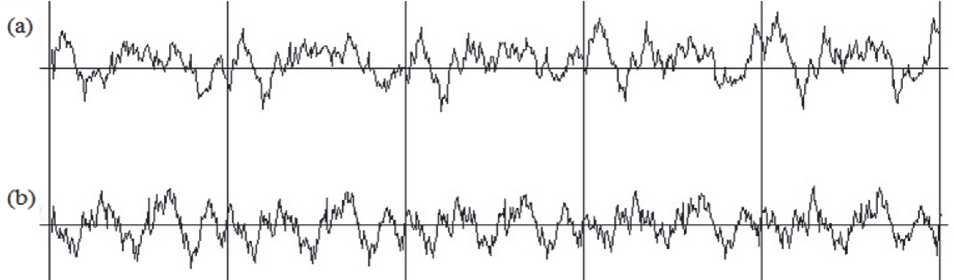
Рис. 3. Графики процессов:
a) с параметрами s = 0,9, r = 0,85; b) с параметрами s = 0,9, r =0,95
временного ряда взять витки, начиная с 1, а для второго – начиная с 21. Однако подобное представление годится только для небольших отрезков временных рядов, так как в этом случае второй ряд будет просто повторять первый ряд с временным сдвигом на 20 периодов. Поэтому рассмотрим модель, в которой каждый временной ряд системы представлен изображением на своем цилиндре, а эти отдельные цилиндры вложены друг в друга и образуют систему цилиндров – «многослойный цилиндр». На рис. 1с показаны два таких слоя.
Пусть задана система из m однородных случайных процессов X ={ xn,m, m= 1,2,…, M }, каждый из которых задан моделью (2), с ковариационной матрицей между процессами
C — {Cij } — {cov( xn,i, xn, j )} — {M [xn,ixn, j ], i — 1,2,..., M, j — 1,2,..., M}. (6)
Образуем сначала систему Y ={ yn,m, m= 1,2,…, M } из m независимых «стандартных» процессов с нулевым средним и единичной дисперсией с помощью модели вида (1), взяв в ней q 2 = q 2 = 1/ ст 2 , где s2 определено в (5):
y n , m — 5 У n - 1, m + r У n - T , m -
_ 5 ry n _ t - I, m + q | У n , m . (7)
Заданную систему X={xn,m, m=1,2,…,M} образуем в виде линейной комбинации стандартных процессов: Y = AX, то есть xn,m — S amj yn, j , m — 1,2,..., M . (8) j
Матрица А должна удовлетворять уравнению AAT = C и может быть взята нижней треугольной [8].
В частности, если Cij =s 2p|j-i| , то есть процессы xn,m имеют одинаковую дисперсию s2 и коэффициент корреляции p|j-i| между процессами xn,i и xn,j , то они могут быть получены из стандартных в виде авторегрессии первого порядка:
x n ,1 = CT У п ,1 ,
-
- ГТ"^ (9)
-
x n, m p x n,m - 1 + v1 p Уп,m ■
Отметим, что, переходя в формулах (6-9) от обозначений xn,m из модели (2) к обозначениям xk,l,m из модели (1), получаем систему изображений, определенных на системе вложенных друг в друга цилиндров.
На рис. 4-6 показаны примеры имитации систем из трех процессов каждая с различными параметрами модели в уравнениях (7) и (9). У процессов на рис. 4 параметр p = 0, поэтому эти процессы не коррелированы. На рис. 5 p = 0,5, поэтому наблюдается слабая корреляция между процессами. Процессы на рис. 5 более коррели- рованы, чем на рис. 4, так как параметр p имеет большее значение 0,9.
Таким образом, выбором параметров описанной модели можно представить системы квазипериодических процессов с требуемыми корреляциями внутри и между периодами, а также между процессами системы.
В [8] представлены модели изображений на круге. Для этого было использовано то же авторегрессионное уравнение (1), но в полярных координатах, то есть значение xk,l относилось к пикселю с координатами ( k A r , l Аф ) на радиально-круговой сетке с шагом ∆ r по радиусу и шагом Aj = 2 п / T по углу (рис. 7a), которую можно заменить и на спиралевидную (рис. 7b). На рис. 8 показан пример имитации трех изображений с различными значениями параметров: с параметрами r = 0,9, s = 0,8 (рис. 8а) и r = 0,8, s = 0,9 (рис. 8b). Первое из этих изображений больше коррелировано по радиусу, а второе – по окружности, что определяется соотношением между параметрами модели.
По аналогии с изображениями на системе цилиндров, модель (8) можно рассматривать как модель изображений на системе кругов. На рис. 7с изображены два круга. Это, например, дает возможность описания изображений сечений трехмерного стержня. На рис. 9 показан пример имитации изображений на системе из 9 кругов с параметрами s = 0,95, r = 0,8, p = 0,8. Круги, то есть процессы системы, на этом рисунке расположены в следующем порядке: в верхнем ряду – 1,2,3; во втором – 4,5,6; в третьем – 7,8,9. Изображения сильнее коррелированы по окружностям, так как s > r. Корреляция между изображениями экспоненциально убывает с увеличением расстояния меду ними.
СИНТЕЗ МОДЕЛИ
Пусть имеется система временных рядов Z = { zn,m, m= 1,2,…, M }. Предположим, что эта система (хотя бы приближенно) может быть представлена моделью (7, 8), параметры которой неизвестны. Требуется идентифицировать эту модель, то есть подобрать ее параметры так, чтобы эта модель наилучшим образом соответствовала системе Z . Для определенности будем понимать «наилучшим образом» в смысле минимума среднего квадрата ошибки предсказания рядов системы на один шаг вперед. В этом случае функционал качества, который следует минимизировать, имеет вид:
2-,
J ( а ) M [( xc n , m z n , m ) ] , (10)
где - X n, m — прогноз значения xn m по предшествующим значениям { xi,m , i ≤ n }.
В работе [9] эта задача рассмотрена в частном случае, когда имеется только один вре- менной ряд {zn}, то есть когда M = 1, а ряд {xn} представлен моделью (2), и требуется определить оптимальные значения параметров (s, r) в смысле минимума критерия (10). Возможным подходом к решению данной частной задачи является нахождение этих параметров по смыслу модели (2) в виде оценок коэффициентов корреляции ряда zn между соседними элементами витка и между соседними витками спирали. Данный подход является по сути идентификационным подходом к адаптации, когда неизвестные параметры заменяются их оценками.
Однако недостатком такого построения является дополнительное оценивание межвитковых и внутривитковых коэффициентов корреляции, что ведет к временной задержке. Кроме того, использование оценок этих коэффициентов в качестве параметров модели может не гарантировать наилучшего результата в смысле точности интерполяции или экстраполяции процесса. Поэтому применим другой подход к идентификации модели - безыдентификационный по параметрам. При этом подходе параметры модели выбираются так, чтобы наилучшим образом
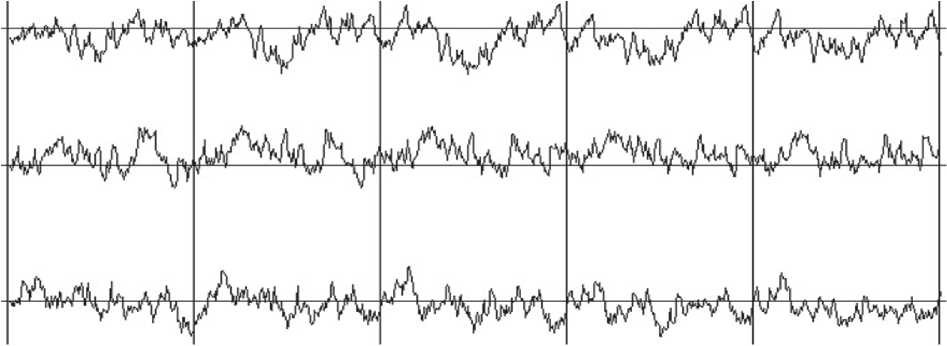
Рис. 4. Три процесса с параметрами s = 0,9, r = 0,9, p = 0
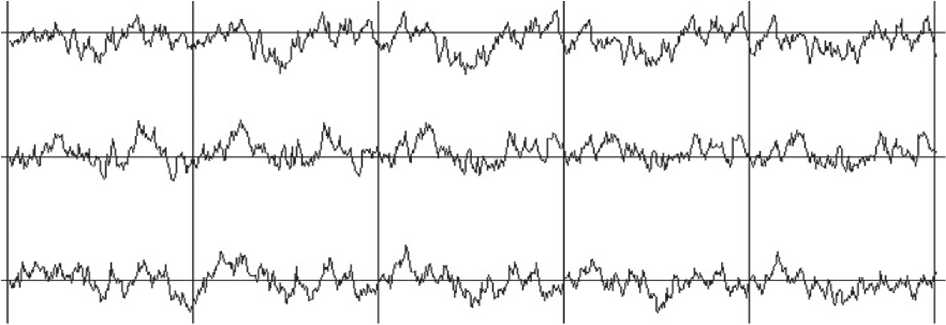
Рис. 5. Три процесса с параметрами s = 0,9, r = 0,9, p = 0,5
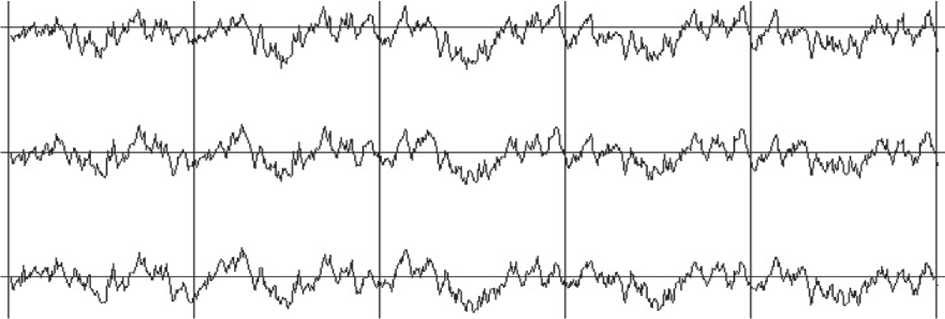
Рис. 6. Три процесса с параметрами s = 0,9, r = 0,9, p = 0,9
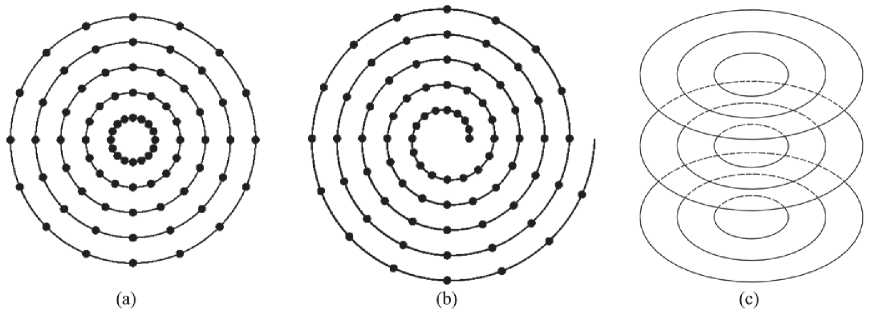
Рис. 7. Круговые сетки:
(а) на круге; (b) спираль на круге; (c) на системе кругов

Рис. 8. Изображения на круге с параметрами: (a) s = 0,9, r = 0,95; (b) s = 0,98, r = 0,9; (c) s = r = 0,9
обеспечивалось требуемое качество модели, в рассматриваемом случае – оптимальное предсказание процесса.
Пусть задача формулируется в виде минимизации функции J ( а ) = J ( а , Z ) для конкретной реализации Z по параметрам α . Применим для решения этой задачи псевдоградиентную процедуру [9, 13]:
а n =а n — 1 — Ц n V Q ( а n — 1 ) , (11) где а n - следующее за а n — 1 приближение к точке минимума функции J ( а ) ; m n - положительная числовая последовательность, определяющая длину шагов; V Q ( a n - 1 ) = V J ( а n — 1, Zn ) - усечение градиента критерия J ( а ) на небольшую область Zn наблюдений Z . При решении нашей задачи в качестве J ( а ) = J ( 5 , г ) берется (10). Тогда Q ( a n — 1 ) = J ( а n — 1, Zn ) - ошибка прогноза одного наблюдения, то есть
Q(аn ) = (5 xn—1 + Г xn—T - 5 r xn—T—1 — zn )2 .(12)
Градиент функции (12), состоящий из ее частных производных по s и r , легко вычисляется, поэтому реализация процедуры (11) не вызывает затруднений. Модель (2) содержит еще параметр q , связанный с дисперсией процесса соотношением (5), поэтому для оценивания этого параметра можно использовать выборочную дисперсию процесса.
Для точной оценки параметров следует выбирать последовательность µ n убывающей. Однако, если свойства временного ряда изменяются со временем, то и оптимальные значения параметров модели становятся переменными. Поэтому для их отслеживания следует эту последовательность ограничивать снизу, например, взять постоянной. Конкретные значения m n зависят от индивидуальных свойств поступающих данных и подбираются опытным путем.
Рассмотрим теперь систему временных рядов. В этом случае требуется найти значения параметров модели (7, 8), оптимальные в смысле минимума критерия (10). Эта задача может быть решена аналогично случаю единственного ряда с помощью псевдоградиентной процедуры, только с большим количеством параметров. Параметров может быть существенно меньше в частных случаях ковариационной матрицы С из (6). Например, для случая Cij = σ 2p|j-i| д обавляется только один параметр p , то есть а = ( 5 , r , p ) , и дополнительно нужно учесть коэффициент корреляции p между процессами, например, в виде:
Q ( 5 , Г , p ) = ( 5 x n — 1, m + Г x n — T , m — 5 Г x n — t — 1, m — z n , m )2 +
+ ( zn , m + 1 - Pzn , m )2 . (13)

Рис. 9. Система процессов в виде системы круговых изображений
Вместо этого можно просто оценить этот коэффициент по наблюдаемым рядам z n,m .
Отметим, что в рассмотренных моделях содержится параметр – длина квазипериода T . Однако для процессов рассматриваемого класса T легко определяется, например, по пику коэффициента корреляции [14].
РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТОВ
В экспериментах определялось СКО ошибки прогноза на один шаг. Проведенные эксперименты на реальных и имитированных процессах позволили сделать следующие выводы.
Если временные ряды описываются моделью (7, 9) точно, то идентификации по оценкам корреляции и псевдоградиентная давали практически одинаковые результаты. Псевдо-градиентная идентификация была точнее на несколько процентов при зашумлении наблюдений некоррелированными нормальными помехами с отношением сигнал/шум порядка 0dB. При очень сильных шумах оба метода давали близкие результаты. Псевдоградиентный метод существенно выигрывал (на десятки процентов) при даже незначительных отклонениях временных рядов от модели (7, 9), когда, например, в этой модели коэффициент при yn-T-1 изменен на 1-2% при неизменных значениях других параметров.
ЗАКЛЮЧЕНИЕ
В работе предложено моделировать систему квазипериодических процессов в виде отсчетов по спиралям на системе цилиндрических изображений. Каждый из процессов системы представлен своим цилиндром или кругом. Корреляции между процессами формируются линейным преобразованием системы авторегрессионных стандартных независимых между собой процессов с нулевым средним и единичной дисперсией. Варьируя небольшое количество параметров модели, можно представить широкий класс систем квазипериодических процессов. Для идентификации модели, то есть выбора ее параметров для наилучшего представления наблюдаемой системы временных рядов, предложено использовать псевдоградиентную процедуру подбора параметров этой модели по заданному критерию, например, по оптимизации прогноза процессов на один шаг вперед. Статистические испытания этой процедуры показали высокую точность оценки параметров модели. Эта процедура требует небольших вычислительных затрат и позволяет производить идентификацию модели однородных и неоднородных систем процессов в реальном времени.
Список литературы Модели систем квазипериодических процессов на основе цилиндрических и круговых изображений
- Бокс Дж., Дженкинс Г. Анализ временных рядов. Прогноз и управление. М. : Мир, 1974. 242 с.
- Андерсон Т. Статистический анализ временных рядов. М.: Мир, 1976. 756 с.
- Хеннан Э. Многомерные временные ряды. М.: Мир, 1974. 576 с.
- Пугачёв В. С., Синицын И.Н. Теория стохастических систем. М.: Логос, 2000. 1000 с.
- Кляцкин В.И. Стохастические уравнения. В двух томах. М.: Физматлит, 2008. 320 и 344 с.
- Клячкин В.Н., Кувайскова Ю.Е., Алёшина А.А. Моделирование вибраций гидроагрегата на основе адаптивных динамических регрессий // Автоматизация. Современные технологии. 2014. № 1. С. 30-34.
- Крашенинников В.Р., Кувайскова Ю.Е. Прогнозирование динамики объекта с использованием авторегрессионных моделей на цилиндре // Радиотехника. 2016. №9. С. 36-39.
- Krasheninnikov V.R., Kalinov D.V., Pankratov Yu.G. Spiral Autoregressive Model of a Ouasiperiodic Signal // Pattern Recognition and Image Analysis. Vol. 11. No. 1. 2001. - P. 211-213.
- Krasheninnikov V.R., Vasil'ev K.K. Multidimensional Image models and processing // Intelligent Systems Reference Library. 2017. Vol. 135. P. 11-64.
- Хабиби А. Двумерная байесовская оценка изображений // ТИИЭР. 1972. Т. 60. №7. С. 153-159.
- Гантмахер Ф.Р. Теория матриц. М.: Наука, 1966. 576 с.
- Крашенинников В.Р. Идентификация цилиндрической модели квазипериодического процесса // Известия Самарского научного центра РАН. 2018. Т. 4(3). С. 483-486.
- Поляк Б.Т., Цыпкин Я.З. Псевдоградиентные алгоритмы адаптации и обучения // Автоматика и телемеханика. 1973. № 3. С. 45-68.
- Серебренников М.Г., Первозванский А.А. Выявление скрытых периодичностей. М.: Наука, 1965. 244 с.


