Модели событийных недетерминированных автоматов для формального представления основных свойств систем управления параллельными процессами и ресурсами

Формальное аналитическое описание основных свойств систем управления необходимо, с одной стороны, для аналитического представления алгоритмов управления параллельными процессами и ресурсами, а с другой – для верификации таких алгоритмов. При этом основные свойства систем управления (СУ) должны быть такими, чтобы обеспечивалось выполнение основных характеристик таких систем, к числу которых относятся – надежность и эффективность систем. В связи с этим для реализации таких СУ и их верификации необходимо использовать математический аппарат, который, с одной стороны, обеспечивал бы формальное аналитическое представление сложных алгоритмов управления, а с другой – отличался бы простотой и компактностью.

В качестве такого математического аппарата в данной статье предлагается использовать модели событийных недетерминированных автоматов (СНДА), которые обладают следующими достоинствами [12]: во-первых, модели СНДА отличаются значительной простотой и компактностью, так как описание свойств СУ выполняется не в терминах состояний детерминированных автоматов (ДА), а в терминах частных событий, реализуемых в системах управления, учитывая при этом, что число таких частных событий m СНДА будет значительно меньше числа состояний М эквивалентного ему ДА, так как         . Во-вто рых, использование моделей СНДА предоставляет широкие возможности для описания сложных алгоритмов управления параллельными процессами и ресурсами, так как основой таких моделей является практически сеть, вершины которой отождествляются с некоторыми событиями, а дуги – соотношениями между этими событиями [1-4].

Основные свойства СУ параллельными процессами и ресурсами и их формальное описание, когда события в явном виде зависят от времени

Для увеличения производительности решения сложных вычислительных задач или задач промышленной автоматики такие задачи обычно разбиваются на параллельные ветви. В связи с этим возникает необходимость в реализации синхронизации взаимодействия таких параллельных ветвей (процессов) при обращении к общим критическим ресурсам или при обмене сообщениями. Для этой цели используют различные механизмы синхронизации процессов, к числу которых относятся критические интервалы, мониторы, кольцевые буферы, рандеву и др.

Для обеспечения надежности и эффективности таких СУ параллельными процессами и ресурсами к используемым механизмам синхронизации предъяв- ляют необходимые требования, которые являются основой определения и реализации основных свойств таких систем [5-6]. В качестве примера рассмотрим, какими свойствами должны обладать события, реа- лизующие управление параллельными процессами, при использовании механизмов критических интервалов и мониторов. К числу таких основных свойств относятся справедливость, достижимость, взаимоисключение и приоритетность событий, определяющих вход процессов в свой критический интервал или в монитор и нахождение в них.

События, определяющие вход i -го процесса в

( i \

5K J или в монитор

(5 м ) ’ можно представить таким образом [7]:

^K

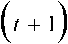
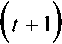
5ВП,К ^ВЗ,К5Пр,К V 5К5/7К ’ W

5вп,м *^вз,м^пр,м ^v S_MS_MnS_nM • (2)

В уравнениях (1)-(2) первая составляющая, представленная конъюнкцией событий, определяет вход i-го процесса в свой критический интервал (1) или монитор (2). Эти события и определяют отмеченные выше свойства, в том числе и свойства справедливости и достижимости, которые опре-z деляются событиями типа 5Bn" Эти события для используемых механизмов синхронизации должны быть представлены в следующем виде:

^ВП,к(, + О ( ^3 v ^ВП,к)^К ’      (3)

Sm Smh’ ^)

^вп^у /       ^вп,м z z где S вп,к и 5 вп,м – события, свидетельствующие о восприятии заявки i-го процесса (событие z iS з ) к общему критическому ресурсу и ее сохранение только в том случае, когда данный процесс не находится в своем критическом интервале (3) или в мониторе (4) соответственно. Это означает, что ни один процесс не будет бесконечно долго ждать входа в свой критический интервал или монитор.

Событие S мп свидетельствует об отсутствии повторного входа в монитор i -го процесса, который ранее вышел из монитора не обслуженным. В данном случае это обеспечивает свойство справедливости для таких процессов.

Вторая составляющая уравнений (1)-(2), представленная конъюнкцией событий, определяет время нахождения i-го процесса в своем критическом интервале (1) или монитора (2). В данном z случае событие S пк свидетельствует об окончании одноразовой операции i-го процесса с общим критическим ресурсом. i

Событие S им свидетельствует об окончании одноразовой операции i-го процесса с общим критическим ресурсом, если данный i-ый процесс не вышел из монитора не обслуженным ( Smz?) = 1 ■ Свойство достижимости событий

SK и Sm обеспечивается наличием события z типа iS вп ’ которое является обязательным непосредственно предшествующим для таких событий. Необходимо отметить, что проверить наличие достижимости всех частных событий, реализуемых в СУ, можно путем построения прямой таблицы переходов (ПТП) для этих событий по определенному правилу. Это правило заключается в том, что оче- редная строка ПТП должна начинаться с представлением такого события, которое уже было отмечено в одной из предшествующих строк ПТП [1-2].

Свойство взаимоисключения событий типа

5_K ^и 5_m

обеспечивается входом в одно и то же время в критический интервал или монитор только одного i-го события из n-процессов. Это свойство формализуется следующими комбинационными событиями:

i ,

5вз,к(/ + 1)= ASk ;

(Va)[a*/]

sUmO + D-A^,,.(6)

(Va)[a*z]

Свойство наличие приоритетности процессов обеспечивает однозначность входа i-го процесса в свой критический интервал или монитор. Наличие приоритетности событий особенно необходимо в начальный период при обращении процессов к общему ресурсу, когда могут быть i i истинными все события типа 5вз и 5Bn .

В качестве примера рассмотрим приоритетность i-го процесса для циклической дисципли-i ны обслуживания S np [6]. Это событие можно представить следующим выражением:

Snp(^? + D = Snp(°) v 5вп5т ’      (7)

где S пр^^ – представляет собой сокращенное обозначение комбинационного события, определяющего начальный приоритет обслуживания i -го процесса:

Snp(O) ^О^и^ВП Л 5вП; (Va )[«]

SoU + о - хо v So.xn ’

где ^хп – сигнал СУ; x ₀ – сигнал приведения 1

СУ в начальное состояние; St – сокращенное обозначение комбинационного события, определяющего приоритет i -го процесса при наличии воспринятой заявки в повторных циклах циклической дисциплины обслуживания;

ST = V pk К SbJ ’      (9)

z=l ^a)^a>i)

где S p]^ – сокращенное обозначение события, определяющего выход i -го процесса из критического интервала или монитора после окончания процедуры обращения к разделяемым данным.

Основные свойства систем управления параллельными процессами и ресурсами и их формальное описание, когда события не зависят в явном виде от времени

В работе [8] рассматривается язык временной темпоральной логики, когда порядок событий в системе описывается без привлечения времени в явном виде. В данном разделе рассматриваются вопросы описания основных свойств таких систем на основе использования моделей СНДА.

В связи с этим будут показаны широкие возможности языка СНДА для описания сложных систем управления, когда события, представленные в таких системах, не зависят в явном виде от времени. К числу основных свойств таких событий согласно [8] относятся следующие: достижимости, достижимости в будущем «рано или поздно», инвариантности, условного ожидания и разблокировки.

Свойство достижимости «в следующий момент» ( Х ), означающее что любое событие S j будет достижимо тогда, когда имеет место событие, непосредственно предшествующее ему, то есть такое свойство уже было рассмотрено при описании событий в (1)-(2).

Свойство «рано или поздно», или «когда-то в будущем» (F) . В данном случае таким свойством будет обладать некоторое событие S j , которое будет истинным только в том случае, когда станет истинным некоторое событие S p (определяющее условие зарождения события S j ), время наступления которого точно не определено.

Учитывая это обстоятельство, вводят вспомогательное событие S ,- ’ которое для события S' j будет играть роль непосредственно предшествующего события. Тогда описания таких событий будут иметь вид

Sy(? + 1) SrSpv SjSj,K - srV + 0 = Ur,3 v SrJSj , где S г,з – событие, определяющее зарождение события Sr ’ S'y,K – событие, определяющее условие сохранения события S' j .

Свойством инвариантности, или «всегда, повсюду», ( G ) будет обладать некоторое событие S j , которое будет истинным всегда (повсюду) для всех n- непосредственно предшествующих событий (sz) для события ^ j , то есть событие S' j можно представить как

J                 n                  -----

S/? + D = V (S_Z.)S₇;₃^v SjSj,_K , (11)

где Sj з – событие, определяющее условие зарождения события 1S j .

Свойство условного ожидания, или «до тех пор, пока», ( U ) – в данном случае таким свойством будет обладать некоторое событие S j , которое не будет истинным долго – до тех пор, пока не будет истинным некоторое событие S p . При этом каждое из n непосредственно предшеству-(z \

Sr) (для события S j ) после зарождения события S j станет равным нулю

I Sr = 0 h то есть каждое событие типа S у тоже будет обладать отмеченным свойством «до тех пор, пока».

Учитывая это обстоятельство, события S j и z

S у будут иметь вид

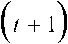
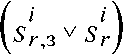
П /    . X

SjU +1) = v ( s^l_r)S_p z'=l

v sj4k

Свойство разблокировки, «высвободить» (R). В данном случае свойство «высвободить» отно- сится к некоторому событию Sj ’ которое после зарождения будет существовать (то есть остается истинным) до тех пор, пока не зародится некоторое событие S p' которое, в свою очередь, может ни- когда и не зародиться, если событие, реализующее его зарождение, S p — о . Учитывая это, описание событий

и S_r будут иметь вид

Si

Sj(t + ^ = UiSj3v Sj)sr

SrV + ^) = SjSp v srsr,K , где ^ i – событие, являющееся непосредственно предшествующим событию S' j .

В заключение отметим, что полученные представления событий, реализуемых в вычислительных многопроцессорных системах или в системах управления объектами промышленной автоматики, в виде системы канонических уравнений (модель СНДА), естественно по шагам отражают алгоритмы работы преобразования информации, что позволяет осуществить переход к различным вариантам их реализации: аппаратно , программно или в виде их комбинаций и выполнить их верификацию путем моделирования на модели [8-10]. Работа выполнена в рамках федеральной целевой программы «Научные и научно-педагогические кадры инновационной России» на 2009-2013 г.г. (соглашение № 14.B37.21.0597).