Модели строения областей когерентного рассеяния антрацита, стеклоуглерода и шунгита

Углеродные материалы находят широкое применение в современных высоких технологиях, в различных отраслях машиностроения и электротехники, атомной и космической промышленности [4]. В настоящеее время принято считать, что аморфный углерод в различных природных и синтетических формах по своей структуре приближается к графиту в разной степени [7]. Поэтому для более полной характеристики строения углеродных материалов необходимо проводить рентген-дифракционные исследования их структуры [4].

В работе исследовались образцы природных углеродных материалов (антрацита и шунгита) и синтетического происхождения (стеклоуглерода). Из антрацита и шунгита были получены порошки, из которых были изготовлены плоскопараллельные пластинки. Образец стеклоуглерода представлял собой плоскопараллельную пластинку стеклографита марки СУ-2000. Изотропию объектов исследования доказывало совпадение исправленных на поглощение кривых рассеяния, полученных в геометриях Лауэ и Брэгга.

Интенсивность рассеяния регистрировалась на дифрактометре ДРОН-6 в MoK α излучении монохроматизированном кристаллом пиролитического графита, установленным в первичных лучах. В экспериментальные кривые, усредненные по 10 съемкам, вводились поправки на рассеяние воздухом, поляризацию и поглощение.

^M N ^M N ^Smax f 2 (S)

D(r) = ∑ P i (r) = ∑             exp( - α 2 S 2 )exp( - σ²S 2 )sin(Sr i )sin(Sr)dS.

r i r i g 2 (S)                          ⁱ

Коэффициент перевода в электронные единицы на атом рассчитывался по методу Уоррена [1], [8].

Из нормированных кривых распределения интенсивности I(S) рассчитывалась S-взвешенная интерференционная функция: H(S) = Si(S)exp( -α 2 S 2 )g -2 (S). Здесь S = 4 π sin θ / λ – длина дифракционного вектора, θ – угол скольжения рентгеновских лучей, λ – длина волны излучения, g ^-2 (S) – фактор обострения, повышающий контрастность интерференционной функции рассеяния i(S) = I(S) - f C² (S) при больших значениях S; exp(- α 2 S 2 ) – фактор затухания, вводимый для уменьшения влияния ошибок эксперимента при больших значениях S.

Функция H(S) является подынтегральной для расчета кривой распределения парных функций

D(r) : D(r) = 2 2r eZC +^Sm ∫ ^axH(S) ⋅ sin(SR) ⋅ dS.

Коэффициент затухания α был выбран равным 0,1, а фактор обострения рассчитывался как эффективная функция рассеяния на электрон [1], [8].

Верхний предел интегрирования S max составлял 16,85 Å ^-1 . При работе методом Финбака [1], [8] рассчитанная из H(s) кривая D(r) представляется в виде суммы парных функций P ij (r) [1], [8]. Для случая однокомпонентного материала выражение для D(r) имеет вид:

Координационные числа N i из системы уравнений (1) находились методом наименьших квадратов с использованием метода сингулярного разложения (SVD) матрицы. Радиусы координационных сфер в первом приближении задавались как средневесовые значения r i^кр , рассчитанные для графита по методике, изложенной в [3]. Затем радиусы координационных сфер r i и их размытия о , подбирались методом проб и ошибок [8].

Распределения интенсивности рассеяния I(S) (рис. 1а) и соответствующие им кривые распределения S-взвешенной интерференционной функции H(S) (рис. 1б) различаются для всех трех исследованных объектов в первую очередь интенсивностью максимумов. Кроме того, первый максимум, характеризующий рассеяние пакетом графеновых сеток и имеющий индексы интерференции (002), на кривой рассеяния шунгитом заметно смещен в сторону бόльших углов рассеяния (рис. 1а).

Из полученных кривых H(s) были рассчитаны кривые распределения парных функций D(r) (рис. 2).

В таблице приведены результаты расчета характеристик ближнего порядка для исследуемых образцов. Степень несоответствия экспериментальной кривой (D эксп (r)) и кривой D подб (r), рассчитанной по найденным значениям координационных чисел N i и подобранным значениям радиусов r i и размытий о , координационных сфер (см. таблицу), составила для антрацита 4,6 %, для стеклоуглерода 2,7 % и для шунгита 4,9 %.

Здесь r i^кр и N i^кр – средневесовые значения радиусов координационных сфер и суммарные координационные числа для гексагонального графита. Первые три радиуса координационных сфер характеризуют углеродное кольцо графеновой сетки. Значение кратчайшего расстояния между атомами углерода выше, чем в графите: на 14 % для шунгита и антрацита и на 20 % для стеклоуглерода. Радиус первой координационной сферы для антрацита, а также координационное число согласуются с данными, приведенными в работе [5]. Уменьшение первого координационного числа по сравнению с графитом может быть обусловлено конечным размером графеновых сеток. Наиболее высокие значения радиуса второй координационной сферы и второго координационного числа наблюдаются у стеклоуглерода.

Следующее межатомное расстояние в кольце (третья координационная сфера) завышено по сравнению с таковым для графита на 21, 14 и 7 % у антрацита, стеклоуглерода и шунгита соответственно. Координационное число на этой сфере у антрацита и стеклоуглерода на 10 % выше, чем у графита и шунгита. Заниженные значения координационных чисел на первых двух сферах для шунгита свидетельствуют о том, что графеновые сетки шунгита по строению в среднем близки к сеткам в графите, но в них есть вакансии.

Сетки антрацита и стеклоуглерода, по-видимому, искажены.

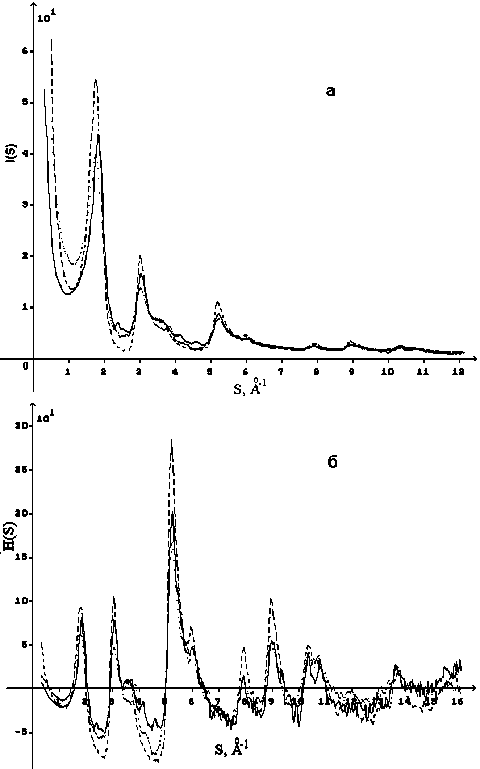
Рис. 1. Кривые распределения интенсивности рассеяния (а) и H(S) (б):

•••• антрацит, — стеклоуглерод, — шунгит

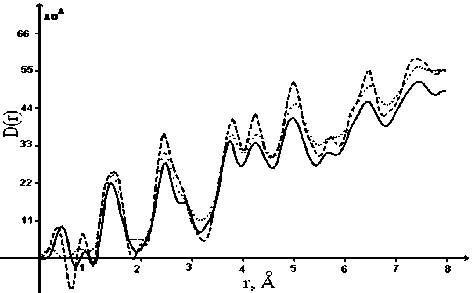
Рис. 2. Кривые распределения парных функций D(r): ... антрацит, — стеклоуглерод, — шунгит

Радиус четвертой координационной сферы соответствует кратчайшему межсеточному расстоянию, оно у стеклоуглерода и антрацита занижено. Координационные числа на этой сфере у антрацита и шунгита завышены по сравнению с графитом и стеклоуглеродом. Радиус пятой координационной сферы для графита (3,68 Å) был рассчитан как средневесовое значение двух межатомных расстояний: 3,635 и 3,752 Å (координационные числа 9 и 6 соответственно), из которых первое соответствует межсеточным расстояниям, а второе – расстояниям между атомами в сетке. Экспериментальное значение радиуса 3,73 Å ближе по величине к внутрисеточному расстоянию, а координационное число на данной сфере у всех исследованных образцов занижено по сравнению со значением суммарного координационного числа для графита (15), причем у шунгита почти вдвое. Такое изменение координационных чисел на четвертой и пятой сферах, вероятнее всего, связано с разориентацией ближайших соседних сеток, то есть разворотом их относительно друг друга вокруг нормали к сеткам. Данный результат согласуется с турбостратной моделью Уоррена [5].

На остальных координационных сферах (6– 15) отличие значений радиусов для стеклоуглерода и шунгита от таковых для графита лежит в пределах ± 0,03 Å, за исключением 10-й сферы для стеклоуглерода, значение радиуса которой на 0,04 Å выше, чем для графита. Радиусы сфер 6–15 для антрацита отличаются от радиусов сфер графита в основном в сторону увеличения, и максимальное различие наблюдается для 10-й сферы (+0,09 Å). Координационные числа на 6– 15-й сферах у антрацита и стеклоуглерода коррелируют между собой и отличаются от соответствующих значений для графита то в меньшую, то в большую сторону. Координационные числа для шунгита на всех указанных сферах, кроме 8-й, 9-й и 14-й, ниже, чем для графита.

Таким образом, области ближнего упорядочения в исследуемых образцах по своей организации отличаются от соответствующих областей гексагонального графита и друг от друга распределением атомов по координационным сферам при сохранении радиусов.

Сущность турбостратной модели Уоррена [5] в том, что основная часть углей представлена углеродным веществом, находящимся как в виде одиночных сеток, так и в виде пакетов из нескольких сеток. Пакеты могут состоять из полностью параллельных сеток или из сеток, параллельных лишь своими нормалями, а в остальном произвольно ориентированных.

Цель дальнейших расчетов – поиск модели взаимного расположения атомов в области ближнего упорядочения исследуемых объектов путем построения конфигураций атомов, состоящих из углеродных сеток, расчет для них кривых H(s) и сравнение последних с экспериментом. Формировались кластеры из случайно развернутых слоев – как плоских, так и изогнутых. Основными варьируемыми параметрами для построения углеродных сеток были: число атомов в сетке, дисперсии случайных смещений атомов из положения равновесия, углы и дисперсии углов разворота сеток, радиусы изгиба сеток. Кроме того, нарушить структуру сетки можно было путем введения вакансий. Для каждого сформированного кластера проводился расчет интенсивности рассеяния I(s) и интерференционной функции рассеяния H(s) (расчетные формулы приведены в [2]), которые сравнивались с соответствующими экспериментальными кривыми.

Как указывалось в [6], при случайном смещении атомов из положения равновесия (аналогичного тепловому движению) происходит уменьшение интенсивности максимумов (рис. 1б) на кривой H(s) для модели. При этом появляется дополнительное фоновое рассеяние между максимумами, аналогичное ТДР. Увеличение числа сеток в пакете приводит к увеличению интенсивности первого и третьего максимумов на H(s). Изогнутость сеток влияет на ширину и форму максимумов. Было установлено, что кривая H(s), рассчитанная для модельного кластера, состоящего из четырех изогнутых слоев радиусами 40 Å и 60 Å, хорошо описывает экспериментальную кривую H(s) для антрацита (рис. 3).

Значения радиусов и размытий координационных сфер

	и координационные числа. Δ ri =						± 0,0	1, Δσ i = 0,0	2 Å
	Гр. гекс. A = 2,456Å		Антрацит			Стеклоуглерод			Шунгит
№ сф.	r iкр , Å	N iкр , ат.	r i , Å	σ i , Å	N i ± Δ N i , ат.	r i , Å	σ i , Å	N i ± Δ N i , ат.	r i , Å	σ i , Å	N i ± Δ N i , ат.
1	1,42	3	1,44	0,15	2,8 ±0,1	1,45	0,14	3,0 ±0,1	1,44	0,10	2,3 ± 0,1
2	2,45	6	2,46	0,16	6,2 ± 0,1	2,47	0,15	6,8 ± 0,2	2,45	0,18	5,7±0,2
3	2,83	3	2,9	0,12	3,3 ± 0,1	2,88	0,07	3,2 ± 0,1	2,85	0,14	3,0 ± 0,1
4	3,34	1	3,28	0,00	1,6±0,2	3,25	0,00	0,3 ±0,2	3,35	0,00	2,2 ± 0,2
5	3,68	15	3,73	0,22	11,1 ± 0,3	3,73	0,22	12,0 ± 0,5	3,73	0,10	7,9 ± 0,3
6	4,26	21	4,28	0,29	16,0 ± 1,0	4,28	0,24	17,2 ± 0,4	4,26	0,30	16,2 ± 0,3
7	5,01	30	5,01	0,35	27,0 ± 0,8	4,99	0,28	26,0 ± 0,6	4,97	0,28	20,3 ± 0,7
8	5,41	6	5,41	0,24	6,6±0,4	5,41	0,21	7,2±0,7	5,44	0,30	10,3 ±0,4
9	5,67	3	5,7	0,15	6,8 ± 0,2	5,68	0,12	5,0 ± 0,6	5,69	0,12	3,9 ± 0,5
10	6,07	30	6,16	0,4	31,8 ± 0,2	6,11	0,42	31,0 ± 1,0	6,07	0,32	20,4 ± 0,8
11	6,57	26	6,6	0,26	19,0 ± 2,0	6,55	0,24	20,0 ±2,0	6,54	0,28	25,8 ± 1,3
12	7,05	36	7,12	0,4	28,0 ± 1,0	7,06	0,41	29,0 ± 2,0	7,06	0,29	20,0 ± 2
13	7,31	24	7,26	0,35	17,0 ± 2,0	7,31	0,26	16,0 ± 1,0	7,31	0,30	14,0 ±2
14	7,55	12	7,55	0,2	15,0 ± 2,0	7,55	0,27	19,8 ± 2,0	7,55	0,30	14,0 ±2
15	7,86	39	7,92	0,23	35,0 ± 1,0	7,86	0,24	26,8 ± 2,0	7,86	0,38	36, ± 3

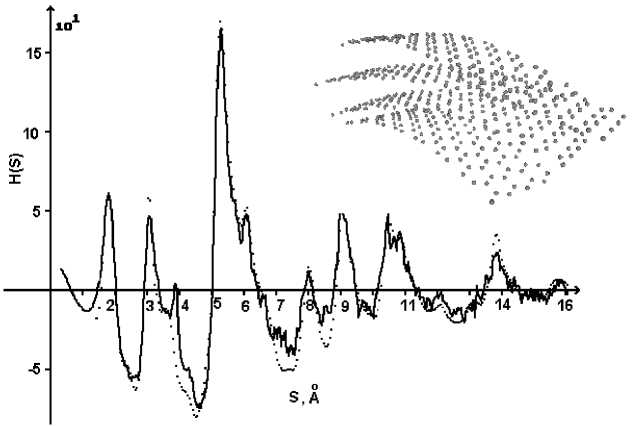
Рис. 3. Сравнение интерференционной функции распределения для модели и эксперимента для антрацита (в верхнем правом углу представлена модель, для которой рассчитана H(s))

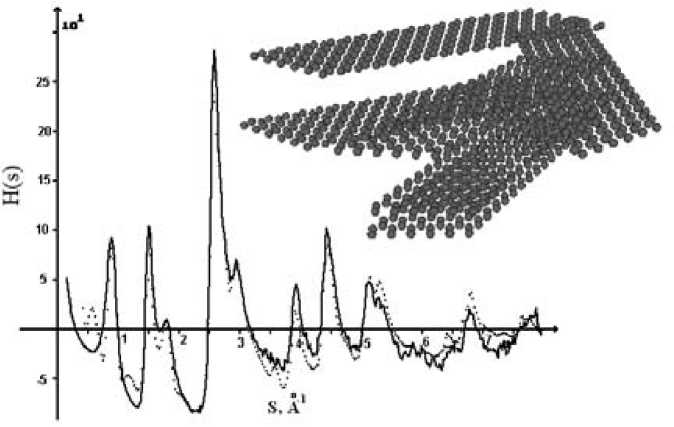
Рис. 4. Сравнение интерференционной функции распределения для модели и эксперимента для стеклоуглерода (в верхнем правом углу представлена модель, для которой рассчитана H(s))

Указанный модельный кластер (рис. 3) состоит из 512 атомов углерода. Межсеточное расстояние – 3,5 Å. Средний угол разворота вокруг нормали к графиновым сеткам второго и третьего слоя относительно первого составил 20º с дисперсией ±10º, а средний угол разворота четвертого углеродного слоя относительно первого был равен 5 ± 10º.

Смещение в плоскости графенового слоя второго и третьего слоя относительно первого составило 1,42 Å.

Наилучшего варианта описания структуры стеклоуглерода и шунгита удалось достичь путем построения пакетов из плоских сеток.

В случае стеклоуглерода пакет сеток состоял из 6 графеновых слоев и содержал 1296 атомов . Размер одного углеродного слоя – 50 × 13 Å, а размер кластера – 60 × 57 × 20 Å. Межсеточное расстояние для данного пакета изменялось следующим образом: расстояние между первым и вторым слоем составляло 3,43 Å; далее межсеточное расстояние постепенно возрастало до 3,54 Å, то есть пакет сеток получился как бы разреженным, дисперсии межслоевых расстояний были равны ±0,01 Å.

Все сетки в пакете были повернуты относительно первого слоя. Средний угол поворота 2– 6-го слоев варьировался в приделах дисперсий ±10º … ±30º. Кроме того, варьировался параметр, отвечающий за смещение углеродных слоев относительно друг друга. Смещение второго и четвертого слоя относительного первого в плоскости графеновых слоев составил 1,42 Å.

На рис. 4 представлен вид модельного кластера, полученного для стеклоуглерода, и интерференционные функции распределения для модели и эксперимента.

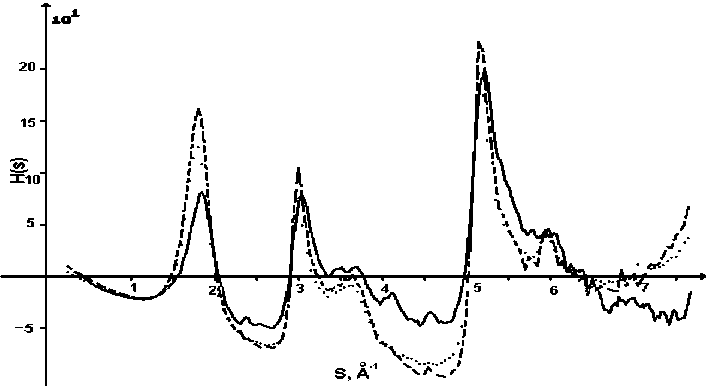
Рис. 5. Интерференционная функция рассеяния исследуемого образца (—), шунгита месторождения Шуньга (---) и месторождения Максово (….)

Рис. 6. Сравнение интерференционной функции распределения для модели и эксперимента для шунгита (в верхнем правом углу представлена модель, для которой рассчитана H(s))

В работе [6] были построены модели пространственного расположения атомов для углеродной составляющей образцов шунгита различных месторождений (Шуньга и Максово). Известно, что шунгиты различных месторождений имеют разную степень содержания углерода, она может колебаться от 1 до 99 %. Остальная часть шунгита представлена различными химическими примесями. Образец, исследованный в данной работе, был очищен от примесей электрохимическим способом. Рентгенограммы шунгитов различных месторождений и рассчитанные из них интерференционные функции отличаются друг от друга (рис. 5). Следовательно, и модели строения областей ближнего упорядочения будут различны.

В [6] было установлено, что для шунгита из месторождения Максово кластер состоял из шести углеродных сеток. Пять слоев кластера были плоскими с числом атомов 500 в каждом, а один – изогнутый с таким же числом атомов. Межсеточное расстояние задавалось d = 3,45 Å, а дисперсия угла случайных разворотов сеток – 10º. Также было задано смещение атомов из положения равновесия на 0,1 Å и введены вакансии (удалены 70 атомов).

Для шунгита месторождения Шуньга были предложены две модели: оба пакета состоят из шести графеновых слоев, три плоские сетки, состоящие из 500 атомов, три плоские сетки по 300 атомов в каждой. Межсеточное расстояние составило 3,45 Å, а дисперсия случайного разворота угла – 10º; другой кластер был сформирован из шести сеток, где три плоские сетки содержат по 500 атомов, две плоские сетки – по 300 атомов, одна изогнутая сетка состоит из 400 атомов.

Для исследованного в данной работе образца шунгита экспериментальные кривые интерференционной функции рассеяния наилучшим образом соответствуют таковым для пакетов из плоскопараллельных сеток со смещением атомов из положения равновесия на величину 0,1 Å. Прямоугольная область, куда помещается кластер, составляет (54 × 54 × 17) Å. Кластер состоит из шести слоев, пять из них плоские размером 45 × 50 Å, а шестой изогнутый слой имел размер 40 × 40 Å. Смещение атомов позволило достичь хорошего совпадения теоретической и экспериментальной кривых H(s) (рис. 6).

Межсеточное расстояние между первой и второй сетками составило 3,44 Å, а между вто- рой, третьей и последующими – 3,50 Å. Помимо этого, вторая и четвертая сетка были развернуты на 65 ± 10º относительно первого слоя. Разворот всех остальных сеток был случайным в пределах дисперсии 20º, и конечный угол разворота составил у третьего слоя 12,0º, у пятого и шестого – 7 и 4º соответственно. За счет смещения пятой сетки относительного первой на 1,48 Å удалось понизить максимум на кривой H(s) в области 3,7 Å-1.

Таким образом, анализ интерференционной функции рассеяния H(s) позволил построить модели, характеризующие расположение атомов в области ближнего упорядочения аморфных углеродных материалов.