Модели телетрафика на основе современной теории массового обслуживания

Статья посвящена исследованию систем массового обслуживания (СМО) G/G/1 с произвольными входными распределениями с коэффициентами вариаций интервала между поступлениями требований и времени обслуживания меньшими и большими единицы, то есть перекрывающими весь интервал (0, ∞). Для этого рассмотрены системы M-/M-/1 c запаздыванием во времени [1] и H2/H2/1, Н2/M/1, M/H2/1 с гиперэкспоненциальными входными распределениями [2-4] с целью получения решения для среднего времени ожидания требований в очереди. Для этого использован метод спектрального разложения решения интегрального уравнения Линдли . Для практического применения полученных результатов использован метод моментов .

В [1] показано, что коэффициент вариации случайной величины, распределенной по экспоненциальному закону с запаздыванием во времени, меньше единицы. Известно, что распределенная по гиперэкспоненциальному закону Н2 случайная величина имеет коэффициент вариации больше единицы. Учитывая, что распределение Н2 является трехпараметрическим, в статье приведен механизм аппроксимации произвольных законов распределений гиперэкспоненциальным на уровне двух и трех первых моментов .

Решение для системы M/M/1с запаздыванием: случай ся < 1, с < 1

Рассмотрим систему массового обслуживания (СМО), на вход которой поступают требования, случайные интервалы между которыми распределены по закону [1]:

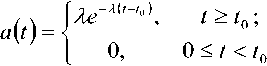
Аналогично распределено и время обслуживания:

6(0

'Ме"А*",й\

О,

0 <

Графическая иллюстрация функции плотности с запаздыванием во времени (1) приведена на рис. 1.

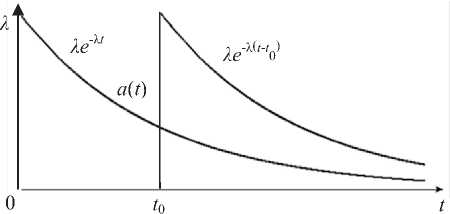
Рис. 1. График функции плотности c запаздыванием (1)

Функции плотности (1) и (2) сдвинуты вправо от нуля на величину экспоненциальными распределениями с параметрами , причем λ <  μ . Таким образом, мы имеем СМО с запаздыванием во времени [1]. В работе [1] приведено преобразование Лапласа функции плотности времени ожидания, полученное методом спектрального разложения решения интегрального уравнения Линдли:

W * (s) = 5 • ф ₊ (s) = ^ ^^^Х (s + ц -Л)

и полученное через него среднее время ожидания

W = ^-р-Х

Для определения неизвестных параметров формулы (3) получена система уравнений:

Я + tg Т^ (1 + At₀ ) ¹ = с _л; м"^х -+гд=т_м; О + ^о)"¹ =^Сц.

где числовые характеристики в правых частях системы: средние значения интервалов коэффициенты вариации           меньшие единицы при           будут входными пара метрами для определения неизвестных параметров.

В связи с этим мы имеем немарковскую модель массового обслуживания, где среднее время ожидания требования в очереди для системы M-/M-/1 будет меньше, чем в классической системе M/M/1 при одинаковом коэффициенте загрузки. Кроме того, использование функций плотности (1) и (2) позволяет аппроксимировать исходные входные распределения на уровне двух первых моментов, что обеспечивает лучшую точность, в отличие от классической системы M/M/1.

В качестве примера рассмотрим случай высокой нагрузки при параметрах:

и         . В этом случае получим загрузку

, а из (4) значения           и         ,

.

Тогда среднее время ожидания по формуле (3) для системы M-/M-/1:

• -_ 18/11/2 _ 18-11 _ 9 ,

~ 2-18/11 ” 4-22 ” 4

Система М/М/1 при той же нагрузке дает й=^1.9 то есть в четыре раза большую за держку.

Таким образом, рассмотренная СМО с запаздыванием позволяет рассчитать ее характеристики при коэффициентах вариации интервалов между поступлениями требований c₂ и времени обслуживания c_u меньших 1 при некоторых ограничениях на входные параметры системы, наложенных системой (4).

Решение для системы Н ₂ /Н ₂ /1: случай

C X — 1’ C n — 1

В работе [2] автором найдено преобразование Лапласа для функции плотности времени ожидания для системы Н2/Н2/1:

^ * (₅) = ^ (^ ⁺ /Л ) (^ ⁺ P^ )        (5)

^^(s + ^J^ + ^J где 5i и .S'2 – отрицательные вещественные части корней кубического уравнения

5³ -C^ -c,s-c₀ =0.       (6)

Коэффициенты этого уравнения:

c₀ = a_ob_v - а_лЬ_й - a₀ ^_v + /Л) + 6₀ (A + A) ’

C; = —a.b, — a₀—b₀ + (А + Я₂ ) (//, + //₂),

С 2 — ^^1 ' ^2 i^X Л^2

где параметры

• <7₀ = 2j2₂ ; a_x = pX_x + (1 - р^Л₂;

^bo = H\M^b_x= qp_x + (1 - qV₂ •

Величины p,XxA2, q, px, p2 являются параметрами гиперэкспоненциальных распределений второго порядка с функциями плотностей ct^A= pAxe л'* +(1 — 7?) Яэе x- ;      (7)

b^t) = qp_xe ^^ + (1 -^) Мг^{е №}'      (⁸)

для системы Н2/Н2/1.

Среднее время ожидания в очереди равно значению производной от функции преобразования Лапласа (5) со знаком минус в точке 5 = 0 . В окончательном виде среднее время ожидания в очереди для СМО Н2/Н2/1 есть

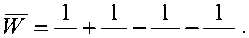
5,    S-, p_x p₂

Выражение (5) на основе свойств преобразования Лапласа, позволяет также определить моменты высших порядков для времени ожидания. Напри- мер, начальный момент второго порядка времени ожидания равен значению второй производной от преобразования (5) в точке 5 = 0 и имеет вид:

^ ₌ d^TAAl ₌ 2. 2   2(5₁₊5₂) _;;

(/5² Ц_ХЦ₂ 5,5₂   //₁//₂5₁²5₂    (10)

x[5i5₂(//i +//₂)-//_1jU₂(5₁ +5₂)].

В свою очередь, начальный момент второго порядка позволяет определить дисперсию времени ожидания. Учитывая определение джиттера в телекоммуникациях как разброс времени ожидания от его среднего значения [4], получим возможность определить джиттер через дисперсию. Это является важным результатом для анализа трафика, чувствительного к задержкам.

Для практического применения результатов (9) и (10) необходимо определить входящие в них параметры, что будет сделано ниже.

Аппроксимация законов распределений на уровне двух первых моментов

Воспользуемся свойством преобразования Лапласа воспроизведения моментов и запишем начальные моменты до второго порядка для распределения (7):

- __; P , (1-7^) .

Л_х 2₂

7.2p 2(l-p)

² 2² A

Рассматривая равенства (11) и (12) как уравнения метода моментов, найдем неизвестные параметры распределения (7) ^i, b₂,p • Для этого запишем связующее условие в виде выражения для квадрата коэффициента вариации

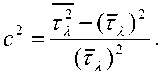
Заметим, что система уравнений (11) и (12) с тремя неизвестными является недоопределенной. Исходя из вида (11), положим

A =^p^x^ ^2 = x\-pWx (14)

и потребуем выполнения условия (13). Подставив выражения (11)-(12) и (14) в (13), решим квадратное уравнение относительно параметра p и полу чим для него два значения:^ = -(1+1^-),

2 у c; +1

причем можно воспользоваться любым из них.

Аналогичным образом поступим с распределением (8). Таким образом, гиперэкспоненциальный закон распределения второго порядка будет полностью определяться двумя первыми моментами и перекрывать весь диапазон изменения коэффициента вариации от 1 до X.

Рассмотрим конкретный пример. Пусть коэффициент загрузки СМО р = т_м!ч = 0,9, где А ^И т , средние значения интервалов между поступлениями и времени обслуживания. В случае нормированного обслуживания Р =^ =1. Тогда средний интервал между поступлениями ^ -Ю/9. Пусть коэффициенты вариаций случайных величин – интервалов между поступлениями и времени обслуживания ^сх = ^с, ^- Аппроксимация на уровне двух первых моментов дает: р « 0,887, Л, » 1,597, Я₂ « 0,203, q~ 0,887, //,«1,775, //₂« 0,225. Таким образом, неизвестные параметры распределений (7) и (8) однозначно определены. Далее воспользуемся результатом для системы Н₂/Н₂/1 (9), приведенным выше: коэффициенты кубического уравнения (6) в этом случае равны с₀ «0,014; с_х « 0,572; с₂ = -0,20. Корни кубического уравнения (8) найдем с помощью пакета Mathcad: - 5, « -0,852, - s₂ « -0,025 , s₃ « 0,677 . Тогда среднее время ожидания, согласно (9), равно W «36,20.

Аппроксимация на уровне трех моментов

Учитывая, что распределение Н2 является трехпараметрическим, аппроксимацию можно выполнить и на уровне трех первых моментов, что позволит сравнить полученные результаты. Для этого запишем выражения для моментов третьего порядка, полученные через преобразование Лапласа:

з 6р б(1-рА

Т 3 — -3--'--3    – для интервалов входного

Х_х Я₂

потока,

“Г 6q , б(1-#)             ~           _

Ъ =-т + ^1   – для времени обслужива-

//, р^

ния. В рассмотренный пример введем в качестве третьего момента коэффициент асимметрии и положим ^sx ⁼ ^А =4 (для пуассоновского потока параметр А =²). При тех же значениях входных параметров СМО начальные моменты второго и третьего порядков для обоих р а спределений , соответствен но , бу ду т равны 5 = 5 (10 / 9)², ?{ = 45 (Ю/9)³, ^ = 5, ^ = 45 .

При таких исходных данных для определения неизвестных параметров входных распределений (3) и (4): (^ ^ Х^ •) р^ (//j >  р^ 5 9) на основе метода моментов запишем две следующие системы уравнений:

JL + b£) = 1o/9;

Я, Я2

Зг+2(1-^) = 5 (10/9)2;

Х\ Л;(15)

^ + fc) = 45(10/9)\

Я, Я9

д ₊ (1-^) ₌ j.

“                  =(16)

⁶ч . 6(1-^)

3 "Г        з, lZ^i М2

решив которые, найдем указанные параметры. Решение системы (15) в пакете Mathcad после округления дает //«0,739; Я, «3,306; Я₂ « 0,294; для системы (16) получаем q «0,739; р_х -3,613; ц_г « 0,327. Определим коэффициенты многочлена (6): с₀ « 0,130; q « 5,172 ; с₂ « -0,40; после чего поиск его корней дает -5, «-2,471, -5₂ «-0,025, 5₃ «2,096. Таким образом, условия для спектрального разложения полностью выполнены: мы получили два действительных отрицательных и один положительный корни. Воспользуемся (10) и определим среднее время ожидания W «37,051. Относительная погрешность в сравнении с результатом аппроксимации на уровне двух моментов составляет 2,35%. При других значениях третьего момента эта погрешность может быть выше. Например, при тех же условиях, но при коэффициентах асимметрии A_sx =A_S^ =10 получим среднее время ожидания W «34,537. Относительная погрешность при этом составляет 4,8%. Этот факт свидетельствует о зависимости результата (9) от моментов третьего порядка.

Разницу между результатами аппроксимации функции плотности (7) на уровне двух и трех первых моментов легко можно проиллюстрировать на рис. 2, так как два подхода разные значения параметров функции (7) Р ? я,, Я₂, что подтверждают приведенные приме ры.

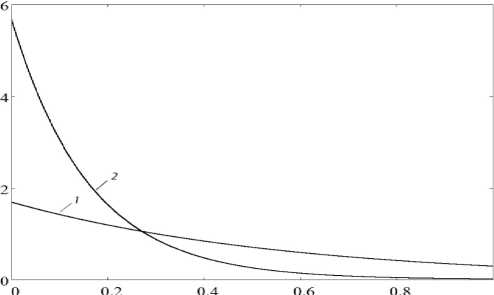
Рис. 2. Графики функции плотности (7): 1 – аппроксимация закона распределения H₂ на уровне двух моментов; 2 – на уровне трех моментов

Решение для системы Н2/М/1

В этом случае функция плотности времени обслуживания имеет вид: , а распределение интервалов поступления остается в виде (7). В работе [2] получено решение для времени ожидания:

W = 1/(7, -1/ ц.

где – корень многочлена с коэффициентами и . Решение для системы Н2/М/1 также существенно зависит от момента третьего порядка, эта зависимость продемонстрирована в [2].

Решение для системы М/Н 2 /1 и его сравнение с формулой Поллячека-Хинчина

В этом случае функция плотности распределения интервалов поступления имеет вид: aQ^ = Яе^ а распределение времени обслуживания остается в виде (8) [2]. Среднее время ожидания

^ _ -1 + -2 Ма + Аз ² А² 2     Ц\Н1

где два действительных отрицательных корня многочлена                 с коэффициентами                                  и есть

-Z. =АК1^-^ТХ^Йй>\

.

После преобразований выражения (18) получим             что полностью совпадает с формулой Поллячека-Хинчина для системы М/G/1 [2]. Заметим, что в этом случае решение не зависит от третьего момента, а полностью зависит от первых двух моментов времени обслуживания.

Заключение

Полученные результаты приводят к следующим выводам.

• 1.    В том случае, когда коэффициенты вариации интервалов поступления < 1 и времени обслуживания < 1, для анализа телетрафика можно использовать систему M/M/1 с запаздыванием.

• 2.    В случае если коэффициенты вариации интервалов поступления больше 1 и времени обслуживания больше 1, можно использовать систему Н₂/Н₂/1.

• 3.    В смешанном случае можно использовать комбинацию рассмотренных законов распределений, что позволит рассматривать СМО с коэффициентами вариаций входных распределений в широком диапазоне от .

• 4.    Рабочие формулы для расчета задержки для первых двух случаев приведены в статье.