Модели теории ползучести бетона и их конечноэлементная реализация
Автор: Гайджуров Птр Павлович, Исхакова Эльвира Рашидовна
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Технические науки
Статья в выпуске: 7 (68) т.12, 2012 года.
Бесплатный доступ
Разработан конечноэлементный метод решения плоской задачи теории ползучести бетона с учётом старения. В качестве наследственных функций второго рода использованы выражения, базирующиеся на формулах для меры ползучести, предложенных Н. Х. Арутюняном и С. В. Александровским. С помощью символьного процессора получены выражения для ядер релаксации бетона, удобные для программирования. Разработаны устойчивый шаговый алгоритм и соответствующая программа, позволяющие выполнять расчёты при переменном нагружении с учётом быстро набегающей ползучести в начальный момент нагружения и частичной обратимости деформаций ползучести при разгрузке. На основе имеющихся экспериментальных данных по ползучести центрально сжатых призматических бетонных стержней и изгибаемых железобетонных балок осуществлена верификация разработанного математического и программного обеспечения.
Метод конечных элементов, плоская задача, наследственная теория старения, численное интегрирование
Короткий адрес: https://sciup.org/14249927
IDR: 14249927 | УДК: 539.376
Текст научной статьи Модели теории ползучести бетона и их конечноэлементная реализация
Введение. В настоящее время накоплен значительный экспериментальный и теоретический материал по ползучести бетона [1, 2, 3]. Вместе с тем известные подходы к расчёту бетонных и железобетонных конструкций с учётом ползучести ориентированы главным образом на решение задач с относительно простой геометрией изделия [1, 3, 4]. В работе [5] приведён конечноэлементный алгоритм решения задачи теории упругой наследственности. Однако данная теория постулирует полную обратимость деформаций ползучести, что ограничивает её применение рамками только «старого» бетона. Поэтому актуальной является проблема разработки более общего конечноэлементного алгоритма, реализующего модель теории наследственного старения, позволяющую моделировать процесс непрерывного бетонирования, а также рассчитывать потерю предварительного натяжения арматуры, обусловленную ползучестью стареющего бетона.
Наследственные функции второго рода для бетона. Физические соотношения для плоской задачи наследственной теории старения запишем в матрично-операторной форме:
где векторы-столбцы напряжений и деформаций {о} = {о11а22а12}г, {е} = {еы е22 2е12}г (Т — символ транспонирования); [Е (t)] — матрица упругости материала; Res = |/?(Г,т)е(/(т)6/т, R(t,T) — ядро релаксации (наследственная функция II рода). Здесь введены обозначения: т — «возраст» материала в момент приложения нагрузки; t — временная координата, отсчитываемая от т до некоторого текущего момента времени наблюдения. Параметры гит измеряются в сутках.
Вид функции R(t,T^ базируется на принятой механико-математической модели ползучести бетона и применяемой функции меры ползучести /9(Г,т). В рамках теории старения выражение для ядра релаксации R(t,T^ имеет вид [1,4]:
/?(f,T)
1 а
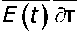
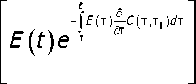
где функция меры ползучести, предложенная Н. X. Арутюняном [2],
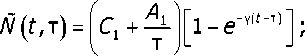
модуль упругости материала E(t) = Ео (1 -е ₽т); Сг, Д, у, Ео, 3 — константы, определяемые из опытов на ползучесть при одноосной деформации. В формуле (1) величину тх можно считать равной моменту времени распалубки. Достоинством представления наследственной функции в форме (1) является то, что после обработки этого выражения в среде символьного процессора компьютерной математики Maple получаем следующую легко программируемую формулу:
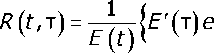
-Е (т) [х3Х2«з (t, т) [д (f, т) Ру - и, (т) у (р + у) + w2 (t, т) у2 ] + +Х2Хз«з (t, т) [щ (f) (3 + У) ~ Д (t, т) У - Ut (т) (3 + у) + w2 (f, т) у]] х ХХ1Х2W3 (t, т) [и, (t ) (3 + у) - Д (f, т) у - щ (т) (3 + у) + w2 (t, т) у]},
где введены обозначения
£'ГТ) - F рт ■ y - е T1(p+v) ■ y - Е Гт С + А V y -____-____
U Г / СоРС z Л1 - с ' Л2 - Г » АЗ - /R , .Л и Гх)-е¥(х+Т1) ■ (t т) - ev(f+T1HT ■ (t т) - e¥'TT'ipf ■ со (t \ / \ \ /
Графики функции R^t,^ для бетона, построенные с помощью формулы (2), для различных значений параметра т приведены на рис. 1. На этом рисунке линиям 1, 2, 3, 4, 5, б соответствует «возраст» бетона (в сутках) 2, 8, 14, 20, 30, 40. Значения констант принимались равными [1]: N, = 9,9388-КГ11 (Н/м2)”1; А, = 4,7095- 10г10 сут./(Н/м2); Ео = 2,55-Ю10 Н/м2; у = 0,03 сутЛ Р = 0,206 сут -1
Всесторонний анализ недостатков теории старения, главным из которых является полное отрицание обратимости деформаций ползучести, представлен в работе [1]. Следующим шагом развития теории ползучести бетона является модель упруго-ползучего тела, или теория наследственного старения. Суть теории наследственного старения состоит в предположении о частичной обратимости деформаций ползучести при условии выполнения принципа наложения воздействий. Наиболее точно экспериментальные данные о ползучести бетона описываются с помощью выражения для меры ползучести, предложенного С. В. Александровским [1]:
С (Г,т) = Ф (т) - ip (Г) — -А + Д (т) 1 - е"0^)]
А А - А
Здесь обозначено: ф(т) = С3+^; Д(т) = Q -С3 + 1 . Величины Д, Аг, А3, Сх, С3, \, о — опытные константы.
Выражение для наследственной функции /?(Г,т), полученное на основе формулы (3), имеет вид [1]:
Ф(т) . е*7 - >42'
№(T)F'(T)(e^-A)-r(T)-[/C(T) xf К hW' hAe^dT + " T4
J \ 7 \ 7 \ 7
---п(т)= f/CMf'Mfe
е
-A^dT,
- А^ (f) - К1 (f)] - о52 (f) + K\t) - E'(t);
М(Г)=А) °3 (JJ
^e(f)[f(f)i(f)]'-o!e’(f)^+|'r'(f)(e,1-^)[e!(f)-'
+2а53(г)Д(г)Л'(г)(е^ -Л2)).
После обработки выражения (4) символьным процессором системы Maple и группировки членов получим следующую формулу для наследственной функции R(t,T^:
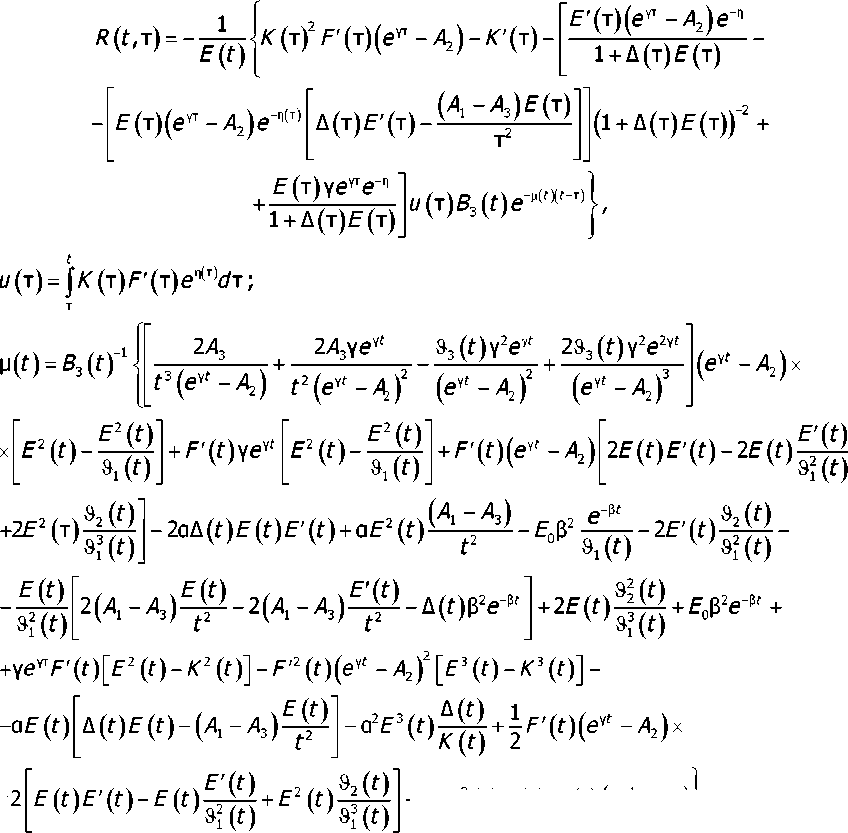
+ 2a53(f)A(f)f'(f)(eYf -Л2) ;
-A А
^ (т) = 1 + Д (т) Е (т); 32 (т) = Д (т) Е' (т) - 1 J; 93 (т) = С3 + ^.
Интегралы п(т) и и(т), входящие в выражение (5), вычисляем численно с помощью формулы трапеций.
Графики функции Я(Г,т) для бетона различного «возраста», построенные на базе формулы (5), показаны на рис. 2. Здесь номера линий соответствуют значениям параметра т (в сутках): 1 — т = 2; 2 — т = 4; 3 — т = 6; 4 — т = 10; 5 — т = 20; б — т = 30. Значения констант принимались равными [1]: ^ = 9,9388-Ю”11 (Н/м2)”1; /V3 = 7,7064-Ю”11 (Н/м2)”1;
А. = 4,7095-Ю"10сут./(Н/м2); А=1; А =3,4822-Ю”10 сут./(Н/м2); 5О=2,55-Ю10 Н/м2; 0=6 сут.”1;
у = 0,03 сут. b Р = 0,206 сут. 1
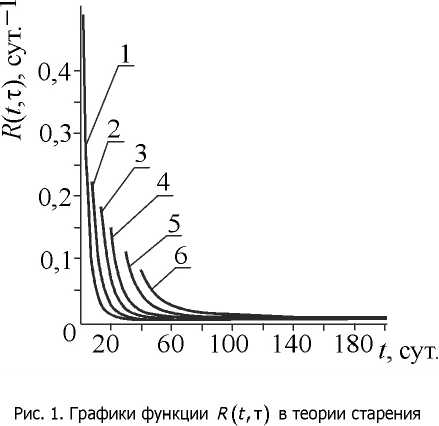
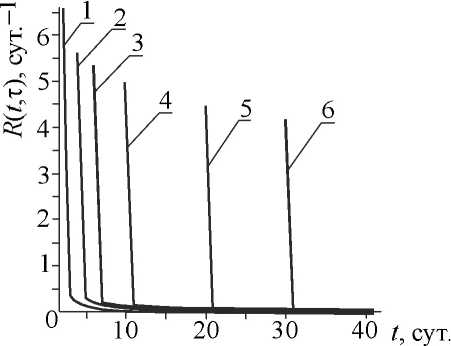
Рис. 2. Графики функции R(t,E) в теории наследственного старения
Отличительная особенность графиков рис. 2 от графиков рис. 1 — резкое убывание функции R(t,T^ в момент времени t = т, что с физической точки зрения отражает наблюдаемое на практике явление «мгновенной» ползучести, условно причисляемое к упруго-мгновенной деформации в момент загружения.
Для описания ползучести «старого» бетона можно использовать теорию упругой наследственности с ядром релаксации типа [1]:
R (t т) — А + А е где Д- = Z^t!(Y4Jo +аАо)[^о(УФ+аДо)-р2] + а2До +у2Ф0}; А = Д0(УФ0 + аД0)-А Pi Р2
1 (
Р1,2 - 2 Г
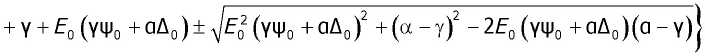
Фо — М3 , До — ^ С3.
Конечноэлементная реализация плоской задачи теории ползучести. Линейно-упругие перемещения в глобальной Декартовой системе осей {ZlzZ2} в произвольной точке конечного элемента (КЭ) задаём с помощью вектора-столбца перемещений {ц) = {у1у2)г ■ Введём векторы- столбцы наследственных деформаций {е}, перемещений {и} и узловых перемещений {й/}: {e} = (1-R){e}, {(7} = (1-R){u}, {H7} = (1-R){iv}.
Векторы-столбцы {е} и {и} имеют структуру, аналогичную {е} и {и}. Размерность вектора-столбца {и/} определяется числом узлов КЭ. Установим связь между {и} и {и/} в виде где [5] — матрица, образованная из функций формы КЭ. Отметим, что для плоского восьмиузлового КЭ матрица [5] имеет размерность 2x8.
В соответствии с принципом возможных перемещений получим операторно-матричное уравнение
[Ar^l-RX^-fr} = 0, (6)
где матрица жёсткости [А'] и вектор-столбец узловых сил {г} КЭ
№ = J [D^ [f ][°]^ , {г} = J ^т {q}dv + J ^т {p}ds ;
Ve Se
{<7} = {<71<72Г' {Р} = {Р1РгГ — векторы-столбцы объёмной и распределённой нагрузки, задаваемой в глобальном базисе; ve — объём, занимаемый КЭ; se — поверхность КЭ, к которой приложена распределённая нагрузка. Матрица [D] для восьмиузлового КЭ имеет размерность 3x16 Выражение [D] для плоского полилинейного КЭ получено в работе [6].
Для вычисления интеграла R{n/} = |/?^,т)^и/(т)]б/т воспользуемся численным методом, основанным на формуле трапеций. Разобьём рассматриваемый временной интервал [т/] на m равноотстоящих временных шагов Lt так, чтобы t = mLt . Тогда выражение (6) можно записать в форме
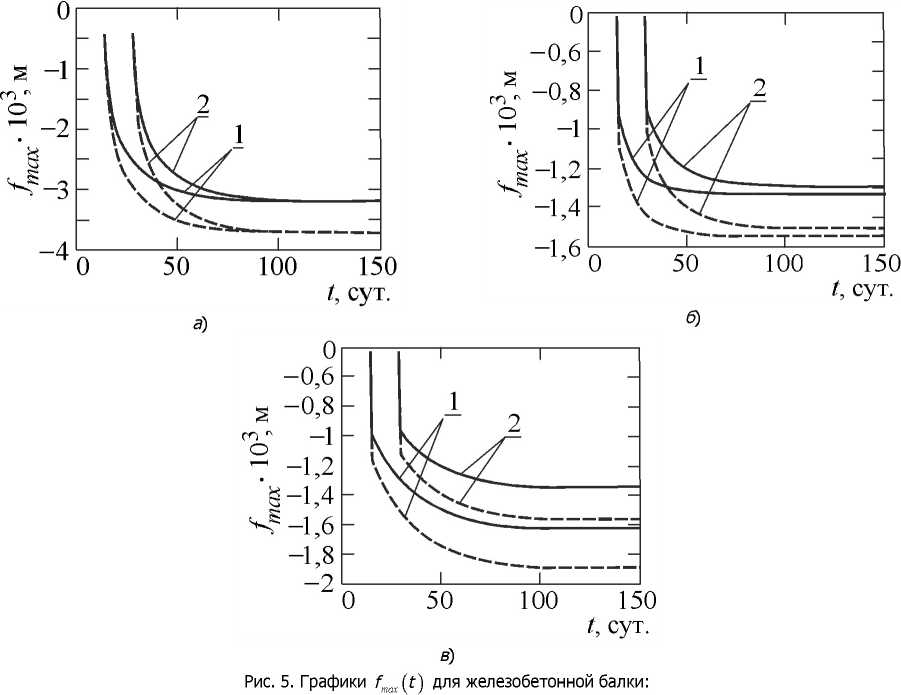
R{kKm}»R(t,t){n 7=1 или в компактном виде К ] К } = И + [^1 >1} +Ц<) ] где [Am] = [A](l -R(f,f)Lt / 2; Щ = [A](l -R(f,T)Af / 2; [А, ] = [А](1 - R(f,(m - j^Lt . В выражении (7) вектор-столбец {и^} соответствует упруго-мгновенному решению задачи. Рассмотренная шаговая конечноэлементная процедура реализована на языке FORTRAN. В расчётных моделях полилинейные КЭ можно ансамблировать с плоскими стержневыми КЭ балочного типа. Числовые примеры. Мгновенное нагружение и последующая ступенчатая разгрузка призматического бетонного образца с размерами 6x6x30 см. Характеристики материала были приведены ранее. «Возраст» бетона в момент нагружения образца — т = 28 сут., момент времени распалубки — Tj = 2 сут. Учитывая симметрию задачи, рассмотрим 1/г часть образца и применим равномерную конечноэлементную разбивку 2x8 (2 КЭ по ширине и 8 КЭ по высоте). Шаг интегрирования Lt принимаем равным 1 сут. График полного перемещения нагруженного торца образца на интервале наблюдения t = 28...200 сут. приведён на рис. 3. 20 60 100 140 180 ^ сут Рис. 3. Ступенчато-убывающий закон нагружения призматического образца: 1 — теория упругой наследственности; 2 — теория старения; 3 — теория наследственного старения Как видно из представленных данных, для модели упругой наследственности (линия 1) выполняется постулат о полной обратимости деформаций ползучести. Для модели упругоползучего тела (линия 3) характерна частичная обратимость неупругих деформаций ползучести, что соответствует результатам аналогичного натурного эксперимента А. Д. Росса [1, 3]. Ползучесть однопролётной железобетонной балки, мгновенно нагруженной сосредоточенной силой посередине пролёта (рис. 4). Размеры балки приведены в метрах. Диаметр арматуры — 8 мм. Модуль упругости арматуры 2,1-Ю5 МПа. Разбивку балки на плоские КЭ выполняем сеткой 6x40 КЭ (6 КЭ по высоте и 40 КЭ по длине). Арматуру моделируем стержневыми КЭ (40 КЭ). Шаг интегрирования — ДГ = 1 сут. Рис. 4. Расчётная схема однопролётной железобетонной балки ^=0,08 Рассмотрим два варианта армирования: I — арматура расположена в нижней (растянутой) половине балки, II — симметричное армирование растянутой и сжатой частей балки. Результаты численного моделирования процесса ползучести в виде графиков зависимости прогиба fmax в центре пролёта от времени наблюдения t и «возраста» бетона т представлены на рис. 5. На рис. 5 штриховые линии относятся к варианту армирования I, сплошные линии — к варианту армирования II; номера линий 1 и 2 соответствуют значениям параметра т, равным 14 и 28 сут. Момент времени распалубки тх = 2 сут. Значения упруго-мгновенного прогиба fmai (т) для вариантов армирования I и II соответственно составляют 0,4890-Ю"3 м и 0,4199-Ю"3 м. Как видно из представленных на рис. 5 графиков, наличие арматуры в сжатой зоне балки обусловливает снижение ползучести для всех реализованных моделей бетона. Вместе с тем только модели теории старения (рис. 5, б) и теории наследственного старения (рис. 5, в) описывают наблюдаемую на практике быстро натекающую деформацию ползучести (т + 1), возникающую сразу после упруго-мгновенной деформации балки. Значения f„,m (t)/f„,m (т) и fmm (f)/A/Л (т +1) где t = 150 сут. для теории старения и теории наследственного старения приведены в табл. а — теория упругой наследственности; б — теория старения; в — теория наследственного старения Значения f (tA/f (т) и f (tA/f (т 11) для однопролётной балки max \ )( max \ ) max у max у / л л ~ Теория (гЖ„(т + 1) т = 14 сут. т = 28 сут. т = 14 сут. т = 28 сут. Теория старения 3,19 3,09 1,44 1,44 Теория наследственного старения 3,87 3,21 1,63 1,39 Из приведённых в табл, данных следует, что значения f„,m (f)/f„,m (т + 1), соответствующие теории старения, для моментов времени т = 14 сут. и т = 28 сут. совпадают. Тогда как в действительности по мере «старения» бетона это отношение должно уменьшаться. Отметим, что данный эффект адекватно описывает теория наследственного старения. Выводы. 1. В рамках теории старения и теории наследственного старения с помощью символьного процессора компьютерной математики Maple получены выражения для ядер релаксации, удобные для программирования. 2. Разработана и программно реализована шаговая процедура метода конечных элементов, позволяющая моделировать процессы последействия в бетонных и железобетонных конструкциях с учётом старения бетона. 3. На тестовых примерах выполнена численная апробация разработанной конечноэлементной программы.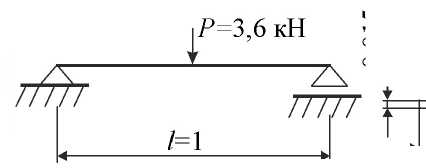
Список литературы Модели теории ползучести бетона и их конечноэлементная реализация
- Александровский, С. В. Расчёт бетонных и железобетонных конструкций на изменения температуры и влажности с учётом ползучести/С. В. Александровский. -Москва: Стройиздат, 1973. -432 с.
- Арутюнян, Н. Х. Некоторые вопросы теории ползучести/Н. Х. Арутюнян. -Москва: Гостехтеоретиздат, 1952. -323 с.
- Улицкий, И. И. Теория и расчёт железобетонных стержневых конструкций с учётом длительных процессов/И. И. Улицкий. -Киев: Будiвельник, 1976. -347 с.
- Прокопович, И. Е. Прикладная теория ползучести/И. Е. Прокопович, В. А. Зедгенидзе. -Москва: Стройиздат, 1980. -240 с.
- Гайджуров, П. П. Конечно-элементное решение задач теории ползучести/П. П. Гайджуров//Строительная механика и расчёт сооружений. -2006. -№ 1. -С. 52-58.
- Гайджуров, П. П. Билинейный четырёхузловой конечный элемент для решения двумерных задач теории упругости/П. П. Гайджуров, Э. Р. Исхакова//Изв. вузов. Северо-Кавк. регион. Техн. науки. -2011. -№ 4. -С. 7-13.


