Модели траекторий нестационарных систем управления с равномерно изменяющимися во времени коэффициентами

Модели нестационарных линейных систем управления с равномерно изменяющимися во времени коэффициентами используются при анализе и синтезе систем управления конечным положением [1-3]. Фундаментальные исследования в области предельной устойчивости систем, которые можно интерпретировать как системы управления конечным положением, опубликованы в работах [4, 5]. Однако в указанных работах рассмотрение ограничивается получением асимптотических разложений интегральных представлений решения задачи Коши, недостаточно удобных для решения задач анализа и синтеза систем управления. В данной работе рассматриваются алгоритмы получения приближенных моделей траекторий, позволяющие судить о зависимости устойчивости и точности таких систем от параметров их элементов не только в конечной точке, но и на всей траектории.

ПОСТАНОВКА ЗАДАЧИ

В работе [1] приведены интегральные представления решения задачи Коши для системы управления с равномерно изменяющейся дальностью до конечной точки траектории по всем координатам системы управления, в том числе — по первой координате, определяющей траекторию объекта управления (1), а также разложение этого интеграла на составляющие, соответствующие особым точкам подынтегрального выражения (2):

c+i l x 1 (t) = ^ f (Wa1 (Р)Fa (Р)ep0

2га J c - i l

^X — 1- j z ^z ^ p( ^{z )d z} ) d Р; Ф ( Р ) L

X

X 1 ( t ) = R 1 ( t ) + R 2 ( t ) + R з ( t ) ,                   (2)

где

m

R 1 ( t ) = -    E

2m v = 1

----1 2 a" X

1 - e -^2na v i k

X J e” • W „( Р ) F a ( Р )

C v -

R 2 ( t ) =

m + m q

= E Re 51

V = m + 1 ^p = z v

1 Ф ⁽ Р )

d р • т J с^{2 т} ф (z)dz , C ^{v +}               V

e pt • W a 1 ( Р ) F a ( Р )

m

R з ( t ) = — E e^ZvT X 2 n i v = 1

X

k Р ^{- z} v

т

Ф ⁽ Р )

Р

^{J e T ( z )d z} [ ,

J e pt • W a 1 ⁽ Р ) F a ( Р ) ^X | + = const

X-----

T v ⁽ Р )

( p - z v ) ^{- e v + 1} 5 3 _V ( p )d p .

/

Там же приведены асимптотические разложения интегралов, входящих в первое слагаемое формулы (2).

Интегральные представления типа (1) и (2), а также асимптотические ряды, используемые для их вычисления, плохо поддаются аналитическому исследованию, недостаточно удобны для анализа и синтеза соответствующих систем управления.

В данной работе ставится задача получения приближенных аналитических зависимостей, пригодных для решения задач анализа и синтеза нестационарных систем управления с равномерно изменяющимися во времени коэффициентами.

Решение этой задачи получим методом приближенного суммирования асимптотических рядов на примере суммирования асимптотических рядов, соответствующих интегральным представлениям (1) и (2).

АЛГОРИТМ ОПРЕДЕЛЕНИЯ ПАРАМЕТРИЧЕСКОЙ ПЕРЕДАТОЧНОЙ ФУНКЦИИ

Рассмотрим теперь алгоритмы вычисления интеграла (1), предусматривающие предварительное вычисление внутреннего интеграла.

Г p ) - J ф ( z )d z

Поскольку ф (p ) = exp

, то, интег-

те

к те 2

рируя внутренний интеграл в (1) по частям, легко получить

1 c + i те

Х|(t)t ■ 10 =      ^ E |(p) + c - i те

+ ept 0 E 1( p )ф -1( p ) J Ф( z )ф( z )dz]dp = те

1 c + i те

= 2П J [ept0E 1(p)х c - i те х (1 + ф-1 (p) • (ф(те) - ф( p)))]dp = c +i

= — J e-F , ( p ) W „( p ) • ^ k-)d p ,       (4)

^{2 n i} c - i те                        ф ⁽ p )

откуда следует, что параметрическая передаточная функция (ППФ) от входа по возмущению, преобразованием Лапласа которого является F , ( p ) , до выхода по первой координате в КТТ (при т = 0 и ф ( те ) =1) имеет вид

T ( p , т )U = W- ( p ) • ^ i ^ ? . (5) ^т ^ ⁰ ф ( p )

Формулы (4) и (5) позволяют, например, вычислить гипотетическое отклонение, которое имела бы траектория снижения летательного аппарата в точке нахождения глиссадного радиомаяка и которое может быть использовано для интегральной оценки точности снижения по заданной глиссаде.

x 1( t ) = c + i те

=— I 2rn c - l те

Г

W , 1 ⁽p ) F , ⁽ p ) e p ⁰ х к

Параметрическая передаточная функция для произвольной точки траектории

p х-----fe ф( Р) те

) ^{z т} ф (z ) d z d p =

2

1 c ⁺ i ”г

= — J [ e^ptE 1 ( Р ) +

2 n i c - 1 те

+ ep‘0 E 1( p )ф -1( p )J epT Ф( z )ф( z )dz]dp, те где E1(p) = W,1(p)Fa (p).

Получение параметрической передаточной функции (ППФ) для произвольного момента времени представляет более сложную задачу. Различные по сложности приближения к точной ППФ получим, используя различные алгоритмы приближенного суммирования асимптотического ряда, в который предварительно необходимо разложить интегральное представление ППФ:

T ⁽ p , ^т ) =

Г

= W , 1 ( p ) • 1 + e к

. - p T

p

ф ^{- 1} ( p ) J e z Ф ( z ) ф ( z )d z . (₆) ^те                        J

Параметрическая передаточная функция для конечной точки траектории

Из формулы (3) следует, что для конечной точки траектории (КТТ), соответствующей т = 0, можно получить

Алгоритм интегрирования по частям

Интегрируя по частям интеграл, входящий в формулу (6), получим асимптотический ряд:

T ⁽ p ^{, T} ) =

W . 1 ( p ) • 1 + e ^{- p т} ф -¹

p

(p)J

У

^W a 1 ⁽P ) ’O ⁺ A ⁽ P^{, T} ) ) =

У e z Ф ( z ) ф ( z )dz

J

чину, имеющую порядок малости первого отбро-

шенного члена асимптотического ряда (7):

^T 1 ⁽ p ^{, т} ) =

= W„( P ) X

= W , 1 ( p ) •

----^T ---+ O ( - т ) + Ф ( p )

f-Ф ^{( p} ) )

X

где

1+^p+-ф( p)+ф 2( p)+о J_)

T               T                V T ..

A ( p , T ) ^ + ^{-ф (} p ) + ^{ф (} p ) + O J_ )

T           T            V Ту

Введем

^ф f p ^{- 5}

^{-ф (} p )Г ^{т у} т ² -Ф ( p ) ф ⁽p )

порядка малости с величиной

² V ^T

J-l

.

— величину одного

^{-ф (} p )

( 5 — ма-

асимптотическое разложение по отрицательным степеням параметра ( т = t - 1 ₀ ) функции

p e - pтф-1 ( p )J ezT Ф( z )ф( z )dz.

те

лая величина, которая может выбираться на основании проведенных экспериментов).

Тогда получим следующее приближение к точному выражению ППФ, которое при т = 0 совпадает с точным выражением (5):

Простейший алгоритм приближенного суммирования асимптотического ряда (7) заключается в замене ряда для A ( p, т ) степенным рядом

^T > ( p ^{, т} ) =

f ф p

У

5 )

+---

(- т и

W , 1 -Ф ( p )

ф ⁽ p )    ( ^{- т} ) ^{+ ф} ( p )

A 1 ( p , т ) = '^p ' +—(^ + O — .       (8)

т т 2 V т 3 J

Полагая A ( p , т ) - A 1 ( p , т ) , для T ( p , т ) получим асимптотический ряд

Формула (11) для больших т позволяет моделировать поведение первой координаты функцией, проходящей через начальную и конечную точки траектории и зависящей от всех параметров системы управления.

T ( p , T ) - W „( p ) •

1 + Ф(p) + 52(p) + T T

который формально совпадает с в виде ряда дроби

представлением

_T\ = ^W"^{1( p} )

T ^{1 ( p , T} ) 1 + Ф ( p ) "  ^{( - T} )

Выражение T ( p , т ) может рассматриваться как аналитическое продолжение в область интере - ^ф( p )

сующих нас значений ---- асимптотического

( - T )

ряда (7).

Ряд (8) получен отбрасыванием из асимптотического разложения (7) всех производных передаточной функции Ф ( p ). В результате при т = 0 передаточная функция (9) отличается от точного значения (5).

Для обеспечения совпадения при т = 0 формул (9) и (5) прибавим к передаточной функции вели-

Алгоритм разложения подынтегральной функции в ряд Маклорена

Ввод дополнительного слагаемого в формулу (10) скажется только при очень небольших значениях (- т ), поэтому исследование поведения решения распадается на два этапа: на этап, соответствующий т =0, и на этап, соответствующий т ^ 0. Такое раздельное рассмотрение одного и того же решения не всегда может оказаться достаточно удобным. Поэтому целесообразно рассмотреть и другое разложение функции:

p

A (p, т) = e - pтф-1 (p) J ez Ф( z )ф( z )dz = те

p

= e - ^{p т} ф ^{- 1} ( p ) • т J e^{z т} ф ( z )d z - 1 .             (12)

те

Статическая система управления. Предположим вначале, что функция ф ( z ) не имеет особой точки в нуле (соответствует статической системе управления). Тогда подынтегральное выражение в A ( p , т ) разложим в ряд по положительным степеням z и проинтегрируем этот ряд по частям:

p

Т J ezтф( z )dz = те

(

A ⁽ p , ^т ) = ф ⁽ p ) ' ф p

к

-11

^{т J}

- 1 ;

p

( z

= т J e  ф(0 +1! ф(0) + те ^

Z2

—ф (0) + - d z ;

²"             ^J

T 3 ⁽ p , ^т ) = W ⁽ p ) ' ^{( 1 +} A ⁽ p , ^т ) ) =

;

( ф p

f e^{z T} ф (0)d z = ^ e p ;

J                         7"

те

-11 _а!

= W , 1 ( p )        .

ф ⁽ p )

.

p

J«”ф> (G)-dz = те

i^ e P ( p - 1 1

^T I ^{T J}

Pf e^{z T} ф (0) — d z = Ю e^{p T}

^J 2! t те

2!

(

P

к

-

2P +

7"

I

^{T J}

.

Таким образом, для статических систем управления имеем

p т J ezтф( z )dz = те

p

= т J e”

те

= e^{p T}

p

-

+

к

z

ф (0) + - ф (0)

+ ^z i (0) + - d z - 2^{! J}

1 ^p — i (0) +    _|( ^T ф (0) +

1 I ²

T

J

2!

P (0) +

(

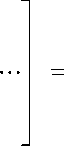
= epтф p -к

7"

J

Астатическая система управления. В случае астатической системы управления функция ф (z ) имеет особую точку в нуле, однако вначале можно сдвинуть эту особую точку вдоль отрицательной полуоси на небольшую величину, получить аппроксимирующее выражение (13), затем вернуться к истинному представлению функции ф (p ) . Так будет выполнено аналитическое продолжение функции (13) на случай астатической системы управления. Подставляя приближенное выражение (13) в формулу (12) и (12) в формулу (7), получим:

Как показали результаты моделирования, при 1 ₀ <  20 с более точна формула (14), а при 1 ₀ >  20 с — формула (11).

Как следует из формул (11) и (14), анализ устойчивости и синтез оптимальных управлений применительно к области, непосредственно примыкающей к КТТ, не может быть выполнен обычными методами теории стационарных систем управления, поскольку параметрическая передаточная функция в указанной области в общем случае содержит точки ветвления, т. е. не является целой функцией.

Модели (11) и (14) ППФ могут послужить основой для разработки методов анализа устойчивости и синтеза оптимальных систем управления, передаточные функции которых содержат точки ветвления типа ( p - z _v ) “ ^v , где a_v — нецелое или комплексное число. Далее будем пользоваться формулой (14) как более компактной и ориентированной на не очень большие начальные дальности маневрирования.

АЛГОРИТМЫ ВЫЧИСЛЕНИЯ ВСЕХ СОСТАВЛЯЮЩИХ РЕШЕНИЯ ЗАДАЧИ КОШИ

Рассмотрим алгоритмы вычисления всех составляющих, входящих в формулу (2).

Вычисление R ₁( t )

Обозначим:

F_t( p ) = W „ , ( p ) F , ( p )4^ = E 1 ^{( p} r ; ф ⁽p )    ф ⁽p )

J 1 v ⁽ t g) = J ^{e pt 0 (} p ^- z v ) ^av - ^Pv F 1 v ⁽ p )^d p ;

ф (.-) = ( z - z v )"* ф v ( z ) ;

F , ( p ) = ( p - z v ) ^{av - Pv} F . v ( p ) ;

J 2 v ( ^T ) = J e^{z T} ( z ^- z v ) "^av Ф v ( z )d z .

C v +

Тогда

1 m.      1

R ^{1 (} t ) = - п ^X 1 - e -^J ^{1 v (} t " ^T " J ^{2 v ( T} ) •

В [1] показано, что интеграл J _{1 v} ( 1 ₀) может быть представлен в виде асимптотического разложения по отрицательным степеням 1 ₀

J v (10) = —2ze" 01 o“v + Pv' x xsinn(a - pv + 1)r(av - Pv +1)5„(t0),

где

5 1 v ( 1 0 ) =

= y ( - 1) ^k

0 = 0       F ( a , -

^{- p}v ^{+ k + 1)}

Fv(0)-X k=1

1 k !

те

Fv (0)+Х k=1

= F v

d k

FT F ⁽ Р ) d p

k !

x ( - 1) ^k

Р = 0

dk к „ "ГТ FV (Р) Pv +1)" 10 " k! [dpk

Г ( z ) — гамма-функция.

J p = 0

С точностью до величин порядка малости — t ₀ верно приближенное равенство

^{( a}v ^{- p}v ^{+ 1)} ^ ^{( a}v ^{- p}v ^{+ k} )

d k F ^f - ^av - ^Pv - ¹ '

L1

f ^d

L

^{- a}v ^{+ p}v

- 1 ) ^k

x ( - 1) ^k

^{( a}v ^- P v ^{+ 1)} k k

t ₀

1

^- « v ⁺ P v ^{- 1} = 0

t 0

^f- « v ^{+ P}v ^{- 1} )

L

t ₀

1

Поэтому интеграл J _{1 v} ( 1 ₀) может быть прибли-

5 2 v ( т ) =

женно вычислен по формуле

^J 1 v ⁽ t 0 ) ~

те

= r(-«v + 1)X k=0

= - 2 ie^{z t 0} 1,

- « v + P v

- 1

sin n ( a_v

-

P v ^{+ 1)} t 0 - ^{1 x}

xr ( « v

-

P v + 1) "  F 1 v

-

«v + Pv

-

A

k

^{D 2 v )( Z} v ) = d “ T ^

^{( 1)} D<^k)

2 v ^{( z} v ) k !

f u ^

r(-av + k +1) r(-av + 1)(-т)k ’

-

2 nz'

e^{zv 0} 1,

-a v + P v

- 1

L

V

^L - ^{т 1} J u = 0

.

^{r ( - a}v ⁺ P v )

• F

F 1 v

-

L

t ₀

1

^av ^{+ P}v

t ₀

В соответствии с работой [1] имеем

J 2 v ( т ) = e^{Z vT}

( - Т ) “ • ¹ J

e

-M uu

-« v

-

A

. (15)

1

u фv — du =

= e^{Z vT}

( - т ) ^a v ^{- 1} ( e " ^{2 na} v i

C 0+

-

1 ) 5 2 , ( т ) ,

L

-

т

1

где

Ряд 5_{2 v} ( т ) является асимптотическим по т рядом, пригодным для вычисления интеграла J _2v ( т ) при больших т .

В случае, когда a_v >1, интегрированием по частям можно получить

J e “ u

^C 0+

^-a v

f U ф_v — d u =

L-т 1

= J e - • “

C 0+

-« v ⁺ r₂ v 1

-

L

г Г du 1

f “

Ф v — d u ,

^{L- т 1}

D , ⁾ (z , ) =

d *

d и *

1 -

. к

г Г d u J

Ф ,

f и А

^{к т} /JJ и = 0

сходится равномерно во всех точках промежутка 0 < t < 10, интеграл J20, (т) можно разложить в ряд Тейлора в окрестности точки t = t* < 10:

где г₂ , = [ а , ] — целая вещественная часть числа

J20, (t) = J20,0(т*) + а, ■

С точностью до величин порядка малости

-—— имеет место приближенное равенство

+ J20,1 (т*) ■ (t - t*) + J^т^ ■ (t - t*)2 + ..., где

^ 2 , ^{( т )} = ^{Г ( - а}, + Г , + ^{1) Х}

^хУ ^ 5 D 2 , ' (z , X-D * к = 0 * ^!

( -а , )-( -а , + к ) ( - т ) *

~Г(-а, + г2, +1) х

те

хУ '

I к !

d * D 2 ,4 ² ,

+

—S а, ) -т

— \* d ^f ° - ^{к- т} )

= Г ( - а , + г , + 1) ■ D 2 , ⁾

f ^z ,

к

•- а ,

-т

( а — ) * г ■-------- т

( - т ) *

•

+ ° А

^{- т 7}

-—.

где ^а, = ^а, ^{- г} 2 , .

При достаточно больших значениях (- т ) инте-

грал J ₂ , ( т ) может быть записан более

компактно

J 2 , ^{( т )} = j ^Ф ^{( Z )d z} =

C , +

= в² , ^т ( - т ) ^{а 1} ( е ^п - 1 ) х

хГ ( - а , + г 2 „ + 1) D 2 ,>

f а А

Z , + — .

к

-

т7

^J 20 , * ^{( т} *⁾ = J ^{eP T} P "“ ^, ■ Ф , ⁽ P ⁺ z , ^)d P ,

C 0

т * = t * - 1 0 , * = 0, 1, 2, 3,^.

Интегралы J₂₀ , * ( т *) для достаточно больших абсолютных значений т * могут быть вычислены с использованием формулы (16).

Обобщая полученные результаты, можно написать окончательное выражение для R 1 ( t ) :

R 1 ⁽ t ⁾ =^{-    x}

2 n z

m

хУ

1 - _e -^гпа v ⁱ

m

-у

Х F ,

J e^{p t 0} F1( p )dp ■ т J е^{2 т} ф (z )d z =

C , -

C ,

e^z ^ Г ( - а , + г , + 1)  ( - т ) ^-

^{г ( - а}, ⁺ p , ⁾

f - а, + p,

-

1А

( 1 ₀) ^а , " ^p , ^{+ 1}

Х

к

t ₀

7

(0) 2 ,

f ^{Z v}

к

—•

+а,)

-

т 7J

,

где о с , = а , - г ₂ , — дополнительная к целому числу часть показателя а , особой точки ( z - z , ); г ₂ , = [ а , ] — целая вещественная часть числа а , .

При малых значениях   (- т )   интеграл

J 2 , ^{( т )} = J e X ^z)dz C , +

можно представить в виде

J 2 , ^{( т )} = J ^{e Z T} Ф ^{( z )d z} = e" ^J 20 , ^{( т )} ,

C,+ где J20, (т) = J ep(t-t0)P~аV ■ Ф, (P + z , )dP .

C 0+

Поскольку интеграл

J _{20 , *} ( т ) =

= J |т e p ⁽ t - t ^{0 )} P "° ■ Ф , ( P + z , )d P

C 0

Вычисление R ₂( t )

Основная трудность вычисления R ₂( t ) связана с вычислением выражений

т

Ф ^{( z} , ⁾

z ,

J е2тф( z )dz те при значениях z, = z,-, соответствующих полюсам функции F1 (P) , не совпадающим с особыми точками функции ф(P).

Воспользовавшись формулой (13), можно получить

(      1A zv               е'-ф |zv — -

—— J ^{eZ T} ф ^{( z )d z} =---

Ф ^{( z} v ) L                  Ф ^{( z} v )

.

Следовательно,

R 2 ( t ) =

m + mq.

I -

получим, подставляя в формулу (3) выражение для передаточной функции (6) и полагая T ( P , т ) =

= ^T 3 ⁽ P , ^т ) :

^x 1 ⁽ t 0 )

—

2 n i

c + i l

J e^ptT ( p , т )d p = c — i l

= X Re -- • W. 1 (p ) f , ( p )

т

v = m + 1

P = z v

• v

Ф ⁽ P )

p

L

с^2т ф (z )d z - .

—

И таким образом,

i c + i l

2 - ; J e - F , ( p ) W „( p ) • c — i l

Ф p

1 ^

—

k

T

Ф ⁽ P )

^J d p =

R 2 ( t ) =

m + m_q.

-

= X e^W .» ( P ) F „ ( P )

v = m + 1

Г

Ф z. k

1 ^

_^J

Ф (Z v )

.

—

m

X J e^ptF - ( P ) W „( P ) • 2 n z

C v —

Ф P

1 ^

—

k

т

Ф ⁽ P )

^J d p

—

Вычисление R ₃( t )

—

Эта задача решается по правилам вычисления вычетов

m

X

2 ni v = 1 c

^C v

Ф P

1 ^

—

т

e^PF , ( P ) W - , ( P ), Ф ⁽ P )

J

dp +

+ —

R з ( t ) =

2 nz'

m

X   J l e^P ' F .v ( p )W„„ ( p ) x

p — z v |+= const

= - £ P z v T x

2 n i

Ф P

1 ^

—

x

k

7"

^x 1 e^P t ⁰ E 1 v ⁽ P )

I P — z v | ₊ = const

Ф v ⁽ P )

⁽ P ^— z v )

— I

q ^v ■ • ' S 3 v ( P )d p ].

Ф v ⁽ P )

^{2 (} P

—

zv

) ^{— q v +} ] d p +

И тогда

R з ( t ) =

m

= X e

, ^z v t

—

k

d dzv

k q v +

— 2

—

J

E „( z , ) S (^z '

Ф v ⁽ z v )

.

Здесь обозначены:

0 < k < q v + — 2

S 3 v ( P ) =   X D 3 v . ( т )

k = 0

( P — z v ) * ; — Q v + k + 1

E 1 ( P ) =

= ( z — Z v ) ^{av — pv} E l ( P ) =

= ( z — z . ) ^{av — pv} W - ( P ) F -v ( P );

D v k ( т ) = ¹ k !

Lk

d d P

—

) k

^T Ф v ⁽ P )

J

^J P = zv

.

Приближенное интегральное представление решения задачи Коши при любых значениях (- т )

+--

2 n i

Ф v т

x

m

X    J [ e^Pt F„. ( P )W „ , v . ( P ) x

^{v т 1} P ^{— z} v.

₊ = const

p

—

k

Ф ⁽ P )

m + m_{q —}

+ X ezvt v= m +1

x

1 ^

7"

k

⁽ P ^{— z} v_T

) ^—+ ] d p +

d dP

q v — ^{— 1}

^— t

J

x

F , ( p ) W , 1 ( p ) •

(     1 ^

Ф P — -k     т^

Ф ⁽ P )

P = z _v

В соответствии с формулой (15) для общего случая (относительно значений a_v и p_v ) будем иметь

m

—£ e^^x , ( p )d p

2т Vic

C v -

от общих формул проявляются в вычислении интегралов вида

m £ V = 1

- v t -- a v + P v - 1 et       _D

^{r ( - a}v ^{+ p}v ⁺ r l v ⁺ 1)

( ^-av ^{+ p}v ^{- 1} )

r 12

к

t

2

где r1v = [ Pv - av -1] — целое неотрицательное число, ближайшее к вещественной части числа (pv - av - 1) или нуль;

J 1 v ( t ) = -^ J e-E 1 ( p ) ^C v -

d p--

—^k---d p

d ⁽ p )

D v ( Р) =

. к

г - t Т ^d p J

X 1 v ( Р )

X 1 ( p ) = F . ( p ) W . 1 ( p ) •

Г 12 dp - к ' 2

d ⁽ p )

^J 2 v ^{( T} ) =  ---1^7 J e z ^{T d (} z ) d z =

^{1 -} e        C _{v +}

= e--' (-T)av -1 D2;>r Zv +       , k - T 2

где

E 1 ( p ) = F . ( p ) W . 1 ( p ) ;

a_v , p_v — целые числа; a_v - p_v <  0 ;

X 1 v

' " ^a v ^{+ p} v " ¹ '

^к t ²

d

r 12

p

= F .v

^{- a}v ^{+ p}v

- W.

X

E 1 ( p )     Г A

d ( p )

T

-2 =

-

X

к

av + p

v

t

2

^{/- a}v ^{+ p}v - ¹

1__________ t_________

11

T

r 12

d p - -

= ⁽ p ^- z v ) ^av " ^{pv E} 1 v ⁽ p ) ^к . d v ⁽ p )

'"av + pv - 1 '

^к t ²

В случае если в точке p = z _v подынтегральная

функция имеет полюс порядка q _v , интеграл

J e^ptX , ( p )d p вычисляется по формуле вычетов

^C v -

В этом случае можно воспользоваться формулами (15) и (16) для вычисления интегралов J _{1 v} ( t ) и J_{2 v} ( t ) при нецелых a_v , а затем перейти к целым значениям a_v . В частности, интеграл J _{1 v} ( t ) при a_v - p_v <  0 может быть представлен в виде конечной суммы

J e-X 1 ( p )d p =     J e-X 1, ( p )( p - Z v )" * d p =

C v -                          p - Z v |₊= const

J _{1 v} ( t ) = ——2 ie^{z v} t"^{a v + pv 1} X

2 n i

= e z ^v t

к

d d p

k q v ¹

- t    X 1 v ( p )

2

X sin n ( a v - p v + 1) r ( a v - p v + 1) S ' - ( t ),

где

где     q _{v +}

порядок полюса

функции

r 12 dp --

T

^X 1 ⁽ p ) = ^F . ⁽ p ^)W . 1 ⁽ p i          ' в точке p = z v •

d ( p )

p v - ^a v

S 1v (t) = £ k=0

( - 1) k X

_X ^{r ( a}v ^{- p}v ⁺ k ⁺ 1) r ( a v - p v + 1) • t^k . k !

d ^k

^E - ⁽ u ) d u ^k

u = 0 J

ВЫЧИСЛЕНИЕ КОНТУРНЫХ ИНТЕГРАЛОВ ПРИ ЦЕЛЫХ СТЕПЕНЯХ ОСОБЫХ ТОЧЕК

Поскольку

При целочисленных показателях степеней особых точек подынтегральных функций отличия

sin ⁿ ( ^av ^- p v ⁺ 1) ^r ( ^av ^- p v ⁺ 1) = —--------Г,

r(-av + pv)

то при a_v - p_v <  0 функция (21) не равна нулю.

Если a_v - p_v >  0 , функция (21) и интегралы

J _{1 v} ( 1 ₀) , J _v ( t ) равны нулю.

Обычно a_v > 1, поэтому интеграл J_{2 v} ( t ) может быть представлен в виде конечной суммы

^J 2 v ^{( T} ) =

e z ^v ( -T ) ^{a - 1} D 2 v

( a A Zv + — ,

k

-

^T )

где

D 2 v

zv

—

+ Ov.)

k

-

T J

-

d A ^av

Lk

dz v

P v ⁽ z )

^— a .

v

-I Z = Z v +---

-T

a v

= 2 (-1) kC k=0

, k d ^{O v} ^ v ( Z ) ^av   d Z ^av

.

—— ^a z = Z v +--

- T

Формулы (21), (22) позволяют моделировать переходные процессы для целых значений показателей степеней особых точек подынтегральных выражений, встречающихся в решениях задачи Коши для системы линейных нестационарных дифференциальных уравнений с равномерным по времени изменением коэффициентов дифференциальных уравнений.

При выводе формул (9), (11) и (14) не предполагается предварительное вычисление параметров ( Z _v , a_v ) особых точек подынтегральных выражений, поэтому соответствующие этим формулам аналитические модели могут быть отнесены к бес-корневым методам аналитического моделирования.

Формулы (17)–(20) представляют собой приближенные выражения для интегралов, входящих в решение задачи Коши для рассматриваемой нестационарной системы. Аналитические модели по формулам (17)–(20) могут быть построены только после нахождения аналитических зависимостей параметров ( Z _v , a_v ) особых точек подынтегральных выражений от параметров системы управления. Соответствующее направление моделирования может быть отнесено к корневым методам аналитического моделирования.

в работе [1] для всех интегралов, входящих в структуру решения задачи Коши для рассматриваемой в работе системы линейных дифференциальных уравнений с переменными во времени коэффициентами. Впервые получены алгоритмы приближенного суммирования асимптотических рядов, позволяющие построить приближенные аналитические решения рассматриваемой системы дифференциальных уравнений с переменными коэффициентами, учитывающие значения точного решения в начальной и конечной точках траектории.