Модели управления портфелем ценных бумаг

Основная задача при формировании портфеля распределить денежные средства так, чтобы цели инвестора были достигнуты. Инвестор в первую очередь стремится получить максимальный доход за счет изменения курсов акций, дивидендов, получения процентов. С другой стороны, любое вложение средств сопряжено с опасностью «утери» денег, следовательно, нужно сформировать портфель ценных бумаг так, чтобы минимизировать данный риск, для этого нужно воспользоваться моделью формирования портфеля.

Рассмотрим модели формирования портфеля.1.    Модель Марковица.

Основной идеей модели Марковица является то, что доход является случайной величиной, то есть он изменяется в некоторых пределах по отдельным инвестиционным объектам. А значит, если определить вероятности наступления инвестиционных объектов, то можно по каждому виду вложения средств определить распределение вероятностей получения дохода. Это является вероятностной моделью рынка. Модель Марковица предполагает, что доходы распределены нормально.

Модель Марковица определяет риск и количество инвестиций, что помогает инвестору сделать выбор между разными вариантами вложений капитала исходя из поставленных целей.

Формула математического ожидания имеет вид:

^mi ⁼ S=l^i * ?ir

^ - возможный доход no i- ценной бумаге, руб.;

Pg - вероятность получения дохода; п — количество ценных бумаг.

Показатели рассеивания измеряют величину риска. Следовательно, вероятность, что ожидаемый нами доход будет выше, если разброс величин возможных доходов невелик. Среднеквадратическое отклонение является мерой рассеивания.

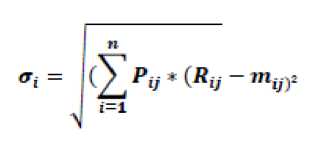
Параметрическая модель, в отличии от вероятностной, может допустить эффективную статистическую оценку, исходя из статистических данных параметров этой модели за прошлые периоды. Ряды доходностей за последовательные периоды в прошлом являются этими статистическими данными.

2.    Модель Блека.[1]

Главное отличие модели Блека от Марковица заключается в том, что инвестор может продавать активы, предоставленные ему в качестве займа, другими словами осуществлять короткие продажи. Инвестор «делает ставку» на снижение стоимости ценной бумаги, чтобы потом отдать заем этой же ценной бумагой, но по сниженной цене. Таким образом, возможная прибыль не ограничена максимальной доходностью одного из активов, так как нет ограничения на долю активов в портфеле.

3.    Рыночная модель Уильяма Шарпа

Для небольшого количества ценных бумаг рассчитать математическое ожидание, ковариацию между доходностями, среднеквадратическое отклонение на практике вполне возможно, однако расчет коэффициента корреляции может вызвать затруднения.

Предложив индексную модель Шарп снизил трудоемкость расчета. Шарп нашел способ поиска приближенного решения с гораздо меньшими усилиями, он ввел фактор β, который является измерителем риска.

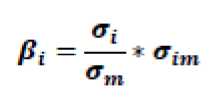
o^ - ковариация между темпами роста курса ценной бумаги и темпами роста рынка;

Oj - стандартное отклонение i- того актива в портфеле, ат - стандартное отклонение доходности по рынку в целом.

Показатель β показывает во сколько раз изменение стоимости ценной бумаги отличается от рыночной стоимости, то есть характеризует степень риска бумаги. Если β > 1, то цена бумаги движется в среднем быстрее рынка – инструмент с повышенным риском, если β < 1, то в течение периода расчета цена бумаги в целом изменялась медленнее, чем рыночная – степень риска низкая, если β < 0, то изменение стоимости ценной бумаги было противоположным движению цены на рынке.

Модель Шарпа предполагает, тесную корреляционную связь между изменениями отдельных курсов акций, а значит, все входные данные, которые необходимы могут быть определены базисным фактором и отношений, связывающих его с изменением курсов отдельных акций. Чаще всего такой фактор берется из индекса. Доходность ценной бумаги, зависима от индекса описывается:

ri = ai+pi *r + si (7)

n – доходность i – той ЦБ за период, ai+fii – константы, характеризующие i – тую ценную бумагу, – индекс рынка, El – независимые случайные величины.

Из уравнения следует, что P является наклоном линии. При постоянной p («исторической») можно оценить сопоставляя данные о соотношении доходностей за прошлые года с доходностью рынка. Таким образом, при расчете коэффициента p он имеет вид линейной регрессии или метода наименьших квадратов.

Так как уравнение выше написано без случайной погрешности, то оно является уравнением линейной регрессии, а значит параметр p это коэффициент регрессии и определяется формулой:

11                       11           11

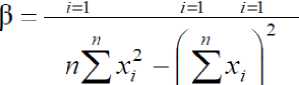
7=1 К 7=1   7

xi, yi – доходность рынка в i – той период времени;

n – количество периодов.

Для достижения наилучшего эффекта на различных стадиях развития рынка используются следующие комбинации коэффициентов:

Таблица 2

Комбинация коэффициентов регрессионного анализа

Состояние рынка

На покупку

На продажу

• •    1. Падающий рынок

• •    2. Растущий рынок

• •    1. р<0. p2^0

• •    2. р>0. p>l.a<0.R²^0

• •    1. р>0. a>0.R²^0

• •    2. р0.R²^0

4.    Модель Тобина – Шарпа - Линтнера [1]

Модель Тобина, в отличие ото всех предыдущих, относится больше к структуре рынка, а не портфеля. В этой модели используются безрисковые ценные бумаги (государственные или вклады в банках). Дж. Тобин показал, если построить прямую по формуле

(9) где f- безрисковый актив, а Θ = (pi…pn) является некоторым портфелем (pi – доля актива в портфеле), то среди портфелей лежащих на прямой нужно выбрать тот, который касается эффективного множества в наиболее высокой точке.

М.: Издательско-информационный дом «Филинъ», 1998.

"Экономика и социум" №12(43) 2017