Модели взаимодействия в производственной системе и организация условий сбалансированности выпуска продукции в заданном соотношении

Описание производственной системы крупного промышленного комплекса по производству сложных наукоемких изделий включает в себя снабженческо-производственно-сбытовые подсистемы, каждая из которых обладает организационно-техническим потенциалом, являются объектом осуществления инвестиционной деятельности, направленной на повышение эффективности, конкурентоспособности функционирования предприятия. Снабженческо-производственно-сбытовые подсистемы, должны обеспечить оптимальную сбалансированность между материальными потоками, затратами в сбытовой, производственной и закупочной деятельности. В работе особое влияние уделено методам и механизмам организации и управления в решении задач комплектной поставки продукции. Рассмотрим подсистему «заказчик - поставщики», в которой заказчик является административным органом, имеющим право устанавливать управление и план в каждом периоде функционирования. Кроме того, заказчик имеет право проводить «координацию системы» с целью повышения эффективности управления. При этом заказчик при необходимости имеет возможность осуществлять координацию системы с целью реализации плановых заданий.

Пусть производственная система характеризуется фактическим состоянием поставщиков У = {у J, У е Y, где Y – множество допустимых состояний производственной системы в целом(УсЩ=1УЭ. Плановое состояние производственной системы определим как совокупность планов выпуска продукции поставщи- ками х = [%J. Пусть, множество реализуемых планов производственной системы X совпадает с множеством ее возможных состояний Y.

Целевая функция заказчика W = Ф(Л, х, у) удовлетворяет условию

Ф(Л, х, у) < Ф(2,у, у), если х ^ у , (1) что соответствует потерям в системе при несовпадении плана и реализации.

Исследуем производственную систему «заказчик - поставщики» в условиях независимости между поставщиками в процессе производства продукции. В производственной системе с независимыми поставщиками при установленном плане x_i , поставщики могут выбрать реализацию y_i , из некоторого множества B_i ( x_i ) независимо от других поставщиков. Возможность такого выбора требует определенных ограничений на план x , удовлетворяющих условию

п

В(х) с Y, где В(х) с j^ В^х^. (2) i=l

Из (2) следует, что любой выбор реализации У( е в^ обеспечивает реализацию системы ye Y. Множество планов x , удовлетворяющих (2), обозначим через Z . Это означает, что в системе с независимыми поставщиками устанавливаемые заказчиком планы х е z .. Приведем несколько примеров производственных систем с независимыми поставщиками.

МОДЕЛИРОВАНИЕ

ВЗАИМОДЕЙСТВИЯ МЕЖДУ СУБЪЕКТАМИ В ПРОИЗВОДСТВЕННОЙ СИСТЕМЕ

Пекина Ксения Александровна, кандидат технических      Рассмотрим механизмы организации сбалан- наук.                                           сированного взаимодействия в производствен-

ной системе «заказчик - поставщик» по выпуску продукции в заданном соотношении, состоящую из заказчика и n поставщиков, каждый из которых может выпускать комплектующие изделия m различных видов. Обозначим T_i – продолжительность планируемого периода i -го поставщика, x_ij – продолжительность работы поставщика i по выпуску продукции вида j , a_ij – максимальный выпуск продукции j -го вида i -м поставщиком за единицу времени (реальный выпуск может быть меньше этого максимального при плохой организации производства, наличии простоев оборудования и т. д.). При заданном управляющем воздействии равном объему выпускаемой продукции с позиции заказчика x = { x_ij }, продукции вида j будет выпущено Zy <    ’ CL[jXij .

i

Поставим задачу определения максимального выпуска продукции в заданном отношении B₁ : B₂ : ... Bm . Модель задачи имеет вид:

модель целевой функции заказчика

Ф(г) = min--> max j Bt x при условиях Хц > 0

^Xi^^iT-.^Ti.i^Vn.

Для оценки уровня сбалансированности материальных потоков в организационной системе, примем в качестве целевых функций поставщиков, объем реализованной продукции (предполагаем, что вся произведенная продукция будет реализована)

fMzt) = I.^AjZij i = l,n, где λj – цена продукции j-го вида. При заданных λ целевая функция является строго возрастающей функцией zij, поэтому zij = aij xij и m fM,z^ = фДзд) = ^Ajaijxij,i = l,n.

7 = 1

Предположим, что на цены продукции нало-m жены ограничения У AjBj = c , где c – цена комплектного набора {Bj} . Соответственно целевая функция заказчика при подстановке zij = aij xij

Ф(г) = Ф(х,а) = min;^p=1 aiyxiy.

Обозначим {sj} оценки коэффициентов {aij} , сообщаемые поставщиками заказчику. Примем, что d < stj < D (d > 0, D < oo) . Исследуем эффективность сбалансированного взаимодействия между заказчиком и поставщиками. С учетом введенных обозначений целевая функция i-го поставщика имеет вид

m

Hi (Л, Xi, ai) = ^ AjSijXij -» max, i — l,n. (3) j=^

достигает максимума на множестве возможных планов -го поставщика

m

^ Хц = Т_ь i = 1, n, x^ > 0, i = 1, n,     j = 1, m (4)

в точке { x_ij } вида x_ik = T , x_ij = 0 для j ≠ k , причем ^•k^tk maxy AjSij , то есть оптимальное решение задачи (3), (4) равно

T, если A_ks_ik = max AjS_tj _n               .            ⁷ .     , i = 1, n.

0, если A_ks_ik #= max AjS_tj

Тогда условие сбалансированного взаимодействия в системе «заказчик - поставщик» можно записать в виде

(max_k2i_ks_ik - AjS^Xtj = 0,1 = l,n, j = l,m. (5)

С учетом введенных обозначений условие сбалансированного взаимодействия аналитически можно записать как решение следующей задачи:

min

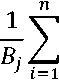
SjjXij -> max при условиях

m max A.k Sik   A.j s ij к                 1 J j=l i = l,n, j = 1, m.

Проведем исследование механизма сбаланси- рованного взаимодействия в предположении что поставщики не учитывают влияния сообщаемых оценок {sij} на вектор цен λ. При этом отметим, что условия равновесия, имеют вид max Akaik - Laij

■ к                      J J i = l,n, j = l,m.          (6)

Сравнивая (5) и (6), легко видеть, что ситуация s* = a является равновесной.

Рассмотрим итерационную процедуру организации сбалансированного взаимодействия в системе «заказчик - поставщик». Для каждого поставщика при любом случае и допустимым s_i существует единственная точка st = f(s) e Vd_bDiA , которую будем называть положением цели i -го поставщика.

Время функционирования системы разбито на периоды с номерами k = 0,1,2,..,. Поведение поставщика состоит в следующем (аксиома индикаторного поведения): каждый поставщик с течением времени изменяет значение собственной переменной в направлении к текущему положению цели s*_i , т.е. движется по направлению к точке s*_i = f_i ( s ). В дискретном случае подобная тактика поведения может быть описана итерационной процедурой

• Vi, к^-, s^¹ = s^ ± /^[sf — s^],

где s^k_i – точка на сегменте [ di, Di ], которую поставщик выбирает в периоде.

Конкретное значение у .^k , определяющее величину шага , может зависеть от времени, текущего состояния и некоторых других факторов, внешних по отношению к модели. Ограничение означает, что в системе отсутствует «перерегулирование», т.е. каждый поставщик делает шаг не больший, чем расстояние (по направлению s_i ) от s_i^k до точки.

Процедуру (7) можно считать адекватной реальному динамическому процессу лишь в предположении, что поставщики делают в нужном направлении заведомо малые шаги.

Если указанное предположение не выполняется, то приходится изучать итерационную процедуру вида

• Vi, k:s^k+1 = s^k + ^sign gt(s^k),

где        означает длину шага

, а                               - функция-индикатор.

Рассмотренные правила поведения заказчика представим в следующем виде:

• 1.                            – стратегия за

• 2.                                 – стратегия

казчика «плюс-минус» шаг;

заказчика «шаг по градиенту»,

{ —1,если gi(s) < 0;

• 0, если yi(s) = 0;

• 1,    если gt(s3 > 0;

• 3.                                       – стра

тегия заказчика «поиск в интервале».

Для обоснования максимальной эффективности сбалансированного взаимодействия в производственной системе рассмотрим задачу оптимального планирования

• c min

  

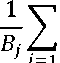
  s^x^ -» max

  
  
  
  

m

m

при условиях j=l j=l 4

. Введем

■ 1 V переменную                 и запишем задачу (8), как задачу линейного программирования

n cy -> max, yBj — ^ atjXtj, = 0, i = l j = l.nV^^Xij = Tbi = l,n.

Выпишем двойственную задачу, определив двойственные переменные

^ Ttvt -» min при условиях v, X > 0,

.

Заметим теперь, что в оптимальном решении двойственной задачи . . Кроме того, ^,j AjBj = С, так как у > 0. Выпишем соотношения дополняющей нежесткости

(vt -Aja^xtj =

i = 1, п, j = 1, т.

ЗАКЛЮЧЕНИЕ

Таким образом, сравнивая (9) с условиями равновесия (6) видим, что они совпадают. Учитывая, что соотношения дополняющей нежест-кости являются необходимыми и достаточными условиями оптимальности решения прямой и двойственной задач. Следовательно, любая ситуация равновесия определяет оптимальный план задачи.