Modeling of heat exchange processes under electrocontact cutting of metals

Electrocontact processing is based on local heating of blank in a place of contact with an electrodetool and also on the removal of the softened or fused metal from a processing zone mechanically: by relative movement of blank or tool.

A distinctive feature of electrocontact processing is the mechanical method of generating impulses by faltering contacting of the rotating disk electrode-tool with a processed detail [1].

The object of research are the processes of heat exchange occurring in a zone of contact of the processed detail and disk electrode-tool which is carrying out cutting with certain speed of rotation and feeding.

For calculation of the process heating and metal cooling during electrocontact cutting it is necessary to choose the suitable settlement scheme allocating the basic features of considered process and neglecting the minor ones. The rational choice of the settlement scheme simplifies calculations and allows revealing the influence of key parameters of the process more exactly.

Depending on the form and the sizes of a product and also from duration of the process of distribution of the heat the scheme of a heated up solid is chosen. On the assumption of conditions of electrocontact cutting process we choose a plate of a small thickness, heat stream in a plate is flat. During the calculations we necessarily consider heat exchange of a plate with environment, however

The cutting zone represents thermal emission and heat sink system. A thermal emission in this zone occurs because of the raised electric resistance of a zone of the contact and a friction between the tool and blank, a heat sink – basically owing to thermal conduction.

2.    Research methodologies

The problem of carried out researches consists in modeling the heat exchange processes under electrocontact cutting of metal by quickly rotating disk, experimental acknowledgement of the results of its decision on mathematical model and an establishment of analytical dependence between electrodetool feeding, modes of cutting (electric parameters) and the heat-physical properties of investigated samples materials.

The decision of a problem of modeling the heat exchange processes is connected with definition of a field of temperatures. In order to establish the dependence between the values characterizing the thermal conductivity phenomenon, we will take advantage of a method of mathematical physics. Now for the decision of the problems of mathematical physics the greatest distribution was received by a method of final elements.

By this method the initial range of functions determination breaks by means of a grid, in our case being irregular, into separate subareas – final elements. As an example on Fig. 1 the final-element grid of mathematical model for the cylindrical aluminum sample is presented.

In Fig. 1 it is visible that the grid has a special condensation in a place of contact of the disk of tool with a processed detail that provides more exact decision of a problem.

Required continuous function is approximated by piece-continuous one, defined on multitude of final elements. Approximation can be set arbitrarily, but more often for these purposes polynomials which are selected so that to provide a continuity of required function in the knots on the borders of elements are used, such calculating method is used in Ansys program.

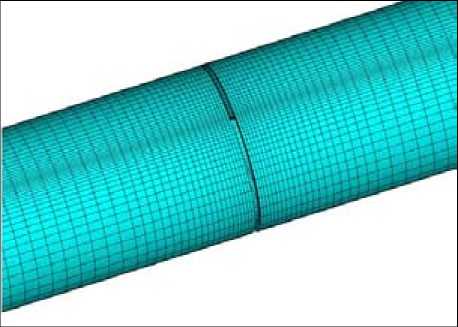
Fig.1. The final-element grid of mathematical model for the examined cylindrical aluminum sample

Modeling of thermal processes under electrocontact cutting was carried out for the following samples: steel rod (steel U8A), an aluminum pipe (D16), a steel pipe (12H18N10T), a copper pipe (M1), a titanic plate (VT1).

By working out of mathematical model it is accepted that temperature distribution by volume of a processed detail is described by the three-dimensional stationary equation of the heat conductivity, presented as:

div ( A T ) grad ^- >0,                                               (1)

where λ – Factor of heat conductivity, Vt/(m∙K); Т – temperature, K.

The thermo physical properties of a processed samples material were used as function from temperature. On external surfaces the boundary conditions of the third sort have been set:

- A d T = a , ( T - T oe ) ,                                                     (2)

о n where Т – Metal temperature, K; Тос – outside temperature, K; а∑ – total heat emission factor, Vt mvK).

On the face surfaces the boundary conditions of the second sort have been set:

A -- = 0. n

In a zone of the contact of the electrode-tool (disk) with processed blank the thermal stream defined in electric parameters (modes) of cutting has been set.

The system of the nonlinear algebraic equations (4) in our problem was solved by means of Newton-Rawson’s iterative method [2]. The defined value is the temperature for which polynomials are worked out.

a 11 t + a 12 t +..+ a 1_n t = 0

a 21 t + a 22 t +..+ a 2_n t = 0

a 31 t + a 32 t +..+ a 3n t = 0

a n1 t + a n2 t +..+ a nn t = 0

Nonlinearity of the equations is explained by the dependence of heat conduction of material on the temperature. The problem decision was conducted by a method of final elements by means of Ansys program.

3.    Interpretation and discussion of research results

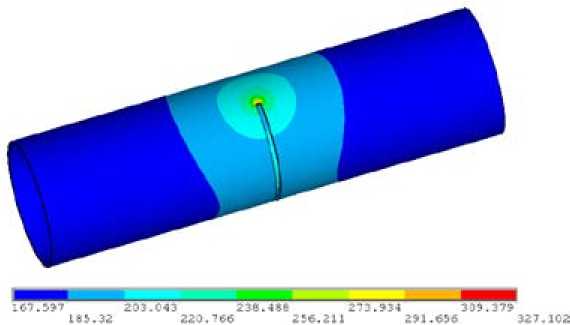
As an example calculated temperature fields of the aluminum sample (pipe), steel (rod) and the titanic sample (plate) are showed in Fig. 2-4.

The calculation of temperature fields was carried out at different modes of cutting been set on the basis of the skilled data. The analysis of the received results shows that cutting of metal can be carried out as at the temperature of the fusion in a zone of contact of a cutting disk and blank, as at the temperature of recrystallization.

The temperature of recrystallization is determined by following expression [3]:

07. W      207.043

185.32         220

Fig. 2. Distribution of temperature fields in an aluminum pipe

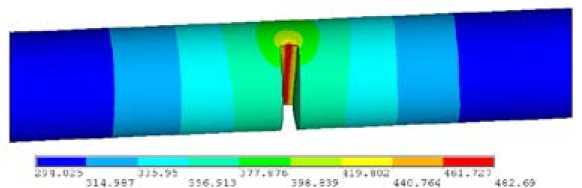
Fig. 3. Distribution of temperature fields in steel rod

>71. ?и

vn.w

Fig. 4. Distribution of temperature fields in a titanic plate

T r = 0,5 4- 0,6 T ,                                                                        (5)

where T r – Recrystallization temperature of metal; T – Temperature of fusion of metal.

The cutting under the temperature of recrystallization will allow to lower specific power inputs considerably and also improve technological indicators of the process. For maintenance of the given temperature in a zone of contact of the electrode-tool and a processed detail it is necessary to observe appropriate modes of cutting: pressure, a current strength and electrode-tool feeding.

Approbation of mathematical model was made by comparison of the received results with the data of experiences.

The following samples have been subjected to electrocontact cutting: steel rod (steel U8A), an aluminum pipe (D16), a steel pipe (12H18N10T) and a copper pipe (M1), a titanic plate (VT1).

The geometry of samples is presented in Table 1.

The comparison shows the correct character of temperature distribution as far as metallographic analysis of examined samples confirms that the temperature in a zone of contact of electrode-tool with processed detail corresponds to the temperature of recrystallization.

The microstructure of the steel sample from a steel of mark U8A (Fig. 5, a) is homogeneous, there is not differentiation on zones, there is no dendritic structure. Thus in the cutting process melting did not occur.

Microstructural analysis of the aluminum sample (Fig. 5, b) shows that cutting of pipe from an aluminum alloy leads to exfoliating the top layer. Metal parts are as though stick to a surface, forming rough “crust”. During cutting process melting has not occurred.

Deeper metallographic structure research has shown that in cross-section of a pipe 3 zones are observed. The first (is closer to edge) and the third (central) zones are fine-grained, forming dispersed

Fig. 5. Microstructure of examined samples: a) steel U8A; b) aluminum D16; c) titan VT1

Table 1. Geometrical parameters of research samples

Material	Diameter, mm		Thickness, mm
	D external	D internal
Aluminum (pipe)	40,88	38,60	2,28
Steel 12H18N10T (pipe)	16,1	13,5	1,3
Copper М1 (pipe)	8,45	6,55	1,9
Steel U8A (rod)	12,5		–
Titanium VT1 (plate)	20,5		1,6

Fig. 6. Microstructure of examined samples: a) copper М1; b) steel 12H18N10T

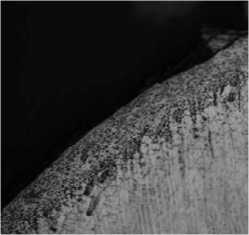
“crust” on a surface by means of heat sink deep into the metal and in an environment (air). It leads to the accelerated cooling and, as consequence, to the reception of fine-grained structure. Such distribution of structure is connected with a temperature gradient on pipe section, irrespective of a current strength given at cutting process. Also the presence of these zones is observed at the studying of a longitudinal section of a pipe, i.e. in a zone of contact with the cutting tool.

Metallographic analysis of the sample of mark VT1 (Fig. 5, c) shows that a zone of thermal influence is very narrow, melting has not occurred. At an edge the structure is granular, grains have the accurate geometrical form, to the centre there is a grain integration.

During metallographic research of copper samples it is visible that by means of heat conductivity the growth of grains occurs faster and the depth of the changed layers is larger than at aluminum samples. In drawing 6а, superficial separations of the softened layer are shown. Metal slices are as though pasted to a pipe surface. They did not form solidness and have empty spaces.

The analysis of structure of the steel sample in cross-section shows columnar crystals of solid solution on external edge, further structure form looks like honeycombs (Fig. 6).

It speaks about melting at cutting process even at rather small working current (Ip=35÷45A). At reduction of a current strength and electrode-tool feeding it is sharp samples from a steel 12H18N10T passes at the temperature of recrystallization.

4.    Summary and Conclusions

• 1.    The choice of the settlement scheme was made truly that was confirmed by distribution of temperature fields by a thickness of examined samples.

• 2.    The coincidence of theoretical preconditions with practical results testifies to adequacy of the chosen model.

• 3.    The developed way of electrocontact cutting of metal allows to lower specific power inputs at metal processing and to simplify the realization of a method by feeding of the electrode-tool with the speed depending on the temperature of recrystallization, on heat-physical properties of metal and on the thickness of processed blank [4].

• 4.    Metallographic analysis of examined samples confirms the results of modeling of electrocontact cutting process and the possibility of influence on technological indicators of process.