Modeling Prioritized Hard Handoff Management Scheme for Wireless Mobile Networks

Published Online August 2012 in MECS DOI: 10.5815/ijcnis.2012.08.03

At the present time, traffics(requests and demands for mobile communication facilities) in the upcoming wireless mobile networks (WMNs) are expected to be extremely non stationary [1]. The channel associated with the current connection serviced by a base station (BS) is changed while a call is in progress. Continuous service is achieved by supporting handoff [2] from one cell to the next adjacent cell as the mobile station (MS) moves through the coverage area. The handoff alg orithms are able to determine the dynamics of the MSs which move through theWMNs [3][4].

Several competent factors influence to occur a handoff . Two of them has more significant effect on it. One, when a MS moves across a cell boundary from the servicing BS to another BS . Second, deterioration in quality of the signal in the current channel [2][5][6]. The handoff phenomena in WMNs and mobile cellular communications environment have become progressively more important issue as cell sizes shrink to accommodate an increasingly large MSs in terms of demand for services ( traffics ) [7]. In this paper, we present a novel lookup on a priority handoff . scheme in a channelized cellular system and WMNs . The term handoff in this paper refers a hard handoff . Another type of handoff is the soft handoff [2]. How a hard handoff is ensured to MSs in WMNs is shown in Figure 1.

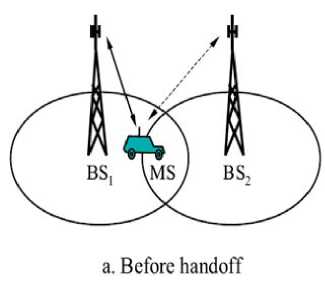
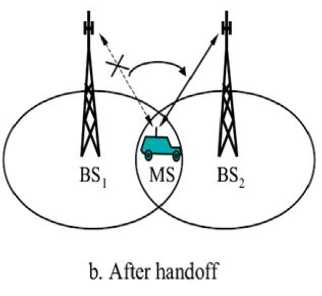
Figure 1. Hard handoff between the MS and BSs.

The Figure 1 shows two cases of the current situations of a MS – before and after handoffs . In Figure 1. a we see that a MS is serviced by BS and it is moving towards BS without any handoff taken place. In the Figure 1. b we see that a MS has entered in a handoff region. Its services by BS are cut off and are gained by BS . Eventually a handoff is thus just occurred.

In hard handoff the MS is thus handed off from its current BS to possible nearest BS . At the moment the MSs leave a cell of a the coverage area of the BS and enters into a new cell of the coverage area of the BS . In this case, the active set of MSs therefore consists of at most and only one BS at any given time [3].

The decision on the handoff to be taken place from one cell to the other is based on various criteria that take into account of channel degradation considerations too

• [5] . However, the initial (and most important) trigger for

underlying BS . This BS is also known as mobile ter min al (MT) [8][9]. The S BPQ model [8] has taken into account the performance of handoff behavior on the basis of received or relative signal strength (RSS) [5][6][10][11]. The simulated results suggest that a handoff   point  (the maximum allowable radial distance   from   BS at which

MSs possibly gets serviced by another nearest BS instead of its current servicing BS ) for a MS depends on various parameters that have direct impact on this RSS as determined by Equation (1) in [8][10]. Suppose the radial distance of MSs from aBS (MT) is r . Calls are generally two types – originating calls , and handoff calls . In this paper we suggest a simulation model MH S with  priority handoff scheme for modeling and implementing a traffic mod el , and evaluating blocking probabilities of originating calls (B ) , and handoff calls (B ) with the selected traffic mod el [2][8]. All these are performed once we have completed the computation of arrival rate of hando calls (λ ) of the traffic mod el selected in this paper.

The cellular structure which is considered in all the cases such as S BPQ [8], EATM [13], and MH S models is shown in Figure 2. This is a well known and well efficient cellular classification of the coverage of a MT and is used in practice. The Figure 2 shows a part of the total cellular configuration (coverage area of a servicing BS ). It is actually a segment taken at 120o orientation of the area.

a handoff is generally based on pilot signal

strength measurements taken for a MS at the

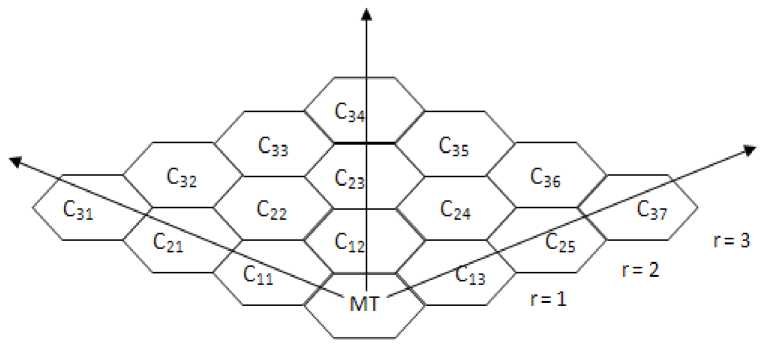
Figure 2. A typical cellular configuration of underlying MT for r = 3.

We organized our paper as follows. First, we start with some preliminary assumptions which have been assumed in Section II. Second, the proposed work has been elucidated in section III. In this section we have selected a traffic mod el followed by modeling it. The model is best suitable for the assumptions would be taken in preceding Section.. We are here able to derive some suitable mathematical expressions for several attributes of the selected traffic mod el . Third, performance of the proposed model MH S is appraised with simulation in Section IV. The simulation has been shown both in numerical and corresponding graphical. The paper is over and completed drawing some remarkable conclusions. This has been given in Section V.

• II.    Preliminaries

We have already known that the RSS measurement is one of the most common criteria to initiate a handoff [5][6]. We assumed two base stations mod el in [3][8][11][12] as primary objective of a handoff a lg orithm that provides a good signal quality. We consider only that portion of the trajectory on which the signals received from the two BSs are the strongest. Generally, a high RSS means good signal quality, so the handoff to another BS cannot be occurred unnecessary, because the MS is being served well by the current servicing BS and on a handoff taken place, all the services must be quit from the current BS . We restrict our analysis to short radial distance r horizons over which a MS moves from one radial distance to another with fixed velocity in any direction (away from current BS , towards BS , or along same radial level from current BS ) with equal probability of movement. Movements of MSs in cells are shown in Figure 3 [14] . However, movements of the MSs are unrestricted and random in nature.

Figure 3. Movements of the MSs.

Although the MSs move randomly in the coverage area. But a handoff is only possible as already we know when a MS either crosses a cell boundary merely or its RSS is lower than threshold value. Crossing a cell boundary may be possible three ways. First, when MSs move from a cell in radial distance r to a cell at radial distance ( r + 1) . Second, this case is exactly opposite to the previous one. That means MSs in this case move from a cell in radial distance r to a cell at radial distance ( r — 1) . Third, MSs in this case move from a cell to another along the same radial distance r . However, third case is very less responsible for a handoff to be happened since RSS of the underlying MTs for MSs remains same. Second case is also less responsible for a handoff to be happened since RSS of the underlying MTs for MSs become strengthen since the MSs in this case move towards their servicing MT . The three cases of movements of the MSs have shown graphically. The Figure 4 represents them. Here any node numbered as ij , i , j G N in Figure 4 represents any cell C of the cellular structure shown in Figure 2.

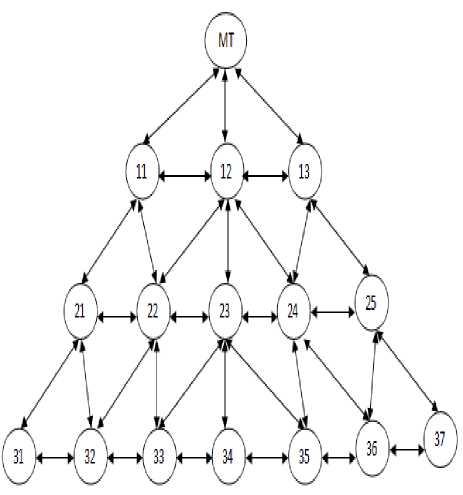
Figure 4. Graphical presentation of movements of MSs.

The MSs also called mobile callers ( MCs ) are evenly distributed over the coverage area of a BS as shown in Figure 3. That means a basic system model assumes that the new call origination rate is uniformly distributed over the mobile service area [2][3][4][5][8][9][10][11][15][16][17]. But it is seen that MSs arrive in a BS randomly. This means requests of MSs are made non-uniformly. We assume these requests are made according to Poison distributions [18].

• III.    Proposed Work

In next-generation wireless systems and WMNs it is important for the MSs to ensure that the system is guaranteeing their needed requirements. These basic requirements would improve the quality of service ( QoS ) provided by WMNs . Therefore, a proper traffic management scheme is required to effectively manage the ever increasing traffics ( MSs ) which are non stationary at and is on the way away from the servicing BS in the system. There are many proposals to solve the dilemma [1][19]. Our approach provides high precise location and tracking of MSs by exploiting advanced traffic mod els . Some of these we have studied in [7][8][15][20]. Here we have extended our previous work [8][13] with El - Dolil et al .' s traffic mod el [2]. Our proposed model MH S takes more advantages over previous model described in [7][8][13][15].

The major functionalities of the proposed model MH S have been classified into following sub areas. First,   we   determine arrival rate (λ ) of originating calls . Second, we determine depurture rate (µ) of MSs that gets serviced by their servicing BS . Third, we select a suitable traffic mod el for implementation. Four, we have chosen a scheme for handoff based on priority. Five, we allocate some channels to originating calls , handoff calls , and handoff requests . Last, more influencing factor of the model call blocking rate (CBR) is determined.

• A.    Determination of λ

Number of MSs ( traffic density [18]) varies location to location. And this location on the contrary affects arrival rate λ o  of originating calls from

MSs to their underlying BS . Likewise number of BSs are also varied. Assuming distance D [4][17] between nearby two BSs is 1-3 km, λ o has been determined here similar to S BPQ model [2] [8] as:

Total Subscribers ( S ) in the Re gion λ o ≈                                            (1)

Total Number of MTs ( X )

• B.    Determination of µ

The model S BPQ [8] might be competent of providing services to all (may be infinite number) MSs with no or least waiting time after initiating a call

(request for service). Thus, departure rate µ

(number of MSs get serviced in unit time) should be at least equal to λo such that waiting time for getting services generally becomes zero or very less. Exploiting

Poison distributions [18], and the traffic intensity factor ρ defined as

λ

µ

lies in the range[0 - 1] , departure rate µ has been considered similar to

S BPQ and EATM models [8][13] as:

0≤ρ≤1Ф    0 < ^о/ < 1

µ

^ 0<ХО<ц

However, µ should be much greater than λ so that the MSs get services on their request immediately. Waiting calls are enqueed in a busy list. A call in this list does exist for a little time quanta. When a time quanta is over and the call is not scheduled for services, it is then dropped from the list.

• C.    Selection of Traffic Model

Every cell in cellular network architecture is served by a BS . The BSs are connected together by using a wireless network . Establishment of a traffic mod el , in cellular system, is more imperative before analyzing the performance of the system [7][8]. Several traffic mod els [2] have been established on basis of making different assumptions about user mobility. We measure the performance of handoff a lg orithms in terms of the exp ected rate of handoff ( λ ) .

This is one of the parameters used to analyze handoff performance[5][9]. We consider El - Dolil et al.'s traffic mod el [2] which is shown in Equation (5).     The selected traffic mod el is represented in terms of performance parameter i.e. the arrival rate of handoff calls (λ ) . The λ is then given by:

λ H = ( R cj + R sh ) P hi + R sh P hh                  (5)

Where,

R = average rate of total calls carried in cell j .

R = the rate of successful handoffs .

P = the probability that a mobile station needs a handoff in cell i .

P = probability that a call that has already been handed off successfully would require another handoff .

The model has been chosen as underlying implementation model based on some basic assumptions. One, the highway is segmented into cellular structures (microcells) with small BSs . Second, along the highway mobile radio signals that are radiating are cigar-shaped [2][8]. We have derived general mathematical expressions for these parameters of the Equation (5) as follows.

• 1)    d etermination of R : Consider Figure 2 again. At radial distance r = 1 from servicing BS ( MT ) , number of cells is 3. In the same fashion at r = 2, 3… R

number of cells are 5, 7... (2 x R_{m x} + 1) respectively.

Thus, R represents maximum radial distance or handoff po int [8]. In general, total cells N under the coverage area of a typical BS is given by:

R max

N = £ (2 r + 1)                          (6)

r = 1

However traffic density is not uniform. For better services, a BS should have some number of MSs to make it busy and the BS should not be overloaded some time. Although this not the actual cases. Because a BS may be overloaded some time or may goes down with performances. Average number of MSs , Subs in any cell j at any r from its BS (represented as C ) is obtained as:

Total Number of MSs ( S )

Subs =------------------—        (7)

Total Number of Cells ( N )

The Subs are not actually MSs rather they are meant by the MSs who have already made requests. The MSs are allowed making any number of requests.

Let us assume a term that an average number of calls (requests) originated by subscriber ( MS ) is calls per day per subscriber ( CPD ) . Thus

R can be determined at any particular radial distance j from the current BS as:

R cj = П ( Subs , CPD,(2 j + 1)), j = 1,2... R mx (8)

• 2)    d etermination of R : The MSs are non stationary. When a MS is moving away from its BS , its RSS value is decreasing. Therefore, a MS has a chance to be handed off and probably is handed off from serving BS to another BS when this RSS value gets decreased below at least 50% of its original strength value [8]. The RSS is sampled at discrete time instants t j = kt_s , where t_s is sampling time and corresponding sampling interval in distance is d s = Vt . . Here, V is constant velocity of a MS [12]. Thus, at the radial distance      from the current BS , a

,                                  max handoff for the MS occurs first time. However, before a call (MS) is handed over from BS to another BS it has to travel a radial level.

Therefore, Subs are gradually increased when MSs move to r from ( r + 1) .

We assume for simplicity that two-third movement of the MSs take place to immediate upper radial level from current radial level. Few of them may come back to their starting radial distance. Therefore total number of MSs moved away from their BS are effectively less, We assume that one-third of the MSs move back to its immediate lower radial level from current radial level. These movements are applicable to all the radial level. Thus, taking effect of both in — just upper and lower radial levels, R at any level r from its nearest BS has been determined in Equation (9) as:

R

sh

(( 2           1

П I T⁽2 ^{r +} 1 ) ⁺7 (^{2 j +} 1H S^ubs , ^r = 1, ^j = ^{r + 1}

VV 3          3       ))

П к(2i +1)+ 7(2r +1)+ 7(2k +1) I-Subs , r = 2, 3

VV3         3          3       ))

i = r — 1, k = r

• 3)    d etermination of P : Movements of the MSs are either towards or away from current serving BS and are primarily responsible for handoff mechanism to be taken place. Every MS has same opportunity to be handed over . Let us choose any mobile station MS at any radial distance r , 1 <  r <  R ^ from its underlying BS . Therefore, the probability of selection of MS could be represented as:

  P ( MS ) =

  
  

  2 r + 1 + 5

  
  
  
  

Where 5 = a constant factor assumed as the effect of adjacent cells (left and right most) at any r .

We consider the value of 5 equals to 2 when a MS moves towards BS and 0 when it moves towards BS .

The P(MS ) can be computed in two ways. One, in — ward handoff probability Ph (Ф) in a cell i. Second, out — ward handoff probability Ph (T) in a cell i . These names are given according to the movements of MSs. The P (Ф)  is likely to be happened when MSs move towards their servicing BS . And, the Ph (T) is likely to be happened when the MSs move away from their servicing BS . Here, bothPh M, and    Ph(T)are int er — level handoff probabilities . However, an actual handoff for a MS takes place at r = R^ . Another interesting thing is

that the probability P (Ф) decreases the chances of handoff to be occurred till r > 1 while the probability  Ph (T) enhances the chances of handoff to be occurred till r < Rm. Assuming initial values of Ph (Ф), and Ph (T)are zero, We compute them as:

P (ф) = 1 у I P  (ф) + -J— I, i = R 2,1 (11)

h                   hmax

'         3 , V ' ^{+ 1}         2' + 3 )

And,

Ph (T) =1УI P (T) + — |,i = 1,2...R(12)

h                    hmax

Now, a handoff point (the maximum radial distance of a MS from its servicing BS ) is at r < R-^ . Before reaching a MS to a handoff po int it may have either P (Ф) or P (T). Therefore, at any level r, 1 < r < R, the probability P that a MS needs a handoff in cell i can thus be urged as below.

Ph' = 1 — (Ph'(T) + Ph (Ф)) r = 1,2.... R_ (13)

• 4)    d etermination of P : We have exploited the property that two-third of the MSs at radial level r move to immediate upper level ( r + 1) and one-third of the MSs at radial level r move to immediate lower level ( r — 1) . Some of the MSs under BS. at the handof po int may move to ( R ^ +1) which is similar to R from BS . Second handoff may occur when MSs eventually come back to R with respect to BS . Therefore, the probability of next handoff P of a MS may be determined as –

  R max

  
  

  p =

  ¹ hh

  
  

1 f 2 Rmax 1 --> — +

3V3£13r

1 I

O R max

3   )

r = 1

• D.    Priority Handoff Scheme

A handoff request is generated in a cell when a MS approaches the cell from a neighboring cell with significant signal strength. Priority is set to handoff requests and their types. Some channels are necessarily assigned in a cell. These assigned channels may be exclusive or shared. Suppose, S channels have been assigned exclusively for handoff calls out of S channels . And, both originating calls and handoff requests share the remaining S_c = S — S_R channels. An originating call call is blocked if the number of available channels in the cell is less than or equal to S . Similarly a handoff request is blocked if no channel is available in the target cell. The system model for the channels sharing is shown in Figure 5 [2][7].

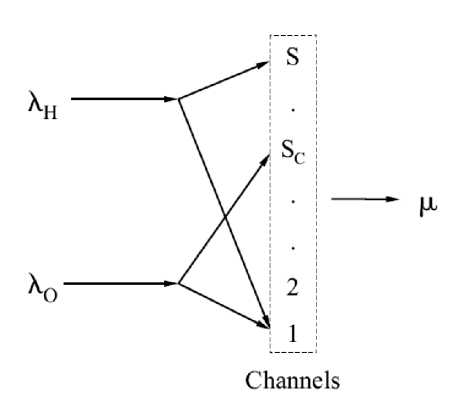
Figure 5. System model with priority for handoff call.

Two important parameters can be derived from this allocation of channels. These are blocking probabilities B of originating calls , and B of handoff requests [2][7][8] respectively. They have been determined by Equations (15), and (16) with the steady-state probability P ( i ) [2] respectively.

S

B o = 2 P ( i )                            (15)

i = S_c

And,

_ (Л + Л н ) S C Л S C

BH =-----S-^S-----P(0)

Here P (0) [2][7] states steady state probability when the system is in state "0" . We define the state i , i = 0,1,2...... S of a cell as the number of calls in progress for the BS of that cell.

• E.    Channel Allocation Scheme

A new call holds the channel until the call is completed in the cell or it move out of the cell. A successful handoff call holds the channel until the call is completed in that cell. Thus, handoff call is admitted until all channels are busy [21]. In the evaluation of handover (handoff) performance, number of channels to be allocated for handoff requests , and originating calls are exclusively important very much along with other factors such as RSS , R etc [2][22]. Already we have seen that how some channels S are necessarily assigned in a cell for handoff calls , handoff requests , and originating calls . Although all the channel allocation schemes are facing the same challenge that how the channels could be distributed (allocated) effectively to these calls. Because the amount of channels in terms of frequency ranges is fixed.

• F.    Determination of Call Blocking Rate

A MS when initiates a call, it generally expects to be get serviced immediately. Types of requests are different. Before a request gets serviced, it must be enqueed in priority queue[8][23]. Afterward a call gets serviced by its current MT (BS ) taking advantage of Splay operations on the Splay Tree [24] implementation of the priority queue generated in [8]. The selection of a call in the Splay Tree , follows SIRO queuing principle [18]. So, more and more number of cells are getting services in a cell. At particular radial level r , r = 1, 2....R and a specific time instant, number of max calls blocked (enqueed) for availing services i.e. call blocking rate (CBR ) [25] could be decided as:

CBR r = 1 H R». , B o , ( 2 r + 1 ) )         (17)

We will show that this CBR_r , r = 1, 2.... R ^ will be increasing with r increases.

• IV.    Simulation Work

  The parameters used for simulation are commonly used to analyze handoff performances . We simulated our model MH S in MATLAB Version 7.6.0.324 (R2008A). Numerical values of the fundamental parameters for handover initiations , Л , and R are based on COAI REPORT [26][27] developed for beloved Megacity Kolkata. These parameters are set as Л = 1991, and R = 2212 [8]. Exploiting these numerical on all the Equations (5) through (17) whenever necessary are assessed. Here we have shown two observations. We assume that the shadow fading effect ζ (r) is log(r) in all the observations.

Observation I: Let us suppose that a MC makes at least 5 requests per day ( CPD ) . We assumed Є = 0, and η = 20 in Equation (1) [8] and we found R = 14. Using Equation (6) and Equation (7), total number of cells N and average number of MSs in any cell Subs are found 224 and 2.9632 respectively. Other values are shown in Table I.

Table I: Simulation of MH S for CPD = 5.

Parameters	Numerical Outcomes Under Current Base Station Level Wise
Rcj	44.44742    74.07904    103.7107 133.3423    162.9739    192.6055 222.2371    251.8687   281.5004 311.132    340.7636   370.3952 400.0268    429.6584
Rsh	10.86493    19.75441    27.65617 35.55794    43.4597    51.36147 59.26323     67.165     75.06676 82.96852    90.87029   98.77205 106.6738    114.5756
Phi	0.80067     0.83163     0.86666 0.89321     0.91206     0.92555 0.93549     0.94306     0.94903 0.95388     0.95797     0.96166 0.96559     0.97131
Phh	0.11111
λ H	28.09555    47.37267   68.98609 91.29296    113.8331    136.4347 159.0444    181.6503    204.2531 226.8593    249.4859   272.1833 295.1101    318.7731
λ O	22.8851
µ	25.4278
B O	0.75684
BH	0.089776    0.12517     0.17025 0.21778     0.26604     0.31441 0.36272     0.41096     0.45914 0.50731     0.55555     0.60407 0.65355     0.70618
CBRr	33.639646   93.44346   183.14918 302.75681   452.26635  631.67779 840.99114   1080.2064   1349.3236 1648.3426   1977.2636  2336.0865 2724.8113   3143.438

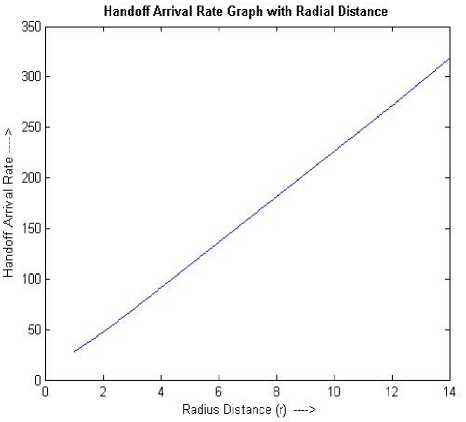
Figure 6. Arrival rate of handoff requests.

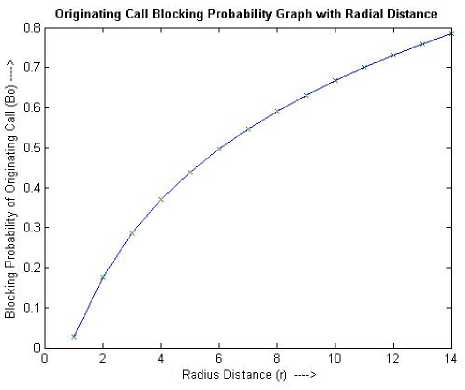
Figure 7. Growth of BO for originating calls.

The graphical representations of the parameters λ _H , B_O , B_H , and CBR_r produced in Table I for Observation I , have been shown in the Figures 6 though 9 respectively.

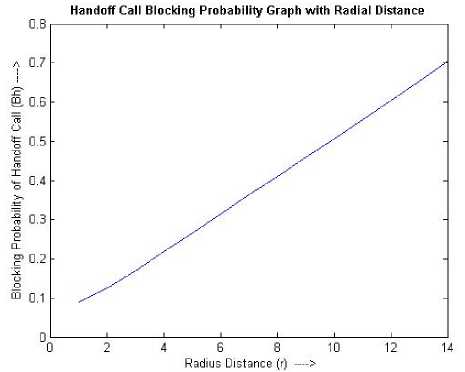
Figure 8. Growth of BH for handoff calls.

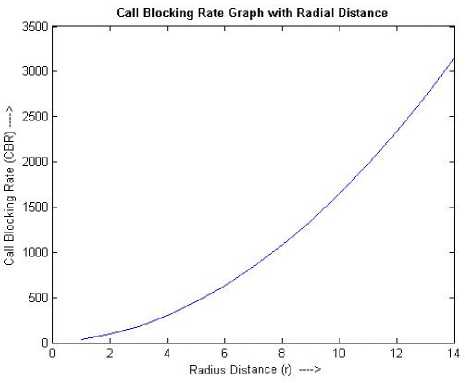
Figure 9. Growth of call blocking rate.

Observation II: Let us suppose that a MC makes at least 6 requests per day ( CPD ) . In the same way (simulation made in Observation I) assuming Є = 0, and η = 21 in Equation (1) [8], we get R = 12 . Similarly N and Subs are obtained as 168 and 3.9509 respectively from Equation (6) and Equation (7) respectively. Other values are shown in Table II.

Similarly, the graphical representations of the parameters λ , B , B , and CBR produced in Table II for this Observation II , have been shown in the Figures 10 though 13 respectively. First we showed Figure 10 which represents the parameter λ . Other Figures 11 through 13 have been shown after Table II.

The CPD values are increased in both the observations by 1. Other higher values could be assigned to CPD . However, in general it is seen that CPD values are not changed suddenly. These values are based on the statistics collected from certain percentage of general people.

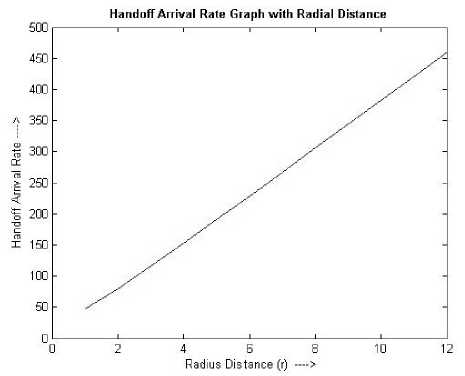
Figure 10. Arrival Rate of handoff requests.

Table II: Simulation of MH S for CPD = 6.

Parameters	Numerical Outcomes Under Current Base Station
Rcj	71.11588    118.5265    165.937 213.3476   260.7582    308.1688 355.5794     402.99     450.4006 497.8111    545.2217    592.6323
Rsh	14.48657   26.33921    36.8749 47.41059    57.94627    68.48196 79.01764    89.55333    100.089 110.6247    121.1604    131.6961
Phi	0.80067     0.83163     0.86666 0.89321     0.91206     0.92555 0.93551     0.94313     0.94922 0.95444     0.95964     0.96668
Phh	0.11111
λ H	46.95075    79.59185    115.9499 153.4849    191.4158    229.4519 267.5049    305.5608    343.6436 381.8374   420.4091    460.2128
λ O	26.5467
µ	29.4963
B O	0.032694    0.19616     0.31293 0.40374     0.47805     0.54092 0.59541     0.64349     0.68651 0.72543     0.76097     0.79366
BH	0.12074     0.17735     0.24776 0.32228     0.39813     0.47429 0.55046     0.6266     0.70281 0.77945     0.85757     0.94058
CBRr	58.126376   161.46216  316.46583 523.13739  781.47684   1091.4842 1453.1594   1866.5025  2331.5135 2848.1924  3416.5392  4036.5539

Blocking Probability of Originating Call (Bo) -

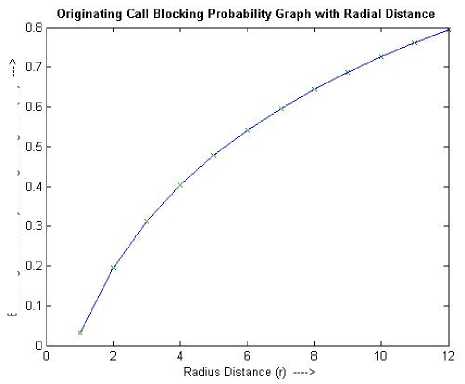
Figure 11. Growth of BO for originating calls.

when the MSs are mobile. We are able to present an easy method that evaluates priority scheme on selection of a suitable traffic mod el analytically. Simulation results show that our algorithm performs better than some existing handoff alg orithms . The proposed model MH S can achieve satisfactory number of handoffstaken place on an average. Compared with other handoff alg orithms , the only overhead of the proposed algorithm is proper allocation of channels. Therefore,     our     algorithm     can     improve handoff performance effectively at the cost of very marginal overhead comparatively with less number of channels. It is observed that increasing average number of calls per MSs per day i.e. CPD helps to improve the B  for both handoff requests , and originating

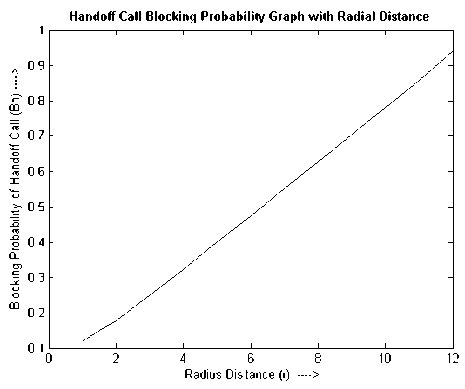
Figure 12. Growth of BH for handoff calls.

calls . And these values are nearer to their actual values. Another achievement of the proposed model is working out of rate of blocked calls ( CBR ) in addition.

• VI. Acknowledgements

  

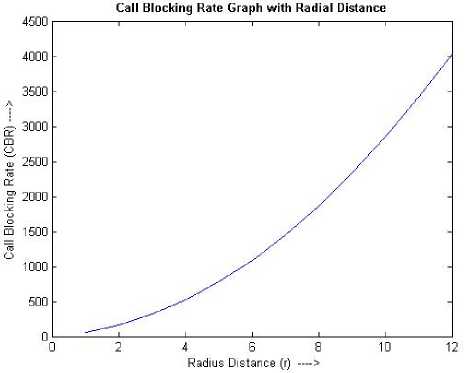
  Figure 13. Growth of call blocking rate.

  
  

• [1]    N. Mohan, T. Ravichandran, “An Efficient Multiclass Call Admission Control and Adaptive Scheduling for WCDMA Wireless Network”, European Journal of Scientific Research, Vol. 33 No. 4, 2009, Pp.718-727.

• [2]    Ivan Stojmenovic, Qing-an Zeng and Dharma P. Agrawal, Handbook of Wireless Networks and Mobile Computing , John Wiley & Sons, Chapter 1, 2002.

  V. Conclusions

  To the best of our knowledge, it is the first time that an explicit mathematical derivations have been proposed to calculate arrival rate of handoff calls λ

  
  

• [3]    Alexe E. Leu , Brian L. Mark , “ A Discrete-Time Approach to Analyze Hard Handoff Performance in Cellular Networks”, IEEE Transactions on Wireless Communications, Vol. 3, No. 5, 2004, Pp: 1721 – 1733.

• [4]    S. A. Mawjoud, “Simulation of Handoff Techniques in Mobile Cellular Networks”, Al-Rafidain Engineering ,Vol. 15 No.4, 2007, Pp: 31 – 39.

• [5]    Huamin Zhu and Kyung Sup Kwak, “An Adaptive Hard Handoff Algorithm for Mobile Cellular Communication Systems”, ETRI Journal, Volume 28, Number 5, October 2006, Pp: 676 – 679.

• [6]    Sanjay Dhar Roy, “A Timer based Handoff Algorithm for Multi-cellular Systems”, ICETET 2008, IEEE, Pp: 819 – 822.

• [7]    Biswajit Bhowmik, Smita Roy, Parag Kumar Guha Thakurta, Arnab Sarkar, “Priority Based Hard Handoff Management Scheme for Minimizing Congestion Control in Single Traffic Wireless Mobile Networks”, International Journal of Advancements in Technology, Vol. 2(1), 2011, Pp: 90-99.

• [8]    Biswajit Bhowmik, Pooja, Piyali Sarkar, Nupur Thakur, “Received Signal Strength Based Effective Call Scheduling in Wireless Mobile Network”, International Journal of Advancements in Technology, Vol. 2(2), 2011, Pp: 292 – 305.

• [9]    Rajat Prakash, Venugopal V. Veeravalli, “Adaptive Hard Handoff Algorithms”, Proc. VTC’99, Houston, TX, May 99.

• [10]    Mohmmad Anas, Francesco D. Calabrese, Preben E. Mogensen, Claudio Rosa, Klaus I. Pedersen, “Performance Evaluation of Received Signal Strength Based Hard Handover for UTRAN LTE”, IEEE Vehicular Technology Conference, April 2007, Pp:1046 – 1050.

• [11]    Venugopal V. Veeravalli, Owen E. Kelly, “A Locally optimal handoff algorithm for cellular communications”, IEEE Trans. on Vehicular Technology, 1997, Pp: 1 – 8.

• [12]    Sanjay Dhar Roy, “Performance Analysis of Handoff Algorithms for Multihop Ad Hoc Wireless Network”, ICETET 2008, IEEE, Pp: 157 – 161.

• [13]    Biswajit Bhowmik, Pooja, Nupur Thakur, Piyali Sarkar, “Experimental Analysis of Xie and Kuek’s Traffic Model with Handoff Scheme in Wireless Networks”, Int. J. of Information Engineering and Electronic Business , Vol. 4, No. 1, 2012, Pp: 34-43.

• [14]    Hua Jiang and Stephen S. Rappaport, “Hand-Off Analysis for CBWL Schemes in Cellular Communications”, CEAS Technical Report, No. 683, 1993.

• [15]    Biswajit Bhowmik, Arnab Sarkar, Parag Kumar Guha Thakurta, “Simulation of Handoff Management Scheme for Improved Priority Based Call Scheduling with a Single Traffic System in Mobile Network”, Int. J. of Advanced Research in Computer Science”, Vol. 1(3), 2010, Pp: 354-358.

• [16]    Biswajit Bhowmik, Design and Analysis of Algorithms , S.K. Kataria & Sons, Second Edition, 2012.

• [17]    Raymond M. Bendett and Perambur S. Neelakanta, “Alternative Metrics for Hard Handoffs in Mobile Communication”, ICPWC 2000, IEEE, 2000, Pp: 43 – 46.

• [18]    J K Sharma, Operations Research - Theory and Application , Macmillan Publishers, 3/e, 2006.

• [19]    Azita Laily Yusof, Mahamod Ismail, Norbahiah Misran, “Traffic Management Algorithm and Adaptive Handover Initiation Time for Dynamic Traffic Load Distribution”, IJCSNS International Journal of Computer Science and Network Security, Vol 8 No7, 2008, Pp: 203 – 207.

• [20]    Marco Anisetti, Claudio A. Ardagna, Valerio Bellandi Ernesto Damiani, Salvatore Reale, “Advanced Localization of Mobile Terminal in Cellular Network”, I. J. Communications, Network and System Sciences, Vol 1, 2008, Pp: 95 – 103.

• [21]    Nguyen Cao Phuong, Sang-Ho Lee, Jung-Mo Moon, Tran Hong Quan, “Priority-based Call Admission Control of multiclasses in Mobile networks”, ICA0T2006, IEEE Xplore, Feb. 20-22, 2006,Pp: 1471 – 1474.

• [22]    Hsin-Piao Lin, Rong-Terng Juang, and Ding-Bing Lin, “Improved Location-Based Handover Algorithm for Mobile Cellular Systems with Verification of GSM Measurements Data”, IEEE Trans. on Vehicular Technology, 2002, Pp: 5170 – 5174.

• [23]    Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein, “ Introduction to Algorithms , PHI, 2nd Edition, 2006.

• [24]    D. Samanta, Classic Data Structures , PHI, 2nd Edition, 18^th printing, 2010.

• [25]    P. K. Guha Thakurta, Souvik Sonar, Biswajit Bhowmik, Swapan Bhattacharya, Subhansu Bandyopadhyay, “A New Approach on Priority Queue based Scheduling with Handoff Management for Mobile Networks”, 19^th Int. Conf. on SEDE, ISCA, 2010, Pp: 69 – 74.

• [26 ]    http://www.coai.com/study_papers.php?val=2010

• [27 ]    http://en.wikipedia.org/wiki/Kolkata#Geography.