Modeling the effect of network access control and sensor random distribution on worm propagation
Автор: ChukwuNonso H. Nwokoye, Njideka Mbeledogu, Ikechukwu I. Umeh, Ihekeremma A. Ejimofor
Журнал: International Journal of Modern Education and Computer Science @ijmecs
Статья в выпуске: 11 vol.9, 2017 года.
Бесплатный доступ
Sensor networks are appealing targets for malicious attacks that invade the network with the aim of depleting the confidentiality, availability and integrity (CIA) features/parameters of neighboring sensor nodes. This is due to its open communication, minimal resources and its deployment in un-trusted, unguarded and unfriendly terrains. To restrict illegitimate users or malicious attackers (such as worms) network analysts have suggested network access control (NAC). Specifically, we apply NAC to wireless sensor network epidemic models in order to investigate distribution density, transmission range and sensor area/field. Our analyses involved analytical expressions of two sensor fields gleaned from literature. Additionally, we explored the possibilities of infectivity of sensor nodes at the exposed class using the two expressions for sensor field topologies. We also derived the reproduction ratios and solutions at several equilibrium points for the models. It is our hope that that our work herein would impact sensor deployment decisions for organizations that utilize wireless sensor networks for meaningful daily activities.
Epidemic Theory, Wireless Sensor Networks, Network Access Control, Random Distribution
Короткий адрес: https://sciup.org/15016714
IDR: 15016714 | DOI: 10.5815/ijmecs.2017.11.06
Текст научной статьи Modeling the effect of network access control and sensor random distribution on worm propagation
Published Online November 2017 in MECS DOI: 10.5815/ijmecs.2017.11.06
The immense uses of Wireless Sensor Networks have made it a prominent technology of this era. This kind of networks mostly allows the random deployment of sensor nodes in un-trusted terrains without predetermined or engineered position. This emerging technology consists of miniaturized but low battery-powered devices that incorporate minimal sensing, processing, computation and radio transmission capabilities [1]. Its huge potential is evidently seen in its ability to provide dynamic and adaptable architectures for diverse applications in homes, healthcare, industry and in the military [1],[2]. Specifically, WSN applications are seen in the military
(for monitoring forces/equipments, battlefield surveillance, reconnaissance, targeting, battle damage evaluation); the home and in the environment (for biocomplexity mapping, precision agriculture, fire and flood detection etc) [1,3]. Its use extends also to health applications (for telemonitoring of data, tracking/monitoring of doctors/patients and drug administration) and other commercial applications [3].
As shown in Fig 1, WSNs are “multi-hop packet based networks”[4] that consists of sensor nodes which are distributed in a sensor field where they are wirelessly connected to the sink [5]. They track, record and send ambient territorial parameters to a data collector (or base station) through “multihop infrastructureless” transmission between neighboring sensor nodes. The communication done in the open air medium [4] and its deployment in un-trusted, unguarded and unfriendly terrain, makes the WSN an easy target to external attacks that seek to delay/disrupt legitimate flow of information. These attackers exploit other open challenges of the WSN such as finite bandwidth, computational power, storage, and communication range; packets’ authentication, and uncertainty (in mobility, topology control, density, sensing accuracy) [1,3]. Modern research-based developments in sensor networks indicate that a malevolent attacker can utilize several innards of sensor nodes to outspread malicious codes all through the network without physical contact or human intervention [6]. As Giannetsos et al. [6] puts it, “such a method is to exploit memory related vulnerabilities, like buffer overflows, to launch a worm attack”.
Attacks such as sinkhole, sybil, wormhole and hello flood in WSN are events that diminishes or eliminates a network's capacity to perform its expected function [7]; in other words these attacks deplete the confidentiality, availability and integrity (CIA) parameters of neighboring sensor nodes. To curb incidences of malicious code attacks in networks, analysts have proposed equation-based models to characterize, represent and understand spread patterns, strategies.
Often times the strength of particular model is determined by how much it can enhance understanding of malicious code transmission.
Fig.1. Wireless Sensor Networks Environment [32]
-
II. R elated W orks
Researchers in network security have discovered that there exist similar features between virus spread in biological networks and the propagation of malicious codes in telecommunication networks. With the development of the widely applied Susceptible-Infected-Removed (SIR) analytical model [8-10], the journey into investigating the infectious outcomes of a susceptible population in view of the interaction between “agent”, “host” and “environment” began. Usually referred to as “ Epidemic models” , these system(s) of equations that implement the epidemic theory can be ordinary differential, partial differential, or difference (depending on the intention of the modeler). Aside its application, in public health, they are also evident in the characterization of computer networks [11], peer-to-peer (P2P) [12], wireless sensor networks [13] and the WWW [14] or the internet [15].
To provide better understanding and to address security issues arising in the above networks, analysts have proffered (and involved) analytical solutions/suggestions to cater for the observed features of known malicious codes; they include inoculation, quarantine, time delay, effect of anti-malicious code softwares etc. Their suggestions are seen to be part of several models for instance the SIS, SEIR, SEIRS-V, SEIQR, SEIQRS-V etc.
In a bid to represent the temporal and spatial dynamics of worms spreading over a sensor network, Khayam and Radha [16] developed the topologically-aware worm propagation model (TWPM) that considered the distribution of stationary and identical sensors on a grid governed by a two-dimensional, discrete-time random process. Their analysis included the expressions for the effects of medium access control (MAC) layer contention, network layer routing and transport layer protocol and their impacts on worm spread in WSN. In a later publication, the Khayam and Radha [17] used signal processing technique and a more advanced mathematical treatment to model propagation of worms in a sensor network.
De, Liu and Das [18] assumed that malicious objects can starts its spread in a wireless sensor network due to either a compromised broadcast source or the lack of complex authentication schemes. In the light of this assumption they proposed an analytical model based on epidemic theory that involves the essential parameters of communication strategies of popular broadcast protocols such as Trickle, Deluge and MNP, so as to investigate speed and reachability.
Tang and Mark [19] considered the addition of a maintenance capability to a group of identical and uniformly distributed sensors in a geographical area. Therein, the SIR model is modified to SIR-M (i.e., SIR with Maintenance) in order to investigate the impact transmission range and distribution density.
Wang and Li [20] also modified the SIR model to iSIR model wherein the addition of the dead nodes (D) was considered; these are nodes who has exhausted their energy perhaps due to power consumption or due to malware activities. Simulation results of the iSIR model show that the process of worm propagation is sensitive to the topological structure of the network and the energy consumption of the sensor nodes.
Tang and Mark [19] and Wang and Li [20] did not consider the sleep and work interleaving strategy employed for elongating the lifetime of sensor nodes in WSN. This shortcoming is alleviated by the EiSIRS model developed by Wang, Li and Li [21] to practically analyze the dynamics of worm propagation, and this model considered sleep and work states.
The impact of medium access control (MAC) on the propagation dynamics of worm behavior was modeled by Wang and Yang [22] using the SI (Susceptible-Infected) model. Numerical simulations were used to show that increasing the network node density or the transmission range increased the number of infected nodes.
Though Mishra and Keshri [13] didn’t consider the sleep/work interleaving policy, their Susceptible-Exposed-Infectious-Recovered-Susceptible-Vaccination (SEIR-V) epidemic model involved the latent phase of malicious code spread (wherein the the usual speed of transmission of data become slow) and the inoculation of sensor nodes before the outset of malicious code (worm) infection.
Mishra, Srivastava and Mishra [23] proposed the Susceptible-Infected-Quarantine-Recovered-Susceptible (SIQRS) epidemic model and Mishra and Tyagi [24] proposed the Susceptible-Exposed-Infectious-Quarantine-Recovered with Vaccination (SEIQRS-V) epidemic model. Aside characterizing worm dynamics in WSNs, the symbolic solutions for the existent equilibrium states (worm free and endemic). Zhang and Si [25] proposed a delayed form of the SEIR-V epidemic model i.e. delay was used as the bifurcation parameter. To determine the direction of the Hopf bifurcation and the stability of the bifurcated periodic solutions, they used the normal form method and the center manifold theorem.
Even though Feng et al. [26] failed to consider the exposed state of worm dynamics as well as the vaccination of sensor nodes in WSN, their Susceptible-Infected-Recovered (SIR) epidemic model used the topological expression of Wang and Li [20] to study the effect of communication range, network node density and energy consumption. In addition the jacobian method was used to investigate the local stability while the lyapunov theorem was used to study the global stability.
On the other hand, to ensure network security some schools of thought have suggested Network Access Control (NAC) as a way of disallowing illegitimate users/nodes in WSNs [27,28]. According to Butun and Sankar [27], though NAC has been settled for traditional computer systems, it has not been investigated thoroughly in WSN scenarios. This is due to some inherent features/challenges of the sensor network which include open air communication, unreliable hardware, uniqueness/difficulty of access control, key renewal for newly deployed nodes and low-battery power. However, in traditional computer systems NAC has proved to be of immense benefits. For instance the CISCO version of NAC, called the Network Admission Control can harden a network, prevent network breaches, eliminates unauthorized network connections and identify, quarantine and remediate non-compliant/vulnerable devices in the network. Recently, a governing solution was derived for what seem like the NAC using classic epidemic models in [29]. This first order equation therein caters for quarantining and remediation of immigrant infected nodes through its Pre-quarantining compartment.
In this paper, we modify the Quarantine-Susceptible-Exposed-Infectious-Recovered-Susceptible with Vaccination (Q-SEIRV) epidemic model of [29] by applying Tang and Mark [19]’s expression for Sensor Field 1 and Wang et al. [20]’s expression for Sensor Field 2 . Additionally, we explored the possibilities of infectivity of sensor nodes at the exposed class using the two expressions for sensor fields/WSN topologies which represents uniform random distribution of sensor nodes. This is aimed at investigating the effect of distribution density, transmission range and NAC on worm propagation.
-
III. T he NAC SEIRS-V M odel
To accurately represent malicious code spread with respect to time in a sensor network we propose the inclusion of distribution density ( σ ), transmission range ( г2 ) in the Network Access Control-Susceptible-Exposed–Infectious–Remediated–Vaccinated (NAC-SEIRV) epidemic model. At first, we assume sensor nodes pass through a pre-screening process, where infectious immigrant nodes are isolated, treated and sent to the remediated compartment. This act of remediating infective sensor nodes closely mimics the “ Remedial ” nature of NAC. Sensor nodes that are free of any malicious code infection enter the susceptible sensor population. To a large extent the NAC applied here implements “ the assume guilty till proven innocent ” slogan of the cyber space. Inoculation of the susceptible sensor nodes provides additional immunization capability toward the outbreak of subsequent malicious code infections.
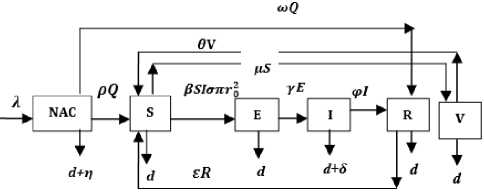
Fig.2. Schematic diagram for the proposed NAC-SEIRV model (as adapted from [29])
It is seen from the loop that the dynamics of the NAC compartment is governed by the first order differential equation:
Q = X- Q(d + л + p + to) (1)
The solution of this equation is derived from the convolution integral as:
Q (t) = e-(d+,? +p+to)tQ0 +
___________ [1 - g — (d+i? +p+w)t i (d+; +p+to) L J
Q0 is the initial population. Our assumptions on the dynamical transfer of the population in Sensor field 1 are depicted as Fig 2. From the schematic diagram a system of ordinary differential equations are generated and it goes thus;
S = pQ + 6V + eR - S(PIanr 0 + d + p)
E = pSIanr O - E(y + d)
I = yE - I(p + d + 6) (3)
R = oQ + pI — R(e + d)
V = pS-V(6 + d)
The assumptions on the dynamical transfer of the population using Sensor field 2 will affect equations for the susceptible and exposed class i.e. PSIanr O is replaced by PSIo кг 0 /E in the schematic diagram of Fig 2. The resulting system of ordinary differential equations are;
S = pQ + 6V + eR - S(PIonr 0 /L2 + d + p)
E = pSIanro/L2 - E(y + d)
I = yE -I(p + d + 6) (4)
R = oQ + pI — R(e + d)
V= pS-V(6 + d)
Given the above system of equation, the sensor nodes are uniformly and randomly deployed with a distribution density of о and a transmission range of г02 , this implies that the effective contact with an infected node for transfer of infection is in the order of аигО for Sensor field 1 and in the order of аигО /E for Sensor Field 2. Other parameters include; X = inclusion rate of nodes into the network population, p = infectivity contact rate, d = mortality or the death rate of nodes due to hardware or software failure, ] = death rate of infected immigrant nodes, 5 = is the crashing rate due to attack of worms, e is the rate of transmission from remediated class to susceptible class, p is the rate of transmission from quarantined to susceptible class, у is the rate of transmission from exposed to infectious class, to = rate of transmission from quarantine class to remediated class. p = rate of transmission from infectious to the remediated class, 6 = rate of transmission from vaccinating class to susceptible class, с is the vaccinating rate coefficient for the susceptible nodes.
-
A. Solution at Equilibrium Points
Equating the modified system of differential equations (3) to zero we obtain two solutions which are the worm-free equilibrium and the endemic equilibrium points. Hence, a worm-free equilibrium of the model that exists is the same for both sensor fields and it goes thus; W = (Sf,Ef,If,Rf , Vf) =
, ((З^Кс^^+^ф+^^+ш))) q q p+Qtd d(d+£)(d+9+p) d+£
p(dQ*(p+£(p+Q*((p+to))) x
d(d+£)(d+9+p)
Sensor Field 1 : At the endemic equilibrium there is presence of infection or disease i.e. worm in the wireless sensor network. Hence, an endemic equilibrium of the model exists at: We=
- * (d+y)(d+S+p) .
ДГ»ПГ 2 ’
E *
I * =
, d(d+y)(d+£)(d+0+p)(d+3+to)
(-^ ~ T^-^T---—-Q*(dp+£(p+ti)))(-d-3-p)
^y(d+e)snrQ
(d+y)(d+3)(d+£)+d(d+y+£)p
( dtf-yW-sW-e-y^^
Py(d+0)ffnrg
^^рК^^-^ ^-5^) -^)
Q^pp+Q4d+y)(d+8+p) M - d(d-')-^
P(d-6)onrQ (d+y)(d+5) (d+£)+d(d+y+£)p у * _ (d+yMd+S+p)
^y(d+9)Gnr 2
Sensor Field 2: Here, an endemic equilibrium of the model exists at: We=
$* _ L2(d+y)(d+S+p)
Дуапг 2
E *
I *
(П -dQ * (p-£(p+Q * ((p+«)))(-d-3-p)
(d (d-y^-eKd-S-p) e)
(n-dQ * (p-£(p+Q * ((p+«)))(-d-S-p) e^,^)/^ ^ "•"•" -■■)
R *
m , n*-.. , (^_-dQ^Op-eCoD-Q^CCp-co)))(-d-3-oD)
P+Q ("+ (d+5+p)((d-yM-e№-5-$)_£)
d+£
у * _ L2 (d+y)p(d+3+p) ^y(d+9)anr 2
Where
_ dL2(d+y)(d+£)(d+9+p)(d+S+p)
^y(d+9)anr 2
-
IV. T wo I nfectivity R ates
With the addition of an infectivity rate for the exposed class, the transfer for the susceptible class to the exposed class becomes something different. The system of differential equations for two infectivity rates is;
S = pQ + 6V + eR - S(nEanr 0 + pianr ^ + d + p) E = nSEanr 0 + pSIanr 0 - E(y + d)
I = yE - I(p + d + 5) (8)
R = toQ + pI — R(e + d)
V= pS-V(6 + d)
Where П is the infectivity rate of the sensors in the exposed class. The solutions for the endemic equilibrium points when the infectivity rates of the exposed and the infectious sensors are considered are slightly different from the (6). Note that at the worm-free equilibrium the solutions are the same with (5). Here the endemic equilibrium of the model (using sensor field 1) exists at: W e =
E * =
I * =
s* _ (d+y)(d+S+p)
(^y+n(d+6+p))anr 2
(d+£)+(-d-6-p)(-£(p+Qы)(Ф-Qp))
d3+y£(-1+6+p)+d2(y+S+£+p)+d(£(6+p)+y(S+£+p)) y(-d-6-p)(-£(p+Qы)+(d+£)(-Qp+Ф))
Y (d3+y£(-1+S+p)+d2(y+S+£+p)+d(£(6+p)+y(6+£+p)))
R *
+ 0 M+_______y(-d-6-p)(-£(p+Qш)+(d+£)(Ф-Qp))_______ p Y(d3+y£(-1+3+p)+d2(y+3+£+p) + d(£(3+p)+y(3+£+p)))
d+£ у * _ (d+y)p(d+S+p)
(d+9)(^y+n(d+S+p))Gnr 2
Where
d(d+y)(d+9+p)(d+3+p)
Y = (d + 5 + p),Q--г
(d+9)(^y+n(d+S+p))Gnr 2
The endemic equilibrium of the model (using sensor field 2) exists at: We=
E *
^* _ L2(d+y)(d+S+p)
(^y+P(d+5+p))anr 0 ((d+£) (P-Qp)—£(p+Qti))(—d—S—p)
d3+y£(-1+5+p)+d2(y+5+£+p)+d(£(5+p)+y(5+£+p)) I * =
((d+£)(P-Qp)-£(p+Qti))y(-d-5-p)
(d+S+p)(d3+y£(-1+S+p)+d2 (y+5+£+p)+d(£(5+p)+y(5+£+p))) R * =
. 0 ,___________ y(-d-3-p)(-£(p+Qш)+(d+£)(-Qp+P)) ___________
P (d+3+p)(d 3 +y£(-1+3+p)+d 2 (y+3+£+p)+d(£(3+p)+y(3+£+p)))
d+£ у * _ L2(d+y)p(d+S+p)
(d+9)(^y+n(d+S+p))Gnr 2
-
A. Reproduction Ratio
The reproduction ratio is “the expected number of secondary cases produced in a completely susceptible population, by a typical infective individual” [30]. Mishra & Pandey [31] refers to is as the as the inverse of the susceptible at the endemic equilibrium. Going by that, the reproduction number at both sensor fields is given as;
Sensor Field 1: R 0 =
РУ<™т 0 (y+d)(p+d+6)
Sensor Field 2: R 0 =
0Y<™r 0 L2(d+y)(d+S+p)
When sensors in the exposed class possess a different infectivity rate lesser than that of the fully infectious nodes then the model’s reproduction ratio would certainly differ from (11) and (12). Using the expression for sensor field 1 the reproduction number/ratio is (13) while the reproduction ratio for sensor field 2 is (14).
TIme
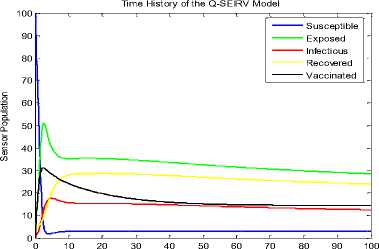
Fig.4. Time History at r=2 and □ = 0.3 for NAC-SEIRV
Sensor Field 1: R0 =
(pY+n(d+6+p))anr 2 (d+y)(d+6+p)
Sensor Field 2: R0 =
(pY+n(d+6+p))anr 2 L2(d+y)(d+S+p)
V. S imulation R esults for NAC–SEIRV E pidemic M odel
We present the numerical results using Runge-Kutta Fehlberg method of order 4 and 5 for the NAC-SEIRV model. The network is assumed to have initial values: Qo = 5; S=100; E=3; I=1; R=0; V=0. Other values used for the simulation include Л =0.33; p =0.3; to =0.01; T = 0.001; e = 0.3; P = 0.1; у =0.25; p =0.4; d = 0.003; 5 = 0.07; 6 = 0.06; p = 0.3; adapted from the time history of [29].
A. Sensor Field 1
We observed that at r=1, the responses are the same for the time histories of [29] (Fig. 3) and NAC-SEIRV (Fig. 4). At r =2 in Fig. 4, the number of exposed sensor nodes shot up to 51 from the initial 35 exposed sensor nodes at r =1. Gauging the distribution density and the range alongside our aznalytical NAC presents some interesting factors worthy of note. Comparing Fig. 7 of [5] and Fig. 5 shows the impact of NAC. At density = 0.3, r =2 and at density = 0.5, r =2; the exposed nodes of Fig. 7 is 65 and 72 while the exposed of Fig. 5 is 51 and 53. Even keeping density constant at 0.5 and increasing r from 2.0 to 2.5 showed the impact of NAC because the 79 exposed nodes recorded in Fig. 7 was reduced to 57 exposed nodes in Fig 5.
The impact of NAC becomes more evident if one considers the behavior of the recovered class for the model in [29] (Fig. 3) and Fig. 4. While the recovered class is at 19 sensor nodes for Fig. 3, the recovered class appreciated for Fig. 4 (i.e. it became 28 sensor nodes).
To further show the effect of NAC, we employ the results of Nwokoye et al. [5] where there was a notable increase in the exposed class (Fig. 7) and a decrease of the vaccinated class (Fig. 8). Keeping density constant at 0.5 and increasing from 2.0 to 2.5 showed the impact of NAC because the 79 exposed sensor nodes recorded in Fig. 7 was reduced to 57 exposed nodes in Fig. 5. At density = 0.3, r =2 and at density =0.5, r =2; the vaccinated nodes of Fig. 8 is 12 and 15 while the vaccinated of Fig. 5 is 30. Keeping density constant at 0.5 and increasing the transmission range from 2.0 to 2.5 showed the impact of NAC because the 21 vaccinated sensor nodes recorded in Fig. 8 increased to 35 exposed nodes in Fig 6. This implies that increase in worm infection can be tackled using the NAC.
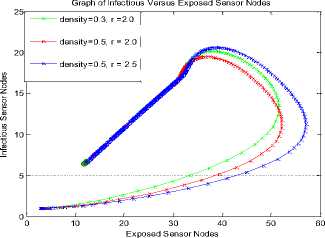
Fig.5. Infectious vs Exposed for NAC-SEIRV
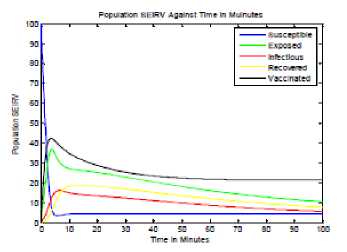
Fig.3. Time History adapted from [29]
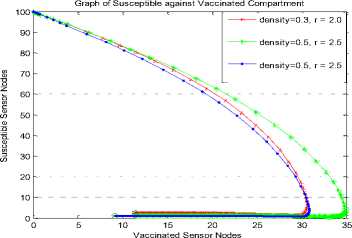
Fig.6. Susceptible vs Vaccinated for NAC-SEIRV
Graph of Infectious Nodes Plotted against Exposed Nodes
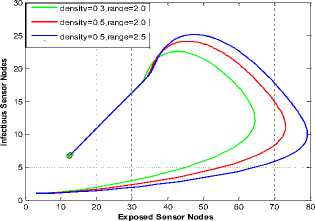
Fig.7. Infectious vs Exposed [5]
There was no difference between the simulation experiments that represent the presence (Fig. 9, Fig. 10) and absence of NAC (Fig 11, Fig 12).
Graph of Sensor Population (WITHOUT NAC) 100
Susceptible Exposed Infectious Recovered Vaccinated
Graph of Susceptible Nodes Plotted against Vaccinated Nodes
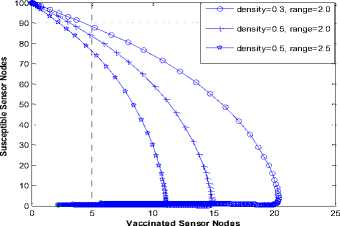
Fig.8. Susceptible vs Vaccinated [5]
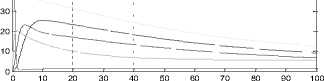
TIme
Fig.11. Time History at r =1, L = 0.5 (Without NAC)
B. Sensor Field 2
To simulate the network (for Sensor Field 2), we employ the same initial values used for NAC–SEIRV Epidemic Model (Sensor Field 1).
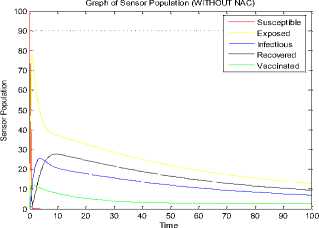
Fig.12. Time History at r =1.5 and L = 0.5 (Without NAC)
Grpah of Sensor Population
Susceptible Exposed Infectious Recovered
Vaccinated

Time
Fig.9. Time History at r =1 and L = 0.5 (NAC)
C. Two Infectivity Rates
We assume the following initial values for the network; S=100, E=1, I=1, R=0, V=0. Note that since the exposed sensor nodes have been adjudged infectious i.e. possessing some infectivity rate, we reduced the initial value for the exposed class to 1. The result of the modification of system of equation (8) is shown as Fig. 13. This figure is similar to the case of vertical transmission described in Nwokoye, et al [33]; wherein the exposed class increased due to the birth of a fraction of the exposed and the infectious nodes.
Graph of Sensor Population against Time
Susceptible Exposed Infectious Recovered
Vaccinated
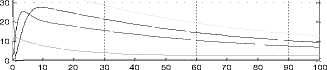
TIme
Fig.10. Time History at r =1.5 and L = 0.5 (NAC)
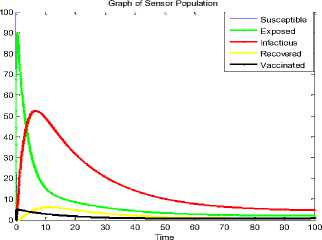
Fig. 13. Time History at Л=0.33, г=0.3, (=0.5, П=0.2, y=0.25, ^=0.02, d=0.003, 5=0.07, 6=0.06, ц=0.3, <7=0.3, r=1
From our simulation results, it is obvious that increasing the value of r and keeping L constant, increased the number of exposed nodes and reduced greatly the number of vaccinated nodes. On the other hand, NAC has no effect in Sensor field 2. This is clearly seen if one considers Fig. 9, Fig. 11 and Fig. 10, Fig. 12.
Note that aside the infectivity rate of the exposed class, the range and density also contributes to the probable cause for epidemic in the sensor network.
On the other hand, we performed simulation experiments in order to observe the impact of NAC when the infectivity rates of the exposed and the infectious sensor nodes are considered. More so the impacts of NAC are shown using the dynamic behavior of the recovered class. Fig. 14 and Fig. 15 show the dynamical behavior of the SEIR-V model (with two infectivity rates) without NAC and with NAC respectively, at the same recovery rate (0.4). From the two figures (simulated with the values of Fig. 13, excepting p), it is evident that persistent recovery of the sensors is more likely with the latter (Fig. 15). Specifically, while the recovered class was 27 sensor nodes for Fig. 14 (without NAC), the recovered class was 35 sensor nodes for Fig 15 (with NAC).
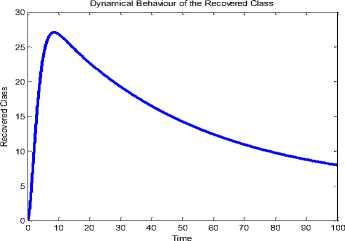
Fig.14. Time History of the (Two Infectivity Rate Model) at p=0.4.
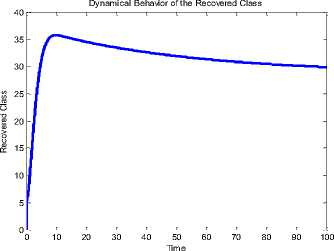
Fig.15. Time History of the (NAC Two Infectivity Rate Model) at p=0.4
Fig. 14 and Fig. 15 are the results of our modification using sensor field 1. Since the length of side ( L2 ) distinguishes sensor field 1 from sensor field 2, it is necessary to observe its impact on the recovered class of sensor nodes.
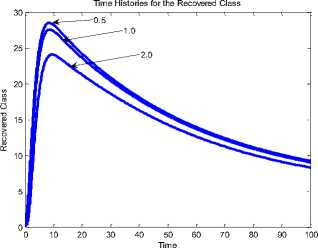
Fig.16. Time History of the Recovered Class at L2 = 0.5, 1.0, 2.0 (Without NAC)
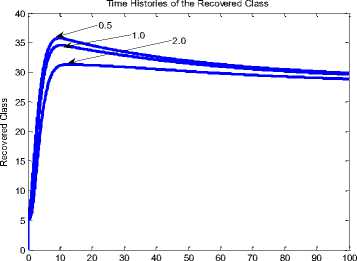
Time
Fig.17. Time History of the Recovered Class at L2 = 0.5, 1.0, 2.0 (With NAC)
Fig. 16 shows the impact of length of side on the SEIR-V model (without NAC). It is evident that the sensor nodes in the recovered class reduced as the length increases (from 0.5 to 2.0). This is so with Fig 17 (with NAC)
VI. C onclusion
Our study here explored the characterization/application of network access control (NAC) to epidemic models in wireless sensor networks; considering random distribution of nodes in two different types of sensor fields. The first sensor field was proposed by Tang and Mark [19] while the second one was proposed by Wang, et al. [20]. We believe that NAC may to some extent remediate immigrant infected nodes; thereby reducing the importation of infections through sensor node addition. Other insights on the factors that increase the node exposure or infectiousness was also highlighted using several simulation experiments of both sensor fields. More so we derived the reproduction ratio of both sensor fields in all the cases x-rayed by our study herein. Firstly, is the case where only the infectious class possess infectivity and secondly, the case where both the exposed and infectious class possess infectivity.
We observed the impact of NAC when our model (for Sensor field 1) herein was compared with an equivalent model in literature. Specifically, NAC reduced the exposed and the infectious compartment. Correspondingly, it improved the vaccination countermeasure.
Conversely, the topology described in [20, 26] (Sensor field 2), was not impacted by NAC if one consider the behavior of exposed, the infectious and the vaccinated class. We feel the reason was due to the addition of the length of side ( L ). This parameter is non-existent in Sensor field 1 [19]. The rationale for using [5] for comparative analyses in NAC-SEIRV for sensor field 1 was because the work has already highlighted the negative impact of increasing both density and range in the network. Furthermore, we noticed that increasing the value of r and keeping L constant, increased the number of exposed nodes and reduced greatly the number of vaccinated nodes.
On the case of infectivity at both the exposed and infectious class (described with the simulation results of section V, subsection C ), we observed a better recovery of the sensor network. However, it is clear that NAC is not entirely an almighty solution to a worm-laden sensor network i.e. network managers should entrench practices that increase the recovery tendencies of sensors. Then with the addition of NAC the network becomes fortified against external importation of infection. Additionally, the length of side impacted the recovered class for both sensor fields.
The above analyses will impact sensor deployment decisions in organizations that use wireless sensor networks. Specifically, it will inform them on the factors that inhibit/aid worm propagation. Furthermore, we would apply other network characteristics/protocols in order to check its effect in worm propagation and containment.
A cknowledgment
We thank the anonymous reviewers that read our manuscript and their keen efforts directed at ensuring accuracy of our work.
Список литературы Modeling the effect of network access control and sensor random distribution on worm propagation
- I. F. Akyildiz, W. Su, Y. Sankarasubramaniam and E. Cayirci, “Wireless sensor networks: A survey”, Computer Networks, vol. 38, 4, pp. 393–422, 2002.
- D. Buch and D. Jinwala, “Prevention of wormhole attack in wireless sensor network”, International Journal of Network Security & Its Applications (IJNSA), vol. 3, pp. 85–98, 2011.
- C. H. Nwokoye, I. Umeh, M. Nwanze, B. F. Alao, “Analyzing time delay and sensor distribution in sensor networks”, IEEE African Journal of Computing & ICT 8, vol. 1, pp. 159–164, 2015.
- A. Gupta and A. K. Gupta, “A survey: Detection and prevention of wormhole attack in wireless sensor networks”, Global Journal of Computer Science and Technology: E Network, Web & Security, vol. 14, pp. 23–31, 2014.
- C. H. Nwokoye, V. E. Ejiofor, R. Orji, I. Umeh and N. Mbeledogu, Investigating the effect of uniform random distribution of nodes in wireless sensor networks using an epidemic worm model”, Proceedings of the 2nd International Conference on Computing Research and Innovations (CoRI’16), pp. 58–63, 2016.
- T. Giannetsos, T. Dimitriou and N. R. Prasad, “Self-propagating worms in wireless sensor networks”, ACM CoNEXT - Student Workshop’09, pp. 31–32, 2009.
- U. Narayanan and A. Soman, “Attack and counter measurement of worm hole and false data injection in wireless sensor networks: A survey. International Journal of Advanced Research in Computer and Communication Engineering, vol. 2, pp 2–6, 2013.
- W. O. Kermack and A. G. McKendrick, "A Contribution to the Mathematical Theory of Epidemics," Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, vol. 115, pp. 700–721, 1927.
- W. O. Kermack and A. G. McKendrick, "Contributions to the mathematical theory of epidemics. ii. the problem of endemicity," Proceedings of the Royal Society of London. Series A., vo1. 38i834, pp. 55–83, 1932.
- W. O. Kermack and A. G. McKendrick, "Contributions to the mathematical theory of epidemics. III. Further studies of the problem of endemicity," Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, vol. 141, pp. 94–122, 1933.
- B. K. Mishra and D. K. Saini, “Mathematical models on computer viruses”, Applied Mathematics and Computation, vol. 187, pp. 929–936, 2007.
- T. Richard and C. Mark, “Epidemiological modelling of peer-to-peer viruses and pollution”. Proceedings - IEEE INFOCOM, 2006.
- B. K. Mishra and N. Keshri, "Mathematical model on the transmission of worms in wireless sensor network," Applied Mathematical Modelling vol. 37, pp. 4103–4111, 2013. http://doi.org/10.1016/j.apm.2012.09.025
- L. Chunbo and J. Chunfu, “Modeling passive propagation of malwares on the WWW”, Physics Procedia, vol. 33, pp. 271–278, 2012.
- Y. Yao, L. Guo, H. Guo, G. Yu, F. X. Gao and X. J. Tong, “Pulse quarantine strategy of internet worm propagation: Modeling and analysis”, Computers and Electrical Engineering, vol. 38, pp. 1047–1061, 2012.
- S. A. Khayam and H. Radha, "A topologically-aware worm propagation model for wireless sensor networks", 25th IEEE International Conference on Distributed Computing Systems Workshops, IEEE, pp. 210–216, 2005.
- S. A. Khayam and H. Radha, "Using Signal Processing Techniques to Model Worm Propagation over Wireless Sensor Networks," IEEE Signal Processing Magazine, pp. 164–169, 2006.
- P. De, Y. Liu, and S. K. Das, "An epidemic theoretic framework for evaluating broadcast protocols in wireless sensor networks. 2007 IEEE International Conference on Mobile Adhoc and Sensor Systems, IEEE, pp 1–9, 2007.
- S. Tang and Brian L. Mark, "Analysis of virus spread in wireless sensor networks: An epidemic model," Proceedings of the 2009 7th International Workshop on the Design of Reliable Communication Networks, DRCN 2009: pp. 86–91, 2009. http://doi.org/10.1109/DRCN.2009.5340022
- X. Wang and Y. Li, "An improved SIR model for analyzing the dynamics of worm propagation in wireless sensor networks," Chinese Journal of Electronics, vol. 18, 2009.
- X. Wang, Q. Li, and Y. Li, "EiSIRS: A formal model to analyze the dynamics of worm propagation in wireless sensor networks," Journal of Combinatorial Optimization, vol. 20, pp. 47–62, 2010. http://doi.org/10.1007/s10878-008-9190-9
- Y. Wang and X. Yang, "Virus spreading in wireless sensor networks with a medium access control mechanism," Chinese Physics B, vol. 22, 40200-40206, 2013. http://doi.org/10.1088/1674-1056/22/4/040206
- B. K. Mishra, S. K. Srivastava, and B. K. Mishra, "A quarantine model on the spreading behavior of worms in wireless sensor network. Transaction on IoT and Cloud Computing, vol. 2, pp. 1–12, 2014.
- B. K. Mishra and I. Tyagi, "Defending against malicious threats in wireless sensor network: A mathematical model", International Journal of Information Technology and Computer Science, vol. 6, pp. 12–19, 2014.
- Z. Zhang and F. Si, "Dynamics of a delayed SEIRS-V model on the transmission of worms in a wireless sensor network," Advances in Difference Equations: pp. 1–15, 2014. http://doi.org/http://www.advancesindifferenceequations.com/content/2014/1/295
- L. Feng, L. Song, Q. Zhao, and H. Wang, “Modeling and stability analysis of worm propagation in wireless sensor network. Mathematical Problems in Engineering, 2015.
- I. Butun and R. Sankar, “A brief survey of access control in wireless sensor networks”, The 8th Annual IEEE Consumer Communications and Networking Conference, pp. 1118–1119, 2011.
- Y. Zhou, Y. Zhang, and Y. Fang, “Access control in wireless sensor networks”, Ad Hoc Networks, vol. 5, pp. 3–13, 2007.
- C. H. Nwokoye, V. E. Ejiofor and C. G. Ozoegwu, "Pre-Quarantine approach for defense against propagation of malicious objects in networks," International Journal of Computer Network and Information Security (IJCNIS), vol. 9, pp. 43-52, 2017. doi:10.5815/ijcnis.2017.02.06
- O. Diekmann, J. A. P. Heesterbeek and J. A. J. Metz, “On the definition and the computation of the basic reproduction ratio r0 in models for infectious diseases in heterogeneous populations. Journal of Mathematical Biology, vol. 28, pp. 365–382, 1990.
- B. K. Mishra and S. K. Pandey, "Dynamic model of worms with vertical transmission in computer network," Applied Mathematics and Computation, vol. 217, pp. 8438–8446, 2011.
- S. Yinbiao, K. Lee and P. Lanctot, “Internet of Things:Wireless Sensor Networks, 2014.
- C. H. Nwokoye, V. E. Ejiofor, M. O. Onyesolu and B. Ekechukwu,"Towards modeling malicious agents in decentralized wireless sensor networks: a case of vertical worm transmissions and containment", International Journal of Computer Network and Information Security (IJCNIS), vol.9, pp.12-21, 2017. DOI: 10.5815/ijcnis.2017.09.02.


