Modeling thermal conditions of the process combined rolling-extruding

In the implementation of the process combined rolling-extruding (CRE), like any other continuous process of metal forming, important to create thermally stable conditions of the instrument – rolls and matrix, well as ensuring a constant temperature of the product outlet of the matrix channel [1,2]. Further industrial development of this new way metal forming is constrained because of the lack of theoretical studies of the thermal conditions of the process. Therefore the analysis of the thermal interaction at CRE in order to create a mathematical model of calculation thermal conditions is actual task. The scheme of thermal interaction is shown in Fig. 1.

Deformation zone during CRE can be divided arbitrarily into three characteristic zones: rolling, decompression and extruding, differing in intensity heat release but similar in nature of action heat sources. In the volume of each zone operates volumetric heat source from plastic form changing of power with density q v , and at the contact boundary of a deformable metal and rolls permanent acting source of heat from external friction with density q_r .

Due to the high thermal conductivity of non-ferrous metals and alloys, small cross size of the deformation zone compared with the size of the rolls it can be assumed that the temperature at all points of the cross section of a deformable metal is identical and changes only along the length of deformation zone.

At the value of the Peclet number Pe = v Д l Д / a ≥10, and at CRE Pe ≥100, then, without much error heat propagation can be taken into account only in the direction normal to the surface of the contact of bodies, that is, the problem can be reduced to one-dimensional. Due to the fact that on contact surface

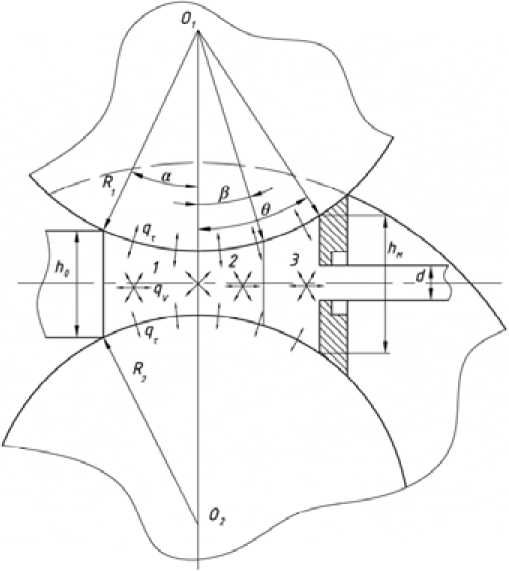
Fig. 1. The scheme of thermal interaction at CRE: 1 – rolling zone; 2 – decompression zone; 3 – extruding zone

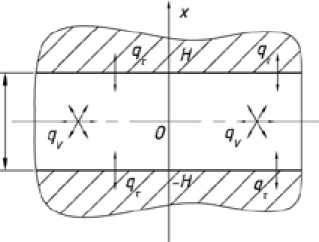
Fig. 2 Scheme to the calculation of the temperature conditions of the process CRE of the deformable metal and working instrument time of thermal interaction at CRE is small enough, and the heat does not have time to spread to a considerable depth, is possible, without compromising the accuracy of the final results, we neglect the curvature of the rolls on the arc length of the capture zone of rolling. Therefore, to solve the problem the deformation zone and rolls can be represented as bodies of classic shape: deformable metal in the form of an infinite plate with thickness 2H, and rolls – in the form of semi-infinite spaces (Fig. 2).

Place the origin of coordinates in the middle of the plate. Then the conditions of the problem in a mathematical form can be written as a system of two differential equations of unsteady heat conduction:

■ ai^Г^-^^ + ±- = 0, at 0< x<^Н|, dx          dt      cxpx 52T2 (x, t) 5T2 (x, t) n In                             ( ) a 2    2\ ’     2\    = 0,at ± Н < x < ±^ , t > 0, оx         Оt with the following boundary conditions:

' T 1( x ,0) = Т 10 ,     T 2( x ,0) = T 20 , T 1 ( ± H , t ) = T 2( ± H , t ), T 2 ( да , т ) - limited, (2) — ^Щ ( хг) =      at , = ± 0x         0x d T ( x , t ) Л. —-—- = 0,  at x = 0. d x

To solve the problem of unsteady heat conduction applied the analytical method of Laplace integral transforms. This method has several advantages over other classical methods thanks to standard methods of application and receipt of the decision in a convenient form for calculation and theoretical analysis. A result of solving problem is analytical dependence of the temperature distribution in a deformed metal and instrument:

T(x a — 2 qr \ierfc(H—) + ierfd H + x 4 qVt ___iderfc(H__—) + T 1 ( x , t ) =               [ ierjc ) 1 ierfc )]                   [ i erfc (        ) + b 2 ( k+ 1)      2 4a1        2 4a   c , p , (k + 1)       2 4a + i2 erfc ( H + x )] - ^ T ^ [ erfc ( H—x ) + erfc ( H + x )] + q V t- + T10 , 2 da.t     k 1 + 1       2 Ja.t          2 Ja.t     C i Pi T 2 ( — , . ) =   ^q V k'' ,, [ i’«rfc ( x - H ) -i’erfc (-^ - x - H )] + 2^ierfc ( x - H ) -         (3) c 1 P i( k 1 +1)      2 V a 2 7        V at 2 4a 5      b 2       2 4a 5 -    2ЛЛ [ ierfc ( Х - H - ierfc ( H + —-H )] + ^ Т к к 1 [ erfc ( X - H ) - k i + 1        2 J a 2 t        Jaf  2 J a 2 t    k , + 1       2d a 2 t -    erfc ( 2L + X - H )] + t 20 . V a 1 t   2 V a 2 2

Rolling zone (index α ), decompression zone (index β ) and extruding zone (index θ ) have the same character of the heat sources. In the volume of each zone operates volumetric heat source of plastic form changing of power density q v (Fig. 1). At the contact boundary of deformable metal (index 1) and rolls (index 2) permanent source of heat from external friction with density q τ . During the passage of a deformable metal working channel of the matrix (index 3) volumetric heat sources are absent, and at the contact boundary with the matrix are only sources of heat from external friction forces q τ . Average outlet profile temperature based on the additivity property of Fourier equation will be equal to the temperature changes during the passage of a deformable metal above the thermodynamic typical zones at CRE:

T1П (ti П) = To + А Т to (At to) + Атie (A11в) + А Т i6 (A116) + А Т,„ (At,„),                             (4) where T10 – initial temperature of the billet heating;

t iП = A t 1 a + A t 1 в + A t_X6 + A t 1 М ^- total time of deformation elementary unit;

А Т a ; А Т i , ; А Т i , ; А Т , „ ^- temperature change of elementary block during the passage of thermodynamic zones at CRE: rolling, decompression, extruding and squeezing through the working channel of the matrix accordingly;

I         АГ                 Аг АTi, =----[-f4qi(H,t)dt +J qv(t)dt]. Ci Pi V, 0                0 (5) 4[ qi( H, г )dt   k1 + 1{ qTk 1At,[l 4 2rrfc (^a---.)] c^pV 2    4 г 3rfcc( ^-a__ )] -bbi-Tb J- [ 1 -ierfc ( H )]}. К       a- Аг, (6) bi= λiciρi;λi;ai – coefficients of heat accumulation, thermal conductivity and thermal diffusivity; ci, ρi – heat capacity and density of billet materials (index 1) and rolls (index 2);

k ₁ = b ₁ b ₂; Δ T_B = T ₁₀ - T ₂₀ ; Т 10 and Т 20 – initial temperature of heating the billet and rolls;

q_τ and q_v – density of the heat sources at the surface and in the volume of billet;

Δt1М ППР            2ΔTМПР ⋅b1 ΔТ1М=с1ρ1FПР(k3+1)(qτM⋅k3-π⋅Δt1М ), (7) where Ппр and Fпр – perimeter and area of profile; Δt1М = FПРhСР , vМСРhγ2bK (8) where hср – the average height of matrix’s calibration belt;

ν МСР – average speed of deformable metal;

ΔТ _МПР – the temperature difference between the profile and matrix;

q τМ = µ Мvprof σ Sθ ,

(9)

μ М – coefficient of friction on the surface of matrix’s calibration belt;

ν _pro f – average speed of deformable metal outlet channel of the matrix;

σ S θ – average deformation resistance of metal in extruding zone.

With the application of the obtained dependences developed an algorithm for calculating the change in temperature of the metal and instrument at CRE, which was implemented in the program Microsoft Exel . The program allows at discrete input data to determine the temperature conditions of the process CRE.

The calculation results in graphs for aluminum alloys are shown in Fig. 3. In zones of rolling and decompression temperature of deformable metal decreases due to intense heat exchange with rolls. In extruding zone, on the contrary, there is a fairly sharp increase in temperature and achieve its maximum value at the exit from the channel of matrix through more intensive heat strain during extrusion profile.

Results of the research were used to select the optimal temperature and speed regimes during pilot testing, as well as in the rod development production technology of aluminum alloy by method CRE.

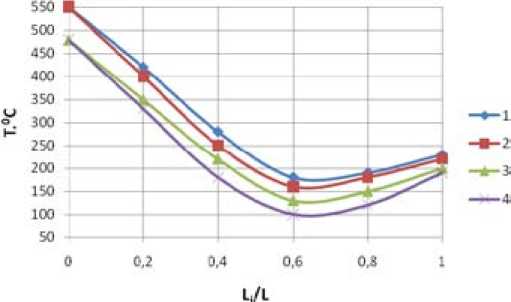
Fig. 3 The temperature change of deformable metal along the deformation zone during the production of rod from alloy АV93 at initial temperature of heating billet T 10 = 480°C and 550 °C rolls T 20 = 150 °C with different deformation speed of deformable metal (ξ): 1 – T 10 =550°C, ξ=1,49 s^-1; 2 – T 10 =550°C, ξ=0,74 s^-1 ; 3 – T 10 =480°C, ξ=1,49 s^-1; 4 – T 10 =480°C, ξ=0,74 s^-1