Моделирование

Моделирование крупногабаритных трансформируемых и надувных конструкций рефлекторов является актуальным направлением разработки и создания конструкций систем спутниковой связи и зондирования поверхности Земли, так как экспериментальная отработка подобных конструкций требует больших материальных и временных затрат. Для решения современных задач требуются все более крупногабаритные антенны с высокой точностью формы зеркала рефлектора. Разработка таких конструкций, позволяющих улучшить качество приема и увеличить размеры зон сканирования, является одной из главных целей в области космических программ. Основные требования к конструкциям рефлекторов заключаются в высокой точности формы отражающей поверхности и наведения, высокой температурной стабильности и радиоотражающей способности антенных систем.

Модель надувного рефлектора ARISE, разрабатываемая компанией L’Garde, Inc, представлена на рис. 1 [1].

Рис. 1. Проектная модель надувной антенны ARISE

Задача о напряженно-деформированном состоянии подобных вантово-оболочечных конструкций формулируется с позиций нелинейной теории упругости и в вариационной постановке [2]. Решение задачи осуществлялось методом конечных элементов [3].

Связь деформаций с перемещениями рассматривается в виде eaP = (1/2)( u a,p + u p,a + u 6,a u 9JS )•

Компоненты тензора напряжений Кирхгофа и компоненты тензора деформаций связаны следующей зависимостью:

ij j “в          T

° = a ( e aP e “P ) •

Элементы матрицы упругости, зависящие от принадлежности к разнородным элементам конструкции и уровня предварительных напряжений рассчитываются по формуле ij “P = nkkl        (0)j a — a ( x , о ).

Компоненты тензора температурных деформаций имеют вид e^A T3ap.

Для конструкций рефлектора граничные условия в перемещениях задаются на части поверхности Su конструкции рефлектора, где имеет место крепление к космическому аппарату u = u на внешней части поверхности конструкции Ѕp в условиях космического пространства о6jnj (5 ij + ui, j) = 0.

При моделировании наземных условий выполняется равенство

°6nJ(5 i+ uU) = P а’ где pa– атмосферное давление на поверхности Земли.

Таким образом, при известном температурном поле в элементах конструкции рефлектора задача МДТТ считается поставленной в замкнутой форме, так как количество определяемых функций перемещений соответствует количеству разрешающих уравнений. Для надувных конструкций на внутренних поверхностях надувных элементов, где действует давление газа p , имеет место краевое условие

° ⁶ n j^{( 5} j ⁺ u j = P j .

Аналитическое решение подобных задач представляется затруднительным. Для получения приближенных численных решений выгоднее опираться на вариационные постановки:

J { ( a j “^e ( e _ap- e T, ) ) 5 e , - P -5 r } d V - j ( p ₂ - p , ) n -5 r • dS ,

VSp ₁

где P – вектор массовых сил; F – вектор поверхностных сил.

Трехмерная модель надувного космического рефлектора, построенная в программном комплексе ANSYS, представлена на рис. 2. За основу взята модель надувной антенны ARISE (см. рис. 1).

Исходным состоянием является конфигурация рефлектора, вытекающая из технического задания с нулевыми напряжениями в элементах конструкции. После задания требуемых краевых условий в элементах конструкции получается напряженная конфигурация, находящаяся в состоянии статического равновесия и обеспечиваю- щая с достаточной точностью проектируемую форму отражающей поверхности рефлектора. Перемещения точек конструкции и возникающие в материале напряжения после приложения нагрузки в нашем случае давления показаны на рис. 3 и 4.

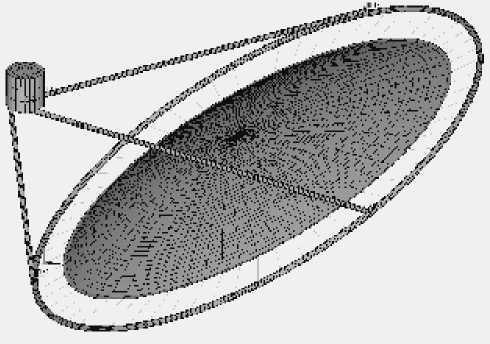
Рис. 2. Конечно-элементная 3D-модель надувного рефлектора

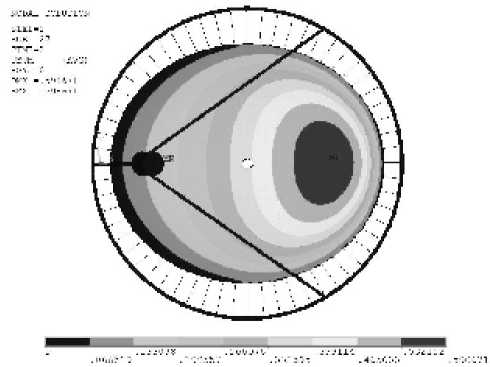
Рис. 3. Отклонения точек конструкции относительно начального ненапряженного состояния

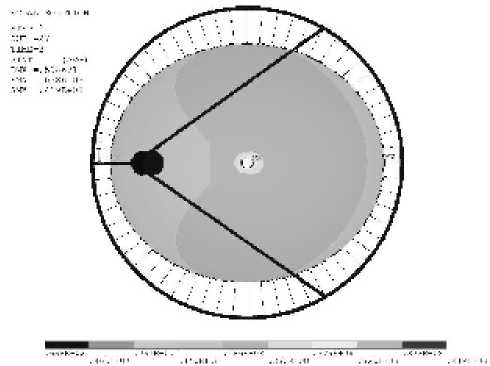
Рис. 4. Напряжения в элементах конструкции отно сительно начального ненапряженного состояния

Из проведенных вычислений следует, что основная нагрузка приходится именно на купол рефлектора, что объясняется значительно меньшей толщиной материала (рис. 3, 4). Исходя из этого и учитывая, что наиболее жесткие требования выдвигаются к отражающей поверхности, в дальнейшем будем рассматривать только ее с целью сокращения объемов вычислений.

Компьютерное моделирование показывает, что для оболочечных надувных конструкций имеет место масштабный фактор. Одной стороной его проявления является то, что при увеличении диаметра рефлектора и при уменьшении давления в куполе мы наблюдаем увеличение перемещений точек отражающей поверхности рефлектора относительно идеального параболоида.

Графики, на которых изображены перемещения точек отражающей поверхности в зависимости от радиуса конструкции при одинаковом значении давления в куполе и толщине материала, из которого он изготовлен, приведены на рис. 5.

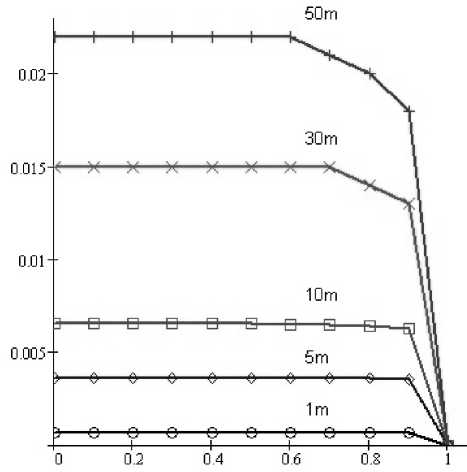
Рис. 5. Зависимости относительных перемещений точек отражающей поверхности от радиуса конструкции. По оси Y – перемещения, отнесенные к радиусу конструкции, по оси X – безразмерный радиус. Давление p = 10 Па; толщина пленки h = 900 мк; a – радиус конструкции

При надувании подобных конструкций в материале возникают сжимающие напряжения, приводящие к искажению формы отражающей поверхности на краю купола (рис. 6). Чтобы избежать искажения отражающей поверхности по периметру надувного купола, в радиальном направлении прикладывается внешняя растягивающая сила F , которая в реальной конструкции есть силовое воздействие от окружающего тора.

Зависимость приложенной по периметру в радиальных направлениях растягивающей погонной силы F , при которой в материале остаются только растягивающие напряжения, отнесенной к толщине материала h , из которого изготовлен купол, и модулю упругости, от диаметра конструкции изображена на рис. 7.

Зависимость напряжений, возникающих в материале надувного купола, от величины, приложенной растягивающей погонной силы, приводится на рис. 8.

Взяв только нижнюю часть купола и закрепив его по периметру, посмотрим, как меняется геометрия отражающей поверхности, и какие напряжения возникают в материале.

Рис. 6. Краевые искажения отражающей поверхности надувного рефлектора при внутреннем давлении 10 Па (для наглядности перемещения увеличены в 2 раза)

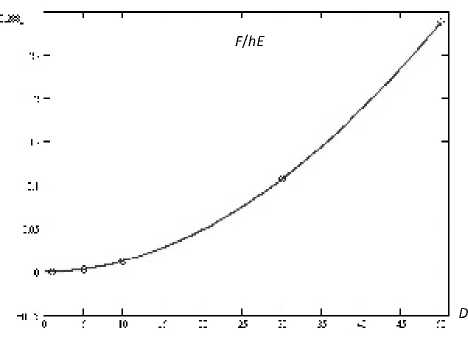
Рис. 7. Зависимость приложенной растягивающей силы для удаления искажений отражающей поверхности ( F / hE , где h = 0,000 9 м) от диаметра конструкции

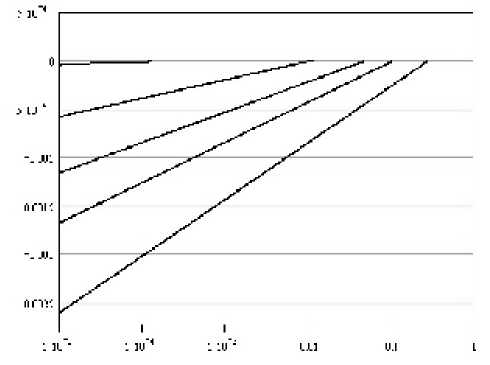
Рис. 8. Зависимость напряжений в надувном куполе от приложенной в радиальном направлении растягивающей силы в двумерном случае

Отклонения точек отражающей поверхности от идеального параболоида после приложения давления (надува конструкции) приводятся на рис. 9. Отсюда видно, что даже при таких граничных условиях имеют место довольно серьезные смещения точек отражающей поверхности. СКО составляет 141 мм.

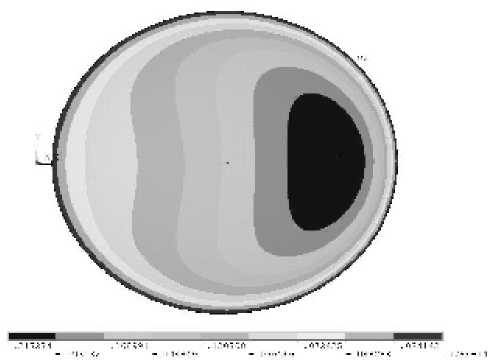
Рис. 9. Отклонения отражающей поверхности от идеального параболоида до регулировки ее начальной геометрии

Еще одной стороной масштабного фактора является рост напряжений в материале купола при увеличении размеров конструкции, что ведет к еще большей потере формы. Напряжения, возникающие в материале купола после приложения давления, показаны на рис. 10.

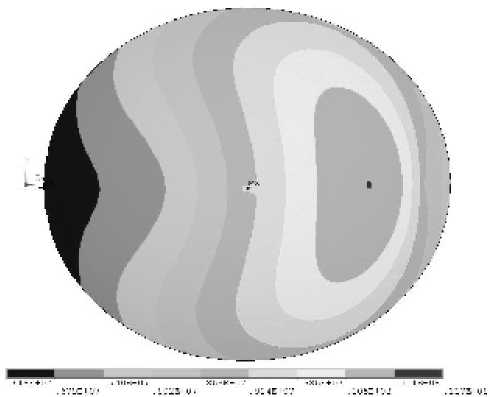
Рис. 10. Напряжения, возникающие в материале отражающей поверхности

Решение этих проблем осуществляется использованием в конструкции более жесткого надувного тора [4], фиксирующего купол с помощью растяжек и позволяющего корректировать форму отражающей поверхности, а также с помощью регулирования начальной формы отражающей поверхности рефлектора, т. е. изначально нам нужна поверхность с геометрией, несколько отличной от вырезки из родительского параболоида. Под регулировкой начальной формы подразумевается определение такой исходной геометрии отражающей поверхности, что при подаче газа в купол рефлектора мы получим рабочую поверхность с требуемыми радиотехническими характеристиками. После проведения регулировки СКО равно 3,5 мм, т. е. находится в области допустимых значений. Отклонения точек отражающей поверхности от идеального параболоида после регулировки отображены на рис. 11. Видно, что центральная область отражающей поверхности имеет отклонения порядка 1 мм, но ближе к краю купола картина ухудшается. Это связано с кривизной поверхности офсетного параболоида и проиллюстрировано на рис. 9. На нем хорошо видна область максимальных отклонений.

Данные о величине выполненной регулировки позволяют изготовить отражающую поверхность, которая будет удовлетворять всем радиотехническим требованиям.

Поместив отражающую поверхность в полесил тяжести и выполнив расчеты для двух положений «чаша вверх» и «чаша вниз» (см. рис. 12), мы выяснили, что разница положений ее точек между состоянием в невесомости и положениями «чаша вверх» и «чаша вниз» совпадает с точностью до третьего знака послезапятой. Расхождение составляет менее 2 %, что может быть объяснено кривизной поверхности.

В результате проведенных расчетов приходим к выводу, что хотя на отражающей поверхности и присутствуют области с достаточно большими отклонениями от идеального параболоида, но это не мешает нам добиться того, чтобы значение СКО находилось в требуемых пределах (порядка 3…5 мм).