Моделирование абразивных зерен с учетом их кристалломорфологических особенностей

Проблема получения однородных по размерам и морфометрическим характеристикам алмазных порошков в настоящее время все еще остается нерешенной. Это связано как с несовершенством технологических процессов получения таких порошков, так и с недостатками методического аппарата количественной оценки степени их однородности. С другой стороны, промышленность предъявляет все более жесткие требования к качеству порошков. Так, например, при изготовлении инструмента, применяемого для обработки внутренних поверхностей малого диаметра, требуются узко-классифицированные порошки, т.е. порошки одного размера и желательно изометричной формы, не содержащие крупных и мелких зерен.

Режущая способность шлифовальных инструментов, эффективность их применения, а также качество обработанных поверхностей во многом зависят от линейных размеров зерен. При моделировании процессов шлифования важным является использование формы абразивных зерен в качестве базовой модели.

В научной литературе имеются различные взгляды на выбор таких моделей. В работе [1] наиболее вероятной представляется форма зерна в виде конуса с закругленной вершиной, а также шара, в работах [2,3] – в виде эллипсоида вращения. Авторы исследования [4] описывают профиль зерна кривыми второго порядка. В работе [5] рассматривается форма алмазного зерна в виде цилиндра и куба. С учетом этих различий нами проведены сравнение различных моделей и регламентация их по степени приближения к экспериментальным данным.

В соответствии с законом кристаллографии, из всех возможных атомных сеток в кристаллической структуре габитусными становятся только те сетки, ретикулярная плотность которых в данном минерале наибольшая. Применительно к идеальной кристаллической решетке алмаза это означает, что его реальные кристаллы в качестве габитусной поверхности должны преимущественно иметь простую форму октаэдра [6].

Начало первой морфологической классификации якутских алмазов было положено Н.А. Бобковым, но преждевременная смерть в 1953 году не позволила ему завершить работу. М.А. Гневушев и З.В. Бартошинский , 1969 , основываясь на работах Н.А. Бобкова, выделили 10 кристалломорфологических типов алмаза, различающихся по форме кристаллов и геометрическому виду слоев роста на их поверхности (рис. 1):

При разработке классификации авторы использовали, главным образом, три основных кристалломорфологических типа алмаза: октаэдр, ромбододекаэдр и переходные между ними формы. Кристаллы кубической формы были добавлены позднее.

На примере алмаза хорошо видны отличия реальных кристаллов, образующихся в природных условиях, от идеальных образований, выводимых на основе теоретических представлений о строении кристаллической решетки [7]. Эти отличия обусловлены различными физико-химическими условиями роста алмазов в разных очагах кристаллизации. При этом кристаллы алмаза из одного месторождения могут иметь некоторые сходные морфологические признаки, позволяющие отличить их от кристаллов другого месторождения.

Все получаемые алмазы подвергаются дроблению с последующей классификацией по размерам на отдельные фракции. В зависимости от

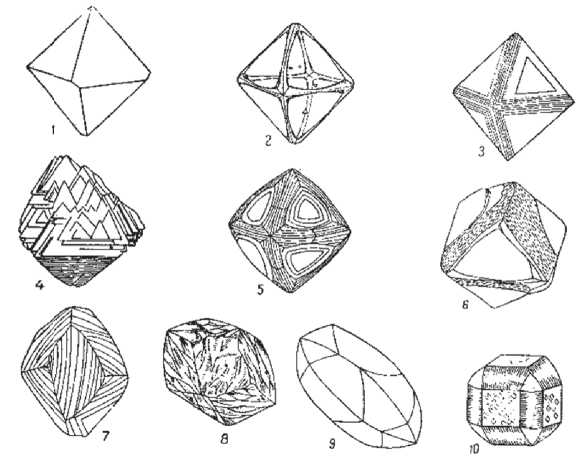
Рис. 1. Морфологические типы кристаллов якутских алмазов (по М.А. Гневушеву и З.В. Бартошинскому):

1 – плоскогранный острореберный октаэдр; 2 – плоскогранный октаэдр с притупленными ребрами;

3 – кристалл, сложенный уменьшающимися тригональными слоями роста; 4 – кристалл с полицентрически растущими гранями; 5 – кристалл, сложенный тонкими дитригональными слоями роста; 6 – кристалл с занозистой штриховкой; 7 – кристалл с округлоступенчатыми гранями; 8 - ромбододекаэдр с блоковой скульптурой; 9 – округлый кристалл удлиненной формы; 10 – кристалл кубического габитуса

размера зерна порошки условно делятся на три группы: шлифзерно, шлифпорошки и микропорошки [8,9].

Известно, что эффективность и высокое качество чистой обработки могут быть достигнуты только при использовании классифицирующих алмазных порошков, при максимальном содержании основной фракции [10,11].

В большинстве случаев частицы порошкообразных материалов имеет сложную направленную форму, для точного описания геометрии которой требуется большое число параметров, главной из которых, как правило, является размер частицы.

Целью работы выбор методов моделирования для определения базовой модели абразивных зерен, используемых в алмазных инструментах.

Объекты исследования : шлифпорошки природного алмаза, которые обладают повышенной износостойкостью и режущей способностью марки АС15: 50/40, 63/50, 80/63, 100/80, 125/100, 160/125, 200/160, 250/200, 315/250, 400/315, 500/400, 630/500 (мкм).

МЕТОДЫ ИССЛЕДОВАНИЯ

Размером зерна в алмазных порошках считается половина суммы длины и ширины проекции алмазного зерна на предметное стекло микроскопа или проектора. В соответствии с этим размеры зерен определяются по двум наибольшим по величине взаимно перпендику- лярным осям, которые могут быть условно проведены на площади проекции зерна (с учетом выступов). Размер большей оси принимается за длину, меньшей – за ширину зерна [12].

Рассев алмазов по размерам может производиться на любом вибрационном сите, обеспечивающем условия хорошего встряхивания и герметичности при небольших габаритах. Однако на ситах практически невозможно получить алмазные порошки, содержащие зерна только одного гранулометрического состава. Всегда присутствуют зерна других классов, меньших и больших размеров. Объясняется это несовершенством сит, а также тем, что зерна алмазов не имеют сферической формы, т.е. неизометричны.

Необходимые для моделирования процедуры контрольного ситового рассева размерные характеристики зерен определялись по двум проекциям, полученным с помощью растрового электронного микроскопа РЭМ XL-20 (Philips) в режиме вторичных электронов. Линейные размеры оценивали по трем взаимно перпендикулярным направлениям. За длину зерна принимался его наибольший размер, видимый на одной из двух проекций (рис.2). Измерение длины и ширины проекции зерен, их высоты, а также исследование морфологии алмазных зерен проводили по РЭМ–фотографиям.

В нашей оригинальной работе [7] предложены новые компьютерно-аналитические методы диагностики характеристик алмазных порошков, также передовая экстраполяционно-аффинная 3D модель зерна по-

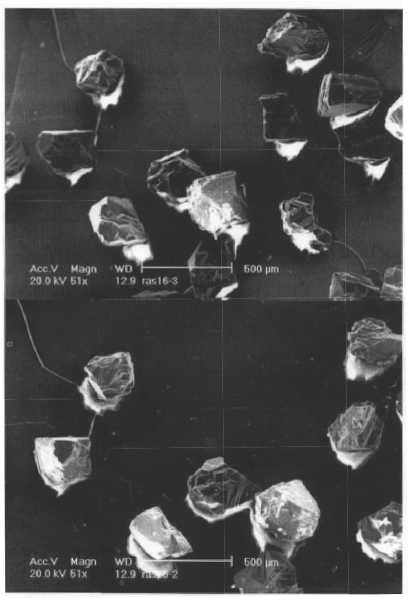
Рис. 2. Зерна шлифпорошка зернистости 315/250 природного алмаза в двух проекциях (РЭМ)

рошков сверхтвердых материалов (СТМ), которые были использованы для проведения расчетных данных, представленных в данной статье.

В качестве геометрической модели зерна абразивного наполнителя выбирался такой вариант модели, при котором критериальный параметр D , характеризующий величину отклонения объема реального зерна V_r от объема его модельного аналога V_m, принимает минимальное значение:

D =|l-[ £ ( V mi /V ri )²]^1/2/ P | , (1) i = 1

где i, P – порядковый номер и количество исследованных зерен, соответственно. Совокупность линейных измерений, необходимых для вычисления V_r и V_m , определяется формой АЗ.

Как известно, коэффициент формы Кф отдельного зерна определяется как отношение длины его проекции к ее ширине. Изометрич-ность зерен (в процентах), следуя методике стандарта [12], определяли по формуле u = u1 -100, (2) n где u1 – число изометричных зерен, n – число измеренных зерен. Число изометричных зерен u1 считали по результатам вычисления коэффициента формы. Изометричным считают зерно, коэффициент формы Кф которого не превышает 1,3. Полученные таким образом значения изо-метричности зерен исследовавшихся порошков показаны в таблице 1.

ЗАКЛЮЧЕНИЕ

Проведена диагностика шлифпорошков природного алмаза с учетом их кристалломорфологических особенностей. С помощью компьютерно-цифровой обработки были отобраны пробы по 300-350 зерен каждой разновидности исследованных алмазных шлифпорошков. Наиболее эффективно использование предложенной модели зерна в сочетании с современными компьютерно-техническими средствами автоматизированной диагностики [7] морфометрических характеристик абразивных порошков как инструмента получения исходных данных. Для выбора модели формы реального алмазного зерна необходимо наиболее точно определить линейные размеры зерна по объемным измерениям в двух проекциях. В качестве геометрической модели зерна природного алмаза рекомендуется брать эллипсоид (Табл.1) - по минимальному значению критериального параметра D , характеризующего величину отклонения объема реального зерна V_r от объема его модельного аналога V_m, абразивного наполнителя.

Результаты диагностики в одинаковой мере важны как для производителей порошков, так и для их потребителей. Для первых они нужны для идентификации порошка по тому или иному стандарту. Потребителям они важны для эффективного и рационального использования при изготовлении алмазно-абразивного инструмента и разработке алмазосодержащих композиционных материалов.

Таблица 1. Значения критериального параметра D для различных моделей зерен

Шлифпоро-шок (мкм)	Значения критериального параметра D для различных моделей зерен алмаза					Изометричность, %
ГОСТ	Прямоугольный параллелепипед	эллипсоид	сфероид	куб	октаэдр
50/40	0,161	0,071	0, 094	0,136	0,082	57,62
63/50	0,178	0, 081	0, 121	0,143	0,135	56,13
80/63	0,167	0,093	0, 137	0,162	0,114	52,14
100/80	0,189	0,114	0,172	0,172	0,134	49,12
125/100	0,183	0,127	0,163	0,191	0,154	55,66
160/125	0,212	0,179	0,239	0,156	0,167	54,31
200/160	0, 203	0,164	0,137	0,163	0,173	64,34
250/200	0,251	0,189	0,275	0,196	0,184	59,49
315/250	0,243	0,176	0,232	0,218	0,187	51,37
400/315	0,256	0,181	0,253	0,193	0,198	57,18
500/400	0,269	0,193	0,271	0,237	0,197	61,26
630/500	0,278	0,198	0,287	0,218	0,181	64,23