Моделирование аэрогидроупругости несущих поверхностей в авиатике мягких летательных аппаратов

The aviatics of soft flight apparatus is quite science–capacious field. Calculations by using Large–Particles Method permit to reduce the weight and price of parachutes. All types of modern and perspective parachutes (cosmic atmospheric re–entry, hypersonic, space shuttle drogue, round, conical, gliding–type, ribbon, with constructive holes etc.) are investigated by this method. The algorithm for solving of problem on stress–strain state in canopy is proposed. Canopy may be considered as pliable shell or measure. All practically important problems of aeroelasticity of parachute system (canopy opening; parachute braking with form changing; interaction of shoch waves and parachute, etc.) are investigated by this algorithm of Large–Particles Method..

В настоящее время активно развивается перспективная область машиноведения – авиатика мягких летательных аппаратов. К аппаратам данного класса относится огромный класс летающих устройств: парашюты, парапланы, баллюты, дельтапланы, аэростаты и др. Автором исследованы все эти летающие устройства, в том числе рассмотрены все типы парашютов: планирующие (однооболочковые и двухоболочковые), ленточные, тормозные, спасательные и др. Исследованы многокупольные системы. Особая сложность исследования парашютных систем заключается в том, что форма купола (и строп) не является неизменной, как в случае самолёта, дирижабля или спускаемого космического аппарата, а определяется в результате аэроупругого взаимодействия парашюта с окружающей средой.

Автором исследованы практически все задачи авиатики мягких летательных аппаратов: раскрытие купола парашютных систем, торможение парашюта с изменением его формы, взаимодействие ударных волн с парашютом и др. В аэродинамических расчётах им учтены упругость купола и строп (в том числе рассмотрены соответствующие разрушению предельные прочностные характеристики ткани купола и лент строп), вес парашюта и строп, реальный вес спасаемого объекта, внутреннее трение материала строп и купола.

С начала XX века центр проведения всех основных работ по теории и практике конструирования парашютов находится в нашей стране. Г.Е. Котельников в 1911 году изобрёл ранцевый парашют. В течение многих десятилетий основополагающими книгами по парашютостроению являлись монографии Н.А. Лобанова [1,2 и др.]. Значительный вклад в элементарную теорию парашютов внесли работы Х.А. Рахматулина [3,4 и др.]. Важные разделы, посвященные парашютостроению, содержатся в фундаментальных монографиях академика А.М. Матвеенко [5,6 и др.] и Генерального конструктора, академика Г.И. Северина [6 и др.].

Натурные и аэрофизические эксперименты дают небольшое количество информации, к тому же они экономически весьма дороги. Поэтому основным способом исследования парашютных систем в настоящее время является численное моделирование [7–18 и др.]. Наиболее мощным методом численного эксперимента, с помощью которого решены всевозможные задачи парашютостроения на всех режимах как дозвуковых, так и сверхзвуковых, является метод крупных частиц [19 и др.]. Единообразие вычислений этим методом позволяет впервые корректно поставить и решить многие комплексные практически важные задачи и достичь высокой точности получаемых результатов [20].

Опишем алгоритм метода крупных частиц для решения задачи о напряженно-деформированном состоянии купола парашюта. Купол рассматривается как мягкая оболочка (мембрана). В данной работе мы будем использовать традиционный подход теории упругости.

Для того чтобы показать, каким образом получаются соотношения метода крупных частиц применительно к расчету напряженно-деформированного состояния мягких оболочек, рассмотрим произвольную мягкую оболочку (рис. 1,а), с которой свяжем сопутствующую криволинейную систему координат a 1 , a ₂. Оболочка движется относительно внешней декартовой системы отсчета х 1 , х 2 , х 3 .

Дифференциальное уравнение движения мягкой оболочки в векторной форме запишем следующим образом:

Р o g o l u = /' [ ^{, Т} e' + T 2 e 2 )h 2 ] + d t da i

+       [ 6T 12 e i + T 22 e 2 )h i ] +А р g ,                       (1)

da 2

где р - масса единицы площади оболочки; верхний индекс "о" обозначает начальное (раскройное, недеформированное) состояние; g = 4g 11 g 22 - g 122 , h 1 = 4 ^ g 11 , h 2 = 4 У, g 22 — соответственно дискриминант метрического тензора поверхности и коэффициенты Ламе; g lm – компоненты метрического тензора ( l,m =1,2); u – вектор скорости оболочки; t – время; Т 11 , Т 12 , Т 22 – компоненты тензора мембранных усилий оболочки; e 1 , e 2 – единичные векторы локального базиса сопутствующей системы координат; А р – вектор поверхностной нагрузки. При анализе деформированного состояния мягких оболочек воспользуемся степенями удлинения

^ n = dsnldso = hnlh°o , n =1,2, или величинами относительных удлинений

£ n X n ¹

и углом сдвига

9 = Х о - X = Х о - arccos( g 12/ 4g 11 g 22 )•

Связь между мембранными усилиями и относительными удлинениями, и углом сдвига для изотропной оболочки можно записать в следующем виде:

EE

^T1 1 =--- i ^{( £} 1 ⁺ v ^£ 2 ) , T 22 =--- г ( £ 2 + v £ 1 ) , Т 12 = G 9 ,

1-v2                  1-v2

где Е - жёсткость материала оболочки при растяжении; G = E / [2(1+ v )] - жёсткость материала оболочки при сдвиге; v - коэффициент Пуассона.

Вычисленные по относительным удлинениям мембраны усилия должны удовлетворять условиям существования мягкой об олочки [20]:

T 11 ⁺ T 12 ⁺ 2 T 12 ^g 12 /4^g 11 ^g 22 >  ^{0 ;}

T 11 T 12 - 2 T 122 >  0.

Предположим, что нашей задачей является определение напряжённо-деформированного состояния мягкой оболочки при существенном изменении во времени её формы, т.е. координат х^=х^(а1,а2,t), ^=1, 2, 3, точек оболочки М(а1,а2), под действием заданных нагрузок с учётом связей, наложенных на оболочку. Знание координат х^ точек оболочки позволяет вычислить, как показано ниже, интересующие нас параметры – относительные удлинения и напряжения. Отметим, что задача расчёта мягкой оболочки при больших перемещениях является нелинейной, но применение при численных расчетах малых шагов по времени и пространству позволяет с приемлемой точностью линеаризовать исходную задачу. Рассмотрим способ получения разрешающих уравнений метода крупных частиц применительно к расчёту напряжённо-деформированного состояния мягкой каркасированной оболочки при больших перемещениях. Особенно просто получить соотношения метода крупных частиц для исследования динамики мягких оболочек, изготовленных из ткани. Координатные линии а1, а2 в этом случае целесообразно располагать вдоль основы и утка ткани, из которой изготовлена оболочка. Специфика работы таких оболочек проявляется в отсутствии сопротивления изгибу, сжатию и сдвигу. Исходное дифференциальное уравнение движения мягкой оболочки (1) без учета сдвиговых усилий в проекциях на оси координат х^ запишем в следующем виде:

Р o

д^ d (T i ) ^ д t да 1

д ( T 2 ) ^

⁺ —--- + А р ^ ,

да 2

где Т 1 , Т₂ - натяжения, действующие по направлениям координатных линий а 1 , а ₂; индекс ^ = 1, 2, 3 обозначает проекцию соответствующей величины на ось х ^ .

На оболочку наложим расчётную сетку (рис. 1,б). Узловым точкам присвоим номера i,j . Вспомогательной расчётной сеткой, сдвинутой относительно основной на полшага, разобьём оболочку на «крупные частицы». Сосредоточим массу каждой крупной частицы в соответствующей узловой точек i, j . Величину массы будем вычислять по формуле

M y = +р j (h i + i / 2 j + h ^ / 2 М + 1 / 2 + h*^ / 2 ) /4, где p j - масса единицы площади крупной частицы; h i,j ± _1/2 - расстояние между смежными узловыми точками.

Расчёт движения крупных частиц ведётся шагами по времени, каждый из которых содержит три этапа. На первом (эйлеровом) этапе определяют скорости движения крупных частиц. Разностное уравнение, аппроксимирующее уравнение (2), разрешённое относительно скорости U j в момент времени t^{k +1}= t^k + А t , запишем следующим образом:

(u kj ' % ⁼{( ^U k ) ^ ^{+ [ ( T} + 1 / 2 ,j - ^{T j} + 1 / 2 - T ij/ 2 ) ^ ⁺

⁺ (^ j ) £ ^{( h} i + 1 / 2 ,j ^{+ h} i- 1 / 2 ,j X^h ij + 1 / 2 ^{+ h} ij- 1 / 2 ) / 4 ] ( ^A t / ^Mij )] P , ⁽³⁾ где Т / ± 1 / ₂ , >T^k ± 1 / ₂ — погонные усилия в оболочке, А p ^k - усредненный перепад давления, действующий на крупную частицу и в общем случае являющийся функцией координат, времени, скорости движения оболочки и т.д., р - коэффициент демпфирования, гасящий нефизичные осцилляции (в случае их возникновения в процессе решения), связанные со способом аппроксимации континуальной задачи дискретным аналогом. Коэффициент в подбирается опытным путем и зависит от условий конкретной задачи. С целью устранения возможной немонотонности решения можно также пользоваться корректировкой скорости [21].

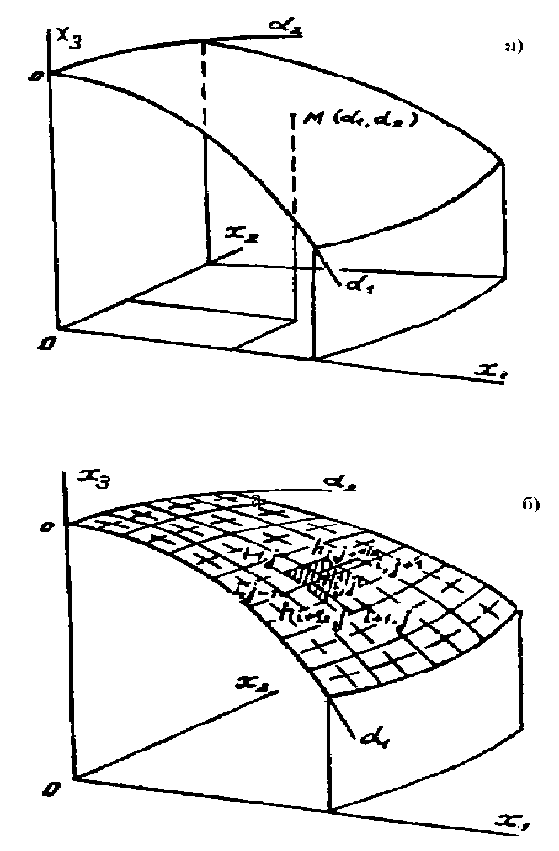
Рис. 1. Мягкая оболочка (а) и расчетная сетка, наложенная на оболочку (б) б

На втором (лагранжевом) этапе при использовании метода крупных частиц обычно вычисляются потоки массы через границы ячеек на временном слое t^{k +1}. В нашем случае принимаем, что обмен массами между крупными частицами не происходит ( Д М ^ = 0), а крупные частицы перемещаются в новое положение, характеризуемое координатами x k ^{+ 1} . Используя вычисленные на первом этапе скорости, находим эти координаты по формуле

( Х ^ ) j 1 = ( x ^ ) ¹ + U^ &  .

На заключительном этапе по полученным координатам вычисляем новые расстояния между крупными частицами (узловыми точками):

h k+1  — hi ±1 / 2,j =

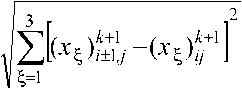
1 k + 1                   x k + 1    / x k + 11

h ij ± 1 / 2 =1 ^K x ^ ) i.j ± 1   ⁽ x ^ ) ij I .

V ^= 1

Зная новые расстояния между узловыми точками ячеек, определяем степени удлинения, возникающие в оболочке:

1 к + 1    — Z, k + 1 / L °

Л i±1 / 2j = hi±1 / 2 j hi ±1 / 2j , л к+1  7 k+1 /1 ° Л i.j±1 / 2 = hij±1 / 2/ hi.j±1 / 2 .

По степеням удлинения вычисляем натяжения в оболочке:

гр к + 1 _ т^к + 1   A k + 1

T i ± 1 / 2 ,j = E i ± 1 / 2 ,j ^(Л i ± 1 / 2 ,j k + 1        k + 1      k + 1

T i.j ± 1 / 2 = ^E i.j ± 1 / 2 ^(Л i.j ± 1 / 2

^{- 1 )} ,

^{- 1 )} ,

где Е i ± _1/2, , E_y ± 1/2 - приведенные жёсткости оболочки, зависящие от жёсткости материала оболочки и жёсткости каркаса, если последний проходит через данную крупную частицу. Приведенные жёсткости оболочки вычисляем по формуле:

⁺ h o - 1 / 2 ) / 2 ^] , ⁺ h o 1 ,j - 1 / 2 ) / 2 ^] , ⁺ h o 1 / 2 , ) / 2 ^] , ⁺ h ° - 1 / 2 .j-1 ) / 2 ^] ,

E k 1 / 2 ., = ( E 1 )^k + 1 / 2 , + ( E c )“ 2 , / K h °j + 1 / 2 F^{k + 1} -(FA^{k + 1} + (F ^{k + 1}   /1(/г °

^E i - 1 / 2 j = ^{( E} 1) i - 1 / 2 j ^{+ ( E} c ) i - 1 / 2 , ' H h M ,j + 1 / 2 ^{E k + 1}1 / 2 = ^{( E} 2) ^ / 2 ^{+ ( E} c ) ^ / 2 / K h io + 1 / 2 ,j ^Е ,1 / 2 = ^{( E} 2) ^k j\ / 2 ^{+ ( E} c ) , 1 / 2 / K h ° + 1 / 2 ,j- 1

где Е 1 , Е 2 - погонные жёсткости оболочки вдоль координатных линий a 1 , a ₂ , Е с -продольная жёсткость каркаса. Жёсткости оболочки и каркаса могут быть функциями степеней удлинения, скорости деформирования и зависят от вида напряжённо-деформированного состояния оболочки (одноосное, двухосное). В соответствии с особенностями работы мягких оболочек на вычисляемые натяжения накладываем условия:

k + 1 если Л i ± 1 / 2 .,

- 1 < 0 , то T^ j = 0 ,

^если k ki. +± 1 / 2 ^{- 1} <  0 , ^то T k +ti / 2 = ⁰ .

Погонные условия в материале оболочки и натяжения в каркасе подсчитываем по формулам:

k + 1            k + 1      k + 1

⁽ T 1 ) i ± 1 / 2 ,j = ^{( E} 1 ) i ± 1 / 2 ,j \^Л i ± 1 / 2 ,j ¹ ,

( T 2 ) j 1 / 2 = ( e 2 ) “ / 2 (л“ , 2 - 1 ) ,

( АГ A k +1   — ( k+ +1 f^ k +1 Й

( N1) i±1 /2,j = ( Ec )i±1 /2,j (Лi±1 /2,j 1), k+1           k+1     k+1

V ’2 iij ± 1 / 2 C^-'chj ± 1 /2\'„ч ± 1 / 2 .)■

При этом вычисляемые натяжения подчиняются условиям типа (5). Так как уравнения (3) – (4) реализуют явную конечно–разностную схему, то для устойчивости счёта интервал времени выбирается из условия устойчивости Куранта:

^ t <  h min V ^Pmin / ^E max ^.

Решение уравнений (3) – (4) осуществляется с использованием соответствующих начальных и граничных условий, выполняемых в узловых точках и зависящих от конкретной задачи. Стационарное решение получается в результате установления статического состояния.

В качестве тестового примера с помощью предложенного алгоритма метода крупных частиц была решена задача о раздувании эластичной прямоугольной мембраны, аналитическое решение которой для установившегося состояния известно. Рассматривалась первоначально плоская длинная прямоугольная мембрана, закреплённая вдоль длинных сторон, нагруженная равномерным перепадом давления. Результаты расчёта в безразмерном виде и сопоставление их с аналитическим решением даны на рис. 2 – рис. 4.

Приняты обозначения: х /а - безразмерная координата, R/а - радиус поперечного сечения деформированной мембраны; ж = A pa/E - параметр, связывающий перепад давления ∆ р, ширину первоначально плоской мембраны а и жёсткость материала мембраны Е; f/a - относительная стрелка прогиба мембраны; Т/Е - безразмерное натяжение мембраны. Численные значения исходных данных, принимавшиеся при расчёте мембраны, были следующими:

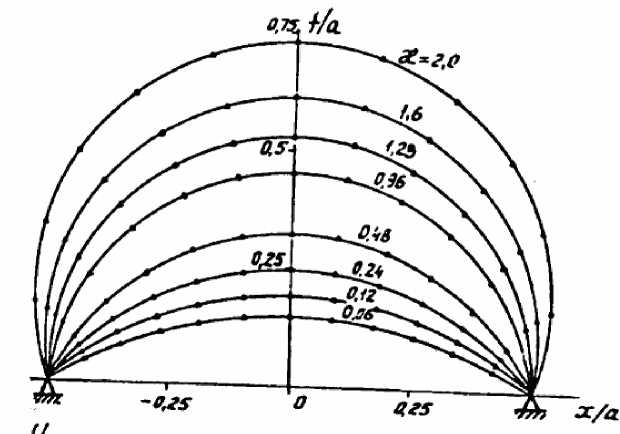
Рис. 2. Результаты решения задачи о раздувании эластичной прямоугольной мембраны

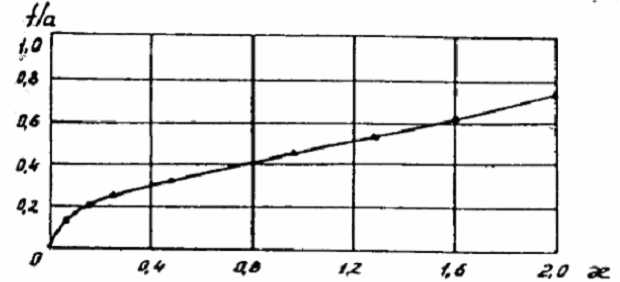
Рис. 3. Вычисленная величина относительной стрелки прогиба мембраны

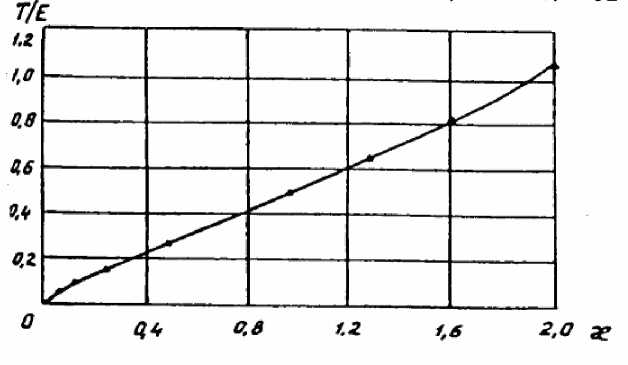
Рис. 4. Вычисленная величина безразмерного натяжения мембраны ширина мембраны а = 1,2 м, длина мембраны b = 6 м, перепад давления, действующий на мембрану, ∆р = 3,93 кПа, варьируемая жёсткость материала мембраны Е =2,35 … 78,5кН/м. В силу симметрии рассматривалась четвёртая часть мембраны, которая разбивалась на 36 крупных частиц. Связь между натяжениями и относительными удлинениями принималась подчиняющейся закону Гука. На рис. 2 представлены формы поперечного сечения мембраны в зависимости от параметра æ. Сплошной линией показаны результаты аналитического решения, треугольниками обозначены данные численного расчета.

Как видно из рис. 2, совпадение форм поперечного сечения мембраны, полученных аналитически и численно, наблюдается во всем диапазоне изменения параметра 0,06 ≤ æ ≤ 2. При этом относительные удлинения мембраны изменяются от 5 до 106%. На рис. 3 и в табл. 1 дано сопоставление безразмерной стрелки прогиба мембраны в зависимости от параметра æ при аналитическом и численном решениях. На рис. 4 и в табл. 2 приведено безразмерное натяжение мембраны в зависимости от того же параметра. В обоих случаях наблюдается вполне удовлетворительное совпадение аналитического и численного решений, что позволяет сделать вывод о хорошей сходимости численного расчета к точному решению данной нелинейной задачи.

Таблица 1.

Безразмерная стрелка прогиба мембраны при различных значениях æ

æ	Численный расчёт	Точное решение	Погрешность, %
0,06	0,1467	0,1458	0,6173
0,96	0,4583	0,4544	0,8492
2,0	0,7250	0,7253	-0,0414

Таблица 2.

Безразмерное натяжение мембраны при различных значениях æ

æ	Численный расчёт	Точное решение	Погрешность, %
0,06	0,05563	0,05581	0,3225
0,96	0,4860	0,4825	0,7254
2,0	1,058	1,070	1,075

Заметим, что реальная ткань является неизотропной оболочкой. Она неодинаково растягивается (и садится) в разных направлениях. Это связано с технологией производства тканых материалов. В процессе тканья нити уткá переплетаются с нитями основы. Нити уткá проходят через ткань с меньшей волнистостью, чем нити основы. Нити основы получают бóльшую волнистость, и поэтому по основе ткань тянется больше, чем по уткý. В табл. 3 приведены полученные экспериментально показатели сопротивления ткани растяжению.

Показатели сопротивления ткани растяжению

Таблица 3.

Продолжительность испытаний (час)	Расстояние по основе (м)	Расстояние по уткý (м)	Расстояние по диагонали (м)
0,5	9	7,5	24
6	9	7,5	24
24	10,5	7,85	24,25
12009	12	9,0	25

При кратковременных полётах парашютов указанные неравномерности растяжения не имеют практического значения. В случае же долговременно работающих тормозных устройств (типа плавучих якорей и др.) может существенно исказиться форма первоначального раскроя.