Моделирование акустических сигналов при оптоакустическом преобразовании для осесимметричных несферических форм эритроцитов

При воздействии короткого лазерного импульса на тканевую жидкую среду происходит поглощение света, и в результате термоупругого расширения излучается импульс акустического давления, который можно зарегистрировать ультразвуковым преобразователем. Форма и длительность акустического сигнала может говорить о форме и количестве объектов в жидкости, участвующих в поглощении лазерного импульса в биожидкости. В работах [1–11] проводились расчеты сформированного акустического сигнала в результате оптоакустического преобразования для математических моделей неагрегированных и агрегированных эритроцитов, в том числе с учетом кислородона-сыщения. В этих исследованиях для упрощения использовалась сферическая модель формы эритроцита. В настоящей работе приведена математическая модель патологических форм эритроцитов для исследования изменения форм эритроцитов с помощью оптоакустического метода.

Структурная организация мембраны эритроцитов человека позволяет ей претерпевать большие обратимые деформации, сохраняя при этом свою структурную целостность в течение 4-месячного пребывания в кровообращении. Мембрана обладает высокой эластичностью, быстро реагирует на приложенные гидравлические напряжения. В то время как нормальные эритроциты могут деформироваться с линейным расширением примерно до 250 %, увеличение площади поверхности на 3–4 % приводит к лизису клеток. Следовательно, важной особенностью индуцированных деформаций эритроцитов как in vitro , так и in vivo является то, что они не вызывают значительного изменения площади поверхности мембраны [12].

Снижение отношения площади поверхности клеток к объему и, как следствие, увеличение сферичности клеток является отличительной чертой эритроцитов при наследственных сфероцитозе (HS), эллиптоцитозе (HE) и гипергидратирован-ном стоматоцитозе (OHS). В случае HS и HE повышенная сферичность является результатом потери площади поверхности ячейки, в то время как в случае OHS она является результатом увеличенного объема ячейки.

HS является распространенной наследственной гемолитической анемией, поражающей все этнические группы, но особенно распространена у людей североевропейского происхождения (1 на 3000 человек). HS обычно ассоциируется с доминантным наследованием (75 %), хотя случаи, когда наследование не является доминантным (25 %), — не редкость. Типичная HS характеризуется наличием гемолиза с анемией, желтухой, желчными камнями и наличием сфероцитов на мазках периферической крови. Тем не менее клинические проявления HS варьируются от легкой до очень тяжелой анемии. Общей чертой всех форм HS является потеря площади поверхности мембраны и результирующее изменение формы клеток от дискоцитов к стоматоцитам, к сфероцитам. Поскольку эритроциты с уменьшенной площадью поверхности мембраны не могут эффективно пройти через селезенку, они изолируются и удаляются из кровотока селезенкой. Важно отметить, что тяжесть анемии связана со степенью уменьшения площади поверхности мембраны [12].

Рис. 1. Геометрия формирования акустического сигнала при оптоакустическом преобразовании

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Оптоакустический эффект описывается уравнением [13, с. 282], [14], которое можно записать через потенциал скорости ϕ как:

(

V ²

I

—

1 д_) с2 б t2J

ф =

β ρC p

^Ht ^,

Рассмотрим геометрию нерегулярного поглотителя лазерного излучения в жидкости с азимутальной симметрией. Запишем в сферических полярных координатах ( r ' , 0 ', ф ') с помощью замены r' = F ( S '); F ( S' ) — функция, связывающая r' и 0 (рис. 1).

Используем сферические гармоники для параметризации морфологии клеток [16, 17]. Этот набор функций может соответствовать как симметричным, так и несимметричным объектам. В этом случае контур ячейки можно разложить по полиномам Лежандра

r ' ( 0 ' ) = R e

где c — скорость звука, ρ — плотность жидкости, β — коэффициент расширения изобарического объема, C p — удельная теплоемкость, t — время и H t — функция нагрева, определяемая как тепловая энергия, внесенная оптическим лучом; p = — р б ф / 9 t .

Если оптическое излучение с интенсивностью I ₀ распространяется вдоль оси X и изменяется со временем синусоидально, то функция нагрева может быть выражена как Ht( x , t ) = μI 0 e ^{– ωt} . Здесь μ — коэффициент оптического поглощения освещенной среды. Для такой функции нагрева поле звукового давления в установившемся режиме сводится к выражению [15]:

V

к

—

-1 - 1 v 2 д ² J

ф=<

\а>в0 о (внутри поглотителя),

0 (снаружи поглотителя).

¹ + ^ ^a n ^P n ⁽ cos S ')

n

где R e — радиус сферической оболочки, охватывающей эритроцит; α n — параметр, описывающий форму; P n — многочлен Лежандра степени n . Любая произвольная функция между 0 <  0' <  п может быть выражена через базисные векторы. Используем это условие для получения нормальной формы дискоцита. Двумерное поперечное сечение фигуры и трехмерная фигура приведены на рис. 2.

Расстояние r'(0') точки на поверхности для сфероидальной частицы запишем в виде:

r-(0-) =

ab

[ b² sin² 0' + a² cos² 0 ' ]

где a и b — полуоси.

На рис. 3, 4 приведены сфероиды с различными пропорциями, причем у всех частиц объем неизменный. Уравнения для несферического объекта имеют вид:

а

–1

–2

–3

–4

–1

–2

–3

–4

–4

б

–4

–5–5

–4  –3  –2

–1    0    1

x ,

2 мкм

Рис. 2. Моделируемая форма здорового эритроцита. а — изометрия, б — поперечное сечение

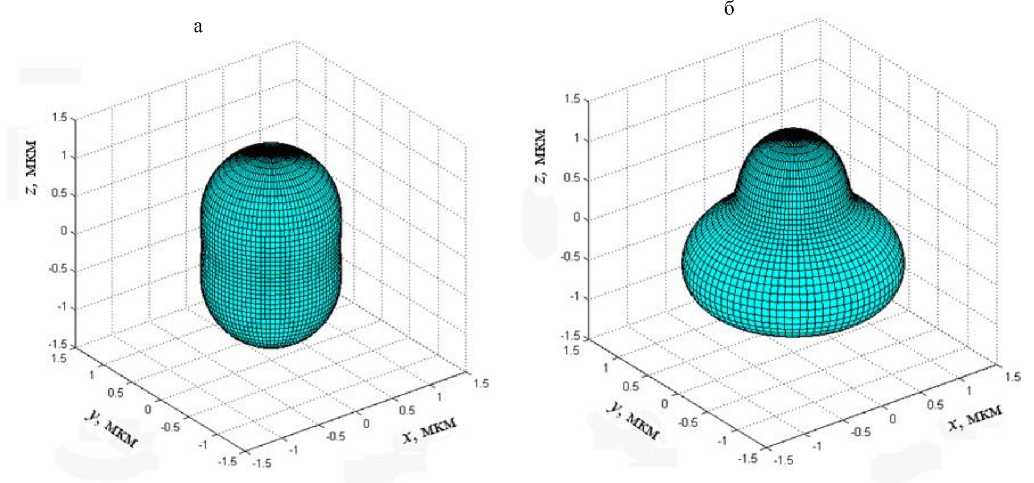
Рис. 3. Частицы, построенные с помощью многочлена Чебышева с ε = 0.25. а — n = 2, б — n = 3

^{i kr}       π                F ( θ )          2 π

p ( r , k ) =-— А Sin OdO f    r o ²d r ,J e- k W (5)

4 πr ^{0           0          0}

Расчет интеграла проводится численным методом с использованием полинома Чебышева для различных сферических и осесимметричных несферических частиц, поглощающих лазерное излучение и формирующих акустическое поле.

МОДЕЛИРОВАНИЕ

Для построения фигуры с помощью многочлена Чебышева расстояние от точки на поверхности можно записать в виде [18]:

r'O) = R c [ 1 + £ T „ (cos O ') ] ,             (6)

где T _B (cos O ') = cos n O' — многочлен Чебышева

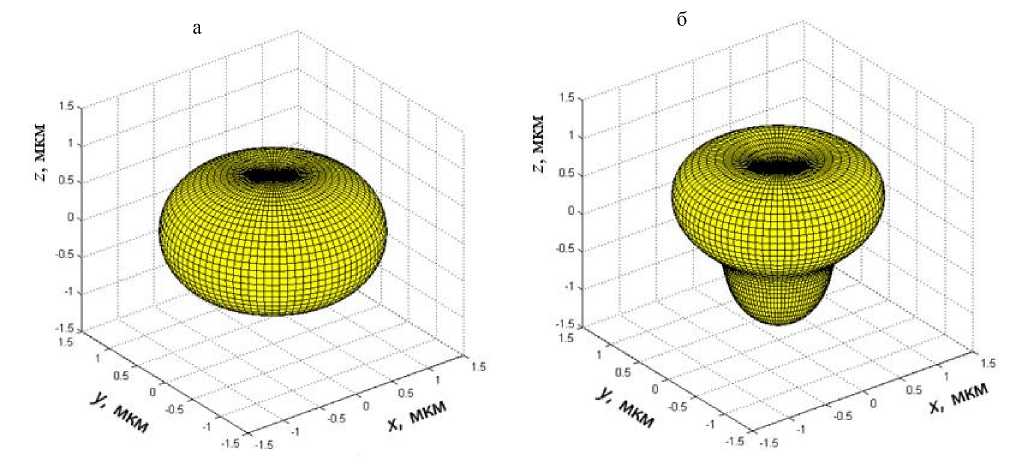
Рис. 4. Частицы, построенные с помощью многочлена Чебышева с ε = –0.25. а — n =2, б — n =3

степени n , где n определяет параметр волнистости, R c — радиус невозмущенной сферы, а ε — параметр деформации.

Частица формируется непрерывным деформированием сферы с использованием многочлена Чебышева степени n .

Частицы с фиксированным объемом приведены на рис. 3 для ε = 0.25 и рис. 4 для ε = –0.25. При четном значении n частицы симметричны относительно плоскости, перпендикулярной оси симметрии. Значения пиков, прогибов (кривизны поверхности) возрастают по мере увеличения величины ε.

Зрелая клетка имеет ширину около 7.8 мкм и толщину 1.7 мкм. Двояковогнутая форма (рис. 2) обеспечивает максимальную гибкость, а форма колокола используется для прохождения самых маленьких капилляров, которые имеют диаметр всего 5 мкм. Способность эритроцитов восстанавливаться после повторяющихся напряжений турбулентной циркуляции зависит от конструкции мембраны.

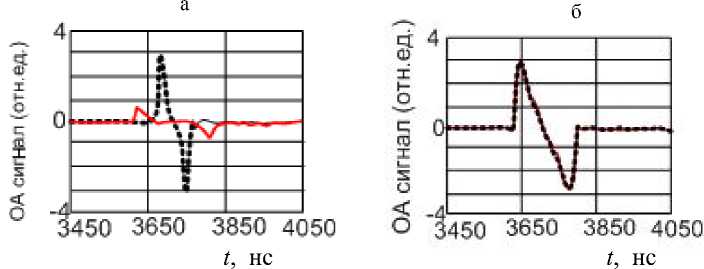
Рис. 5. Моделируемый акустический сигнал, формируемый дискоци-том и патологически измененным эритроцитом при оптоакустическом преобразовании (ОА).

Приведены сигналы в направлениях θ = 0 (пунктир) и θ = π/2 (сплошная линия) на ось симметрии: (a) дискоцит; (б) сфера

На рис. 5 приведен рассчитанный акустический сигнал, формируемый в результате оптоакустического преобразования в жидкости от дискоцитов и сфероидальных моделей эритроцитов с одинаковым объемом. В моделировании использовались параметры лазерной установки LIMO 100-532/1064U [1, 8–10]. Моделирование проводилось в среде Matlab 2017.

ЗАКЛЮЧЕНИЕ

Для определения формы эритроцитов с помощью оптоакустического эффекта была разработана двухмерная модель изменения формы эритроцитов для моделирования акустического сигнала.

Рассчитанные акустические сигналы отличаются для разных частиц в зависимости от их ориентации. Акустический импульс рассчитан, когда приемник расположен при θ = 0, как показано на рис. 5, а. Амплитуда сигнала уменьшается в четыре раза, а длительность акустического сигнала в три раза увеличивается при зондировании в направлении θ = π/2. Для однородной сферы сигналы идентичны со всех сторон (рис. 5, б). Моделирование параметрической поверхности является активной областью исследований в анализе медицинских изображений [16–20]. Поэтому сложные формы могут быть смоделированы с использованием сферических гармонических функций. Можно также предположить, что акустические сигналы от клеток и органелл могут быть получены через сферические гармонические функции для количественной оценки их морфологий.