Моделирование алгоритма вычисления граничного ранга матрицы на основе построения двудольного графа в среде MATLAB

Граничным рангом двоичной матрицы называется минимальное число строк и столбцов, в которых содержатся все ненулевые элементы матрицы. Проблема, вычисления граничного ранга, матрицы имеет важную роль в оценке характеристики кодов в гранично-ранговой метрике [1].

Алгоритм вычисления граничного ранга, матрицы на. основе сравнения между векторами был предложен автором в работе [2]. Метод вычисления граничного ранга, матрицы на. основе построения двудольного графа, был введен Ю. А. Альпиным и С.Н. Ильиным в 2006 году. В данной работе автор предложит моделировать этот алгоритм в среде Matlab. По сравнению с алгоритмом в работе [2], предложенный метод имеет меньшую временную сложность.

Пусть граничный ранг ДА) = 2 и предположим, что матрица A:

(0		0	1	0	0
	0	0	0	0	0
A=	0	0	1	0	0
	1	1	1	0	1
\ 0		0	0	0	0

Сразу видно, что искаженные символы сосредоточены в третьем столбце и четвертой строке.

• 2.    Описание алгоритма

Рассматривается теорема Кёнига, описывающая эквивалентность между задачами вычисления граничного ранга матрицы и нахождения максимального соответствия.

Теорема 1. ( Теорема Кёнига) В любом двудольном графе число рёбер в максимальном соответствии равно числу вершин в наименьшем вершинном покрытии.

Иными словами: Если прямоугольная матрица составлена из нулей и единиц, то минимальное число линий (строк и столбцов), содерэюагцих все единицы, равно максимальному числу единиц, которые могут быть выбраны так, чтобы никакие две из них не лемсали на одной и той мсе линии.

Теорема Кёнига была доказана Денешем Кёнигом в 1931 году [4].

Алгоритм максимальных соответствий в двудольных графах был введен Дж.Э. Хопкрофтом и Р. М. Карпом в 1973 году. Более подробно об этом алгоритме читатель может прочитать в статье [5]. Мы просто вспоминаем о результатах, необходимых в этой работе.

Соответствие и увеличивающий путь. Пусть G = (V, Е) - конечный неориентированный граф (без петель, множественных ребер или изолированных вершин), имеющий множество вершин V и множество ребер Е. Ребро, соединяющее вершины v и w, записывается {v,w}. Множество М СЕ является соответствием. если никакие вершины v EV не падают с более чем одним ребром в М. Соответствие максимальной мощности называется максимальным соответствием.

Вершина v является свободной, если она падает без ребра, в М.

Путь (без повторяющихся вершин)

Р = ( vi, V2 ) , ( V2, V3 ) , . . . , (V2k-1, V2k )

называется увеличивающим путем, если его конечные точки v1 и v₂k оба свободны, а его ребра попеременно находятся в Е — М и в М; т.е.,

Р ^М = { ( V2,V3 ) , ( V4, V5 ) , ( V6, V7 ) , . . . , (v2k-2,V2k-1)Y

• 2.1.    Построение двудольного графа

Двудольный граф - это граф, вершины которого можно разделить на. два. независимых множества. R и S. так что каждое ребро (r,s) либо соединяет вершину 11:3 R в S. либо вершину из S в R. Можно также сказать, что не существует ребра, соединяющего вершины одного и того же множества.

Граничный ранг матрицы A размером т хп может быть найден путём решения задачи поиска, максимального соответствия в двудольном графе (рис. 1). Вершины двудольного графа являются, с одной стороны, строками A, а с другой - столбцами A.

	т + 1 т + 2  ... т + п
1 2 A = • •	/  «1,1        «1,2      . . .      «1,п  \ «2,1        «2,2      . . .      «2,п •                                •                      •                             • •                                •                         •                          •
• т	•                                •                             •                      • \ « т, 1     « т, 2    . . .     « т,п '

и столбец   12

Ребро соединяет строку 11

тогда и только тогда, когда

«₂₁,22 = 0,1 <  11 <  т, т + 1 <  12 <  т + п.

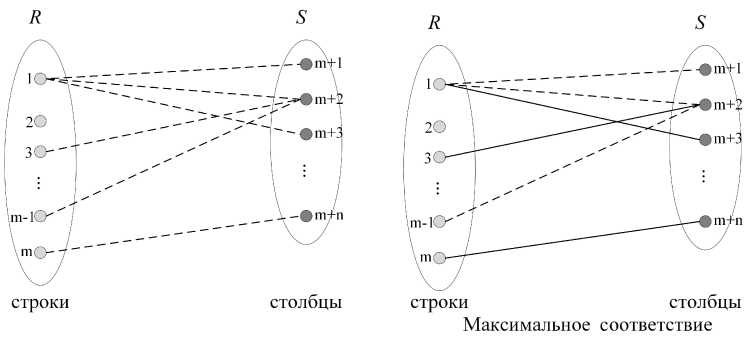
Рис. 1. Пример двудольного графа

Соответствие в двудольном графе - это набор ребер, выбранных таким образом, чтобы ни одно из двух ребер не имело общей конечной точки. Максимальное соответствие - это соответствие максимального размера (максимального количества ребер). В максимальном соответствии, если к нему добавляется какое-либо ребро, оно больше не является соответствием. Для данного двудольного графа может быть несколько максимальных соответствий.

Задача Максимального Двудольного Соответствия (МДС) может быть решена путем преобразования ее в потоковую сеть. Мы покажем, как эффективно выполнить такое задание, используя алгоритмы Форда и Фулкерсона [6]. Ниже приведены следующие шаги.

• 2.2.    Алгоритм Форда-Фулкерсона для задачи максимального потока

Алгоритм Форда-Фулкерсона, вычисляющий максимальный поток в потоковой сети, был введен Фордом и Фулкерсоном [6]. Идея, лежащая в основе алгоритма, проста. Пока существует путь от источника (начальный узел) до стока (конечный узел) с доступной мощностью на всех ребрах пути, поток будет отправляться по одному из этих путей. Тогда будет найден другой путь и так далее. Путь с доступной мощностью называется увеличивающим путем (an augmenting patKy Увеличивающий путь - это путь (и1 ,и₂, ..., и^ ) в остаточной сети, где к = 4, и1 - источник, и₂ = щ G Я, и₃ = s₂ G S и₄ - сток.

• 1)    Построение потоковой сети.

В потоковой сети должны быть источник и сток (рис. 2). Источник добавляется, а ребра добавляются из источника во все строки. Аналогично, ребра добавляются из всех столбцов в сток. Мощность каждого ребра обозначается как 1 (единица).

• 2)    Поиск максимального потока.

Алгоритм Форда-Фулкерсона используется для нахождения максимального потока в потоковой сети, построенной на шаге 1 (рис. 3). Максимальный поток - это значение, которое нужно найти (см. алгоритм 1).

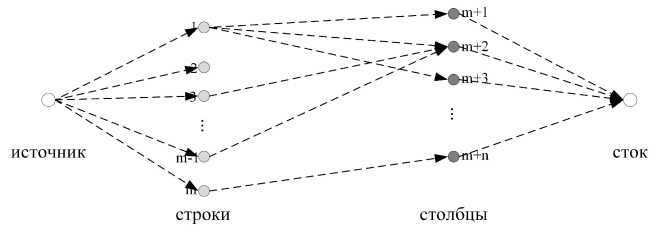
Рис. 2. Построение потоковой сети

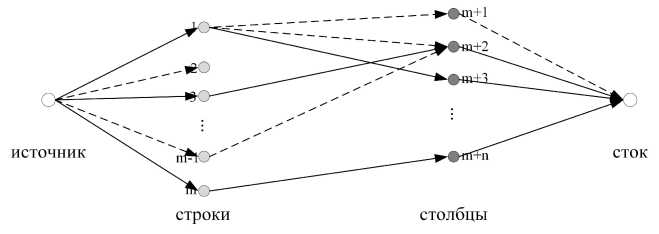
Рис. 3. Поиск максимального потока в потоковой сети

Алгоритм вычисления граничного ранга матрицы на основе построения двудольного графа выглядит следующим образом (см. алгоритм 2).

Преимуществом этого метода по сравнению с методом определения граничного ранга матрицы, основанным на сравнении между векторами, является сравнительно низкая временная сложность. Кроме того, этот метод может быть выполнен в параллельном режиме при примерно больших размерах матриц.

Недостаток этого метода - эффект параллельных процессов возникает только в параллельном алгоритме Форда-Фулкерсона, а не в оригинальном алгоритме.

Сложность вычисления граничного ранга матрицы на основе алгоритма Форда-Фулкерсона составляет О((п + т)п² ).

• 2.3.    Пример

Рассматривается матрица E размером 4 х 5 над GF (2)

1 ⎛1  0 0 0 0⎞

201000 E=

3 ⎝1  0  1   1   1⎠

Algorithm 1 Алгоритм Форда-Фулкерсона (граф G, источник s, сток t)

• 1:    Initialize flow to 0

• 2:    path = FIND_AUGMENTING_PATH(G, s,t)

• 3:    while path exists do

• 4:    augment flow along path

• 5:    G _f = CREATE_RESIDUAL_GRAPH()

• 6:    path = FIND_AUGMENTING_PATH(G_/, s, t)

• 7:    return flow

Algorithm 2 Calculate term rank of matrices

• 1:    procedure Calculate term rank

Input: A is matrix

Output: Term rank (matrix A)

• 2:    Quick check if A is matrix

• 3:    (m, n) — size of matrix A               >  m and n are numbers of rows and columns

• 4:      if A^j = 0 then A-ц = 1, Vi, j : i = 1,..., m; j = 1,..., n

• 5:     matchR a vector of length n                        > Initially all columns are available

• 6:     for Z = 1 to П do

• 7:        matchR(i) — 0

• 8:      result — 0                                                            > Initialize flow to 0

• 9:     for r = 1 to m do

• 10:         seen a vector of length n             > Mark all rows as not seem for next columns

• 11:         for i = 1 to n do

• 12:            seen(i) — 0

• 13:        path = bpm(A, r, seen, matchR)

• 14:        if path then                              > Find if the row ’r’ can match a column

• 15:           result — result + 1                       > Count of rows assigned to columns

• 16:     return result                                      > Return maximum matching

• 3.    Моделирование алгоритма в среде MATLAB

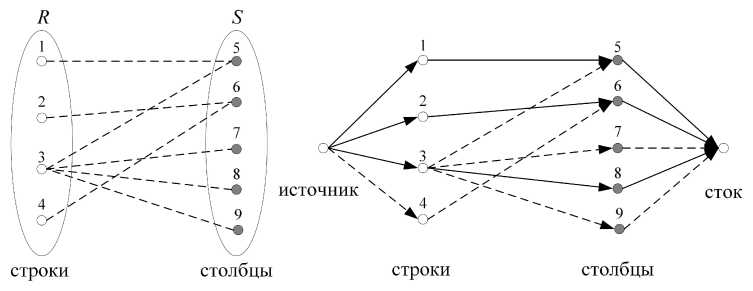
Рис. 4. Пример вычисления граничного ранга с помощью алгоритма Форда-Фулкерсона в потоковой сети

Рис. 4 иллюстрирует пример построения соответствий в двудольном графе и поиска максимального потока в потоковой сети. Видно, что максимальный поток равен 3. Так как граничный ранг р(Е) = 3.

Код Matlab, maxBPM.m, для алгоритма вычисления граничного ранга матрицы на основе построения двудольного графа

% Program code Matlab to find

% Maximum Bipartite Matching function у = maxBPM(A)

if ~ ismat rix (A)

error ( ’ Input _must-be_a_matrix ’) end

• %    M is number of rows

• %    and N is number of columns

[M,N] = size (А) ;

% Initially all columns а те available matchR = zeros (1,N);

matchR (:)= — 1:

% count of tows assigned to columns result = 0;

for u=lM

• %    Mark all tows as not seem for next columns seen = zeros(1 , N) ;

seen(:) = 0;

• %    Find if the row ’u ’ can match a column

[z , matchR] = bpm (A, u, seen , matchR);

if Ы result = result +1;

end end

% Return maximum matching у = result;

return end

Код Matlab, bpm.m, для алгоритма Форда-Фулкерсона

function [z , matchR] = bpm(A , u, seen, [M,N] = size (A) ;	matchR)
% Try every column one by one for v=l:N if (A(u,v) && (~seen(v))) % mark columns ’v ’ visited seen(v)= 1; if ( (matchR] v) <0) ) matchR (v)=u; z = 1; return end
[z , matchR] = bpm (A, matchR] if Ы matchR (v)=u; z = 1; return end end end z = 0; return end	v) , seen ,	matchR) ;

Например

» А = [1 1 0 1 0; 1 1 0 1 0; 0 1 0 1 0; 1 0 0 0 0];

» шахВРМ(А)

ans = 3

Используя алгоритм, граничный ранг матрицы A равен 3.

• 4.    Сравнение и оценка двух алгоритмов

  Алгоритм 1 был предложен автором в 2018 г. [2]. Алгоритм 2 представлен в данной работе. Здесь два алгоритма вычисления граничного ранга матрицы сравнены и оценены по нескольким важным критериям:

• 1)    Аппаратное требование вычислительная реализация

Количество переменных с их размером должно быть использовано в алгоритме 2, больше, чем в алгоритме 1. Кроме того, алгоритм 2 использует подфункцию в каждом цикле, поэтому требования к аппаратному требованию алгоритма 2 больше.

• 2)    Временная сложность алгоритма

Согласно приведенному выше анализу, сложность алгоритма 1 равна О(п4), а алгоритм 2 со сложностью - О(п3). Очевидно, что алгоритм 2 имеет меньшую сложность, чем алгоритм 1.

• 3)    Возможность работы в параллельном режиме с большим размером матриц

• 5.    Приложение для оценки характеристики гранично-ранговых кодов

Оба алгоритма могут быть реализованы в параллельном режиме, но алгоритм 2 должен использовать особенный алгоритм для этого режима.

Из приведенных выше результатов сравнения можно сделать вывод, что оба алгоритма практически эквивалентны по критериям оценки. Однако сегодня при большом объеме оперативной памяти алгоритм 2 приносит больше эффективности.

Порождающая матрица кода [5 х 7, 3 • 7, 3] с гранично-ранговым расстоянием 3 в столбцевом представлении имеет вид [7]:

С 3,Column = [ h 0 h l h 2 Ғ 7 Һ 0 + F 7 h i + F 7 h 2 F 7h) + F ^ h l + F ^ h 2] .       (1)

Здесь h o, h i, Һ 2 - информационные вектор-*-голбцы длины 7. а матрица F 7 - сопровож-

дающая матрица многочлена /(ж) =		ж7 +	/бЖ6	+ /5Ж5		+ /4Ж4 + /3Ж3 + /2Ж2 + /1Ж + /о
	" 0	1	0	0	0	0	0"
	0	0	1	0	0	0	0
	0	0	0	1	0	0	0
F 7 =	0	0	0	0	1	0	0
	0	0	0	0	0	1	0
	0	0	0	0	0	0	1
	. /о	/1	/2	/з	/4	/5	/6.

Например, матрица F7 выбирается как сопровождающая матрица многочлена ж⁷ + 1.

Из табл. 1 получено гранично-ранговое расстояние d ( C i — C j ) > 3. Таким образом, выбранная матрица F7 много члена ж⁷ + 1 удовлетворяет требованию кода.

Таблица!

Результат вычисления граничных рангов всех кодовых матриц С з ,соінтп

Граничный ранг С з ,соіитп	0	1	2	3	4	5
Количество матриц	1	0	0	1677	91524	2003950

• 6.    Заключение

Метод вычисления граничного ранга матрицы на основе построения двудольного графа рассмотрен. Сложность этого алгоритма составляет O(n3). С помощью этого алгоритма решалась задача оценки характеристики кодов в гранично-ранговой метрике.