Моделирование алиасинга в ПЗС-формирователе сигналов изображений

Введение1

За последние четыре десятилетия твердотельные формирователи сигналов изображений (ФСИ) на базе ПЗС [1] существенно вытеснили вакуумные приемные электронно-лучевые трубки из телевидения, вошли составной частью в компьютеры [2], мобильные телефоны, планшеты, разнообразные камеры цифрового фотографирования и видеонаблюдения [3]. Они революционизировали современные научные приборы, в особенности космические средства цифрового видеонаблюдения [4; 5] и астрофизических исследований [6].

Постоянно возрастают их разрешающая способность и чувствительность, расширяются спектральные диапазоны [7]. Однако при освое-

ВЕСТНИК 2017

нии новых спектральных диапазонов часто проявляют себя физические пределы, препятствующие уменьшению размера А чувствительного элемента (пикселя). Большой размер пикселя ограничивает разрешающую способность преобразователя [8], в чем также повинен и алиасинг [9]. Статья отражает результаты компьютерного моделирования твердотельного формирователя сигналов изображений, дающие оценки для максимального, минимального и среднего значений функции передачи контраста и уровня шумов, вызванных алиасингом и зависящих от пространственной частоты v . Моделирование позволяет оценивать различные подходы к сверхразрешению матриц ПЗС [10].

1.    Алиасинг в дискретных формирователях сигналов изображения

Алиасинг при формировании сигналов изображений - это нерегулярность сигнала, вызванная интерференцией изображения с дискретной структурой преобразователя.

На ранних стадиях развития радиоэлектроники было обращено внимание на алиасинг при аналого-цифровом преобразовании периодически модулированных сигналов преобразователем с частотой дискретизации сигнала, близкой к частоте модуляции входного сигнала. В аналоговом телевидении алиасинг проявился как результат интерференции (биений) пространствен-но-модулированного изображения с дискретной структурой развертки. Его можно было видеть при преобразовании тестовой телевизионной таблицы с расстоянием между штрихами, близким к расстоянию между линиями горизонтальной развертки.

В матричных преобразователях изображений любого типа - видимого или инфракрасного диапазонов, тепловых, ультрафиолетовых, рентгеновских или микроволновых - преобразованный сигнал меняется со сдвигом изображения относительно дискретной структуры преобразователя. С расширением внедрения твердотельных формирователей сигналов изображений на основе приборов с зарядовой связью (ПЗС) или матриц с комплементарной структурой металл-окисел-полупроводник (КМОП) возрастает значение проблемы алиасинга, который проявляется в результате фазовых сдвигов элементов изображения относительно дискретной структуры преобразователя.

Разнообразные матричные преобразователи, работающие в диапазонах спектра за пределами видимого диапазона, в результате физических или технологических ограничений не могут иметь малый размер пикселя и испытывают за- метное влияние алиасинга. При наличии технологических ограничений на минимальный размер пикселя А проблема алиасинга становится весьма серьезной и требует мер по снижению искажений преобразованного сигнала, вызванных алиасингом.

При малом размере А чувствительного элемента преобразователя (пикселя) относительно мельчайших деталей изображения эффект алиасинга несуществен. Минимальный размер пикселя в преобразователях видимого диапазона сегодня достиг четырех микрометров. Оптическая система, формирующая изображение на поверхности матричного преобразователя, в этом случае действует как пространственный фильтр низких частот. По теореме В .А. Котельникова [11], преобразование сигнала с ограниченным спектром-преобразователем с частотой дискретизации, превышающей в два и более раз максимальную частоту исходного сигнала, происходит с абсолютной точностью, которая не зависит от фазовых сдвигов исходного сигнала относительно последовательности выборок.

Представление об алиасинге можно получить, сравнивая распределения зарядов в ПЗС Z ( n ), получаемые при преобразовании изображений точечного объекта при различных его фазах относительно структуры матрицы (рис. 1).

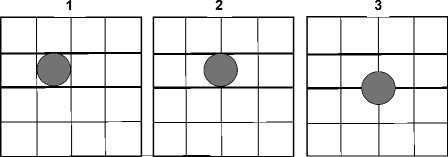
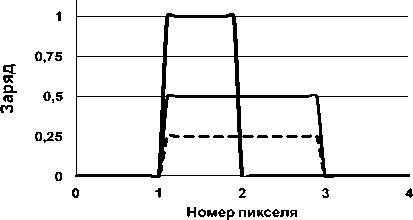
Рис. 1. Варианты изображения точечного объекта при различных фазах сдвига изображения относительно дискретной структуры матрицы ПЗС:

1 - центр точечного изображения совпадает с центром пикселя (оптимальная фаза);

2 - сдвиг объекта на половину размера пикселя по горизонтали (неоптимальная фаза);

3 - сдвиг объекта по вертикали. Результирующее распределение зарядов по пикселям второй сверху строки Z ( n ) для различных вариантов фазового сдвига:

1 - толстая линия, 2 - тонкая линия, 3 - штриховая линия

Математическое моделирование позволяет оценить визуально и количественно влияние фазы изображения на качество сигнала. Видно, что при малом размере изображения его сдвиги относительно структуры матрицы приводят к существенному изменению амплитуды сигнала. Двукратное расширение сигнала при неоптимальной фазе препятствует распознаванию близко расположенных объектов и ограничивает предельную разрешающую способность формирователей сигналов изображений на основе ПЗС и КМОП.

С ростом размеров минимальных деталей изображения по сравнению с размером пикселя Δ зависимость преобразованного сигнала Z ( n ) от фазы изображения существенно снижается, что видно на рис. 2 для квадратного изображения шириной в 2Δ.

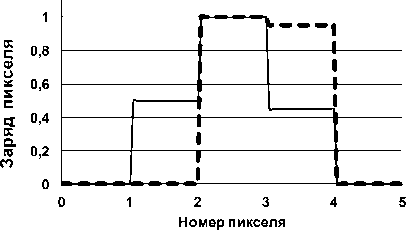
Рис. 2. Изменение распределения зарядов Z ( n ) по строке матрицы ПЗС при сдвиге изображения квадратного объекта шириной в 2Δ по горизонтали на Δ/2:

сплошная линия – центр изображения близок к центру пикселя, пунктир – центр изображения объекта находится рядом с границей между пикселями

Как видно, в этом случае амплитуда сигнала не зависит от фазового сдвига изображения объекта относительно структуры матрицы, а ширина сигнала при центре изображения на границе между пикселями совпадает с шириной объекта.

2.    Модель преобразователя периодических изображений

Существующие стандартизированные методы оценки разрешающей способности оптических и оптоэлектронных приборов [12; 13] основаны на использовании штриховых мир, позволяющих проектировать периодически меняющиеся изображения на поверхность фото-чувствительного устройства. Наиболее распространено использование так называемых прямоугольных мир с прямоугольной зависимостью пропускающей способности от координаты X в направлении, перпендикулярном штрихам миры (рис. 3).

Рис. 3. Прямоугольные штриховые миры с различной ориентацией штрихов

Такие миры можно изготовить с различной частотой штрихов. Пространственная частота штрихов миры ν определяется как число пар (белых и черных) штрихов на миллиметр.

Наряду с прямоугольными мирами используют и синусоидальные миры – с синусоидальной зависимостью пропускающей способности от координаты X , перпендикулярной направлению штрихов миры. Для моделирования преобразования в сигнал периодически меняющейся интенсивности излучения удобно использовать приведенную к дискретной структуре формирователя сигналов изображений пространственную частоту k = ν Δ, а размер пикселя приравнять к единице. Тогда приведенная частота Найквиста, при которой на размере пикселя укладывается одна полуволна, будет равна k_N = 0,5.

В нашей модели интенсивность излучения I ( x ), прошедшего сквозь синусоидальную миру, задается как:

I ( x ) = (1 + sin(2 πkx / Δ)) / 2. (1)

Модель прямоугольной миры описывается выражением:

I ( x ) = если(sin(2 πkx / Δ) > 10^–6; 1; 0). (2)

Слагаемое «1» введено в формулу (1), чтобы отразить тот факт, что интенсивность излучения I ( x ) имеет один знак, в отличие от знакопеременного сигнала в радиотехнике. Для бесструктурных преобразователей излучений, таких, как однородная мишень видикона, в диапазоне интенсивности излучения, обеспечивающем линейность преобразования, сигнал будет также синусоидальным. Это позволяет распространить методы анализа передаточных характеристик радиотехнических устройств на передаточные характеристики оптоэлектронных устройств. Но анализ передаточных характеристик ФСИ с дискретной структурой требует особого подхода ввиду алиасинга.

Условие sin(2 πkx / Δ) > 10^–6 введено в формулу (2), чтобы избежать неоднозначности знака синуса при его аргументе, кратном π. Согласно формулам (1; 2), максимальное значение облученности ПЗС в данной модели равно единице, а минимальное – нулю для обеих мир (рис. 4). Это облегчает вычисление характеристик передачи

ВЕСТНИК 2017

контраста ФСИ. В данной модели ФСИ коэффициент преобразования интенсивности излучения в выходной сигнал взят равным единице для равномерного облучения ПЗС.

X

Номер пикселя

Рис. 4. Облученность поверхности ПЗС через синусоидальную миру (толстая линия) и прямоугольную миру (тонкая линия) при пространственной частоте миры ν , равной частоте Найквиста, ν_N = 1/2Δ

ВЕСТНИК 2017

Величину сигнала в каждом пикселе мы определяем как интеграл от облученности в пределах площади данного пикселя. В этой модели мы рассматриваем идеальный одномерный преобразователь без учета эффектов расплывания заряда, чтобы в наиболее чистом виде изучить эффекты алиасинга.

Алиасинг при преобразовании периодически изменяющегося изображения проявляется в нарушении периодичности выходного сигнала (рис. 5). На рисунке показаны интенсивность изображения I ( x ) прямоугольной штриховой миры с пространственной частотой ν = 0,8 / (2Δ) и результирующий сигнал матрицы ПЗС.

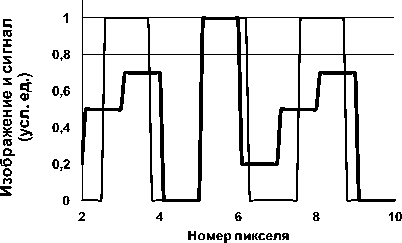
Рис. 5. Непериодичность сигнала Z ( n ) на выходе матрицы ПЗС (толстая линия) при преобразовании входного изображения I ( x ) штриховой миры (тонкая линия) с пространственной частотой на 20% ниже частоты Найквиста, ν_N = 1/(2Δ)

Как видно из рисунка, выходные сигналы от различных шпал миры различаются как по амплитуде, так и по ширине. Этот недостаток возрастает по мере приближения пространственной частоты ν миры к частоте Найквиста νN. Непе-риодичность выходного сигнала Z(n) при пре- образовании периодического изображения I(x) вносит в сигнал новый тип шумов – шумы алиасинга, зависящие от пространственной частоты изображения. В статье предложена методика оценки этих шумов.

С понижением пространственной частоты ν регулярность выходного сигнала ПЗС заметно возрастает (рис. 6). При ν < 0,6/(2Δ) алиасинг только несколько искажает форму сигнала, но не снижает заметно передачи контраста.

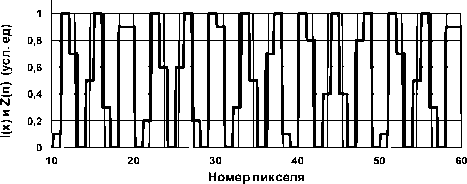
Рис. 6. Выходной сигнал матрицы ПЗС Z ( n ) (толстая линия) при пространственной частоте прямоугольной штриховой миры I ( x ) (тонкая линия), ν = 0,55 / (2Δ)

При частоте штриховой миры выше частоты Найквиста происходит пропадание сигнала от некоторых шпал миры. На рис. 7 показано, что заряд пикселя № 7 Z ₇ при неблагоприятной фазе совсем не отражает интенсивности излучения в соответствующей шпале: вместо четырех шпал в исходном изображении выходной сигнал показывает только три шпалы.

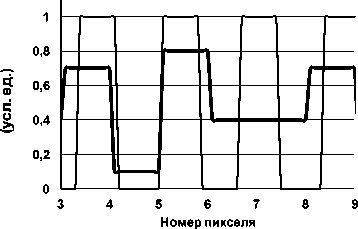
Рис. 7. Пропадание сигнала Z ₇ от одной из шпал при пространственной частоте штриховой миры ν = 1,2 / (2Δ): интенсивность изображения миры I ( x ) – тонкая линия; выходной сигнал матрицы ПЗС Z ( n ) – толстая линия

3.    Влияние алиасинга на функцию передачи контраста

Функция передачи контраста ФПК( ν ) определяется как:

ФПК( ν ) = ( Z max – Z min ) / ( Z max + Z min ),        (3)

где Z _max – максимальное значение выходного сигнала Z ( n ), а Z _min – минимальное.

При низкой пространственной частоте ν штриховой миры все максимальные значения и все минимальные значения выходного сигнала одинаковы. Поэтому нет проблемы определить значения Zmax и Zmin для формулы (3). Но при возрастании пространственной частоты ν выше 0,5 / (2Δ) алиасинг приводит к разбросу максимальных и минимальных значений Z(n), как это видно из рис. 8.

Для учета вклада алиасинга предлагается ввести три значения ФПК( ν ).

• •    Максимальное значение ФПК_max( ν ), определяемое через глобальный максимум и глобальный минимум Z ( n ) для всей миры.

• •    Минимальное значение ФПК_min( ν ), определяемое через глобальное минимальное значение среди всех максимумов Z ( n ) и через глобальное максимальное значение среди всех минимумов Z ( n ).

• •    Среднее значение ФПК_av( ν ), определяемое через средние от всех максимальных значений и от всех минимальных значений Z ( n ).

  

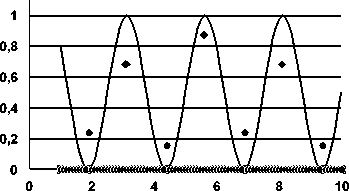
  Номер пикселя

  Рис. 8. Интенсивность облучения ПЗС через синусоидальную миру с пространственной частотой ν = 0,8 / (2Δ) (сплошная линия); максимальные значения сигнала (ромбы); минимальные значения сигнала (круглые маркеры)

  
  

Как видно, максимальные значения сигнала, как и минимальные значения сигнала, имеют разбросы своих значений. Поэтому значение ФПК_max( ν ), вычисленное через глобальный максимум и глобальный минимум Z ( n ), превышает значение ФПК_av( ν ), вычисленное через средние значения от максимумов и минимумов, а оба этих значения превышают значение ФПК_min( ν ), определяемое через глобальное минимальное значение среди всех максимумов Z ( n ) и через глобальное максимальное значение среди всех минимумов Z ( n ).

Стремление ФПКmin(ν) к нулю при приближении пространственной частоты синусоидальной миры к частоте Найквиста демонстрирует рис. 9, отражающий возросший разброс значений максимумов и минимумов сигнала при ν = 0,9 / (2Δ). Разница между максимальным значением пятого пикселя и минимальным значением шестого здесь стала существенно меньше разницы меж- ду глобальным максимумом десятого пикселя и глобальным минимумом второго.

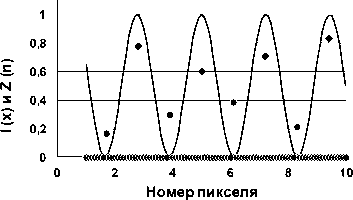
Рис. 9. Интенсивность облучения ПЗС через синусоидальную миру с пространственной частотой ν = 0,9 / (2Δ) (сплошная линия); максимальные значения сигнала (ромбы);

минимальные значения сигнала (круглые маркеры)

Найденные в результате компьютерного моделирования передаточных характеристик ФСИ на основе ПЗС функции передачи контраста изображены на рис. 10 в зависимости от отношения пространственной частоты миры к частоте Найквиста.

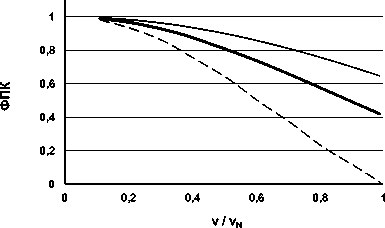
Рис. 10. Результат компьютерного моделирования – функции передачи контраста матриц ПЗС: максимальная (тонкая сплошная линия), средняя (толстая сплошная линия) и минимальная (штриховая линия), в зависимости от отношения пространственной частоты синусоидальной штриховой миры к частоте Найквиста

ВЕСТНИК 2017

Рис. 10 показывает, что найденная моделированием разрешающая способность, соответствующая минимальной функции передачи контраста, в два раза ниже, чем для максимальной функции. Это различие столь велико, что его невозможно игнорировать! Необходимо выяснить природу этого различия.

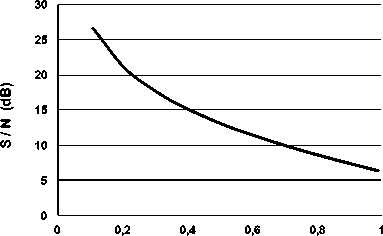
Найдя значения Z_{n max} и Z_{n min} при фиксированной пространственной частоте ν , находим среднеквадратичные отклонения Z_{n max} и Z_{n min} от своих средних значений: Δ Z_{n max} и Δ Z_{n min}. Среднеквадратичное значение от этих величин дает оценку шума алиасинга, N (рис. 11). Выражение для отношения сигнала к шуму в децибелах имеет вид:

S / N = 10 log (ФПК _av ( ν ) / N ).              (4)

ν / ν N

Рис. 11. Вклад алиасинга в отношение S / N в зависимости от отношения пространственной частоты к частоте Найквиста

ВЕСТНИК 2017

4.    Теоретические значения ФПК(v) для синусоидальной миры

Интегрирование распределения интенсивности облучения по площади пикселя при оптимальных фазах светлого и темного штрихов дает:

ФПК_max( ν ) = sin( πν Δ) / ( πν Δ). (5)

Для неоптимальных фаз светлого и темного штрихов относительно дискретной структуры матрицы получаем:

ФПК_min( ν ) = sin(2 πν Δ) / (2 πν Δ). (6)

Усреднение по фазам светлого и темного штрихов относительно дискретной структуры матрицы требует повторного интегрирования, аналогичного используемому при выводе формулы (5), поэтому приходим к:

ФПК_av( ν ) = (sin( πν Δ) / ( πν Δ))². (7)

Теоретические значения ФПК (5)–(7) прекрасно соответствуют значениям, найденным в процессе компьютерного моделирования и изображенным на рис. 10.

Максимальное значение ФПК_max( ν ) совпадает с теоретической оценкой функции передачи модуляции дискретного ФСИ, часто встречающейся в литературе, которое дает завышенную оценку разрешающей способности ФСИ. Компьютерное моделирование ФСИ позволяет понять причину широко распространенной излишне оптимистической оценки разрешающей способности ФСИ с дискретной структурой. Выбор среди максимальных значений Z_{n max} глобального максимума и далеко отстоящего от него глобального минимума Z_{n min} совсем не отражает передачи контраста соседних светлого и темного штрихов миры. Поэтому применение формулы (5) для оценки разрешающей способности дискретного ФСИ некорректно!

Минимальное значение ФПКmin(ν) по формуле (6) правильно оценивает предельную разрешающую способность ФСИ, если требуется передать мельчайшие детали изображения. Это бывает важно при использовании ПЗС в научных приборах и в аппаратуре космического наблюдения и астрофизических исследований.

Среднее значение ФПК _av ( ν ) по формуле (7) дает реалистическую оценку разрешающей способности ФСИ, особенно при наложении повторяющихся кадров в цифровом телевидении, где наложение кадров может обеспечить усреднение фаз изображений по отношению к дискретной структуре преобразователя.

Идея наложения кадров со сдвигом изображения на долю пикселя может быть положена в основу построения ФСИ дискретного типа со сверхразрешением.

Заключение

• 1.    Компьютерное моделирование матричного формирователя сигналов изображений (ФСИ) на базе ПЗС позволило выяснить характер влияния алиасинга на передаточные характеристики ФСИ.

• 2.    Предложена система из трех функций передачи контраста ФСИ, по-разному учитывающих фазовые соотношения между изображением штриховой миры и дискретной структурой матрицы ПЗС:

• 1)    максимальная ФПК для оптимальных фаз;

• 2)    минимальная ФПК для неоптимальных фаз;

• 3)    средняя ФПК, дающая оценку разрешающей способности ФСИ по всей площади миры.

• 3.    Максимальная ФПК для синусоидальной миры совпадает с известной в литературе оценкой функции передачи модуляции дискретного фотоприемника, которая дает слишком оптимистическую оценку значений ФПК.

• 4.    Минимальная ФПК дает оценку предельных возможностей ФСИ и может быть рекомендована в качестве критерия оценки качества ФСИ.

• 5.    Средняя ФПК дает реалистичную оценку средних возможностей ФСИ и точку отсчета для оценки шумов алиасинга, зависящих от пространственной частоты миры.

• 6.    Предложен метод оценки шумов алиасинга, возрастающих по мере приближения к пространственной частоте Найквиста.

• 7.    Разработанная модель ФСИ может быть использована при разработке методик оценки качества ФСИ и в процессе проектирования ФСИ со сверхразрешением.

Все три ФПК найдены в результате компьютерного моделирования и прекрасно соответствуют полученным в этой работе теоретическим зависимостям.