Моделирование аналоговой синхронизации апериодических псевдослучайных последовательностей на каналах низкого качества

В системах защиты информации широкое применение находят АПСП, которые синхронно и синфазно вырабатываются на передающей и приемной сторонах связи. На каналах низкого качества, когда модем не в состоянии выделять дискретные посылки сигнала, возникает потребность в аналоговой синхронизации АПСП. Рассмотрим аналоговую синхронизацию датчиков АПСП. Пусть реализация пускового ПС-ФМ-сигнала имеет вид:

сигнала; Т - длительность элемента сообщения; y_k = (0,1) – псевдослучайная последовательность, не известная противнику (гамма).

В канале присутствует аддитивная помеха ε(t) с произвольным законом распределения, нулевым средним и дисперсией σ² . Тогда на интервале анализа аналоговые отчеты сигнала будут иметь вид:

^ i =

a (-1) Yi + Ei

I ^£ i ,

, если i принадлежит ПC;

если i не принадлежит ПC,

a = 0 , mo S 1 ( t ) = П ( t ) U c = cos ( o, t + ^ ) ,

где а - амплитуда сигнала; γ_i = (0, 1) - равновероятные и взаимно независимые случайные величины;

a = 1, mo S 2 ( t ) = - S 1 ( t ) ,       0 <  t <  T ;

γ _k

, (1)

k

n( t ) = ](—1) ,

( k - 1 ) T₀ <  t <  kT₀ , k = 1,2,3 ... B при других t

iT 0

Ej = J E (t )• cos (0c tdt

( i - ¹ ) T o

–

где: U_c - амплитуда сигнала; Т_с - длительность субэлемента

произвольно распределенная случайная величина с нулевым средним и дисперсией σ² .

Предположим, что пусковая комбинация (ПК) известна на приеме и состоит из N символов: S₁ , S₂ ,..., S_N . На приеме осу-

ществляется автокорреляционный прием пускового сигнала по правилу:

получим границу для вероятности неприема СП в виде:

N

^X U + j ■ 5 , ><  U 0 .

i = 1

P_h <  min g ( t ) , npu t <  0 ,

Здесь U₁ , U₂ ,…, U_L , принятые из канала, L двоичных символов, а S₁ , S₂ ,…, S_N - известная пусковая комбинация, состоящая из N двоичных символов.

Требуется определить вероятность неприема синхропосылки (СП), если известно, что вся пусковая комбинация вхо-

t где g (t) = M t e

Nγ a (N-R(T))+X(-1) '• П i=1

,

дит в интервал анализа.

математическое ожидание g(t) вычисляется относительно γ_i и η_i , i = 1, 2, 3,…,N .

Найдем математическое ожидание относительно γ_i :

Рассмотрим случай, когда пусковой и опорный сигналы пересекаются. Тогда можем составить две суммы:

N           γ N           γγ

• 1)    X U-1 )' = E ( a ( - 1 )' + 4( - ¹ ) =

i=1                      ,=1 V.

N γ

= aN + X 8i (—1) ;

i=1

N               N - T r-.

• ²⁾    X ^ ⁽ - ¹ ) ^Y = X a ^{( - 1} ) ^{Y + T +} 8 + T *^{( - 1} ) ^{Y i +}

• i=1                    ,=1 LJ

T

+ X 8'+T •(-1)Y = i = N - T+1

N - TT

= aR (T)+ X (-1 г •8t+T + X (-1 Г ■8t+T)(5)

i = 1                        , = N - T + 1

M ^

t •

e

a ( ^N - ^R ( ^T ) ) +₍ ^N ( " I ) ^Y Pi

t • a [ N - R ( t ) ] n

= e • П ch ( ^t • n i )

= 1

t • ^a [ N - ^R ( t ) ] n

I = e         •П

= 1

t • a [ N - R ( t ) ]+ у N n , <  e                ¹= ¹

Неравенство (10) получено из условия

2 x ch(x)< e2 .

tη e , + e

- n

.

Учитывая, что η_i центрированная, выражение (10) можем переписать как:

g ( t ) <  e ' a t n - R ( t ^{) ]}+ t 2 ^- №2

где R(T) - автокорреляционная функция ПСП при сдвиге, равном Т .

Очевидно, неприем может произойти только тогда, когда первая сумма (4) будет меньше второй суммы (5):

N          Y.               N - ^T        Y-             T          Y-

P = P aN + X 8 ( - 1 ) ' < ^a • R ( T ) +X ( - 1 ) 8 _r+ X ( - 1 ) • 8 Lt н                  =1                            =1                ¹ , = N - T + 1                T

= P

( n - t       y-                    t Y-

^{N - R} ( ^T ) ) ^{+ X ( - 1} ) • ^{( 8} , ^{- 8} , + T ^{) + X ( - 1} ) ' ( ⁸ i ^-8 i ' + T ) = I                            = = N - T + 1

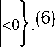
Учитывая, что под обоими знаками суммы в правой части неравенства (6) стоят случайные величины с нулевыми средними и одинаковыми дисперсиями, равными 2σ2, фор- мулу (6) можем переписать как:

N

P h = P h( N - R(T )) + X ( - 1) ^Y - • n <  0 I- ,

, = 1

где:

(8 , - 8 , _{+ T}) npu , = 1,2,3 ,..., N - T ;

( 8 , - 8 , _{+ T} ) npu i = 1,2,3,..., N .

Учитывая слабую коррелированность помехи на интервале субэлемента сигнала, предполагается взаимная независимость отсчетов η_i и поэтому для оценки (7) используем границу Чернова в виде:

P { x <  b } <  g ( t ) • e ^Bt , t <  0 , где g ( t ) = M { e^tx } .

Полагая в (8)

N x = a •[N - R(T')]+X (-1)Yi • П- M B = 0, i=1                 1

Легко показать, что показатель степени в (11) минимизиру- ется при:

- a •[ N - R ( T ) ] ^{t onm} =      2N • ^ ²

тогда окончательно имеем:

- a² [ N-R(T) ] ² + a [ N-R(T) ] ²         H² [ N-R(T) ] ²

P <  min g ( t ) = e" ^{8 2} • ^{2N     5 2} • ^4N = e 4N , ⁽¹2)

н      t <  0

где H² = a²/ σ ² - отношение средней энергии элемента сигнала на входе приемника к спектральной плотности помехи. Для оценки вероятности неприема ПК на всем интервале анализа L используем аддитивную границу Буля [1], тогда окончательно получим:

HN N-L H² [ N-R(T) ] ²

P _H <  ( L - 2N ) • e ⁴ + X e ^4N .               (13)

=1

Неравенство (13) дает строгую верхнюю границу для вероятности неприема ПС при произвольных помехах в канале. Представляет интерес рассмотрение некоторых частных-случаев, например, когда помеха в канале типа белого гауссовского шума (БГШ).

Вывод точной формулы для вероятности неприема ПК в условиях гауссовских помех

В частном случае, когда помеха гауссовская с нулевым средним и с дисперсией δ² легко получить точную формулу. Для этого (7) представим как:

МЕТОДЫ

р„-рЩ-^ -П^^-Р^^

-p^>aVN-R(T)Y

где

Л=^~^ ^pi -

гауссовская величина с нулевым средним и дисперсией равной 2Nσ² .

Тогда для (14) можем получить точную формулу в виде [2]:

PH=P{ri>a[N-R(T)]}= J --^=.e^dx =

a[N-R(T)] 26 kN              (15)

1-F

"aVN-RW /SjlN

= 1-F

H[N-R(T)]

где

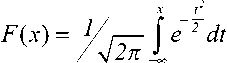
- интеграл вероятности.

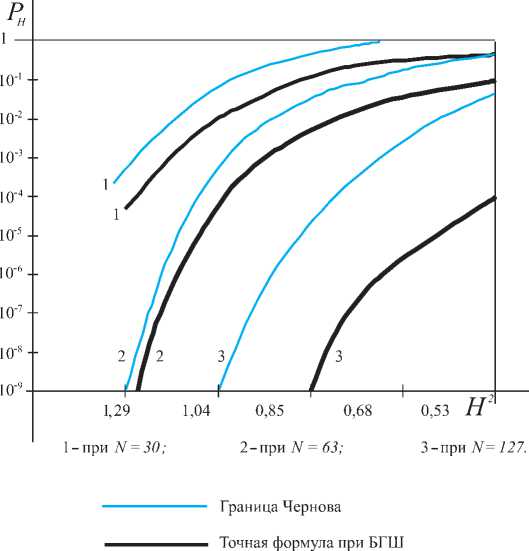
Рис. 1. Границы вероятности неприема ПК

Для определения вероятности неприема пускового сигнала на интервале анализа, опять воспользуемся аддитивной границей и получим окончательное выражение в виде:

<(L-2NV

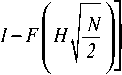
+ Z

' H\.N-R(nA 42N

Известно, что в классе помех с произвольным законом распределения, гауссовская помеха всегда дает нижнюю границу для вероятности ошибки [1].

Поэтому выражение (16) можно рассматривать как нижнюю границу вероятности неприема ПК в случае произ-вольныхпомехвканале.На рис. 1 приведенынижняяиверх-

няя грaницы вероятности неприема ПК К-Ф²) для различных N при аналоговом запуске и произвольных помехах в канале, рассчитанные по (13) и (16) соответственно. Из анализа кривых, приведенных на графике, видно, что верхняя граница (13), полученная с использованием неравенства Чернова, дает достаточно плотные результаты ( к ривые 1 и 2) и, следовательно, будет хорошей оценкой p при произвольных слабо коррелированных помехах в канале ■