Моделирование асинхронных бизнес-циклов, основанное на метаморфозной модели Г. Менша

⟡ ⟡ ⟡

С развитием и усложнением экономик государств все чаще возникает проблема асинхронности циклических процессов. Система макроэкономических показателей не является идеальной, в связи с чем отклонения от тренда в ней лишь условно описываются гармоническими колебаниями. Таким образом, предложенная в первой половине XX века теория длинных волн Н.Д. Кондратьева, а также основанная на ней теория инновационного развития Й. Шумпетера [7] требуют новых подходов для описания циклической компоненты. Целью данной работы является разработка математической модели, описывающей влияние инновационных процессов на цикличность экономического развития.

Теоретическое решение рассматриваемой проблемы было найдено Г. Меншем в 1970-х годах. Предложенная им метаморфозная модель циклов изменения структуры связывает динамику технологических и экономических процессов. Г. Менш предложил модель [4], которая отражает идею, что экономика развивается через серию прерывистых инновационных импульсов, принимающих форму последовательных S-образных циклов. Метаморфозная модель Г. Менша соединяет в себе кумулятивные и потоковые процессы экономической динамики. На рисунке 1 видно, что экономическому и технологическому развитию соответствуют разные тренды, взаимодействующие между собой. Начало фазы спада в экономике подавляет жизненный цикл соответствующего технологического поколения, и, наоборот, насыщение существующего технического уклада негативно сказывается на экономических трендах. Аналогичная связь наблюдается в фазе роста, но в обратную сторону.

ГРНТИ 06.35.51

Александр Александрович Петряков – аспирант Санкт-Петербургского государственного экономического университета.

Согла с но Меншу, базисные инновации приводят к появлени ю новых с т руктурооб р азующих отраслей, развитие которых дает с игнал к о ж ивлению и росту эко н омики. Та к им образо м , прорывные нововвед е ния способствуют вы х оду из деп р ессии, и, как следств и е, увеличе н ию уровня потребления. Новый к р изис нарушает проце с с расшире н ия национ а льного хозяйства, об ъ емы инвес т иций снижаются, а с б ережения наоборот р а стут. На о с нове теории Менша м о жно сдела т ь вывод о том, что экономика подвержена влиянию 2 взаимоза в исимых процессов - и нвестиров а ния и сбе р ежения, что необходи м о учесть при построе н ии матема т ической модели.

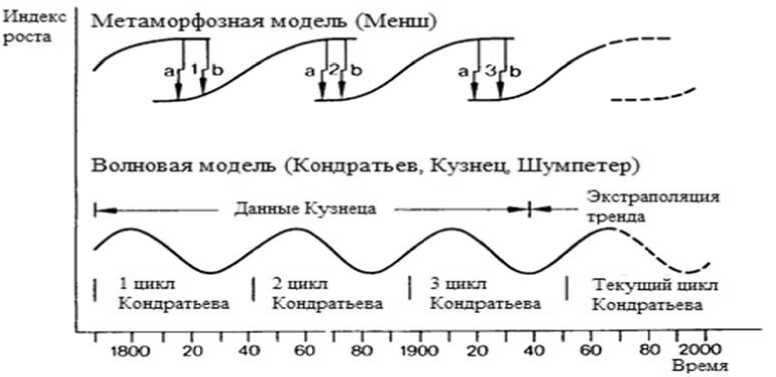
Рис. 1. Мета м орфозная м о дель промышленной эво л юции Мен ш а [4]

В статье [8] для бизнес-цикл о в рассмот р ена двумер н ая модель Кальдора - Калецкого:

Г dY

J dt | dK V Hi

= a[l( Y (t),K(t)^ - S(Y(t),K ( t)^A

= l{Y( t -T),K(t))-6K(t)

Здесь Y - валовый продукт, I - инвест и ции, S - сбережения, K - основн о й капитал, T - интервал задержки, а- коэффициент пропорциональ н ости, 8- степень обесценивания к а питала. В р аботе [2] для исследования циклических тенд е нций на о б лигационн о м рынке рассмотрена м одель:

f ^ = fc(t)[B(t)-4(t)]

dt

« ^t = m(t)[P ‘ (t) + l(t,P(t)^ A (t)

^_t = - n (t)[P ‘ (t) + l(t,P(t)) B (t)

Здесь P - уровень цен обли г аций; B - с ила спроса, характери з ующаяся с коростью и зменения количества облигаций, заявленны х на покуп к у; A - сила предложе н ия, харак т еризующаяся скоростью изменени я объема облигаций, з а явленных н а продажу; k, m, n - коэффициен т ы пропор ц иональности, l - параметр опережения/запазд ы вания. Дл я моделиро в ания дина м ики валов о го продукта рассмотрим систему д ифференциальных ура в нений:

Tt = ^{a(y- V ) +} ^

аи_ =„ {№_ at " \dt ^ = -у^

-

-

^

■ ^2)^

Здесь Y(t) - объем выпуска п р одукции ( у ровень ВВ П ), U(t) - т е мпы роста и нвестиций, V(t) - темпы роста сбе р ежений (свободных д енежных с р едств), ц, Хь Х 2 - пар а метры реа к ции запаздывания инвестиций и сбережений на измен е ния в экон о мике, а, в, Y - коэфф и циенты пр о порциона л ьности. Компактная м атематическая запись в виде сист е мы (1) имеет следую щ ую эконом и ческую ин т ерпретацию: динамика валового продукта за в исит от ди с баланса ин в естиций и сбережени й . Наращив а ние инвести-

ций обеспечивает рост экономики. Увеличение объема сбережений ведет к сворачиванию экономики. Совпадение темпов инвестиций и сбережений обуславливает равновесное состояние.

Динамика инвестиций и сбережений пропорциональна скорости изменения валового продукта, но с некоторым сдвигом, который возникает в силу инерции и запоздалой реакции на макроэкономические перемены. Решение системы (1) для Y(t) является суммой линейной функции и композиции функций тангенса и арктангенса и имеет следующий вид:

F⁽0 = Xt + C + ^=arctg^ ,

y(_t) = ^arc^ V^i!!^    • ^t ₃ ( _A +.^⁽ ₃ - _Х ) г ^ _у _ _аг_в г ⁽ _{р + У} )- (S^[E^^

Эта композиция циклична и скачкообразна в силу периодичности и разрывности тангенса. Кроме того, график этой композиции имеет S-образный вид как у арктангенса. Следовательно, графическое изображение функции y(t) можно интерпретировать как волны Менша. Отсюда заключаем, что система (1) позволяет моделировать влияние инновационных волн на траекторию экономического роста.

Значения коэффициентов α, β, γ, μ, λ подбираются на основе статистических данных по ВВП, инвестициям и сбережениям за длительный период времени. В формуле для Y(t) содержатся произвольные числа A, B, C, которые являются элементами настройки модели. С помощью A модель приводится к нужной начальной дате. С помощью B подбирается нужный размер цикла. С помощью C выбирается начальное значение ВВП.

Верификация модели производилась на основе статистических данных США, предоставленных Бюро экономического анализа (Bureau of Economic Analysis). Для проверки используется статистика по ВВП, валовым инвестициям, а также личным сбережениям, рассчитанным по методике NIPA. Все значения взяты в сравнимых ценах с целью нивелировать влияние инфляции. Результаты моделирования отображены на рисунках 2 и 3.

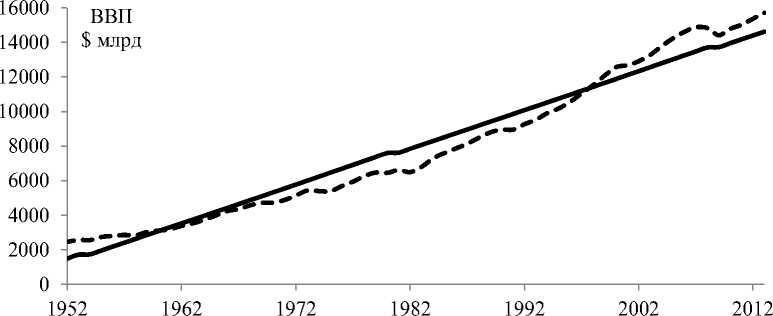
Рис. 2. Динамика ВВП США

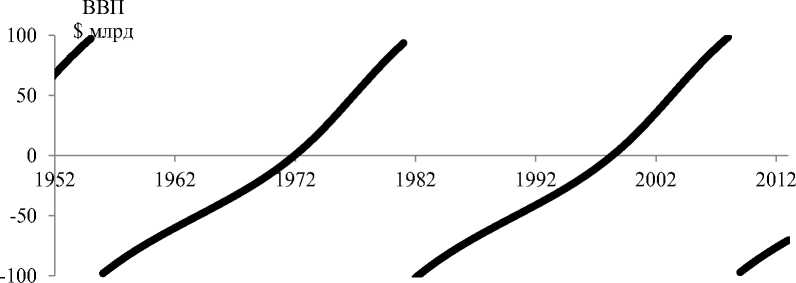
Рис. 3. Смоделированные волны Менша

Сравнение рисунков 1 и 3 демонстрирует качественную идентичность поведения теоретической и практической волн Менша. Сравним построенный с помощью модели график ВВП с реальным изменением ВВП. Как видно из таблицы, модель имеет достаточно серьезную для ВВП ошибку прогноза, ее среднее значение за последние годы 7,54%. Таким образом, предложенная модель строит волны Менша, которые качественно адекватны реальности. Но существенное различие в масштабе требует дальнейшей доработки модели.

Таблица

Ошибка прогнозирования ВВП

Год	2006	2007	2008	2009	2010	2011	2012	2013
ВВП США	14 613,8	14 873,7	14 830,4	14 418,7	14 783,8	15 020,6	15 369,2	15 710,3
Модель ВВП	13 244,48	13 472,27	13 699,25	13 721,56	13 947	14 171,83	14 396,13	14 620,03
Ошибка прогноза	10,34%	10,40%	8,26%	5,08%	6,00%	5,99%	6,76%	7,46%

Подводя итог, укажем, что результатом работы является математическая модель, включающая в себя инновационные волны Г. Менша и качественно отражающая динамику бизнес-циклов Соединенных Штатов. Модель подтверждает основные идеи, изложенные Г. Меншем в своей теории, хорошо согласуется с наработками других исследователей [1; 3; 5; 6; 7]. Таким образом, полученную модель можно считать в целом достоверной, т.к. она отражает основные тезисы теории инновационного развития. С другой стороны, модель не лишена недостатков. К ним можно отнести: существенное различие в масштабе между теоретическими и реальными значениями; необходимость верификации полученной модели на экономике других стран; сложность расчетов параметров модели.

Помимо возможности моделирования инновационных волн, по результатам исследования получен вывод о том, что новая инновационная волна в экономике США возникает примерно каждые 30 лет. Таким образом, обладая ретроспективной информацией, с помощью модели можно математически спрогнозировать состояние экономики в ближайшем будущем.