Моделирование атмосферных течений над горным рельефом

Незнание состояния и поведения атмосферы над горным рельефом, неготовность пилотов к полётам в условиях орографической турбулентности приводят к лётным происшествиям и катастрофам [1–3].

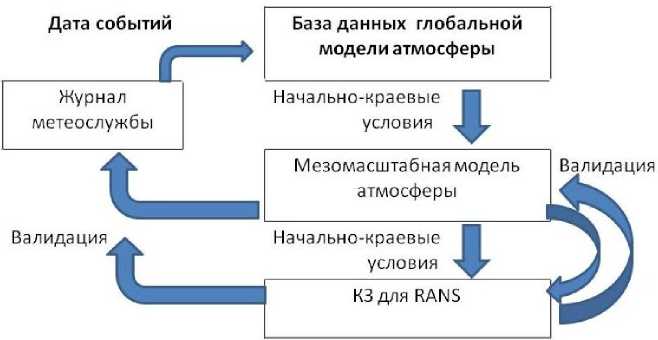
Рис. 1. Технология моделирования

Для подготовки пилотов к полётам в условиях орографической турбулентности необходимы авиатренажеры и пилотажные стенды, моделирующие воздействие на самолёт турбулентных порывов. Для этого нужны надежные математические модели, адекватно воспроизводящие атмосферные течения в рамках краевых задач для соответствующих уравнений, причём сложность постановки задач должна соответствовать уровню точности и подробности имеющихся граничных условий. Таким образом, моделирование атмосферных течений над горным рельефом и учёт атмосферного фактора в моделях динамики авиационных тренажёров является актуальной задачей.

В предлагаемой технологии моделирования атмосферных течений в качестве начальнокраевых условий используются данные о состоянии атмосферы, полученные из мезомас-штабной модели атмосферы, для запуска которой используется база данных глобальной модели атмосферы. Выбор характерных сценариев и даты моделирования производится на основании анализа журнала метеослужбы аэродрома (рис. 1). Результаты моделирования в мезомасштабной модели и в рамках краевой задачи в зоне аэропорта сравниваются между собой и с записями журнала метеослужбы аэропорта.

2.    Постановка задачи

Решается краевая задача для осредненных по Рейнольдсу уравнений Навье–Стокса (RANS) с моделью турбулентности SST. Полная система уравнений приведена в работе [4]. Для постановки граничных условий необходимо задать профили скорости ветра, температуры, энергии турбулентности и скорости её диссипации в зависимости от высоты над землей г.

При этом следует помнить, что турбулентные течения являются неньютоновой жидкостью. Вопрос справедливости уравнений Навье–Стокса (линейная связь между тензорами скоростей деформаций и напряжений) при возникновении турбулентности остаётся открытым.

Осреднение по Рейнольдсу опирается на гипотезу эргодичности: вместо интегрирования по пространству (спектров по пространству) выполняется интегрирование по времени (спектры по времени). В соответствии с гипотезой эргодичности осреднение по ансамблю из N реализаций заменяется осреднением по времени, где интервал осреднения существенно превышает характерное время энергосодержащих турбулентных пульсаций и много меньше характерного времени осредненного течения. Гипотеза эргодичности нарушается, по крайней мере, в ходе обратного каскадного процесса формирования крупных атмосферных вихрей. Таким образом, решается краевая задача, не имеющая доказательства корректности, и валидация численного метода строго обязательна.

Вопрос корректности разностной задачи для уравнений Навье–Стокса остается открытым из-за неясности граничных условий. Известны примеры неединственности численных решений из-за численной постановки граничных условий. Физически необоснованные и математически необоснованные граничные условия могут приводить к неустойчивости численного решения (например, на выходной границе). Всё это обуславливает необходимость верификации численной схемы.

В тех случаях, когда мезомасштабная модель атмосферы для данного участка земной поверхности не может быть запущена, а также для верификации численной схемы, могут понадобиться профили атмосферных параметров, заданные аналитически.

По результатам проведенного обзора литературы [5–9 и др.] и численных исследований получено, что наиболее подходящий профиль скорости ветра выражается системой (1):

и = ^ ln (^) cos(a), Х2 к го /

^ 1       ⁺

v = ln ------ sin(a),

Х 2

^и = ^v - ? ^P lr e ^exp (- V iS^{( г} - ^{h )}^^cos [V iS^{( г} - ^{h ) +} 5

^{( г}< ^{h )} ,

-

,

^v=I VhE^exp ( ^- V ih ^{( г - h )} ) ^sin [Vs ^{( г - h )+ 5 - q} ] ,

^{( г} > ^{h )} ,

где и и v — продольная и поперечная составляющие скорости, ki = xv* — значение коэф-ди _               _ _ фициента турбулентности на единичной высоте, v* = хг^--динамическая составляющая дг

скорости, х — универсальная безразмерная постоянная, г о — шероховатость подстилающей

поверхности, численные значения которой приведены в [10], V_g =

1 др ш _г рду

— геострофи-

ческий ветер, а — угол между направлением геострофического ветра и ветра в приземном

подслое, Һ — высота приземного подслоя, ш _г — угловая скорость вращения Земли. Профили скорости (1) имеют два участка: приземный подслой (до 100 м) и пограничный слой (1–1,5 км) с различными коэффициентами турбулентности:

{ к 1 г, г <  Һ ;

kih, г > Һ.

Приведенная зависимость для коэффициента турбулентности была предложена М.И. Юдиным и М.Е. Швецом в [11]. Выбор профиля скорости опирается на материалы работы [12]. Выбор профиля температуры основан на теории Монина–Обухова (см. [1]).

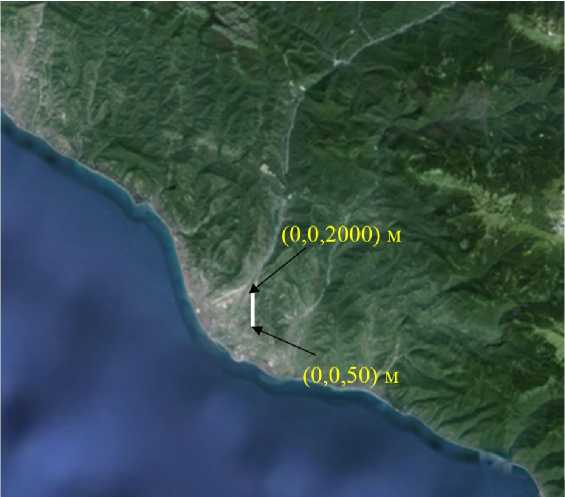
Рис. 2. Линия, ортогональная ВПП, вдоль которой сравниваются результаты

Для расчета параметров атмосферы при обтекании рельефа в работе [13] граничные условия задаются вдалеке от интересующей области, а рельеф специально сглаживается при приближении к границам. В этом случае на границах можно задавать условия как над ровной поверхностью, не учитывая особенности рельефа местности. Влияние рельефа проявляется уже непосредственно при моделировании течения в расчётной области.

При использовании данных, получаемых с помощью мезомасштабной модели атмосферы COSMO-RU07 [14], на первом шаге проводится расчет области, характерный размер которой порядка десяти тысяч километров, на расчетной сетке с шагом 20 км. Граничные условия выбираются с помощью глобальной квазистатической модели атмосферы GME (разработка Метеослужбы Германии) [15] или с помощью глобальной модели IFS Европейского центра среднесрочных прогнозов. На следующем шаге проводится расчет меньшей области величиной порядка тысячи километров на сетке с шагом 7 км. Затем расчеты производятся на еще более мелкой сетке с ячейкой 1 км и на области размерами порядка сотни километров.

Данный подход позволяет использовать граничные условия, специфичные именно для данного региона. Таким образом, удается избежать искусственного сглаживания рельефа.

Постепенное уменьшение размеров ячеек способствует увеличению точности и экономии вычислительных ресурсов.

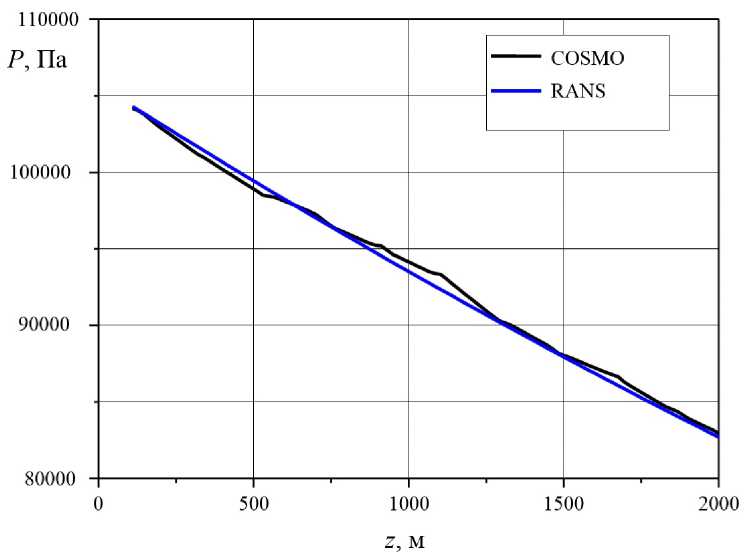
Рис. 3. Профили давления (модель COSMO и RANS-моделирование)

В модели COSMO учитываются такие факторы, влияющие на течение, как солнечное излучение, парообразование, образование капель, дождь, облака, силы тяжести, силы Архимеда и Кориолиса и т.д. Учет данных эффектов является критическим в ряде случаев. Так, в работе [12] показано, что в условиях близости горного аэродрома к морю является необходимым учет конденсации капель.

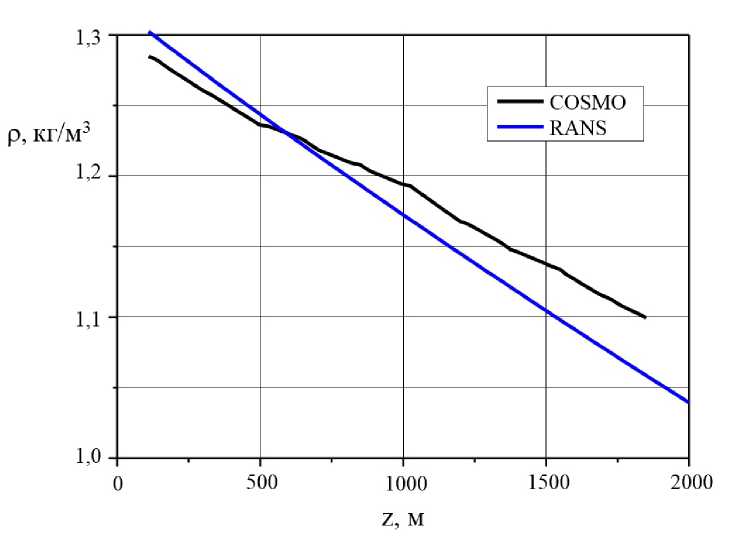
Рис. 4. Профили плотности (модель COSMO и RANS-моделирование)

В предлагаемой методике параметры течения, рассчитанные с помощью модели COSMO-RU07 в большой области, используются в качестве граничных и начальных условий для расчета воздушного течения в подобласти горного аэродрома. Это позволяет получить течение, согласованное с глобальным течением атмосферы.

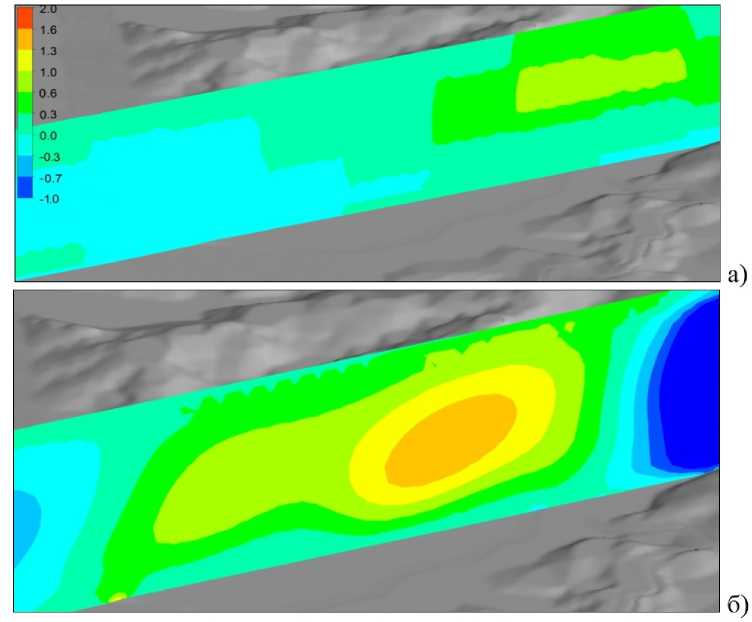
Рис. 5. Поля вертикальной компоненты скорости (м/с) в плоскости симметрии ВПП: а) данные COSMO; б) результаты RANS-моделирования

Для валидации результатов расчёта можно использовать данные о течениях над горным рельефом, полученные с помощью летающей лаборатории, которая представляет собой самолет с необходимыми приборами для измерения параметров атмосферы. Самолет подобного типа может измерить поля скоростей, температуры, влажности, давления, распределение капель по размерам и прочее в большой области за время, за которое параметры атмосферы не успевают существенно измениться. В этом случае собранные данные могут служить для верификации решения начально-краевой задачи для системы уравнений Рейнольдса и валидации предлагаемой технологии. Летающая лаборатория имеет преимущество перед традиционными и широко распространёнными шарами-зондами, позволяющими измерять параметры атмосферы только в районе привязки зондов.

3.    Результаты расчета

В качестве примера приведен результат численного моделирования в рамках краевой задачи для уравнений Рейнольдса течения сжимаемого (совершенного) газа над горным ландшафтом в районе аэропорта Адлер. Пограничный слой считался полностью турбулентным. Для замыкания системы уравнений использована двухпараметрическая SST-модель турбулентности. Набегающий поток был задан граничным условием типа Inlet [16]. Профили скорости (три компоненты) и статической температуры, а также распределение температуры на подстилающей поверхности заданы по данным Росгидромета. На подстилающей поверхности выполняется условие прилипания.

Проведенные расчеты позволили произвести сравнение ряда моделируемых параметров с исходными (начальными) данными, предоставленными Росгидрометом и полученными с помощью COSMO. Результаты численного моделирования приведены на рис. 2–5. Они хорошо передают ветровую обстановку в окрестности взлетно-посадочной полосы (ВПП). Расхождения можно объяснить различиями решаемых уравнений, численных схем и расчётных сеток.

4.    Выводы

Разработана технология моделирования атмосферных течений над горным ландшафтом в районе выполнения полётов. Приведены результаты расчета в районе аэропорта Адлер. Полученные результаты нашли применение в пилотажных стендах и авиационных тренажёрах при модификации моделей динамики с учётом атмосферного фактора.

Данная работа выполнена в рамках Проекта «Разработка программно-аппаратного комплекса реалистичного восприятия летчиком сложных режимов полета и оценки его психофизиологического состояния» (Договор № 02.С25.31.0017 между ОАО РСК «МиГ» и Министерством образования и науки РФ об условиях предоставления и использования субсидии на реализацию комплексного проекта по созданию высокотехнологичного производства, выполняемого с участием ФГАОУ ВПО МФТИ (ГУ)).