Моделирование автоматизированных информационных систем на основе вероятностных автоматов с блокировкой обслуживания

В.Е. Белоусов, , Д.В. Дорофеев, А. Можарова,

V.E. Belousov, , Dorofeev, Mozharova,

Информационные системы, подлежащие исследованию, весьма разнообразны по своей структуре, сложности, конкретному назначению и обладают большим разнообразием. Однако если отвлечься от конкретного производственного смысла процессов, протекающих в системах и их отдельных узлах, то логические и вычислительные правила функционирования элементов систем будут не столь разнообразны. Во многих случаях, казалось бы, совсем разные «по конкретному смыслу» элементы функционируют на основании одних и тех же законов. Это дает возможность при построении автоматных моделей сложных систем выделить определенное, сравнительно небольшое количество стандартизированных автоматов (вероятностных и детер- минированных), так что построение моделей довольно широкого класса систем оказывается возможным лишь с помощью определенного набора автоматов этих типов [1].

Постановка задачи автоматной интерпретации

Разберем различные способы автоматной интерпретации моделей различных узлов информационных систем. При этом некоторые узлы будут имитироваться в виде отдельных автоматов, другие – с помощью небольших вероятностно-автоматных систем. Предварительное изучение отдельных свойств типовых узлов информационных систем дает возможность перейти в дальнейшем к описанию построения моделей довольно сложных систем. Одним из наиболее характерных свойств информационных систем является поступление на вход системы некоторых транзакций, которые в каждом отдельном случае могут иметь различный конкретный смысл. Как известно, правила формирования входящих потоков могут быть довольно разнообразными [2].

На практике активные и пассивные задержки транзакций внутри информационных систем в процессе их функционирования, как правило, сопровождаются влиянием различных специфических особенностей: блокировки, резервирования и др. Рассмотрим описание моделей ряда систем, обладающих такими особенностями. Попутно коснемся построения индикаторов, служащих для определения различных неслучайных характеристик моделей. Постараемся отразить две сходные особенности системы: блокировку на обслуживающий механизм и на поступление тран-зактов. Разберем случай, когда транзакты, поступившие в систему и заставшие обслуживающий механизм занятым, не покидают ее, а задерживаются, образуя очередь. Пусть промежутки времени между моментами поступления последовательных транзактов – взаимно независимые одинаково распределенные случайные величины, реализации которых можно рассматривать как реализации некоторой случайной величины ^. Сделаем такое же предположение и относительно длительностей обслуживания, считая их реализациями случайной величины п. Очередь предполагается неограниченной [3].

Для того чтобы полностью охарактеризовать систему в каждый момент времени, необходимо задание трех ее временных характеристик. Они могут быть выбраны, например, следующим образом: 1) промежуток времени от момента t до момента поступления очередного тран-закта; 2) промежуток времени от момента t до момента окончания обслуживания того транзак-та, который обслуживается в момент t; 3) количество транзактов, ожидающих в очереди, в момент времени t.

Эти три характеристики, очевидно, образуют Марковский вектор системы [4], следовательно, автоматную модель системы можно построить из трех автоматов Л_ъ Л₂ и Л₃, состояния которых отождествим соответственно с тремя этими временными характеристиками. Будем считать, что при значении выходного сигнала %_l(t) автомата A_l, равном 1, через одну единицу времени (в момент t + 1) поступит очередной транзакт. Далее, х₂ (t) = 1 лишь в том случае, если обслуживающий механизм свободен в момент t или освободится к моменту времени t + 1. Выходной сигнал х₃ (t) равен 1, если в момент t в очереди имеются транзакты.

На основании такого выбора состояния автоматов и значений выходных сигналов систему функций выходов [5] можно представить в виде табл. 1.

Таблица 1

Система функций выходов

Table 1

System of functions of outputs

	1
X i( t)	Gl(t) < 1
X 2( t)	^(t) < 1
* 3(0	a3 ( t) > 0

Структурный граф модели изображен на рисунке.

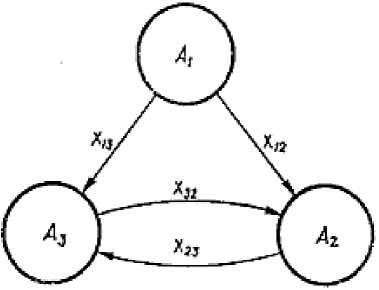
Структурный граф модели

Network diagram of execution of rules of expert system

Матрица а л ф а в итов [ 6] име е т в и д , представленный в табл. 2.

Таблица 2

Матрица алфавитов

Table 2

Matrix of alphabets

P	Д	Д
Θ	Н	Д
Θ	Д	Н

Таб ли ц а у с лов н ых фу н к ц и он а лов п е ре ходов ( Т УФП) , устанавливающая соответствие между в ы с к а зыв а н и ями и фу н к ц и он а ла ми , представлена в следующем виде (табл. 3).

Таблица 3

Таблица условных функционалов переходов

Table 3

Table of conditional functionalities of transitions

Л 1	a1(t) > 1	a1(t) < 1
	Я 1 (t) — 1	5
^ 2	« 2 (t) > 1	a2 (t) < 1Л x1 (t) + %3 (t) > 0	a2(t) < 1 A%1(t) + %2(t) = 0
	a 2 (t) — 1	n	0
^ 2	U1 (t) + %(t)

В к а чес тв е век тора началь ных состояний можно выбрать любые три чи с л а , из к оторы х п е рвое – п о лож и тельн ое ц е л ое , а в торое и тре ть е – натуральные. Исключение представляют лишь так и е три чи с ла, г д е п ри п рои звольном первом второе равно нулю, а третье отли чн о от н у ля. С мысл так ого иск л ю че н ия в п олне ясен: когда в очереди имеются клиенты, об с лу жи в а ющ и й м ех а н изм н е мож е т п рос т а и в а ть [7] .

Поск оль к у в раб оте ра с смотре н ной системы участвуют две независимые случайные величины f и р , т о за да н и е с и с те м ы р аспределений случайных величин может осу щ ес тв лятьс я с п ос обо м блок и р ов к и. Из в с е х в озм ожн ых с п ос о б ов б л ок и ро в к и в ыб е ре м два.

Задание системы распределений случайных величин способом блокировки

Блок ировк а входя ще го по тока т ран зак тов . В каждый момент времени t входящий поток, на кот оры й н е д е й с тв у е т б л ок и ровка, может быть заблокирован в течение проме жу тк а в ре м е н и случайной длительности у с в е роятн ос тью р (0 < р < 1) или не заблокирован с противоположной в ероя тн ос тью. Д ля оп реде ле н н ос ти об озн а чи м че р е з т двоичную случайную величину с распределением [1-р, р}. В моме н т о кончания действия блокировки на вход посту п а е т оч е ре д н ой к лиен т, и да л е е с ис те ма п ро должае т фу н к ц и он и ров ать нормально [8].

Блок ировк а об с лужив ающ его м ех ани зм а . Блокировка (выход из строя) происходит после отр а б отк и об с лу жи в аю щ им ме ха н и змом с лу ча й н о го к о ли че с тв а в рабочих единиц времени [9].

Время простоя в эту величину не входит. После выхода механизма из строя в течение случайного времени а происходит его восстановление (ремонт). Далее продолжается обслуживание транзакта, прерванное в момент выхода механизма из строя.

Найдем математическое ожидание промежутка простоя обслуживающего механизма при отсутствии блокировки (в исправном состоянии). Заметим, что ввиду возможности выхода из строя механизма только в рабочем состоянии каждый из таких промежутков будет заканчиваться лишь при поступлении новых транзактов в систему, но не при прекращении действия блокировки обслуживающего механизма.

Основная часть модели состоит из шести автоматов [10], которые обозначим Л_ъ Л₂,..., Л₆. Автоматы индикатора (их три) обозначим буквой U с соответствующим индексом. Как всегда, построение модели начнем с определения конкретного смысла состояний автоматов.

Положим: а₄ (t) - промежуток времени, оставшийся в момент времени t до момента поступления очередного транзакта; а₂ (t) - промежуток времени, оставшийся от момента t до момента окончания обслуживания очередного транзакта, если в момент t имеется некоторый транзакт, поступивший на обслуживание, независимо от того, является обслуживающий механизм в данный момент исправным или нет, в противном случае a₂(t) = 0; а₃ (t) - количество транзактов, ожидающих обслуживания в момент времени t; n₄(t) - промежуток времени, оставшийся от момента t до момента окончания блокировки входящего потока, если в этот момент действует блокировка, в противном случае a₄(t) = 0; a_s(t) - значение качественной компоненты блокировки обслуживающего механизма в момент времени t, если в этот момент действует блокировка, то a₅(t) = 1, в противном случае a g (t) = 0; a₆(t) - значение количественной компоненты блокировки обслуживающего механизма в момент времени t, т. е. промежуток времени от момента t до момента очередной смены качественного состояния блокировки механизма; и_г (t) - накопленное за промежуток времени от начала функционирования модели до момента t суммарное время простоя обслуживающего механизма в исправном состоянии; u₂(t) - накопленное за этот же промежуток времени суммарное количество промежутков незанятости обслуживающего механизма; u₃ (t) - приближенное значение математического ожидания длительности простоя обслуживающего механизма в исправном состоянии, полученное путем усреднения по промежутку времени (0, t — 1).

Такое задание состояний автоматов дополним следующими замечаниями.

• 1.    Ввиду того, что по принятому условию задачи в момент окончания действия блокировки на входящий поток на вход системы всегда поступает транзакт, при наличии этой блокировки промежуток времени до поступления очередного транзакта определяется состоянием автомата Л₄, а не состоянием автомата Л₄ последнее в рассматриваемом случае теряет смысл и может быть выбрано произвольно [11, с. 203–211].

• 2.    Поскольку по условию задачи предполагается, что в каждый момент времени, когда на входящий поток не действует блокировка, последняя может наступить с одинаковой вероятностью, для описания этой блокировки достаточно выбрать лишь одну временную характеристику. Действительно, эту характеристику можно задать так: в момент действия блокировки она совпадает со значением промежутка времени, оставшегося до окончания действия блокировки, в противном случае равна нулю [12]. В качестве этой компоненты в модели фигурирует состояние автомата Л₄. С блокировкой обслуживающего механизма дело обстоит совершенно иначе. Состояние блокировки и состояние ее отсутствия наступают или не наступают в зависимости от того, сколько времени прошло с момента наступления или окончания блокировки, поэтому для полного описания блокировки обслуживающего механизма необходимо ввести две временные характеристики: качественную и количественную, как это сделано в рассматриваемой модели путем добавления автоматов Л₅ и Л₆.

• 3.    В каждый момент времени обслуживающий механизм может находиться, будучи исправным [13], либо в рабочем состоянии, либо в состоянии простоя, либо быть в неисправном (заблокированном) состоянии. Нас интересуют лишь промежутки времени простоя обслуживающего механизма в исправном состоянии. Такие промежутки могут иметь произвольную целочисленную длительность. В процессе функционирования модели автомат U_T является накопителем количества единиц времени, когда обслуживающий механизм простаивал в исправном состоянии, а автомат U₂ - числа промежутков времени непрерывного нахождения механизма в этом состоянии.

Из условия задачи пока не ясно, как должен действовать транзакт, который прибыл в момент, когда обслуживающий механизм был заблокирован и в системе не было ни одного транзакта (в том числе частично обслуженного), т. е. должен ли он находиться в очереди до прекращения действия блокировки или поступить к обслуживающему механизму и продолжать ожидание там. С точки зрения содержания эти два случая неразличимы, так как безразлично, где происходит пассивная задержка [14]. Однако с точки зрения алгоритмического описания модели здесь имеется существенная разница, например для определения состояний автоматов Л2 и Л3. Следовательно, при построении модели необходимо принять одну их этих версий за истину. Будем придерживаться того мнения, что в указанном случае ожидание происходит непосредственно в обслуживающем приборе, а не в очереди [15].

Обозначим выходные сигналы автоматов Л_ъ Л₂,..., Л₆ буквой х с индексом, соответствующим номеру автомата, и указанием на момент времени. Выходные сигналы автоматов индикатора обозначим так же, как внутренние состояния этих автоматов.

Пусть x₁(t) - сигнал, принимающий значение 1 в момент, предшествующий поступлению транзакта на вход системы вследствие естественного течения входящего потока (а не вследствие прекращения блокировки этого потока), и значение 0 - в противном случае; х₂ (t) - сигнал, равный 0, когда в момент t обслуживающий механизм свободен, 1, когда он занят, но освободится через единицу времени, и 2 - в остальных случаях; х₃ (t) - сигнал, равный 1 при наличии в очереди хотя бы одного транзакта и 0 - в противном случае; X₄(t) - сигнал, равный 0, когда блокировка входящего потока отсутствует, 1, когда действие блокировки через единицу времени закончится, и 2 - в остальных случаях; х₅ (t) - сигнал, совпадающий в каждый момент времени с качественной компонентой описания блокировки обслуживающего механизма, т. е. с состоянием автомата Л₅; X₆(t) - сигнал, принимающий значение 1, если до очередной смены качественной компоненты описания этой блокировки остается точно одна единица времени, и значение 0 – в противном случае.

Построим систему функции выходов для двоичных сигналов (табл. 4).

Таблица 4

Система функции выходов для двоичных сигналов Table 4 The system of function of outputs for binary signals

	1
X i (t)	ai(t) = 1
X 3 (t)	a3 ( t) > 0
x s (t)	«sCO = 1
X 6 (t)	«6 to = 1

Для автоматов индикатора функции выходов уже определены путем принятия предположения об их тождественности состояниям соответствующих автоматов. Для упрощения записи ТУФП введем промежуточные величины: y1(t) - величина, равная 1, если в момент времени t + 1 должен поступить транзакт за счет прекращения действия блокировки, и равная 0 - в противном случае; y2(t) - величина, равная 1 в том случае, если в момент времени t + 1 обслуживающий механизм способен принять одного транзакта, включая и тот случай, когда действует блокировка этого механизма, и 0 - в остальных случаях; z (t) - суммарное количество транзактов, находящихся в очереди в момент t либо поступающих в систему в этот момент времени в порядке нормального течения входящего потока или ввиду прекращения действия блокировки.

Для вычисления значений промежуточных величин имеем следующие формулы:

vt 1 =JO y 2 (t) ={0

при X4(t) = 1, при X4(t) ^ 1; при X2(t) = 0 или X2(t) = 1 и X5(t) = 0, при X2(t) = 2 или X2(t) = 1 и X5(t) = 1.                                     ()

Выражение для y2(t), как нетрудно убедиться, можно переписать в более простом виде:

^у2® = !0

приx2(t) + x5(t) < 1, при x2 (t) + xq (t) > 2,

или

y2(t) = 1 — max{0, min{1,x2(t) + xq(t) — 1}}.

ТУФП представляется в виде табл. 5:

Таблица 5 ТУФП

Table 5

TUFP

А 1	«1 > 1 Л x4 = 0		«1 > 1Л x4 = 0 V x4 = 1			x4 = 2
	«1 — 1		5			0
А 2	«2 > 1V «2 = 1Л xq = 1		z > 0Л(«2< 1Лxq = = 0V«2 = 0ЛxR = 1)			z = 0Л(«2< 1Лxq = = 0V«2 = 0ЛxR = 1)
	« 2 + x q — 1		n			0
А 3	max{0, «3 + x1 + у1 — y2}
А 4	«4 > 0				«4 = 0
	« 4 — 1				ту
А 5	«q = 0ЛX2 = 0		«q = 0 Л x2 > 0			« 5 = 1
	0		x 6			1 — x 6
А 6	« 6 > 1Л x5 = = 0V«6>1Vxq = = 0Лx2 > 0	« 6 > 1Л x5 = = 0 Л x2 = 0		« 6 = 1Л x5 = 1			« 6 = 1Л x5 = 1
	« 6 — 1	« 6		в			a
^ 1	u1 + (1 — xq) max{0,1 — x2}
^ 2	z > 0			z = 0
	u2 + max{(0,1 — x2)} (1 — xq)			« 2
^ 3	u1: max{1,u2}

Рассмотрим полученный вариант подробнее.

Автомат А₁. Если в момент t блокировка входящего потока не действует и до поступления очередного транзакта остается промежуток времени, превышающий единицу, то естественно, что состояние автомата за единичный промежуток времени уменьшится на единицу, т. е.

«^t + 1) = «1 (t) — 1 при x4(t) = 0 и «1(t) > 1.                                         (4)

Если в момент t также не было блокировки, но время, оставшееся до поступления транзакта, равно единице, то в следующей момент времени транзакт поступит и до поступления очередного останется случайный промежуток времени, совпадающий с одной из реализаций случайной величины ^.

Совершенно тот же результат будет, если в момент времени t действует блокировка на входящий поток и до окончания ее действия остается одна единица времени (x4(t) = 1) независимо от состояния автомата А1. Если в момент t на входящий поток действует блокировка и до окончания этого действия остается промежуток, превышающий единицу времени, что может случиться тогда и только тогда, когда x4(t) = 2, то на основании сделанного выше замечания состояние автомата А1 можно выбрать произвольно. Это осуществимо при предположении, что «1(t) = 0.

Автомат А₂. Что касается изменения состояния этого автомата, то возможны три результата:

• 1)    состояние автомата уменьшится на величину, противоположную значению сигнала x₅(t), т. е.

«2(t + 1) = «2(t) — (1 — x5(t)) = «2(t) + x5(t) — 1;                                       (5)

• 2)    начнется обслуживание очередного транзакта, т. е. в момент t + 1 состояние автомата совпадает с одной из реализаций случайной величины р;

• 3)    в момент t + 1 обслуживающий механизм попадет в состояние простоя (будучи исправным или нет), т. e. «₂(t + 1) = 0.

Первый из перечисленных результатов возможен в двух случаях: когда до окончания обработки обслуживаемого транзакта остается промежуток, больший одной единицы времени (при наличии или отсутствии блокировки), и когда при наличии блокировки этот промежуток равен единице.

Второй результат имеет место также в двух случаях: когда при отсутствии блокировки остаточное время обслуживания не превышает единицы и в этот момент времени произойдет поступление транзакта, если таковые имеются в очереди (z (t) > 0), а также когда условие z (t) > 0 наличия или поступления клиентов при незанятости обслуживающего прибора (a₂(t) = 0) сопровождается информацией о наличии в момент t (x₃(t) = 1) действия блокировки нa обслуживающий механизм.

Третий, нулевой, результат имеет место тоже в двух случаях: когда при отсутствии блокировки (x₅(t) = 0) и фактической (a₂(t) = 0) или ожидающейся (a₂(t) = 1) незанятости обслуживающего механизма нет возможных претендентов нa обслуживание (z (t) = 0) и когда незанятость механизма и отсутствие заявок на обслуживание сопровождаются наличием в момент t блокировки механизма.

Автомат Л₃. Исходим из основного принципа формирования очереди изложенного выше. В этом случае количество прибываюших транзактов (0 или 1) совпадает со значением суммы x₄ (t) + У (t). В момент вpeмeни t из очереди может убыть (для обслуживания) один транзакт или не убыть ни одного. Эту величину обозначим через y₂(t).

Таким образом, имеем

а3 (t + 1) = max{0, а3 (t) + xx (t) + у4 (t) - У2 (t)}, (6) когда такое убытие происходит.

Автомат Л₄. Если в момент t на входящий поток действует блокировка (a₄(t) > 0), то в последующий момент времени t + 1 ее остаточная длительность уменьшится на единицу, в противном случае в момент t + 1 блокировка будет отсутствовать c вероятностью, равной (1 — р), или с вероятностью р начнется новый блокировочный период, причем его остаточная длительность в этом случае совпадет с одной из реализаций случайной величины у. Следовательно, при a₄(t) = 0 новое состояние автомата Л₄ можно изобразить в виде пpоизведения ту случайных сомножителей т и у.

Автомат Л₅. Если в момент t на обслуживающий механизм блокировка не действует (п₅ (t) = 0) и этот механизм свободен (х₂ (t) = 0), то естественно, что в момент времени t + 1 блокировки также не будет. Если при отсутствии блокировки в момент t и занятости обслуживающего механизма остаточное время безблокировочного периода равно единице (x₆(t) = 1), то в момент t + 1 наступит новый период блокирования. Если же при этом остаточное безблокиро-вочное время больше единицы (x₆(t) > 1), то блокировка не наступает. В этом случае повое состояние автомата Л₅ можно записать так: a₅(t + 1) = x₆(t).

Если в момент t действует блокировка обслуживания (а₅ (t) = 1), то состояние автомата Л₅ в момент t + 1 примет значение, противоположное значению сигнала x₆(t), т. е. a₅(t + 1) = = 1 — X 6 (t).

Автомат А₆. Рассмотрим случай, когда состояние автомата не изменяется. Очевидно, что это происходит только тогда, когда в момент t отсутствует блокировка обслуживания (x₅(t) = 0), обслуживающий механизм простаивает (x₂(t) = 0) и остаточная часть безблокировочного периода больше или равна единице. Следовательно, a₆(t + 1) = а₆.

В двух остальных случаях состояние автомата может уменьшиться на единицу. Эти случаи такие:

• 1)    блокировка обслуживания имеет место (x₅(t) = 1) и остаточное время блокировочного периода превышает единицу;

• 2)    блокировка не действует (x₅ (t) = 0), обслуживающий механизм занят (x₂ (t) > 0) и остаточный безблокировочный период превышает единицу.

Если в момент t блокировка механизма имеет место и ее остаточная длительность равна единице, то в следующий момент времени t + 1 наступает безблокировочный период и его остаточная длительность совпадает с одной из реализаций случайной величины а.

При отсутствии блокировки (x5(t) = 0), занятости механизма (x2(t) > 0) и остаточном без- блокировочном времени, равном единице, в момент t + 1 начинается блокировка и ее остаточное время совпадает с реализацией случайной величины а.

Автомат U. На основании определения состояние этого автомата должно увеличиваться на единицу лишь тогда, когда обслуживающий механизм простаивает, не будучи заблокирован, т. е. добавления единицы к u_T(t) не происходит, когда действует блокировка (x₅(t) = 1) или обслуживающий механизм занят (х₂ (t) > 0). Это можно учесть, прибавляя к «старому» состоянию автомата такое выражение, зависящее от х₂ и х₅, которое равно единице во всех случаях, кроме указанных. Нетрудно увидеть, что именно таким выражением является произведение

• (1    — х₅ (t)) max ^{ 0,1 - Х 2 (t) ^} .                                                               (7)

Автомат U2. По определению состояние этого автомата в момент времени t должно совпадать с количеством промежутков незанятости обслуживающего механизма при отсутствии блокировки. Такие промежутки можно подсчитывать либо по их началам, либо по их концам. Выберем последний способ. Следовательно, функционал для определения u2(t) должен быть составлен так, чтобы он подсчитывал количество переходов обслуживающего механизма из состояния простоя при исправности этого механизма в какое-либо другое состояние. Очевидно, что, если в момент t имеются транзакты, которые либо находятся в очереди, либо поступают в систему извне по той или другой причине, т. е. когда z (t) = 0, интересующий нас переход произойти не может и единица к u2 (t) не прибавляется. В противном случае (z (t) > 0) к u2 (t) единица прибавляется тогда и только тогда, когда механизм простаивает (x2(t) = 0) и блокировки нет (x5(t) = 0). Имеем u2(t + 1) = u2(t) + max{0,1 — x2(t) } (1 — x5(t)).                                          (8)

Автомат U₃. Вычислить приближенное значение математического ожидания периода простоя механизма в исправном (незаблокированном) состоянии можно, разделив суммарное время пребывания механизма в этом состоянии за какой-то достаточно большой промежуток времени Г на количество промежутков непрерывного пребывания его в исправном состоянии за тот же период времени Г. Чтобы в начале машинной реализации функционирования модели, когда еще u₂(t) = 0, не происходило автоматической остановки при делении на нуль, применяем символ max.

Начальное состояние автоматов индикатора – нулевое. Для остальных автоматов можно выбрать произвольные начальные состояния, соответствующие реально возможной ситуации.

Заключение

Таким образом, схема решения задачи с помощью построенной автоматной модели такова. Прежде всего принимают решение, по какому показателю, в данном случае в свете требований решаемой задачи, целесообразно судить об эффективности работы информационной системы. После этого решается вопрос о том, за счет чего, за счет какого изменения режима работы системы, ее структуры или значений параметров можно добиться максимальной эффективности. Речь идет о выборе совокупности регулируемых параметров или совокупности испытываемых вариантов. Показатель эффективности работы системы является детерминированной функцией регулируемых параметров. Эта функция называется целевой или критерием эффективности системы. Вид целевой функции до начала исследования неизвестен. В противном случае не потребовалось бы применение имитационных методов. Решение любой задачи имитационного моделирования заключается в том, чтобы из заданного множества значений совокупности регулируемых параметров выбрать такую совокупность этих значений, при которой целевая функция принимает минимальное (максимальное) значение.