Моделирование биогеохимических процессов в Азовском море с использованием статистически обработанных данных о речном стоке

Funding information: the research is done with the financial support from RFFI (project no. 20-01-00421).

Введение. Азовское море — крупная прибрежная система эстуарного типа. Это самое мелкое море в мире. Оно почти равномерно прогревается летом (с перепадами температуры в среднем не более 4 °С). При этом характеризуется большим перепадом солености — от 0 ‰ до 12–15 ‰, т. к. стоки рек обеспечивают приток пресной воды, соизмеримый с общим объемом вод моря, а из Черного моря в районе Керченского пролива поступает соленая черноморская вода. Речной сток существенно влияет на биохимический состав водоема [1]. Представляется актуальным математическое моделирование биогеохимических процессов, позволяющее проводить диагностические и прогностические расчеты динамики экосистемы моря. Изменчивый по объему и по гидрохимическому составу речной сток заметно влияет на параметры гидрофизических и биологических процессов, происходящих в прибрежной системе. Поэтому целесообразно провести статистический анализ данных многолетних наблюдений, в частности гидрохимических показателей стока рек, впадающих в Азовское море, и на основе статистически обработанных входных данных выполнить прогнозирование биогеохимических процессов.

В области исследования гидродинамики и прогнозирования морских систем следует отметить работы Марчука Г. И. [2], Матишова Г. Г., Сухинова А. И. [3], Бердникова С. В., Тютюнова Ю. В. [4], Якушева Е. В. [5], Ильичева В. Г. и др. В статье представлены результаты комплексирования математической модели биогеохимических циклов с моделью гидродинамики Азовского моря [6–8]. Это позволяет повысить точность моделирования и учесть такие факторы, как гидродинамические процессы в прибрежных системах, неоднородное распределение температур, соленостей и биогенных веществ, влияющих на развитие фитопланктонных популяций, переход биогенов из одной формы в другую [9]. Следует заметить, что численные модели пространственно-трехмерных гидрофизических процессов в прибрежных системах являются предметом отдельного исследования авторского коллектива. Они дают возможность учесть динамически изменяющуюся геометрию дна и береговой линии, ветровое напряжение на свободной поверхности и ее возвышение, трение о дно, силу Кориолиса, турбулентный обмен, испарение, речные стоки, отклонение значений давления в водной среде от гидростатического приближения и др. В представленной работе входные данные (распределение трехмерного вектора скоростей, а также соленостей и температур) являются результатами численных расчетов на основе гидрофизической модели [10].

Материалы и методы. Для описания модели формулируется начально-краевая задача для системы уравнений параболического типа с младшими производными и нелинейными функциями правых частей:

+ u^ + v^ + w^ = d.iv(kgradq( ) + R_q,,                         (1)

at ax ay az          h 4U                                        v '

где qi — концентрация i- й компоненты [мг/л]; i e M , M = { F i , F 2 , F 3 , PO 4 , POP, DOP, NO 3 , NO 2 , NH 4 , Si }; { u,v, w } — компоненты вектора скорости водного потока [м/с]; к — коэффициент турбулентного обмена [м²/с]; R_qi — функция — источник биогенных веществ [мг/(л-с)].

В уравнении (1) индекс i указывает на вид субстанции (таблица 1).

Биогенные вещества в модели динамики фитопланктона

Таблица 1

Номер	Обозначение	Название
1	F 1	Зеленая водоросль Chlorella vulgaris
2	F 2	Сине-зеленая водоросль Aphanizomenon flos-aquae
3	F 3	Диатомовая водоросль Sceletonema costatum
4	PO 4	Фосфаты
5	POP	Взвешенный органический фосфор
6	DOP	Растворенный органический фосфор
7	NO 3	Нитраты
8	NO 2	Нитриты
9	NH 4	Аммоний
10	Si	Растворенный неорганический кремний (кремниевые кислоты)

Химико-биологические источники описаны следующими уравнениями ( i e { 1,2,3 } , где 1 — это ChV, 2 — AF - A , 3 — Sc , а ChV, AF - A, Sc — символические обозначения видов планктона):

RPOP = SSpKFDqF — KPDqPOP — KPNqPOP , i=1              ‘           ‘

Информатика, вычислительная техника и управление

^R DOP = ^S S P K FEqF ⁺ K PD q POP ^— KD N q DOP , i =1

R PO 4

= S s p C F; ( K FR ^{— 1} ) q Fi ⁺ K PN q POP ⁺ KDN q DOP ,

R NH 4 = ^S s N C F , ( ^K FR

—1)

N ( q NH 4 )

^f N ⁽ q NO 3 ,q NO ₂ ,q NH 4 )

qF_: ^{+ S} ^n ( ^Kfd ^{+ K}f._e ) ^q F.

^^^^^^B

K 42 q NH ₄ ,

R no, = S s N C F (К i =1

—

^f® (, q NO 3 ,q NO2 , q NH 4 )      q NO2     „ ,      „

¹⁾ Z* /                  \          I q Fi ⁺ K 42 q NH 4

f N ⁽ q NO3 ,q NO2 ,q NH 4 ) q NO 2 ⁺ q NO3

^^^^^^B

K 23 q NO ₂ ,

R nO 3 = S S n C , ( К,. — 1 ) i =1

Ум ⁽ q NO 3 , q NO2 , q NH 4 )       q NO 3

-------------,-------------------------------------------Г- • ------------------------- fN ( qNC3 ,qNO2 ,q NH4 )  qNO + q i

— q„ + K^.q ,

F _i 23 NO ₂ , NO 3

R_s = sC К К —- 1 q_R + s_4iK_Frq . S S F 3 F 3 R         F 3 S F ₃ D F 3

Здесь K_FR — удельная скорость дыхания фитопланктона; K_FD — удельная скорость отмирания фитопланктона; K_FE — удельная скорость экскреции фитопланктона; K_PD — удельная скорость автолиза РОР ; K_PN — коэффициент фосфатофикации РОР ; K_DN — коэффициент фосфатофикации DОР ; K ₄₂ — удельная скорость окисления аммония до нитритов в процессе нитрификации; K ₂₃ — удельная скорость окисления нитритов до нитратов в процессе нитрификации; s_P , s_N , s_S — нормировочные коэффициенты между содержанием N , P , S в органическом веществе [11–12].

Скорость роста фитопланктона определяется выражениями c^ = KN,^ fT (T) fs (S) m n {fp (q„o4) f (qKO3 ,qHO2 ^4)}, сз=К fi (T) fs (S) m in {fP (qpo4), fN (q3 ,q«O2 -q.4), fs (q®)}, где KNF — максимальная удельная скорость роста фитопланктона.

Зависимости температуры и солености:

f T ⁽ T ) = exp — а

T-T 1 opt \

I opt 7

, f s ⁽ s ) = exp —в

2 s — S op. ) S op. )

,

где T op. , S_opt — температура и соленость, оптимальные для данного вида фитопланктона; а >  0 , в >  0 —

коэффициенты ширины интервала толерантности фитопланктона к температуре и солености соответственно.

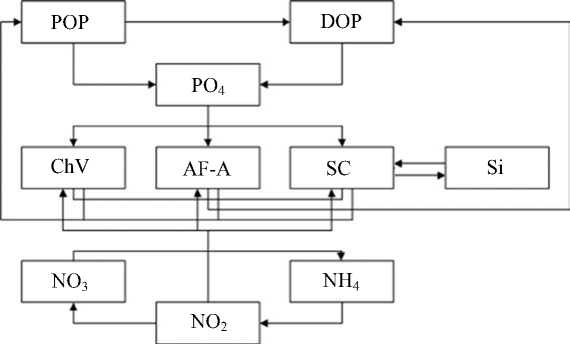
Рис. 1. Модельная схема биогеохимической трансформации форм фосфора, азота и кремния

Ниже представлены функции, описывающие содержание биогенов.

^q PO

Для фосфора f_p ( q ) =-----⁴---, где K — константа полунасыщения фосфатами.

O^™ 4' q pO 4 + K po 4          ^PO 4

Для кремния f ( q_s ) = —^qs‘— , где К — константа полунасыщения кремнием. ^s‘^' q_s + K_S i        ^s

Для азота f N ( q NO3 , q NO^ , q NH4 ) = f N ¹* ( q NO, , q NO, , q NH 4 ) + ^f^ ( q NH 4 ) ,

f N^{1 (} q NO 3 ,q NO 2 , q NH 4 ) =

⁽ q NO 3 + q NO, )exp^{( —} K ps. q NH ₄ )

K NO 3 ^{+ ( q} NO 3 ^{+ q} NO 2 )

f ⁽²⁾           ____ q NH ¹_____

, JN ⁽ q NH 4)    _K

K NH 4 ⁺ q NH 4

где K_NO — константа полунасыщения нитратами; K_NH — константа полунасыщения аммонием; K_psi — коэффициент ингибирования аммония.

Предположим, что коэффициенты, входящие в выражения для функций источников, положительны и не зависят от времени t .

Для системы (1) ставится начально-краевая задача в цилиндрической области G . Пусть граница S цилиндрической области G является кусочно-гладкой поверхностью и S = S _H uS _o и о , где S _H — поверхность дна водоема, S _o — невозмущенная поверхность водной среды, о — боковая (цилиндрическая) поверхность.

Пусть u n — нормальная по отношению к S составляющая вектора скорости водного потока, n — вектор внешней нормали к S . Допустим для концентраций qi на боковой границе:

qi = 0, на о, если un < 0, i еM;(2)

д q

—i- = 0, на о, если un > 0, iеM;(3)

д n д q

— = 0, на S — поверхность водоема, i еM;(4)

дz д q

• — = ^£^, i ^{е {} F i , F 2 , F 3 }, — = £ ^i q i ;

дzд iе {PO4, POP, DOP, NO3, NO2, NH4, Si} на дне SH.(5)

Здесь £_u, £_2i — неотрицательные постоянные; £_u, i e { F 1 , F ₂, F ₃} учитывают опускание водорослей на дно и их затопление; £ ₂ i, i е { PO ₄, POP, DOP, NO ₃, NO ₂, NH ₄, Si } учитывают поглощение питательных веществ донными отложениями.

Для системы уравнений необходимо в любой момент времени задавать вектор скоростей водного потока, поле солености и температуры, а также начальные значения функций q_i :

q i ( X , y , z ,0 ) = q 0 i -( X , y , z ) , ( X , y , z ) e G , t = 0, i е M ,                                   (6)

• V ( x , У , z ,0 ) = V ( x , У , z ) , T ( x , У , z ,0 ) = T 0 ( x , У , z ) , S ( x , У , z ,0 ) = S 0 ( x , У , z ) ^.

Статистическая обработка данных многолетних наблюдений о стоках рек в Азовское море. Значительный относительно объемов моря речной сток существенно влияет на биологические и гидрофизические процессы, происходящие в Азовском море [13]. Со стоками рек в водоем поступает большое количество биогенных веществ, в том числе азота, фосфора и кремния — основных питательных элементов для фитопланктона. В ХХ веке основная часть притока вод в Азовское море приходится на сток Дона — 63 % (рис. 2–4)¹.

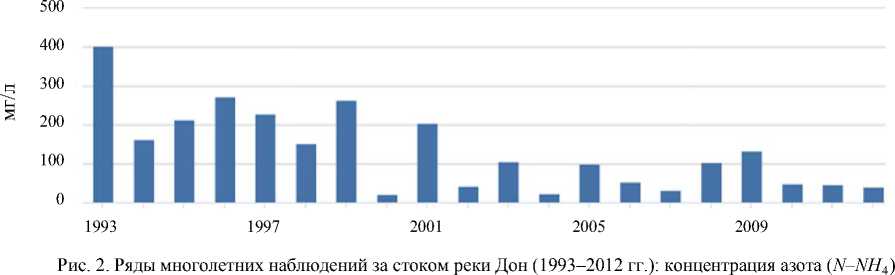
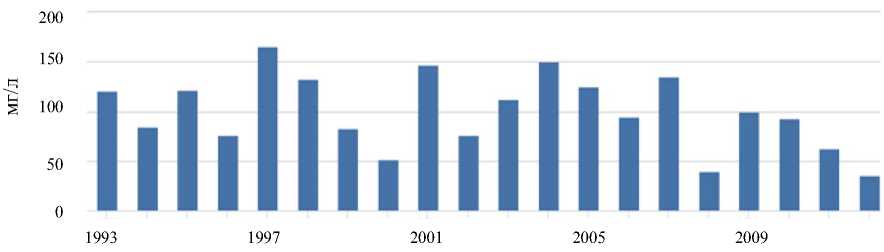
Рис. 3. Ряды многолетних наблюдений за стоком реки Дон (1993–2012 гг.): концентрация фосфора ( PO ₄)

Информатика, вычислительная техника и управление

Lhllllilllllllllll

1993                1997                2001                2005                2009

Рис. 4. Ряды многолетних наблюдений за стоком реки Дон (1993–2012 гг.): концентрация кремния ( SiO ₄)

Таблица 2

Результаты расчета статистических параметров данных натурных наблюдений

Показатель N-NH4 PO4 SiO4 Количество значений 20 20 20 Максимальное значение 403,9 165,0 4166,7 Минимальное значение 20,6 35,4 287,3 Среднее арифметическое значение 132,3 100,1 2648,1 Дисперсия 10362,5 1309,0 868441,9 Стандартное отклонение 101,8 36,2 931,9 Коэффициент асимметрии Cs 0,9 –0,1 –0,7 Коэффициент эксцесса Ce 0,2 –0,9 0,2 Коэффициент вариации Cv 0,8 0,4 0,4 Отношение Cs/Cv 1,2 –0,3 –2,0 Коэффициент автокорреляции 0,3 –0,1 0,1 Отношение Неймана 1,1 2,0 1,8

Исследование рядов многолетних наблюдений за стоком Дона позволяет сделать ряд выводов.

— Рассматриваемые концентрации питательных веществ обладают как положительной, так и отрицательной асимметрией.

— Случайные величины для азота и кремния смещены относительно центра распределения, о чем свидетельствует высокое значение коэффициента асимметрии.

— Большие значения дисперсий и среднеквадратических отклонений получены для всех биогенов.

— Коэффициенты автокорреляции малы, следовательно, для рядов натурных данных характерна сильная нелинейная тенденция.

— Вариация во всех рядах больше 20 %, следовательно, ряды сильно вариативны.

— Для азота очевидно наличие автокорреляционной связи по критерию Андерсона при количестве значений в выборке 20, так как коэффициент автокорреляции превышает 0,299 при уровне значимости 5%.

— Для азота очевидно наличие автокорреляции остатков по критерию Неймана при уровне значимости 5% для 20 наблюдений, т. к. отношение Неймана меньше 1,2.

— Фосфор и кремний не демонстрируют автокорреляционные связи, гипотезу об автокорреляции остатков отвергаем.

В результате статистического анализа натурных данных [14] можно сделать вывод об их сильной изменчивости. Это обусловлено стохастичностью поступления биогенных веществ со стоком Дона и существенно меняющимся объемом стока под воздействием природных и антропогенных факторов. Для использования натурных данных в модели (1)–(6) целесообразно учитывать сезонные изменения. Далее при моделировании будем рассматривать летний период.

Результаты численных экспериментов. Проведено численное моделирование решения задачи динамики фитопланктонных популяций в летнее время с учетом трансформации форм фосфора, азота и кремния на примере Азовского моря. Моделируемая область соответствует физическим размерам Азовского моря: длина — 355 км, ширина — 233 км, шаг по пространству в горизонтальных направлениях — 1000 м. На рис. 5 приведен спутниковый снимок Азовского моря, подтверждающий соответствие результатов работы натурным данным. На снимке отчетливо видны распределения зеленых и сине-зеленых водорослей в области Таганрогского залива и диатомовых водорослей — в центральной части моря.

Рис. 5. Спутниковый снимок Азовского моря, сделанный с помощью спектрорадиометра с умеренным разрешением (MODIS) спутником NASA Aqua 31 июля 2004 года

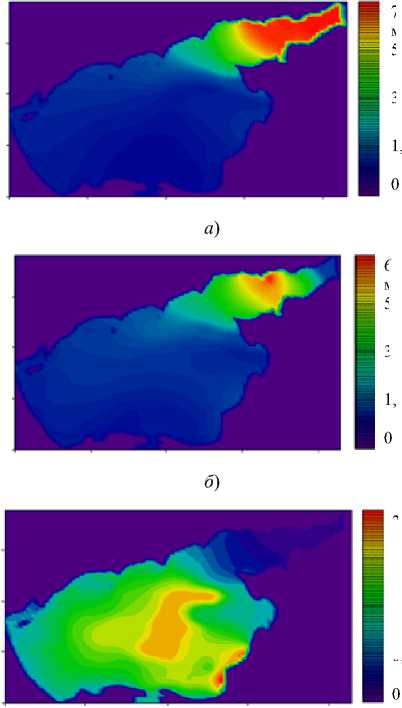
В результате вычислительного эксперимента получены сеточные распределения концентраций основных популяций фитопланктона и питательных веществ в Азовском море (рис. 6). Период расчета — 30 суток. Этого достаточно для установления стационарных режимов в задачах динамики фитопланктона.

3,862

1,931

3,442

1,721

1,284

0,642

6.884 мг/л 5.163

2.569 мг/л 1.927

7.725 мг/л 5.793

в)

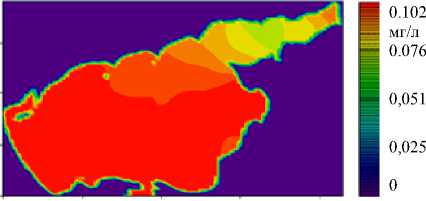
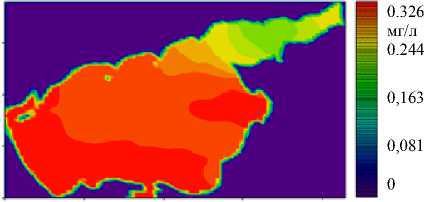
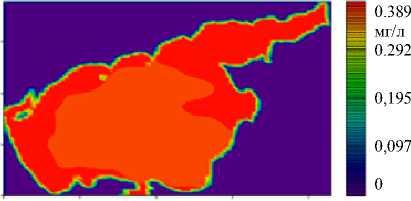
е)

Рис. 6. Распределения концентраций: зеленой водоросли Chlorella vulgaris ( а ); сине-зеленой водоросли Aphanizomenon flos-aquae ( б ); диатомовой водоросли Sceletonema costatum ( в ); фосфатов ( г ); нитратов ( д );

растворенного неорганического кремния ( е )

Рисунки отражают динамику фитопланктонных популяций, циклы фосфора, азота и кремния. В процессе экскреции и отмирания фитопланктон выделяет фосфор в растворенной и взвешенной органических формах, затем в процессе фосфатофикации они переходят в неорганическую форму — фосфаты, которые потребляет фитопланктон. Также описан цикл азота: в процессе жизнедеятельности фитопланктон выделяет азот в органическом виде, который разлагается до аммиака. Аммиак в процессе нитрификации окисляется до нитритов, а затем до нитратов. Стоит отметить, что фитопланктон потребляет все три формы азота. Отмечено потребление и выделение кремния диатомовыми водорослями. Сравнение с результатами моделирования для многоводных периодов показывает, что в последние маловодные годы ареалы обитания зеленых и сине-

Информатика, вычислительная техника и управление

зеленых водорослей в области Таганрогского залива существенно (на многие километры) сместились в восточном направлении, ближе к Дону — источнику пресной воды.

Обсуждение и заключения. В работе приведена многовидовая математическая модель динамики фитопланктонных популяций, трансформаций форм биогенных веществ — соединений фосфора, азота, кремния. В модели учтено:

• —    влияние солености и температуры на развитие трех основных видов фитопланктона (зеленых, синезеленых и диатомовых водорослей);

• —    поглощение фитопланктоном фосфатов и форм азота,

• —    переход форм фосфора и азота из одной в другую,

• —    поглощение кремния диатомовыми водорослями,

• —    адвективное и микротурбулентное движение водной среды,

• —    стоки и источники на границе.

Для анализа натурных данных разработана и адаптирована методика статистического анализа многолетних рядов наблюдений концентраций биогенных веществ (фосфора, азота, их соединений и др.), которые поступают в море со стоком Дона. Статистический анализ данных многолетних наблюдений, в частности гидрохимических показателей стока Дона, стал базой для прогнозирования биогеохимических процессов с учетом движения водной среды, распределения температур и солености. Результаты численных экспериментов согласуются с данными космического зондирования Азовского моря, что является подтверждением предсказательной ценности применяемых моделей и методов их численной реализации. Сравнение распределений популяций зеленых и сине-зеленых водорослей в Таганрогском заливе для многоводных и маловодных периодов показывает, что ареалы их обитания в последние маловодные годы существенно (на многие километры) сместились в восточном направлении, ближе к Дону — источнику пресной воды.