Моделирование деформирования плоских конструкций со сложными криволинейными структурами армирования

Для безопасной работы конструкций с концентраторами напряжений, в окрестности которых возникают большие градиенты полей напряжений, что часто встречается в авиационных конструкциях, их армируют высокопрочными волокнами с целью воспри- ятия волокнами этих градиентов. Но волокна могут и не выполнить эту роль, тогда нагрузка будет влиять на связующее. До последнего времени армирование плоских конструкций осуществлялось прямолинейными волокнами. Однако такая структура армирова- ния может быть эффективной лишь в частных случаях нагружения, при которых внутренние силовые потоки преимущественно направлены вдоль траекторий армирования. Реальные конструктивные элементы работают в более сложных условиях нагружения. Для таких конструкций нужно вводить специальные структуры армирования, которые в определенной мере были бы согласованы с характером полей градиентов напряжений, проводить поиск структур армирования, которые снижают нагрузки, действующие на конструкцию.

На основе структурной модели [1] в работах [2–6] рассмотрены сложные структуры армирования по криволинейным ортогональным траекториям.

Влияние сложного нагружения на распределение силовых линий полей напряжений иллюстрирует следующая задача об эксцентрическом кольце. В данной работе на основе представления решения в виде тригонометрического ряда [7] по криволинейным координатам биполярной системы ( ^ , п )получены следующие результаты для неравномерно нагруженного эксцентрического кольца. Для неравномерной нагрузки на граничном контуре вида const + cos а * п ( а * - заданная амплитуда) контурные графики для компонент напряжений а , о_п , а ^ _п в биполярной системе координат приведены на рис. 1–3.

Многообразие структур армирования на базе ортогональной системы координат достигается построением изогональных траекторий к данным координатным линиям. Детерминантным методом в каждом случае устанавливается тип разрешающих систем дифференциальных уравнений, ставится соответствующая краевая задача.

Определение изогональных траекторий. Изогональная траектория – это плоская линия, пересекающая все кривые заданного на плоскости однопараметрического семейства под одним и тем же углом а . Углы Р 1 и в наклона траектории и кривой к оси OX связаны соотношением в 1 = в ± а.

Если однопараметрическое семейство плоских кривых задано в виде уравнения

F (x, y, a) = 0, (1) (где a – параметр), то изогональные траектории строятся из уравнения дF (x1, y1, a) dy1 дF (x1, y1, a) дy1      dx1        дx1

д F ( x 1 , y 1 , a ) д F ( x 1 , y 1 , a ) dy 1

д y 1              д x 1       dx 1

где k = tg а - известное значение; а - фиксированный угол, под которым изогональная траектория пересекает все кривые заданного на плоскости однопараметрического семейства. Исключая a из двух последних уравнений, получим соотношение, связывающее координаты x ₁, y ₁ точки изогональной траектории и угловой коэффициент касательной k , т. е. дифференциальное уравнение изогональных траекторий семейства (1). Общий интеграл полученного уравнения дает семейство от одного параметра изогональных траекторий [8].

Рассмотрим примеры построения изогональных траекторий к данным координатным линиям.

• 1.    В биполярной системе координат ( £, п ) координатные линии ^ = ^ ₀ = const представляют собой эксцентрические окружности с центрами на оси OX :

⁽ x ^- a cth^ о ) 2 ⁺ y 2 = . , , , ₂ . (shξ ₀)²

Координатные линии п = п _о = const — дуги окружностей с центрами на оси OY и проходящие через две точки x = ± a (полюсы):

22a x +(y + a ctg По) =—-----у.           (4)

(sin η0)2

После введения соответствующей каждому из уравнений (3), (4) линейной замены координат приведем их к уравнению однопараметрического семейства окружностей вида x2 + y2 - b2 = 0, где b – параметр семейства, переобозначения координат не проводим. Для данного уравнения построим семейство изогональных траекторий, следуя (2) [8]. Получим для точек x1, y1, лежащих на траектории, дифференциальное уравнение dyi + xy dx1   y1

k .

• 1    - x y dy i

y ₁ dx ₁

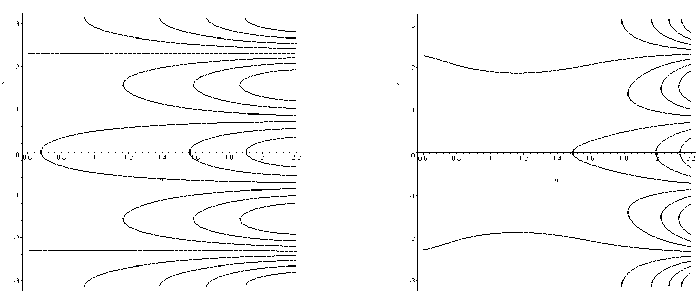
Рис. 1

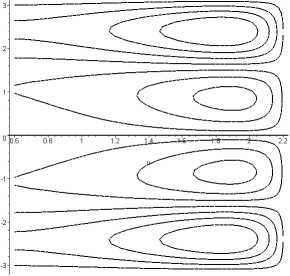
Рис. 3

Рис. 2

После преобразований уравнение (5) запишем как однородное дифференциальное уравнение, его решение имеет вид

собом дифференциальное уравнение изогональных траекторий

Cx ₁ ² +y ₁ ²

x k arctg 1

y

= e ¹ ,

^x 1 У 1 ⁽ У 1 ' ^{- к )2 + (} У 1 ' ^{- к )(} М ⁺ 1) ^{х х ( x}1 ^- У 2 ^- a ²) ^{- x} 1 У 1 ⁽ kV i ^{+ 1)2} = °.

где С – произвольная константа. Каждому семейству окружностей соответствует свое семейство изогональных траекторий в виде семейства спиралей (6).

2. В эллиптической системе координат координатными линиями являются £ -эллипсы и п -гиперболы:

Разрешая (11) относительно у ’ , получим два дифференциальных уравнения первого порядка. Представим его форму после ввода промежуточных обозначений. Пусть

xyx

—2—2--+ 2 2— = 1 и —-— a2ch2 £ a2sh2 £      a2 cos2 п

= 1 , (7) a sin п

где 2 a – фокусное расстояние. Связь между декартовыми ( x , у ) и эллиптическими координатами ( £, п ) дается формулами

S 1 = - к ² + x 1 ² - у ² - a ² + к ² у ² + a ² к ² - 4 x 1 у 1 ,

S 2 = a ⁴ - 2 ax 1 ² + к ⁴ x 4 + 2 к ² x 4 - 2 ak ⁴ x 1 ² + 2 x 1 ² у - + 42  44   42   222   422

+ 2 у 1 к + к у 1 + 2 ak у 1 + 4 к x 1 у 1 + 2 к x 1 у 1 + 4  4  222  222   22   42  4

+ x 1 + у 1 + a к у 1 - a к x 1 + 2 a у 1 + 2 a к + a ,

тогда искомые уравнения запишем в виде

x = a ch £ cos п , у = a sh ^ sin п .          (8)

Запишем (7) как однопараметрическое семейство кривых и построим, следуя (2), соответствующее семейство изогональных траекторий. Введем параметр b ² = a ² ch £ , тогда однопараметрическое семейство

_________ S 1 ± V S 2 _________ 2( ку 1 + a ² к + x 1 у 1 к ² - x 1 у 1 - kx 2 )

запишем в виде

22 xy и - + L-    - b b - a

= 1 .

Семейство изогональных траекторий проще находить, если известно дифференциальное уравнение исходного однопараметрического семейства кривых. Чтобы получить дифференциальное уравнение заданного семейства плоских кривых, необходимо продифференцировать (7), затем из полученного уравнения и уравнения семейства исключить параметр b. В итоге получим дифференциальное уравнение семейства xy (У')2 + У'(x2 - У2 - a2) - ху = 0. (10)

При рассмотрении семейства гипербол его дифференциальное уравнение совпадает с (10), но при этом параметры плоских кривых удовлетворяют условию a ² <  b ² - a ² <  0 [8]. Для семейств эллипсов и гипербол получим в соответствии с изложенным выше спо-

Иллюстрации изогональных траекторий к рассмотренным семействам эллипсов представлены

п

на рис. 4 ( к = 1) для a = , к = tga . Из вида уравне-4

ния (12) следует, что при построении изогональных траекторий могут возникнуть зоны сингулярности для определенных значений k и размеров плоской конструкции. При технологическом конструировании изделий всегда можно выбрать соответствующие размеры вне зоны сингулярности. Иллюстрации изогональных траекторий к рассмотренным семействам гипербол приведены на рис. 5-6 для к = 1 и к = 0,1 соответственно. Пример изогональных траекторий к семейству парабол вида у = ax ² показан на рис. 7 для к = 3.

Как видим, уравнения изогональных траекторий содержат параметр к , при изменении значения которого имеем множество разнообразных траекторий. Располагая армирующие семейства волокон вдоль найденных траекторий, получаем разнообразную структуру армирования, при управлении которой можно перераспределять поля напряжений и деформаций внутри пластины.

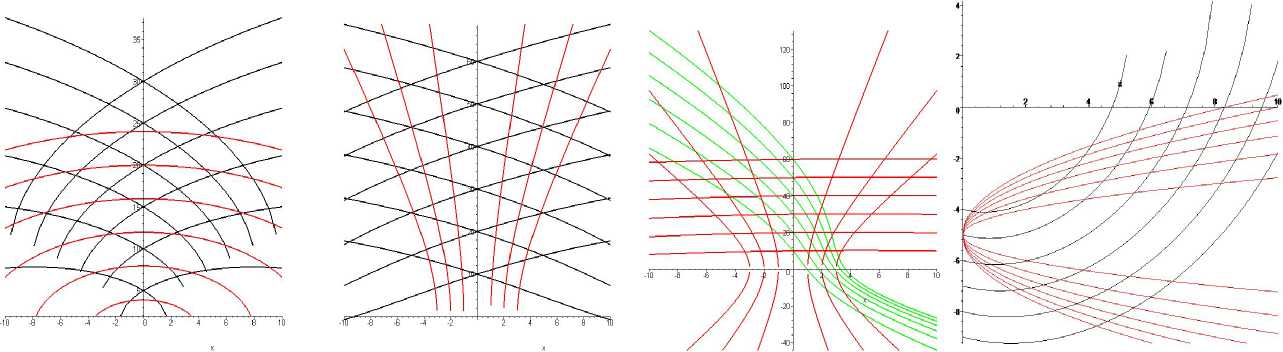
Рис. 4                          Рис. 5                            Рис. 6                          Рис. 7

Изогональные траектории в полярной системе координат. Пусть задана полярная система координат (ρ , θ ). Запишем соотношение (2), отражающее геометрическое определение изогональных траекторий, связывающее направления траекторий и направления семейства, в полярной системе координат. Учтем, что тангенс угла μ между полярным радиусом и касательной в фиксированной точке для любой линии, заданной уравнением ρ = ρ(θ) в полярных координатах, запишется как tgμ= ρ . Последняя формула вы-ρ′ ражает геометрический смысл производной функции ρ = ρ(θ). Тогда соотношение (2), соответствующее полярной системе координат, запишем в виде

k ρ1 + 1 ′

^ρ′ = ^{ρ 1}     ,                    (13)

ρ     ρ1 - 1

ρ1

где k = tgα , α ≠ π/2 – постоянный угол, под которым данное семейство пересекается семейством изогональных траекторий.

Рассмотрим уравнение однопараметрического семейства кривых в полярной системе координат Φ(ρ,θ,a)=0. Чтобы построить изогональные траектории, нужно составить дифференциальное уравнение dρ семейства, затем заменить в нем ρ′ = d θ на производные по формуле (13). В результате получим дифференциальное уравнение для определения изогональной траектории в полярной системе координат. Когда ρ2

α = π/2 , то производная ρ′ заменяется на -     (осу-

ρ′

ществляется предельный переход в (13) при k →∞ ).

Пример 1. Рассмотрим пример построения семейства изогональных траекторий к семейству кардиоид. Пусть задано семейство кардиоид в полярной системе координат:

ρ=a(1 +cos θ), где a – параметр. Дифференцируем уравнение семейства по θ, из полученного уравнения и уравнения семейства исключаем параметр a , находим искомое дифференциальное уравнение семейства

ρ′ (1 + cos θ ) +ρ sin θ= 0 .            (14)

Заменим в (14) производные по формуле (13), индексы опускаем, получим уравнение для изогональных траекторий ρ′ (1 + cos θ- k sin θ ) +ρ ( k + sin θ+ k cos θ ) = 0 .

Интеграл данного уравнения удается найти в аналитическом виде:

ρ ( θ ) = C ( k ²cos θ- cos θ+ 2 k sin θ- k ² - 1) .

В случае k = tg a кривые, пересекающие заданное семейство кардиоид под углом a , задаются уравнением

ρ ( θ ) = a (1 + cos( θ - 2 a )) .

Семейство кардиоид и изогональные ему траектории, пересекающие кривые данного семейства под углом α =^π 4 , изображены на рис. 8.

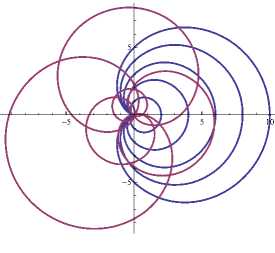
Рис. 8

Пример 2. Рассмотрим семейство логарифмических спиралей ρ ( θ ) = ae ^θ . Дифференциальное уравнение семейства: ρ′ =ρ. Изогональные траектории найдем, решив уравнение (13) для фиксированных значений k , при k = 1 решение этого уравнения ρ = const , т. е. заданное семейство спиралей под углом ^π пересекает семейство концентрических ок-4

ружностей с центром в начале координат (рис. 9).

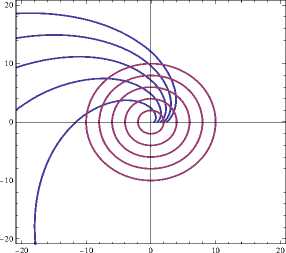
Рис. 9

Пример 3. Введем специальную структуру армирования: прямолинейные радиальные направления. Это пучок прямых с центром в начале координат. Пусть тангенс угла пересечения семейства прямых изогональными траекториями равен k = tg α, причем ^π

α ≠2 . Уравнение изогональных траекторий к данному семейству в полярной системе координат дает θ семейство логарифмических спиралей вида ρ =Cek , где С – произвольная константа.

Множество структур армирования на основе выбранного прямолинейного радиального направления представлено на рис. 10–12 для значений k = 1 , 2 , 3 соответственно.

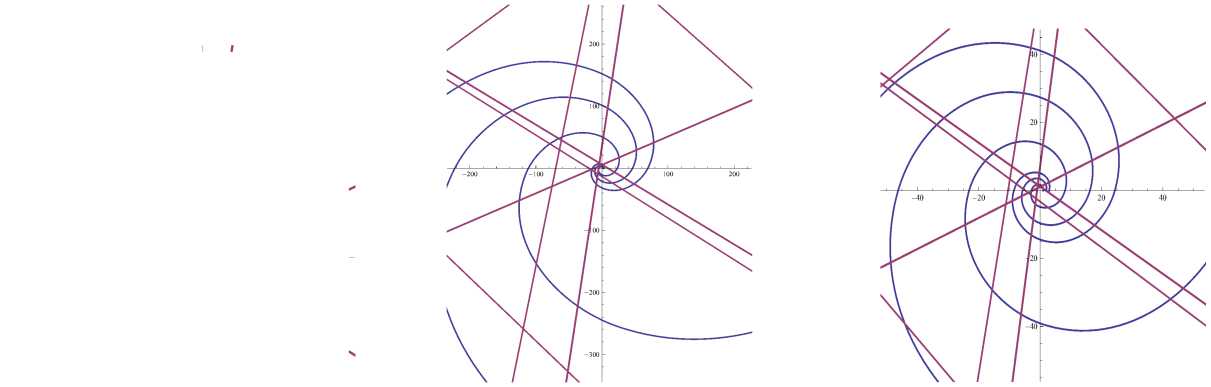
Рис. 11

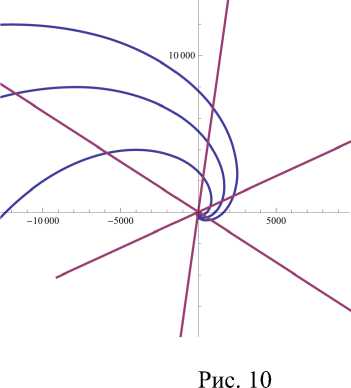
Рис. 12

Заметим, что при технологической реализации процесса изготовления армированной конструкции необходимо произвести вырез в виде некоторой окружности в начале координат, затем волокна располагают вдоль радиальных направлений. В качестве второго семейства армирующих волокон предлагается выбирать построенные изогональные траектории, т. е. найденные разнообразные семейства логарифмических спиралей.

Армирование по изогональным траекториям. Зададим некоторую криволинейную ортогональную систему координат ( ξ, η ) . Направим траектории армирования следующим образом: одна траектория армирования совпадает с линией криволинейной ортогональной системы координат, другая ей изогональна, т. е. пересекает ее под постоянным углом α, k = tgα . Тогда один угол армирования, например, ϕ ₁ = ^π₂ , второй угол армирования ϕ ₂ = arctg k . Другой вариант армирования – ϕ ₁ = 0 , ϕ ₂ = arctg k .

Запишем условие постоянства сечений волокон m -го семейства в соответствии с [4; 6]:

∂∂

( H ₂ ω _m cos ϕ _m ) + ( H ₁ ω _m sin ϕ _m ) = 0,     (16)

∂ξ              ∂η

ξ = ξ ⁰ = const ,    η = η ⁰ = const . Первое уравнение

в (17) можно проинтегрировать:

_{ω ( ξ,η ) =} H 2 ( ξ,η ⁰) ω 1 ⁰( ξ )

¹             H 2 ( ξ,η )

Поскольку криволинейная ортогональная система координат вводится аналитическими функциями комплексного переменного [6], то в каждой точке ( ξ, η ) коэффициенты Ламе равны между собой: H ₁( ξ,η ) = H ₂( ξ, η ) . При записи второго уравнения в (17) воспользуемся заменой ω ₃ = H ₁ ω ₂ = H ₂ ω ₂ , получим

∂(ω3)+k ∂(ω3)=0. (18) ∂ξ ∂η

Уравнение (18) является однородным дифференциальным уравнением с частными производными первого порядка, условия на интенсивности ω ₁ , ω ₂ на

контуре, где волокна входят в конструкцию, соответствуют задаче Коши. Ищем семейство решений, содержащих произвольную функцию, предварительно строим обыкновенное дифференциальное уравнение в форме

где H ₁ ( ξ, η ) , H ₂( ξ, η ) – дифференциальные коэффициенты Ламе; ω _m – интенсивности армирования, m = 1 , 2 . Для указанных структур армирования из

dξdη 1=k.

π

уравнения (16) в первом случае ( ϕ ₁ = ₂ , ϕ ₂ = arctg k )

получим

∂ (H1ω1sinϕ1)=0, ∂η

^∂ ( H ₂ ω ₂cos ϕ ₂) +^∂ ( H ₁ ω ₂sin ϕ ₂) = 0 .

∂ξ              ∂η

Дополнительные условия на интенсивности ω ₁ ,ω ₂ зададим на том контуре, где волокна входят в конструкцию. Предположим, что ω ₁⁰ ( η ) , ω ⁰₂ ( η ) , ω ₁⁰ ( ξ ) – известные функции, заданные на линиях

Находим общий интеграл (19), он равен - k ξ+ η = const . Тогда общее решение (18) запишем как

ω3=F1(-kξ+η),

где F1 – любая непрерывно дифференцируемая функция. Укажем очевидное решение: ω3 = const. Далее решаем задачу Коши. Пусть ω3=H2(ξ0,η)ω02(η) при ξ = ξ0. Разрешая общий интеграл (19) относительно переменной η , записываем искомое решение в виде

ω2 =

H 2 ( ξ ⁰ ,η ) ω ⁰ 2 ( - k ξ+η+ k ξ ⁰)

H 2 ( ξ,η )

Во втором случае ( Ф 1 = 0 , ф ₂ = arctg к ) уравнения (16) примут вид

“ 14 = H 1 ^E 2 ® 2 5_а

— ⁽ H 2 ^ю cos Ф , ) = 0 , 5^

“ 15 = ² H 2 ^E 2 ® 2 ⁵ а

k ³

(1 + к 2 ) 2 , k

(1 + к ²)2’

д

— ( Н ₂to₂ cos ф₂) +--( Я , to₂ sin ф₂) = 0 .

д_ ²² дп ¹²

Г         к2

“., = 2 H E ,ю₂---- —- + Q m. 1 2 ,

16        1 ( 2 2(1 + к2)24

Решения находим аналогично (17):

® 1 ( ^,П )

H 2 ( ^ ,п ) ю ° ( п )

H 2М

ю ₂

H Д^ ,п ) ю 2 ( - к ^ + 4 + к £ * )

H 2 ( ^,4 )

“- = H 2 E 2 ® 2 5 а (1 + ^к _{к 2})2 ,

Г                  к ² )

“- = H 1 I ^v m 3 ^{Q +} E 2 ® 2 (1 + _{к 2})2 I,

Полученные значения для интенсивностей армирования используем далее в работе для вычисления коэффициентов при построении разрешающей системы уравнений. Различные решения для интенсивностей приводят к различным разрешающим уравнениям задачи армированной среды.

В работе [6] установлена разрешающая система трех дифференциальных уравнений в криволинейных ортогональных координатах относительно трех компонент тензора деформаций е 11 , е ₂₂ , е ₁₂:

“ 23 = ^H 2 ^E 2 ® 2 ^_а

“ 24 = H 1 ( Q m 3 + E ₂ ю ₂

k 3

(1 + к2)2 ’ k4    )

(1 + к ²)²) ’

где

Г                     к ² )

“₂, = 2 H Q m , / 2 + E ₂to₂----- —- ,

^{25        2} ( ^{4         2 2} (1 + к²)² J

“₂₆ = 2 Я.Е₂ го₂5„ — ^к— , ^{26        1 2 2 а} (1 + к ²)²

Q = 1 - ( ю 1 + ю ₂); E , v - модуль Юнга и коэффи-

^д 2 ^е 22 , _г ^д2 ^е 11 , _г ^д2 ^е 12 , _г де11 ^де _п ,

+ С л + С э + Сд + С с + дс ²       дп д^дп дс дп

, _Г ^Е—, _Г ,^22, _Г^де 2 . _Г^де 2 , + C z     + С -7     + С о + С л +

⁶ д^ ⁷ дп 8 д^ 9 дп

^{+ С} 1° ^е 11 ^{+ С}11 ^Е 22 ^{+ С} 12 ^Е 12 = °;

де,,      де,,      де„      де„      де12

“" ,_; ⁺ “ '2       ⁺ “ '3       ⁺ “ '4 ' ⁺ “ '5      ⁺ '

д^     дп      д^      дп      д^

де12

“ v., ⁺ дп

+ F ( H 1 , H 2 , « 1 , « 2 , Ф 1 , Ф 2 , Ф 1 ,§ , Ф 1 ,п , Ф 2 ,^ Ф 2 ,п ) + H 1 H 2 Ф 1 = °;

де,,      де,,      де„      де„      де12      деп

“ 21 — ⁺ “ 22^" ⁺ “ 23— ⁺ “ 24™ ⁺ “ 25^1- ⁺ “ 26 — ⁺ д^     дп дс      дп      дс      дп

+ F 2 ( H 1 , H 2 , « 1 , « 2 , Ф 1 , Ф 2 , Ф 1 ,^ , Ф 1 ,п , Ф 2 ,^ Ф 2 ,п ) + H 1 H 2 Ф 2 = ° .

циент Пуассона материала связующего; Em – модуль Юнга материала m-го семейства армирующих воло-EE кон, m., =-----, m. =----. Значения символа 5„,

а

3 1 - v 4 1 + v входящего в выражения (21), равны единице или минус единице и учитывают выбор знака в формулах тригонометрии при переходе от синуса и косинуса угла а к его тангенсу в зависимости от величины угла армирования.

Исследуем тип разрешающей системы (20) для рассматриваемого случая армирования аналогично подходу [6]. Для этого найдем корни X характеристического уравнения

Значения коэффициентов Cs, s = 1, 12, через параметры Ламе приведены в [6]. В разрешающей системе (20) первое уравнение является уравнением совместности деформаций в произвольной криволинейной системе координат, два остальных уравнения – это уравнения равновесия плоской задачи в криволинейной системе координат, выраженные через компоненты деформаций е11, е22, е12. Для коэффициентов aij , в соответствии с введенным способом армирования, получаем выражения а,, = Я, (Qm + E, ю, + Е2 ю-

• ^{11       2       3      1 1      2 2}(1 + к ²)²

а„ = Я.Е2 го25„

• ^{12    122 а} (1 + к²)²

Г

“ 13 = H 2 I ^Qv m 3 ⁺ E 2 « 2 (1 ₊ k 2 ) 2

,

( “ 11 X 2 + “ 12 X )   ( “ ₁₃ X ² + “ 14 X )

( “ ₂₁ X ² + “ ₂₂ X )  ( “ ₂₃ X ² + “ ₂₄ X )

- 2 X

( “ 15 X ² + “ 16 X ) = ° , ( “ ₂₅ X ² + “ ₂₆ X )

где коэффициенты “ ij , i = 1 , 2 ; j = 1 , 6 из (21).

Уравнение (22) представляет собой полное алгебраическое уравнение четвертого порядка. Его коэффициенты зависят от технических характеристик материала связующего и арматуры, интенсивностей армирования волокнами первого и второго семейства и параметра k , который задается при построении траекторий, изогональных к данному семейству кривых.

Исследуем корни характеристического уравнения при фиксированном материале, но изменяя интенсивности армирования и параметр k. Рассмотрим следующие варианты комбинации выбора материала для матрицы (связующего) и арматуры (армирующих волокон): связующее – алюминий, армируем стальными волокнами; связующее – медь, армируем волокнами из вольфрама; связующее – графит, армируем волокнами из стали. Зададим различные варианты значений интенсивности и параметра k. Результаты представим в виде таблицы.

Получили, что все корни могут быть действительными; корни могут быть действительными и комплексно сопряженными; все корни могут быть комплексно сопряженными. Основное влияние на характер корней оказывает значение параметра k – тангенса угла армирования по изогональной траектории.

Как видим из таблицы, разные значения углов армирования приводят к разным типам системы разрешающих дифференциальных уравнений (гиперболическому, эллиптическому, смешанному типам), а следовательно, и к разным постановкам краевых задач. Им соответствуют существенно разные решения, что позволяет управлять напряженно-деформированным состоянием конструкции.

Многообразие структур армирования на базе ортогональной системы координат достигается путем построения изогональных траекторий к данным координатным линиям, оно зависит от выбора параметра k и значений интенсивностей армирования. С изменением структур армирования существенным образом изменяются поля напряжений и деформаций.

Таким образом, разработан метод получения многообразия новых структур армирования путем построения изогональных траекторий к некоторым заданным координатным линиям. Решения новых краевых задач неоднородной анизотропной теории упругости показывают широкие возможности управления полями напряжений и деформаций в плоских тонкостенных конструкциях за счет целевого выбора криволинейных структур армирования.