Моделирование деградационных процессов керамических изделий в эксплуатационных условиях

упомянуть керамику для медицины и других сфер человеческой жизнедеятельности.

Таким образом, изготовление керамических изделий (КИ), технология этого процесса имеют многовековую историю. Но динамика технологических усовершенствований не только не замедлилась, но в век информационных технологий приобрела ряд новых направлений.

Одно из этих направлений успешно использует возможности математического планирования, эксперимента (МПЭ) [1–3], что будет показано также на примере прогнозиро- вания долговечности образцов строительной керамики.

За время прикладного использования методов МПЭ для решения научных, инженерных и технологических задач накоплены значительный опыт и конкретные результаты [4–6 и др.] При этом движение прикладников шло как по традиционным путям, определенным принципами МПЭ, так и нетрадиционным, которые диктовали и вызывали потребности инженерной практики [7–9 и др.]

Для многих задач достаточно получить по результатам МПЭ регрессионную модель, связывающую некоторый параметр П объекта исследования (ОИ) с управляемыми воздействиями (факторами):

П ои = f ( x l , x 2 , x 3 ,-, x n ; b l , b 2 , ^b 3 ,-, b n ) =

= П ои ^f     A x 1 ,

V о x )

где х 1 , х ₂, ..., x n = { x i } - совокупность воздействий (факторов), каждый из которых влияет на исследуемый П ои ; b 1 , b 2 , b 3 , •••, b n = { b i } — параметры модели регрессионного анализа, коэффициенты влияния, отражающие вклад каждого x_i соответственно в П_ои.

Для решения ряда задач после получения зависимости П ои = | £— Д х | и выбора сово-

V д х ) купности факторов, обеспечивающих уровни П_ои, удовлетворяющие экспериментатора по его критериям, необходимо представить, например, некоторый прогноз поведения П_ои при длительной эксплуатации ОИ.

Пример решения такой задачи - прогнозирование срока службы керамических изделий, т.е. оценка временной продолжительности работы ОИ от начала эксплуатации до наступления отказовых явлений КИ (кирпича), широко используемого изделия, являющегося неизменным элементом при возведении зданий и сооружений.

Экспериментальное подтверждение долговечности КИ - серьезная проблема, поскольку для проверки в реальном масштабе времени (годы, десятилетия) такие исследования практически не реализуемы, а известные ускоренные методы [7-9] не дают достоверных результатов. Решение усложняет то обстоятельство, что износовые (деграда-ционные) явления зависят от воздействия на здания и сооружения климатических, механических и других факторов, что значительно расширяет спектр возможных специфических нюансов, которые необходимо учитывать при моделировании условий эксплуатации.

Был выбран путь, исходной базой которого явились результаты многофакторного планируемого эксперимента, проводимого на этапе отработки режимов изготовления и формирования технологического процесса изготовления КИ.

Обобщенно этот этап может быть представлен следующим образом. Первое - определение набора факторов, которые свелись к двум видам сырья х 1 , х ₂, температуре и продолжительности обжига х 3 , х ₄. Предполагалось наличие внутренних неуправляемых факторов (% добавок и влаги в подготовленном тесте). Указанные факторы определили матрицу планирования (МП), ориентированную на полученные на первом этапе линейные зависимости по всем факторам (МП – табл. 1).

Матрица планирования

Таблица 1

№ ОИ	х 1 / х 2	х 3	х 4	Результаты П ои
1	+	+	+	П 1
2	–	+	+	П
3	+	—	+	П 3
4	–	–	+	П 4
5	+	+	–	П 5
6	–	+	–	П 6
7	+	–	–	П 7
8	—	—	—	П 8

Факторы x_i варьировались на двух уровнях (минимальный – «–», максимальный – «+»; один из видов сырья был принят за нижний уровень – «–», другой – верхний – «+»).

МП явилась исходной информационной базой для подготовки технологического процесса, определения технологического оборудования, режимов и условий испытаний при реализации МПЭ. Результаты МПЭ отражались в последнем столбце МП (Пои – предел прочности КИ на сжатие).

На рис. 1 представлены факторограммы, которые иллюстрируют результаты опытов: по оси абсцисс отложены номера опытов N_i согласно МП, по оси ординат - значения П_ои, полученные в соответствующих опытах.

Результаты отмечены на соответствующих осях точками, которые для наглядности

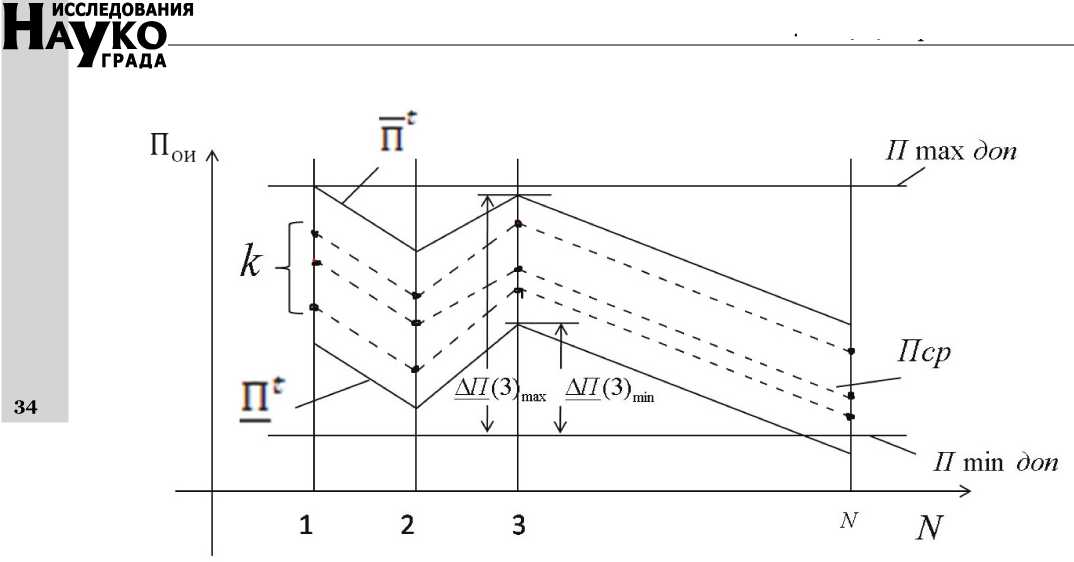
Рис. 1. Совокупность факторограмм (коридор откликов)

соединены прямыми. Ломаные кривые, соответствующие одной серии опытов, - факторо-граммы; совокупность К факторограмм образует коридор откликов.

Одну факторограмму дают испытания образцов КИ из одного сырья с одинаковыми процентами влаги и добавок, а изменение сырья и случайные изменения внутренних факторов смещают факторограммы (К факторо-грамм), однако все факторограммы в пределах коридора откликов демонстрируют общую для всех результатов тенденцию (изменение Пои при переходе от опыта к опыту).

Такой подход - отступление от «классического» МПЭ, оперирующего с одним ОИ, что связано с необходимостью формирования стратегии изготовления массовой продукции, какой являются КИ.

Учитывая ограниченное количество исследуемых образцов (малая выборка), которые не могут отразить тенденции при массовом изготовлении, необходимо оценить возможные границы разбросов П_ои при массовом производстве КИ, например, толерантные пределы П t_N возможных результатов в каждом опыте [10]:

П N = П ср ± kS ( N ), tt где П N - толерантные пределы ( П N - нижний, П ^t _N – верхний), в каждом опыте (1, 2, 3, …, N ) – рис. 1;

Пср – среднее значение Пои в каждом опыте;

k t - толерантный коэффициент (табулированный [10]);

S ( N) - оценка среднеквадратичного отклонения П_ои в каждом опыте:

2 ? (П n - П ср )² к - 1        ^,

5 ( N ) =

где k – количество испытанных образцов.

Если на полученные результаты нанести допустимые пределы (рис. 1) для исследуемого П_ои (в нашем случае предел прочности на сжатие), то разн _t ость между толерантными пределами П ^t , П и нижним ограничителем П_minдоп определяет запасы работоспособности ΔП КИ по отношению к указанному пределу (ограничению) в каждом опыте:

Д E = П t — П _min доп - по отношению к нижнему ограничению, _t

– по отношению к max доп верхнему ограничению (рис. 1)

При исследовании долговечности КИ, естественно, определяющими являются первые запасы ∆ П .

Полученные результаты, в частности, могут быть использованы при выборе того технологического процесса изготовления КИ (в зависимости от спроса, наличных ресурсов и т.д.), который, обеспечивая необходимый Пои, одновременно обладал бы необходимым запасом работоспособности. Так, если выбраны режимы и условия изготовления КИ, определенные, например, опытом 3 (температура и продолжительность обжига, сырье, процент примесей), то при этом будет обеспечен минимальный запас работоспособности AH(3)min (рис. 1). Естественно, если в оценочный процесс ввести вероятностные показатели, то запасы работоспособности могут отсчитываться от среднего значения Пои в каждом опыте. В принципы моделирования износовых процессов это не вносит принципиальных изменений.

Так как оценен минимальный запас работоспособности -A H(3)_min - и известно время, в течение которого изготовитель гарантирует сохранение П_ои не ниже П_minдоп(t_г), возможно получить минимально допустимую скорость V _min расходования указанного запаса:

V ■ min

-Д П(зи t _г

Введение понятия запаса работоспособности позволяет количественно оценить на- личие превышения прочности на сжатие относительно минимально допустимого уровня. Если такого запаса нет, то образцы КИ соответствующей марки, обладающие прочностью на нижней границе коридора откликов (рис. 1), могут разрушаться уже в процессе строительства.

Образцы, обладающие запасами работоспособности, снижают (расходуют) их из-за развития внутренних дефектов, прогрессирующих во времени.

Физическое моделирование расхода запасов зависит от физической модели развития дефектов, определяющей технологию моделирования влияния реальных эксплуатационных условий.

Была принята следующая физическая модель развития внутренних дефектов. Одна из преобладающих причин – пористость КИ. Увеличение размеров пор, возникновение микротрещин, объединяющих мелкие поры в полости (пустоты) значительных размеров, – все это снижает прочность КИ.

Пористость КИ обуславливает влаго-поглощение последних. Влага, заполняющая поры, при снижении температуры до уровня замерзания воды расширяется и приводит к возникновению внутренних усилий, вызывающих образование микротрещин, соединяющих и объединяющих соседние поры. После повышения температуры и размораживания воды в порах увеличенный объем не может быть заполнен прежним количеством влаги, что приводит к снижению давления и привлечению в новые объемы пор дополнительной влаги. Указанные процессы обладают цикличностью в период весенне-осенних переходных периодов, когда температурные условия нестабильные и знакопеременные (ночные заморозки сменяются дневной положительной температурой). При этом количество циклов различно для каждого региона обширной Российской Федерации. Летние и зимние условия с учетом выбранной модели являются константными и практически не вносят вклад в развитие внутренних дефектов. Кроме того, развитию внутренних дефектов и снижению прочности КИ способствуют сопутствующие механические воздействия, возникающие от близости железных дорог, строек (забивание свай) и других производственных условий.

С учетом принятой физической модели развития и накопления внутренних дефектов ускорение выявления расходования потенциальных прочностных запасов при моделировании условий эксплуатации возможно за счет создания температурного циклирования с одновременным механическим воздействием и исключения временных промежутков между циклированием, обладающих относительно стабильными температурными режимами (зима, лето), а также сведения до технологического минимума длительности переходных температурных режимов (повышение, понижение), которые в реальных условиях достигают 6–8 часов.

Оценка годовых эквивалентных температурных циклов при эксплуатации была принята равной 25-30. После 250-300 циклов с последующим действием вибрациями (совместить термоциклы и вибрацию не позволило оборудование) из партии испытываемых КИ извлекались образцы, на которых проверялось снижение прочности Пои за счет износов процессов. С оставшимися КИ продолжали моделирующие процедуры (циклы), каждый раз определяя уменьшение запасов работоспособности и оценивая скорость расходования последних.

Так как все повторные циклы эквивалентны годовым (предположительно) срокам реальной эксплуатации, полученные результаты позволяют:

• -    оценить и уточнить (при необходимости) принятую модель равномерного расходования запасов;

  
  

ИССЛЕДОВАНИЯ