Моделирование дифракции света на полуплоскости методами геометрической оптики

Дифракция на полуплоскости является одной из классических задач, для решения которых создавалась волновая теория света [1]. С 40-х годов XX века много научных работ было посвящено разработке различных математических моделей дифракции микроволнового излучения на полуплоскости [2, 3]. Эти модели активно используются при расчетах распространения коротковолнового излучения на пересеченной местности и в городской застройке [4]. Моделирование дифракции на полуплоскости имеет важное значение в акустических расчетах [5, 6].

При расчетах оптических систем моделированию дифракционных явлений на отверстиях различной формы традиционно уделяется значительно больше внимания, чем моделированию дифракционных явлений на краю полуплоскости. А в компьютерной графике и в фотометрических расчетах дифракционные явления часто не учитывают. Если дифракционными явлениями можно пренебречь, то для моделирования распространения оптического излучения становится возможным использовать пучки лучей [7, 8, 9]. В этом случае луч интерпретируется как геометрическая линия. На каждый луч из рассматриваемого пучка нанизана (терминология из [7]) определенная доля потока излучения. При данном способе моделирования поток излучения, который падает на заданный участок поверхности, почти всегда принимается равным алгебраической сумме потоков излучений, нанизанных на те лучи, траектории которых пересекают этот участок поверхности. Алгоритмы расчета траекторий лучей очень хорошо отработаны. Так как траектория каждого луча может быть вычислена независимо от траекторий других лучей, то это позволяет распределять вычисления по нескольким процессорам.

Было предложено несколько способов дополнить описанную модель распространения оптического излучения так, чтобы она стала пригодной для расчета дифракционных явлений, но при этом было сохранено условие алгебраического сложения нанизанных на лучи потоков излучений.

В работах [10, 11, 12] предложено для моделирования дифракционных явлений с сохранением условия алгебраического сложения нанизанных на лучи потоков излучений воспользоваться квантовой теорией света совместно с принципом неопределенности Гейзенберга. При моделировании этим методом принимается, что при прохождении через отверстие направление луча изменяется по случайному закону. Чаще всего для описания распределения вероятности отклонения луча выбирается закон Гаусса. В этом случае моделирование дает достаточно гладкое распределение энергии в дифракционной картине, без ярко выраженных и весьма характерных максимумов и минимумов.

Другой вариант моделирования дифракционных явлений с сохранением условия алгебраического сложения нанизанных на лучи потоков излучений основан на использовании преобразования Вигнера [13, 14, 15, 16].

В статье [17] продемонстрирована возможность моделировать пространственное распределение потока излучения в многомодовом Эрмито– Гауссовом пучке с помощью набора лучей с нанизанными на эти лучи потоками излучений с сохранением условия алгебраического сложения этих потоков. Нанизанный на луч поток излучения в этом случае прямо пропорционален удельной tan-силе света [18] источника излучения. Данная удельная tan-сила света зависит как от линейных координат точки пересечения луча с плоскостью источника излучения, так и от направления луча в этой точке. Для математического описания удельной tan-силы света источника излучения используются полиномы Эрмита (см. приложение 1) и функция Гаусса. Основная проблема использования результатов работы [17] для численного моделирования дифракции на полуплоскости связана с тем, что возникающую в результате дифракции волну необходимо представить в виде многомодового Эрмито-Гауссового пучка. Однако из рассмотренного в приложении 2 примера следует, что такое представление едва ли целесообразно.

В настоящей работе описанный в статье [17] метод математического моделирования будет модифицирован так, чтобы с его помощью можно было моделировать дифракцию на полуплоскости.

1. Математическое описание дифракции на полуплоскости

По аналогии с работами [13, 14, 15, 16, 17] при описании электромагнитного излучения будем использовать скалярное приближение.

Пусть непрозрачный экран в плоскости OXY полностью перекрывает полуплоскость x <0. Этот экран ограничивает плоскую волну, нормаль к волновому фронту которой совпадает с ортом оси OZ , а амплитуда равна W ₀. Тогда в плоскости OXY комплексная амплитуда волны описывается выражением

W ( x , y , z = 0) = W o % v ( x ), (1)

где % v (x) - функция Хевисайда (1).

При z > 0 комплексная амплитуда волны W ( x , y , z ) удовлетворяет параболическому волновому уравнению [19]

Э2W Э2W 4m ЭW

--1------

Эx2   Эу2    X Эz где X - длина волны излчения, i = V-1.

В точке с координатами x, у, z интенсивность дифрагировавшей волны равна [1 ]:

J ( x , у , z ) = 2 W ( x , У , z ) W * ( x , У , z ),

где индексом * обозначены комплексно сопряженные величины.

На основе преобразования Вигнера [20] интенсивность дифрагировавшей волны можно представить в виде

w02 Г Г

J ^{( x} , у , ^z ) = — J J % ^{v (} u + ^v ) % ^{v ( v -} u ) ^х

-M -M

4л z , х cos —u (x - v) dudv. Xz

После подстановки формулы (1.4) в выражение (4) получим

+ m

к        V W 0²      м Г '-> ^ю2^л2

J ^{( x} , у , ^z )= ^— I P m ^{( v )e}xp -2—— m =0 z X -M                X ² z ²

-M

2 m

2 юл      a j

⁽ x - v ) d v , X z

( x - v ) ² х

^J (5)

где Hl (•) - полином Эрмита (см. приложение 1), ю - параметр,

P_m ( v)

4 ^m (2 m )!

( 2 u ² L

X exp--- H 2 m

I ю ² )

+ m

J % v ( u + v ) % v ( v - u ) X

-M

( 2 u

— d u .

I ю J

В приложении 3 показано, что формулу (5) можно преобразовать к виду

1 ~ ( - 1) m

J ^{( x} , у , ^z ) = 8 ^{( x} )⁺ - £ Y-^X z m-0 4 m m !

+ m

J T ( m + 1, m , v ) L

-M

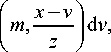
где k!     ( 2v2V  (2v

T ⁽ P 1 , p 2 , ^v )= % ^{v ( v} ) £ —exp-- 7 ^H 2 k - 1 — ,(8) k = P 1 (2 k )!     ( ю² )      (^ ю J

\       2^2     ( , ю ² л ² Y     ( 2 юл ^

L ⁽ q , ^v ) = ^W o² ю—— exp l - 2—— ^{v 2} I H 2 q I —— ^v I ,⁽⁹⁾ X ^    X ²     J у X J

W 0²    (Д x ^       W 024 2

8 ( x ) = —erf ---- % v ( x )-- ^T (1, m , x ). (10)

2   ^ ю J Vn

В работе [17] доказано, что если в плоскости z = 0 расположен источник излучения, то освещенность в плоскости z = L >0 равна

+m +m

— J J G I u , v YY, Y -Y I d u d v ,           (11)

z2 J J I L L J -M -M где G(u,v,u,v) - удельная tan-сила света в точке с координатами x = u, у = v, z = 0 в направлении вектора, чьи координаты равны x = ui, у = v , z =1. Если удельная tan-сила света в плоскости z = 0 описывается выражением

G ( x , у , x у ) = AT ( P 1 , p 2 , x ) L ( q , x ) 8 ( у ) 8 ( у ),      (12)

где 8 ( ^ ) - дельта-функция Дирака, A - произвольная константа, то освещенность в плоскости z = C равна

+ м +м

J J T ⁽ P 1 , P 2 , v ) L -M -M

Л +м               ( q, x—v 8(u)8 у—u dudv =

^{L J 1 L J} (13)

= — J Т ( P 1 ,P 2 , v ) L I q Дт^ I d v .

z                     L

-M

На основании формул (7), (13) интенсивность излучения в плоскости z = L может быть представлена в виде суммы

■XI

J ( x , y , z = 0 = 8 ( x ) + £ E m ( x , &              (14)

m =0

где E m ( x, ^ ) - освещенность в плоскости z = ^ от расположенного в плоскости z = 0 источника с удельной tan-силой света

( - 1) m

—— T ⁽ т ⁺ 1,^х, x)^L (q , x ) 8 ⁽ y ) 8 ⁽ у ).

4 ^m m !

Функцию E ( x ) можно рассматривать как освещенность в плоскости z = £ от расположенного в плоскости z = 0 источника с удельной tan-силой света

^{8 ( x} ) § ⁽ У ) § ⁽ У ) § ^{( x )}.

Из формулы (14) следует, что от набора источников, удельная tan-сила света которых описывается выражениями (15) и (16), формируется такое же распределение излучения в пространстве, как и при дифракции плоской волны на полуплоскости. Для математического моделирования исходящего излучения от источника с известной удельной tan-силой света (следовательно, и для математического моделирования дифракции на полуплоскости) можно использовать хорошо известные в вычислительной оптике и компьютерной графике методы на основе расчета лучей с нанизанными на эти лучи потоками излучения. В этих методах поток излучения, который падает на заданный участок поверхности, принимается равным алгебраической сумме потоков излучений, нанизанных на те лучи, траектории которых пересекают этот участок поверхности.

Необходимо отметить, что функция (15) при некоторых наборах величин x , x может принимать отрицательные значения. Этот факт обсуждался в работах [14, 16].

2. Численное моделирование

В качестве примера будет рассмотрен простейший случай, когда сформированный в результате дифракции поток излучения проходит через однородную, не рассеивающую и не поглощающую среду и падает на плоскость z = ^ . Такой выбор обусловлен тем, что в данном случае результаты расчета можно сравнить с аналитическим решением [1]. Действительно, легко проверить, что функция

^W0- Г S f ^2    1 + - +2i ,   ^z^ J 2

W ( x , y , z )

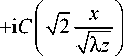
1 i

где

^S ®=Г sin ^f^{d u} ,    C ®⁼Г cos ^r^{d u}

интегралы Френеля [21, 22], является решением параболического уравнения (2) при начальных условиях (1). В точке с координатами ( x , y , z ) интенсивность дифрагировавшей волны (17) равна:

2 W ( x , у , z ) W * ( x , у , z ) = 24- x

+ —

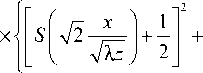
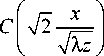
Разделим полуплоскость z = 0, x >0 на (2My + 1)×(Mx + 1) прямоугольных ячеек. Стороны данных ячеек параллельны осям OX и OY соответственно, а центры расположены в точках xix= Ax (ix +1/2);     у, = Ду (iy +1/2), xy где    Дx,    Ду   - длины сторон    ячеек, iу =0, ±1, ±2, ±3,..., Му, ix = 0, 1, 2, 3,., Mx.

Для математического моделирования используем набор базовых лучей [моделируют распределение освещенности от источника с удельной tan-силой света (16)] и набор боковых лучей [моделируют распределение освещенности от источников с удельной tan-силой света (15)]. Базовые лучи проходят через центры всех ячеек и перпендикулярны плоскости z = 0 . На базовый луч, который проходит через точку ( x i _x , y i _y ), нанизан поток излучения

ДФ гау = Д x Ду X

V Wo2  г x — erf

ix

и

% v ⁽ x,_x)--г

x

л

T (1, K , x x ) ,

где в соответствии с выражением (10) K должно быть бесконечно большим. Однако в численных расчетах в качестве значения K должно быть принято достаточно большое, но конечное число.

Траектории боковых лучей описывают уравнения

у = у,- ; x = x + x, z, iyixj где

x j = Д tan ( j + 1/2),

Д _tan - параметр математической модели, j =0, ± 1, ± 2, ± 3,..., M_x . На боковой луч, который описывается уравнениями (20), нанизан поток излучения

к ( - 1) m

ДФ гау = Д x Д у Д tan £     ' /T ( т + 1, K , x ) L ( т , x j ) . (22)

m =0 4 ^m m !               ^x

Разделим плоскость z = ^ на сеть из прямоугольных ячеек. Стороны данных ячеек параллельны осям OX и OY соответственно, а центры расположены в точках

^ lx = Д₅ ( l x + 1/2); п _1у = Д п ( Уу + 1/2),

где Д ^ , Д^ - длины сторон ячеек, l y = 0, ± 1, ± 2, ± 3,..., l y = 0, ± 1, ± 2, ± 3,... Поток излучения Ф cel , который падает на ячейку в плоскости z = £ , равен

Ф c_ell = ^ ДФ ray ,

где суммирование ведется по всем центральным и всем боковым лучам, которые попадают в данную ячейку. Средняя освещенность в этой ячейке равна

Ф и cell

.

Д^ДП

Средние значения освещенности в ячейках, соотнесенные с центрами ячеек, аппроксимируют значения освещенности в плоскости z = ^ .

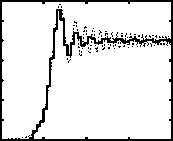
На рис. 1, 2, 3, 4 представлены результаты расчетов при X = 0,5 мкм, Д x = Д _y = 4^10 ³ мм, Д _tan = 2,5^10 ^-5, Д ^ = Д_л = 4^10 ^-2 мм, M x =5000, M y = 5000, M x = 5000, Ю = 0,5 мм. Эти графики показывают, что результаты расчетов методом геометрической оптики хорошо аппроксимируют аналитическое решение [формула (18)] при x < 0. При x >0 аппроксимацию можно считать удовлетворительной на интервале, в котором лежат несколько первых максимумов и минимумов функции (18). Длина этого интервала увеличивается с увеличением числа K . За пределами указанного интервала расчет методом геометрической оптики дает сглаженные значения функции (18).

0,7W_q² 0,6W°²

O,5Wo2

J O,4Wo2 O,3Wo2 O,2Wo2 O,1W 2 0

• -0,5    0    0,5    1    1,5

x,mm

Рис. 1. Освещенность в плоскости z = 100 мм: сплошная линия – результаты моделирования методом геометрической оптики (K = 25); пунктирная линия – результаты расчета по формуле (18)

O,7Wo2

O,6Wo2

O,5Wo2

J O,4Wo2

O,3Wo2

O,2Wo2

O,1W 2 0 0

• -0,5    0    0,5    1    1,5

x,mm

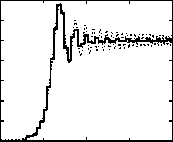
Рис. 2. Освещенность в плоскости z = 100 мм: сплошная линия – результаты моделирования методом геометрической оптики (K = 50); пунктирная линия – результаты расчета по формуле (18)

Заключение

Предложенный в статье способ моделирования дифракции на полуплоскости можно использовать в тех случаях, когда дифракционные эффекты не являются определяющими, однако учесть влияние дифракционных явлений все же желательно. Указанные обстоятельства типичны для задач трехмерной компьютерной графики, фотометрии, светотехники и часто имеют место при моделировании работы оптикоэлектронных систем. Если полностью пренебречь дифракционными явлениями, то весьма удобным и хорошо отработанным методом решения этих задач является построение траекторий лучей с последующим суммированием потоков излучения, которые нанизаны на эти лучи. Это связано с тем, что лучами с нанизанными на них потоками излучения хорошо моделируется отражение излучения от гладких и шероховатых поверхностей, рассеяние и поглощение света в средах, преломление на границе сред и т. д. Важнейшим достоинством предложенного в данной статье метода моделирования дифракции является сохранение условия алгебраического сложения нанизанных на отдельные лучи потоков излучения. Поэтому предложенный метод сравнительно легко можно использовать для модернизации существующих методов решения задач трехмерной компьютерной графики, фотометрии, светотехники и моделирования работы оптико-электронных систем. Так как в большинстве этих задач дифракционные явления не являются определяющими, то достаточно учитывать первые два или три порядка дифракции. А именно это и обеспечивает предложенный в статье метод.

O,7Wo2

O,6Wo2

O,5Wo2

J 0,4W02

O,3Wo2

O,2Wo2

O,1W 2 0

-10 12 3 4

x,mm

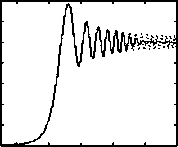
Рис. 3. Освещенность в плоскости z = 1000 мм: сплошная линия – результаты моделирования методом геометрической оптики (K = 25); пунктирная линия – результаты расчета по формуле (18)

0,7W02 0,6WQ2

O,5Wo2

J O,4Wo2

O,3Wo2

O,2Wo2 o,iwo2 0

-10 12 3 4

x,mm

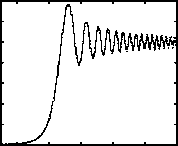
Рис. 4. Освещенность в плоскости z = 1000 мм: сплошная линия – результаты моделирования методом геометрической оптики (K = 50); пунктирная линия – результаты расчета по формуле (18)

Можно указать на несколько направлений повышения эффективности предложенного метода. Первое направление предполагает использование прямоугольных ячеек в полуплоскости (z =0, x >0), размеры которых оптимально выбираются в зависмости от расстояния от центра ячейки до края плоскоскости. Аналогично, параметры xj могут рассчитываться не по формуле (21), а более оптимальным с точки зрения эффективности образом. Еще одним направлением повышения эффективности может быть использование псевдослучайных чисел (методы Монте–Карло).