Моделирование динамических характеристик стабилизированного составного импульсного преобразователя

Составные импульсные преобразователи [1, 2] до настоящего времени слабо изучены, что препятствует обоснованному применению их на практике. Однако применение составных преобразователей целесообразно, например, в активных корректорах коэффициента мощности [3], в импульсных регуляторах-модуляторах ключевых генераторов модулированных колебаний (КГМК), поскольку позволяет обеспечить электромагнитную совместимость с цепью питания и последующим генераторным каскадом [3, 8]. Важным недостатком базового инвертирующего импульсного регулятора с таким же диапазоном регулирования выходного напряжения является импульсный характер передачи энергии, что заставляет использовать дополнительные фильтры на входе и выходе преобразователя [2, 3].

Динамические характеристики КГМК наряду с характеристиками в квазиустановившемся режиме определяются, в основном, динамическими параметрами регулятора-модулятора. В то же время при построении его системы управления должна учитываться особенность топологии составного импульсного конвертера с магнитносвязанными дросселями для обеспечения совместимости апериодического и колебательного процессов в КГМК.

амплитудно-частотная характеристика (АЧХ) является важнейшей, так как по ней определяется верхняя граница рабочего диапазона частот линейной системы, чувствительность замкнутой системы к изменению входного напряжения а также ее устойчивость при замыкании обратных связей, например, с использованием частотных критериев Найквиста [9].

Как известно, АЧХ линейной системы сравнительно просто можно получить из ее передаточной функции (ПФ), которая для непрерывной линейной модели (НЛМ) разомкнутой системы управления преобразователем получена в работе [10] в виде передаточных матричных функций (ПМФ) его составных частей. Передаточная функция НЛМ удобна не только для определения динамических показателей, но и для моделирования систем, представленных структурными схемами [5, 9], по сравнению с импульсными моделями [6], главный недостаток которых – большая сложность получения частотных характеристик.

Цель данной статьи – моделирование динамических свойств стабилизированного составного импульсного преобразователя с магнитно-связанными дросселями на основе передаточных функций.

Рассмотрим процесс и результаты моделирования с использованием ПМФ стабилизированного составного импульсного преобразователя с магнитно-связанными дросселями, работающего в режиме непрерывной проводимости силового коммутатора [4]. Общая схема системы управления (рис. 1) состоит из двух контуров регулирования – внешний по среднему значению входного напряжения второй части составного конвертера и внутренний по суммарному току магнитно-связанных дросселей.

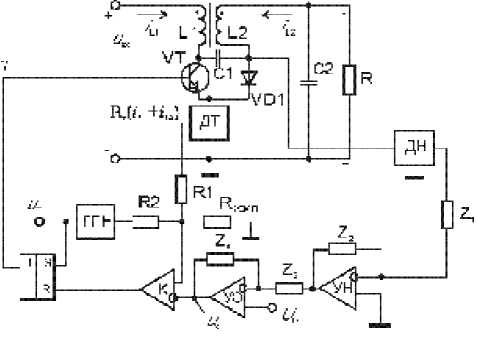
Рис. 1. Общая схема управления по среднему значению входного напряжения второй части конвертера и максимальному току ключа

Она содержит: датчик напряжения ДН с согласующим усилителем УН, усилитель ошибки УО, компаратор К, датчик тока ДТ и генератор пилообразного напряжения ГПН, RS-триггер. Диаграммы сигналов на элементах схемы представлены на рис. 2.

При частоте изменения входных сигналов много меньше частоты коммутации f к — 1 / Т , согласно рис. 2, может быть составлено уравнение для момента окончания импульса, в котором сигнал управления Y рассматривается как непрерывная переменная [5]:

R T ^{( i}кл + ^KY ^/2 f к ) + m nY / f к = ^U _E - ⁽¹⁾ где U _E - выходное напряжение усилителя ошибки; R _T – сопротивление токового датчика; 1кл = ^L 1 ср + ^L 2 ср — ток силового ключа (транзистор VT) в середине импульса (рис. 2); к , т _П -тангенсы угла наклона тока силового ключа и пилообразного сигнала соответственно; m П = U M / T ; U M — максимальное значение пилообразного напряжения.

Для исследуемого регулятора при сбалансированном снижении уровня пульсаций токов на интервале импульса коэффициент k равен [4, 8]:

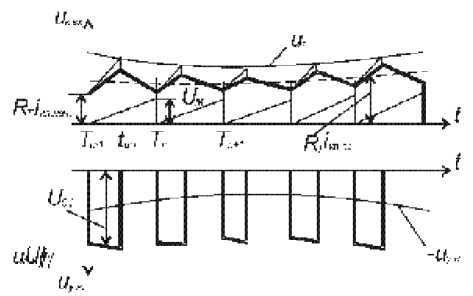
Рис. 2. Диаграммы сигналов на входах компаратора, датчике напряжения и усилителе напряжения при управлении по среднему значению напряжения и максимальному току di In кл             вх к —     —           , dt    (1 + kC ) L 2

где (1+k _c )L ₂ – эффективная индуктивность вторичной обмотки интегрированного дросселя; k _c – коэффициент магнитной связи.

Уравнение управления (1) относительно уп- равляющего сигнала у после линеаризации его в окрестности периодического режима ивх — Uвх и Y — Г, приводится к следующему уравнению в общей матричной операторной форме, при нулевых начальных условиях:

~⁽ Р ) ^— F ⁽ Р )~ ⁽ Р ) + Q ⁽ Р ) ~⁽ Р X ⁽²⁾ где F(р), Q(р) – матрицы-строки, связывающие коэффициент g с вектором переменных состояния и вектором входных воздействий, соответственно записываются в виде

F _{( Р} ) _{— -} (1 + ^k C ) ^L 2 f K d n 1 ^K ( Р ) K u ( Р ) Г 1 0

U bx      L         R t             ’

Q ( р ) —-    Г^ П     [ 1        0      0 0j

U вх

В соотношениях (3) К _и ( р ) - коэффициент передачи усилителя напряжения УН с учетом элементов ДН (передаточная функция ПФ датчика напряжения); K (р) – коэффициент передачи УО с учетом цепей коррекции;

U вх

П               (1 + k _c) L₂ "

U вх + m П---

R _T

Получение математической модели регулятора в форме пространства состояний по дифференциальным уравнениям силовой части преобразователя [10] вызывает серьезные затруднения. Для решения этой задачи, используя метод разделения движений [7], сводим исследуемую систему к двум системам второго порядка, описывающих первую и вторую части составного преобразователя соответственно.

Используя этот принцип построения, получена непрерывная линейная модель НЛМ составного преобразователя с магнитно-связанными дросселями и двухконтурной системой управления в виде структурной схемы (рис. 3) на основе передаточных матричных функций (ПМФ) разомкнутых контуров управления его составных частей [10]. Причем каждая ПМФ содержит НЛМ соответствующей силовой части и управляющую часть.

Здесь передаточные функции W ₂ (p), W ₃ (p) и W ₄ (р) передают сигналы, формирующие управляющий сигнал ~( р ) ; W i 1 _Y ( p ) и W i _{2 Y} ( p ) -передаточные функции “ток дросселя первой

3,fw

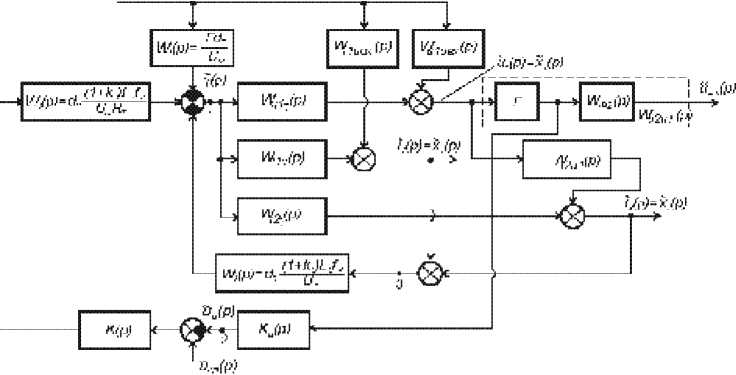
Рис. 3. Стру ктурная схема замкнутого составного преобразователя с магнитно-связанными дросселями

части – управляющий сигнал” и “ток дросселя второй части – управляющий сигнал” соответственно; W u _{1 Y} ( P ) - ПФ “напряжение на конденсаторе первой части – управляющий сигнал”; W _u 2 u i ( Р ) — ПФ “Напряжение на выходном конденсаторе - входной сигнал”; W i _{2 u} 1 ( Р ) -ПФ “Ток дросселя второй части – входной сигнал”; W _{i1 uвх} (p) – ПФ “ток дросселя первой части – входное напряжение”; W _{u1 uвх} (p) – ПФ “Напряжение на конденсаторе первой части – входное напряжение”.

ОЦЕНКА УСТОЙЧИВОСТИ НЛМ ПРЕОБРАЗОВАТЕЛЯ С УЧЕТОМ ПФ РАЗОМКНУТОЙ СИСТЕМЫ

Размыкание схемы в точке 2 (рис. 3) при структурном преобразовании внешней цепи главной обратной связи и сигнале и_хх ( р ) = 0 позволяет получить ПФ разомкнутой системы:

Wpa32(Р) = K(Р)Ku (РЖ(Р) х х      Wu 1у (РWu2и 1(Р)

^Х 1 + W 2 ( Р ) [ W 1 у ( Р ) + W 2 у ( Р ) ] ’ где передаточные функции

Wu 1 М =

и.f1-Р ™ ]

^вх (     ( Г )² д_э )

р 2 (1 + k c ) L 1 C 1 + Р + ( Г / ⁽⁶⁾ R _Э

W u 2 u 1 ( Р )

Г р2 (1 + kc )L2C2 + р ”   рC^ 2 + 1 (7)

R

Известно, что при динамическом синтезе систем управления импульсными преобразователями предпочтение отдается частотным методам, что обусловлено их наглядностью и возможностью сравнительно легко исследовать устойчивость систем высокого порядка. Применяя метод имитационного моделирования с использованием программных пакетов Matlab и MathCad и структурных преобразований исследуемой НЛМ регулятора-модулятора, получены частотные характеристики вариантов ПФ разомкнутых контуров НЛМ при и _хх (р) = 0.

Анализ устойчивости по логарифмическим частотным характеристикам проводился при следующих исходных данных:

2 U^ [ р RC + 1 ] Д э Н  ² J

W ^{( Р} )

Р ²(1 + k c ) LC + Р ' L + ( г )²

R _Э

K. ( Р ) = -K 4; К ( Р ) = К,

PT 1 ^{+ 1}

PT 2 ^{+ 1}

"7 Г Г'⁽⁸⁾

W 2 у (Р ) =

Ur ( рДС2 +1)

^{Р 2(1} + k c ) L 2 ^C 2 ⁺ р”  R ^{C 2 + 1}

где К ₁ – коэффициент передачи звена ДН по постоянному току; Т ₁ – постоянная времени ДН; К ₂ – коэффициент передачи усилителя ошибки; Т ₂ и Т ₃ – постоянные времени форсирующей и интегрирующей составляющих дополнительного звена УО.

U _вх = 27 В; U _С1 = 40 В; I _Н = 1 А; f = 120 кГц; L ₁ = 274 мкГн; L ₂ = 278 мкГн; k _С = 0,86; C ₁ = 6,6 мкФ; C ₂ = 6,6 мкФ; K ₁ = 0,38; K ₂ = 1,1; U _М = 1 В;

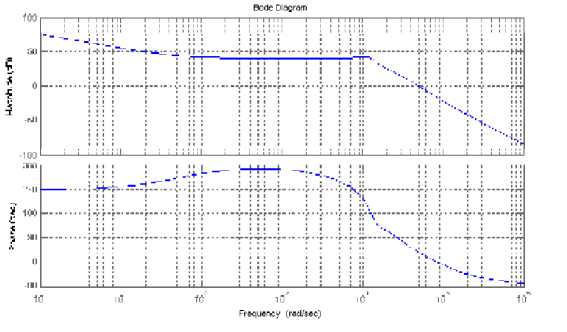
Рис. 4. Частотные характеристики разомкнутой в точке 2 системы при управлении по выходному напряжению и суммарному току

T ₁ = 0,9 ^. 10^-4с; Т ₂ = 0,02 с; Т ₃ = 0,001 с; R_T = 0,1 Ом.

Эффективность подключения токового контура можно увидеть из частотных характеристик, построенных по вышеприведенным исходным данным и показанных на рис. 4.

Общим для частотных характеристик, представленных на рис. 4 является то, что система обладает необходимым запасом устойчивости (демпфирование с внесением положительного фазового сдвига), система является гарантированно устойчивой, несмотря на наличие “правого” нуля в ПМФ первой части НЛМ.

ОПРЕДЕЛЕНИЕ ЧУВСТВИТЕЛЬНОСТИ ВЫХОДНОГО НАПРЯЖЕНИЯ

ЗАМКНУТОГО ПРЕОБРАЗОВАТЕЛЯ КО ВХОДНОМУ

В работе [10] приведены алгоритмы получения передаточных функций составных частей стабилизированного импульсного преобразователя. Располагая ПФ замкнутой системы, можно выяснить, каким образом выход преобразователя реагирует на изменение выходного напряжения, а также анализировать получаемые переходные процессы. Требуемые ПФ находим из передаточных матричных функций системы, причем ПМФ “переменные состояния – входные сигналы” достаточно просто можно получить [5, 10] из НЛМ силовых схем и уравнений управления составных частей исследуемого преобразователя.

Отсюда ПМФ замкнутой системы управления для первой части преобразователя описывается следующим уравнением:

H„AP ) = [ pE - A , - HF , ( P )№ + HQ , ( P ) ] (9)

Соответственно – для второй части преобразователя ПМФ описывается соотношением H , ( P ) =[ pE - A , — HF ( P )№ , + HQ ( P ) ] (10) при этом общая ПМФ замкнутой системы управ-

ления преобразователя представляет собой произведение ПМФ составных частей

^Hxu ⁽ P ) = ^Hxu, ⁽ P ) ^Hxu„ ⁽ P )•      (11)

Матрицы-строки для первой и второй частей системы регулирования, в которой действуют обратные связи как по среднему значению входного напряжения второй части преобразователя, так и по максимальному току магнитно-связанных дросселей, определяются из равенств (3) следующим образом:

(' + k c ) L 2 f_td П

FI(P)=--u----- вх

Q , ( P ) =- U²- [ ' 0 ];

вх

F , ( P ) =

'

K ( P ) K _u ( P ) Г

R T

;

(' + k_c ) L ₂ f_Kd n

1 ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^

U вх

Q ,, ( p ) = [ 0 0 ].

0      1

Передаточные функции К(р) и К _u (р) , учитывающие ДН и последовательное звено коррекции в прямой цепи регулирования, оставляем с теми же самыми, как и в (8), значениями К ₁ , К ₂ и Т ₁ , Т ₂ ,, Т ₃ , входящих в них, также рассчитывались в программе MathCad.

Наибольшую сложность вызывает определение матрицы [ рЕ -А _I - Н _I F(p) ] и ее обращение. Использование для операций с матрицами в символьном виде программного пакета MatLab, а также построение логарифмической амплитудной характеристики (ЛАХ), позволило получить результирующую ПФ замкнутой системы управления составного преобразователя (ввиду громоздкости выражений их здесь не приводим), соответствующую выражению (11) с учетом соотношений (4) – (7). Результаты моделирования

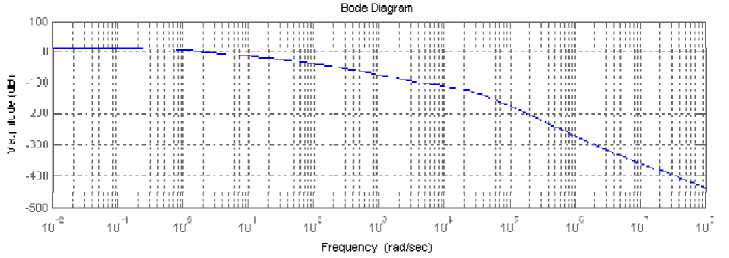
Рис. 5. Логарифмическая амплитудная характеристика замкнутой системы при воздействии входного напряжения и управлении по входу второй части составного регулятора и суммарному току

чувствительности выходного напряжения замкнутого преобразователя ко входному (рис. 5) показали более широкую полосу входных возмущений при действии обратной связи по току магнитно-связанных дросселей.

Таким образом, моделирование динамических характеристик на основе передаточных функций, полученных по вышеприведенным алгоритмам, показало следующее:

• 1.    Исследованы два из трех фундаментальных свойств статических преобразователей – устойчивость и чувствительность; для исследования инвариантности необходимы дополнительные структурные преобразования приведенной непрерывной линейной модели.

• 2.    Частоты резонанса полученных ЛАХ составного импульсного преобразователя соответствуют частоте колебаний его первой, повышающей части, причем значение частоты колебаний зависит от выбранной рабочей точки – заданного периодического режима преобразователя.

• 3.    Введение дополнительного внутреннего контура регулирования по суммарному току магнитно-связанных дросселей значительно улучшает параметры переходного процесса составного преобразователя.