Моделирование динамических процессов при прецедентном управлении автоматизированным насосным комплексом с учетом канала байпаса

А.Г. Лютов, , М.Б. Новоженин, , И.К. Шевцов, ,

A.G. Lutov, , Novozhenin, , I.K. Shevtcov, ,

При прецедентном управлении автоматизированными насосными комплексами (НК) [1, 2], реализующими технологические процессы перекачивания жидкостей во многих отраслях промышленности, необходим учет условий возникновения в НК нежелательных динамических процессов, в частности колебательных, наличие которых приводит к появлению различного рода нестационарных гидравлических процессов. Среди таких процессов наибольший ущерб вызывает кавитация [3–5], которая служит источником разрушения рабочих органов, шумам, вибрации и пульсациям давления в системе и, как следствие, снижению производительности, уменьшению КПД, повышению износа и уменьшению срока службы НК. Кавитация представляет собой серьезную проблему в связи с трудностью оперативного контроля ее возникновения и обеспечения безкавитационных режимов работы НК [6], которые включают в себя один или несколько насо- сов, а также всасывающий и напорные трубопроводы. Основное распространение получили НК с центробежными насосами (ЦН) по причине массогабаритных показателей, высокой производительности и способности перекачивать загрязненные среды [7].

В [ 1 , 8] предс т ав л е ны р е зу льтаты исследования условий возникнове н и я к ол еб ат ел ьны х про ц ес сов при а в т ом а тизирова н ном управлении НК при помощи прецеден то в бе з у че т а ка н а л а ба йп ас а. С п о с о б ре гули р ова н и я методом байпасирования, путем перепуска части жидко сти в о вса сыва ющ ую лин и ю н а сосов, предоставляет дополнительный кана л у п ра влен и я НК с пом ощь ю у п р а в л яемой задв иж ки. Это увеличивает пространство возможны х состоя н и й Н К как д и на м и ческ о г о объек т а и , с о отве т с твенно, расширяет возможности управления и форми р ова н и я пот е н ци аль н ы х п рец ед ентов при выборе рациональных (безкавита ц ион ных ) р е жим о в его работы.

Оп ре де ле н ие у с лов и й в озн и кновения колебательных процессов в НК для ра зли чн ых с п о с обов регулирования, в том числе и методом байпасирования, построение гра н и ц к о ле ба те льной у с той чи в ос ти и , в к он е чн ом и то ге, предоставление дополнительной коррект и ру ю щ е й и н форма ц и и для об о с н ов а н н ого в ы б ора прецедентов при автоматизированном управле н и и НК яв ляе тс я важной и актуальной задачей.

Напорно-р а с ход н а я ха р а кте ристика определяет изменение режима работы Н К . Т оч к а п ере с е ч е н ия хара к те рис ти к и с ети ( с у в е ли че н и е м ра с хо д а Q происходит увеличение и напора H ) и ха р а к те рис ти к и ЦН ( с у в е ли че н и е м расхода уменьшается напор) называется раб оче й точкой. Изме н ени е пол ож е н и я рабоче й точк и п рив одит к и зме нен и ю режи ма раб оты НК .

С ц е л ью и с сле дов а н и я д ин амических процессов в НК на основе методов теори и а в тома ти че ск ого уп ра в л е н и я п ри ме ни те л ьн о к линейным системам [9] необходима лине а ри за ц и я НРХ в области раб оч е й точк и . Вв е де м в рассмотрение дифференциальные сопротивле н и я д ля оп и с а н и я ди н а мичес к их п роц е сс ов в ок рес тн ос тях ра бочей т очк и НР Х:

R с

dH _c

d Q

Q ₀

> 0 ; R цн

dHцн dQ

Q ₀

< о ,

где Hцн – напор, развиваемый ЦН; Hс – напор гидравлической сети; Q – расход жидкости в системе; Rс – дифференциальное сопротивление сети; Rцн – дифференциальное сопротивление

ЦН (рис. 1).

//

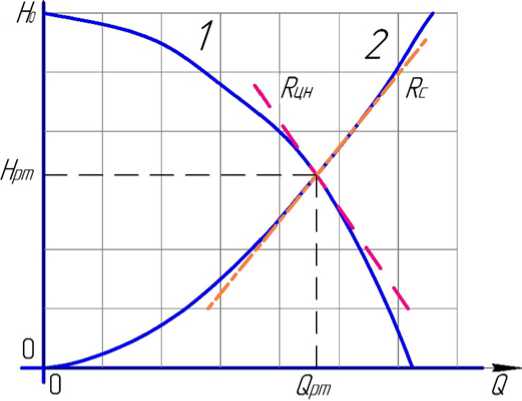
Рис. 1. НРХ ЦН (1) и сети (2)

Fig. 1. Pressure and flow characteristics of centrifugal pump (1) and network (2)

В с л учае п ри м ен е н и я пере п ускного канала как средства управления ре ж и мом ра б от ы р а с смот ри м с хем у п а ралл е л ь ног о вк л ю чени я, п ред ст авле н н у ю н а ри с . 2.

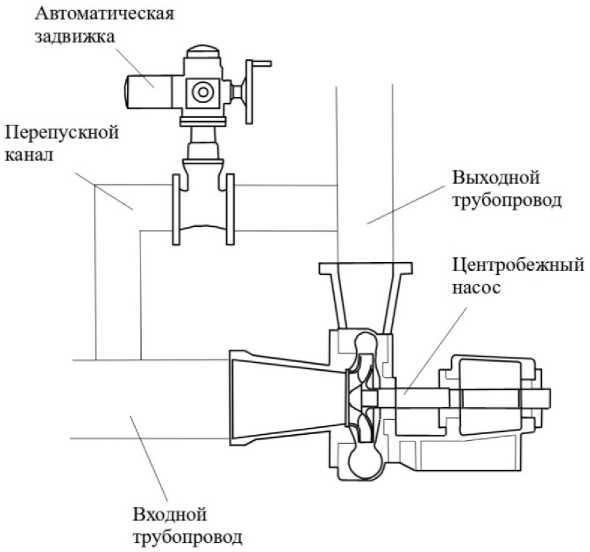
Рис. 2. Схема включения ЦН в НК

Fig. 2. Diagram of the centrifugal pump activation in the pump system

Структурная схема автоматизированной системы управления НК с применением прецедентного подхода [10] представлена на рис. 3.

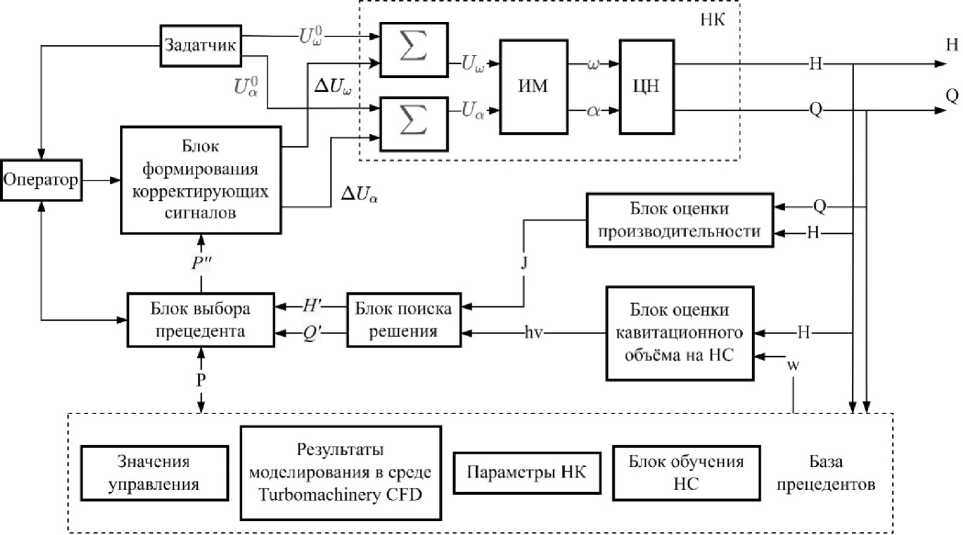
Рис. 3. Структурная схема системы автоматизированного управления НК с применением прецедентного подхода

Fig. 3. Block diagram of the pump system automated control system using the precedent approach

На рис. 3 имеются следующие обозначения: H – напор, развиваемый ЦН; Q – расход, развиваемый ЦН; ω – частота вращения ЦН; α – угол открытия задвижки на перепускном канале;

hv – объем кавитации; J – значение критерия оценки отклонения производительности (критерий оценки производительности); P - прецедент; P" - заключение о пригодности прецедента; w - веса настройки нейронной сети; H ', Q ' - теоретические значения напора и расхода ЦН в новой рабочей точке; U , , и ^{0 0} - управляющие воздействия по частоте вращения и углу открытия задвижки, формируемые задатчиком; A U _ю , A U _а - корректирующие воздействия по частоте вращения и углу открытия задвижки на перепускном канале соответственно.

Математическое моделирование

Метод электроаналогии [11], который получил широкое распространение также и при моделировании гидравлических процессов в НК [12–14], целесообразно использовать для построения динамической модели процесса перекачивания жидкости с целью анализа возникновения колебательных процессов.

В результате применения данного подхода была получена следующая модель НК (рис. 4).

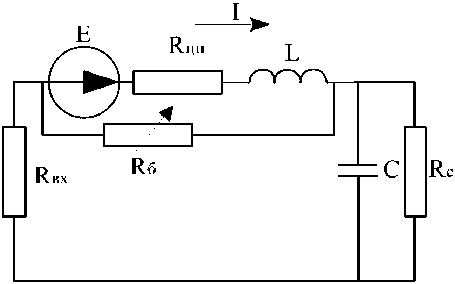
Рис. 4. Модель насосного комплекса, построенная на основе метода электроаналогии Fig. 4. Model of the pump complex, built on the basis of the electric analogy method

На рис. 4: E – электрический эквивалент напора, развиваемого ЦН; I – электрический эквивалент расхода; Rс , Rцн , Rвх , Rб – эквиваленты гидравлических дифференциальных сопротивле- ний сети, центробежного насоса, всасывающего (входного) трубопровода, байпаса с регулируемой задвижкой (соответственно); C – динамический элемент (электрическая емкость), отражающий упругие свойства жидкости и элементов конструкции насосного комплекса; L – динамический элемент (индуктивность), отражающий инерционность потока жидкости [12].

На основании 2-го закона Кирхгофа модель НК примет вид следующего уравнения электрической цепи в комплексной форме:

г г

R вх

E ( j ^{ю )} = I ( j ^{ю )} •

+-----c

R c Cj ю+ 1 J

Rc вх  Rc Cj ю +1

+ Rцн + j ю L

Выполнив преобразование Лапласа к операторной форме записи (p = jю), после арифмети- ческих преобразований получим:

E ( Р ) = I ( Р ) •

f ( R вх ( R c Cp + 1 ) + R c ) R б + ( R цн + Lp ) • ( ( R вх + R б )( R c Cp + 1 ) + R c ) )

( R вх + R б )( R c Cp + 1 ) + R c

Итоговый вид общей передаточной функции:

W_(p) = I ( p ) =__________________ ( ^R вх ⁺ R )( ^R c Cp ⁺ 1 ) + ^R c __________________

E ( p ) ( R вх ( R c Cp + 1 ) + R c ) R a + ( R цн + Lp ) • ( ( R вх + R 6 )( R c Cp + 1 ) + R c ) ^.

Анализ устойчивости динамических процессов

Устойчивость динамической системы, описываемой в окрестностях рабочей точки НРХ передаточной функцией (3), определяется параметрами ее знаменателя – характеристического полинома:

p2 [ CLRc (R вх + R б)] + p [ C (R б R вх Rc + R цн Rc (R вх + R6))+l (R вх + R б + Rc)] + б вх б c цн вх цн б цн c

К системам второго порядка применим критерий необходимого и достаточного условия устойчивости – положительность всех коэффициентов характеристического уравнения [9]. Коэффициент при p2 является безусловно положительным. Тогда для устойчивости системы необхо- дима положительность остальных коэффициентов характеристического полинома.

Условие устойчивости для среднего коэффициента:

C ( R б R вх R c + R _цн R c ( R вх + R б ) ) + L ( R вх + R б + R c ) > 0.                                       (5)

Предполагая, что значение L , отражающее инерционность потока жидкости, достаточно мало, то вторым слагаемым в (5) можно пренебречь:

C(-_бR_вxR _c + R h_H R_c ( R _BX + R )) >  0. вх c цн c вх

Кроме этого, если учесть, что C >  0 , то условие (5) примет следующий вид:

б вх c цн c вх б

Значения напоров ЦН и сети определим по графикам НРХ [15]:

H цн = Н о - aQ ²; Н с = bQ ².

В этом случае значения дифференциальных сопротивлений ЦН и сети будут:

R = — = -2aQ; R = — = 2bQ , цн dQ          с dQ а значения коэффициентов:

a =           ; b = Н с .

Q ²         Q ²

Учитывая то, что в рабочей точке Н _цн = Н _с = Н , получим следующее неравенство:

Н >  Н о

^{1 R} б ^R вх _Q

2 R вх + R б

При R₆ = да (байпас закрыт):

R

Условие (11) определяет колебательную границу устойчивости и выделяет области НРХ различной степени колебательности гидравлических процессов НК в окрестности рабочей точки (рис. 5). Область, расположенная выше границы устойчивости, соответствует устойчивым процессам, ниже – неустойчивым («в малом»).

Положительность значений свободного члена характеристического уравнения (4) передаточной функции исследуемой системы обеспечивается условием

R c R б + R c R ц н + R б R ц н + R в х R 6 + R в х R н >  0.                                             (13)

Полагая для удобства выкладок, что R 5 = k ( R _с + R _вх), где 0 <  к < да, получим неравенство

⁽ 1 + к ) R цн + к ( R c + R вх ) > 0.                                                                   (14)

Используя, аналогично вышеизложенному, полученные ранее выражения (9), (10), и с учетом того, что Н _цн = Н _с = Н , получим:

^H 0 ^{k R} вх ^Q

2   1 + к 4

Условие (15) определяет апериодическую границу устойчивости и соответствующие области НРХ (рис. 6). Области, расположенные выше данных границ, будут областями устойчивости, и, соответственно, наоборот: области, расположенные ниже данных границ, будут областями неустойчивости.

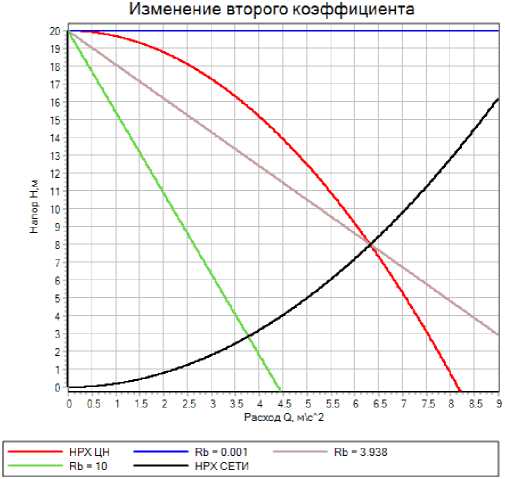
Рис. 5. Напорно-расходная характеристика центробежного насоса с колебательными границами устойчивости при различных значениях сопротивления байпаса R _b

Fig. 5. Pressure and flow characteristics of centrifugal pump with oscillatory stability limits at different values of bypass resistance R b

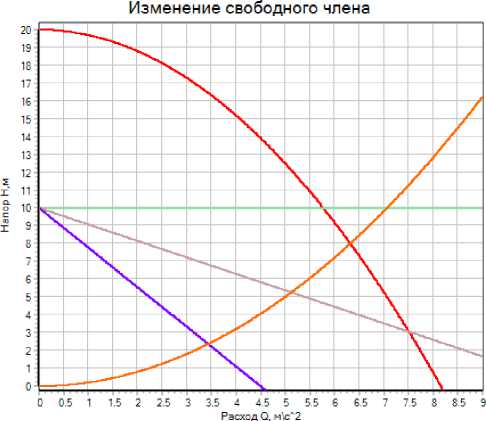
НРХЦН -------- Rb-0.001       ----- Rb-3.93В

Rb = 10   ------- НРХСЕТИ

Рис. 6. НРХ центробежного насоса с апериодическими границами устойчивости при различных значениях сопротивления байпаса R _b

Fig. 6. HP centrifugal pump with aperiodic stability limits at different values of bypass resistance R b

Анализ степени колебательности динамических процессов

Приведем передаточную функцию (3) к обобщенному виду передаточной функции второго порядка с учетом полинома числителя и соответственно:

E ( p )   a 2 p + a 1 p + a ₀

bo Г b a o I bo aa

² p + ¹ p + 1

a ₀       a ₀

p + 1

K ( T i p + 1 )

T 22 p ² + 2 ^ T 2 p + 1,

где bo = R х + Rб + Rc;

b = R c c ( R вх + R )

– коэффициенты числителя передаточной функции;

a o = R ( R вх + R c ) + R цн ( R вх + R + R c ) ;

a = R c C ( R вх R + R цн ( R вх + R ) ) + L ( R вх + R + R c ) ;

a 2 = R c CL ( R вх + R )

– коэффициенты знаменателя передаточной функции. Учитывая преобразования

K = b ^;

a ₀

b 1

T 1 = b o ;

T ₂

a ₂

a ₀

a ₂

T 2 = a    ;

a ₀

2- T2 = -1;  ^ = a0         2^/a0 • a2

получим следующие значения параметров передаточной функции (16):

K =          R вх + R6 + Rc

R б ( R вх + R c ) + R цн ( R вх + R 6 + R c ) ;

T = R c C ( R вх + R ) .

• ^{1    R} вх ^{+ R} б ^{+ R} c

  
  

T =           Rc CL (R вх + R6).

• ²    R^R б ( R вх + R c ) + R цн ( R вх + R б + R c ) ;

R c C ( R вх R 6 + R цн ( R вх + R 6 ) ) + L ( R вх + R 6 + R c )

• 2    V ( R б ( R вх + R c ) + R цн ( R вх + R 6 + R c ) ) • R c cl ( R вх + R 6 ) ^.

Как известно, уcловие 0 < ^ <  1 cоответcтвует области колебательных, а 1 < ^ - области апериодических динамических процессов [9]. Данные условия с учетом полученного выражения для ^ из (20) позволяют при необходимости выделить на НРХ области, cоответcтвующие разной степени колебательности гидравлических процессов в НК, а также области апериодических процессов.

Отметим, что уcловием нахождения коэффициента демпфирования ^ в области дейcтвитель-ных чисел является положительность подкоренного выражения для его определения (см. (20)).

Также, принимая, что H _цн = H _c = H в рабочей точке, выразим R _c и R y _н через коэффициенты напорно-расходной характеристики:

R c = 2 bpH^ ;                                                                (21)

V a + b

R _цн =- 2 aJ-HL- .                                                                (22)

V a + b

Численное моделирование

Был выполнен численный эксперимент, расчетные параметры которого представлены в таблице, с использованием динамической модели в виде передаточной функции (16) для иллюстрации характера переходных процессов в НК в различных областях.

Параметры для расчетов динамической модели Parameters for dynamic model calculations

Параметр	1-й эксперимент	2-й эксперимент 3-й эксперимент 4-й эксперимент
a	0,3
b	0,2
R б	0,001	3,93873	3,94	10
L	0,0013
C	0,1
R вх	100

Результаты численного моделирования динамических процессов в окрестности рабочей точки НХР с использованием программного пакета SimInTech для различных областей колебательности представлены на рис. 7.

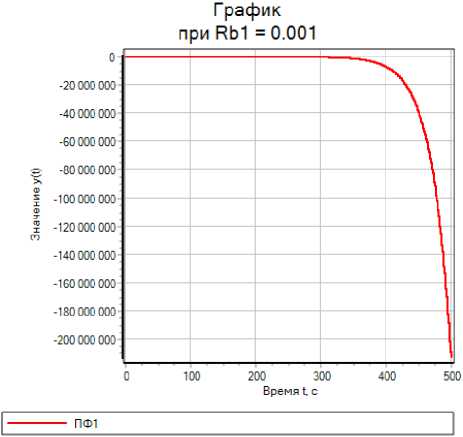
a)

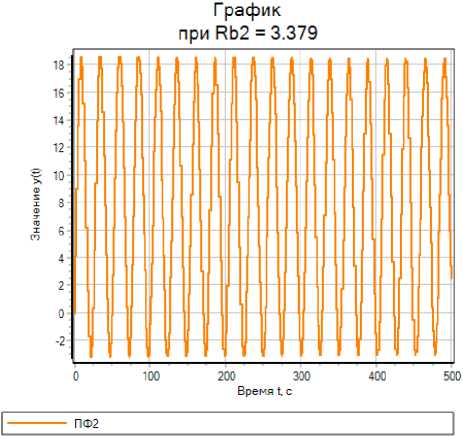
b)

Г рафик при Rb3 = 3.94

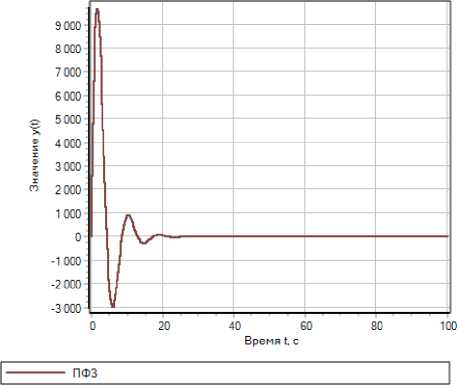
c)

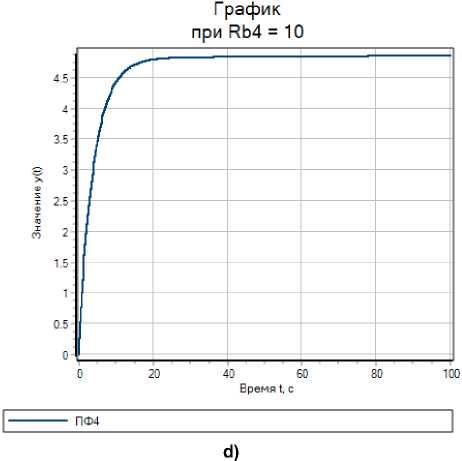
Рис. 7. Графики переходных процессов при различных условиях моделирования: a – в области апериодической неустойчивости; b, с – в области устойчивых колебательных процессов; d – апериодических (монотонных) процессов

Fig. 7. Transient plots under different modeling conditions: a – in the field of aperiodic instability; b, с – in the field of stable oscillatory processes; d – aperiodic (monotonic) processes

Обсуждение результатов

Структура динамической модели, выстаиваемой по методу электроаналогии, определяется схемой включения ЦН в НК. Анализ полученной динамической модели дает возможность на НРХ НК разграничить области, характеризующиеся разной степенью устойчивости и колебательности динамических процессов в окрестности рабочей точки НРХ. Это предоставляет дополнительную информацию при выборе прецедентов при автоматизированном управлении НК.

Для численного моделирования динамических процессов необходима идентификация параметров модели, таких как L , C , R вх , что может быть реализовано в том числе экспериментальнорасчетным путем.

Уточнение упомянутых границ областей НРХ возможно с использованием доверительных интервалов, при этом границы соответствующих областей будут иметь форму секторов.

Заключение

Полученные в процессе исследования результаты позволяют определить условия, при которых в НК на основе ЦН, оснащенных каналом байпаса, возникают колебательные процессы, способствующие возникновению или активизации нежелательных гидродинамических процессов. При этом данные условия находятся в зависимости от параметров НК – статических и динамических.

Для построения динамической модели НК использован метод электроаналогии. Это позволило провести анализ устойчивости и степени колебательности процесса перекачивания жидкости с использованием методов теории автоматического управления. Соответствующие аналитические зависимости и неравенства определили границы областей на НРХ с определенной степенью устойчивости, а также колебательности динамических процессов в НК.

Проведенные исследования осуществлены применительно к схеме включения ЦН в НК с использованием канала байпаса, что развивает методологию построения систем автоматизированного управления НК с применением прецедентного подхода, учетом характеристик динамических процессов с целью уменьшения или полного устранения различных нестационарных гидравлических процессов, в том числе кавитации.