Моделирование динамических режимов вибрационного робота, перемещающегося по поверхности с вязким сопротивлением

В статье представлены результаты исследования динамики мобильного вибрационного робота, безотрывно перемещающегося по поверхности с вязким сопротивлением за счет периодических движений внутренних масс. Особенностью рассмотренного устройства является то, что взаимодействие с поверхностью осуществляется при помощи опорных элементов, углом наклона которых к поверхности определяется модель силы вязкого сопротивления. Для движения объекта по заданному закону необходимо управлять величиной и направлением сил трения, что достигается перемещением внутренних масс по заданному закону.

Одно из достоинств такого вида систем заключается в отсутствии внешних движителей, что позволяет создавать устройства с гладким герметичным корпусом и использовать их для решения таких технологических задач, как мониторинг состояния окружающей среды, разведывание полезных ископаемых, взятие проб воды и воздуха в зонах, недоступных другим роботам, транспортировка грузов.

Закономерности и особенности перемещения вибрационных роботов, различных по конструкции, количеству и законам движения внутренних масс, изучаются многими отечественными и зарубежными исследователями. В работах [1 – 3] рассматривается прямолинейное движение двух- массовой системы в среде с сопротивлением, установлены законы движения внутренних масс, при которых объект перемещается с наибольшей за период средней скоростью. В [4] представлены результаты исследований влияния периодических относительных колебаний внутренней массы на характер перемещения робота, анализ которых позволяет определить условия для реализации движения системы в желаемом направлении. Перемещение вибрационного робота по горизонтальной поверхности за счет гармонических колебаний внутренних масс в горизонтальной и вертикальной плоскостях с одинаковой частотой и со сдвигом фаз исследовано в [5]. Математическая модель движения вибрационного робота по шероховатой горизонтальной плоскости предложена в [6], получены основные закономерности движения. В [7, 8] описываются особенности управления движением двухмассового вибрационного робота, в [9, 10] показаны способы управления направлением перемещения системы с тремя вращающимися массами. Исследование динамики плавающего робота, перемещающегося посредством периодических колебаний внутренних масс и асимметричной силы вязкого трения, создаваемой благодаря форме корпуса, приведено в [12]. В [13] для управления силой вязкого сопротивления используются

специальные элементы поплавков трехмассовой плавающей системы.

Особенностью вибрационных устройств является то, что их движение осуществляется за счет сил трения, возникающих при взаимодействии объектов с опорной поверхностью, поэтому сопротивление среды оказывает существенное влияние на динамику устройства, что нашло отражение в работах [1, 11]. В [1] рассмотрены линейный и квадратичный, изотропный и анизотропный законы сопротивления среды, в [11] представлены кусочно-линейное, квадратичное и сухое кулоново трение.

Математическая модель виброробота

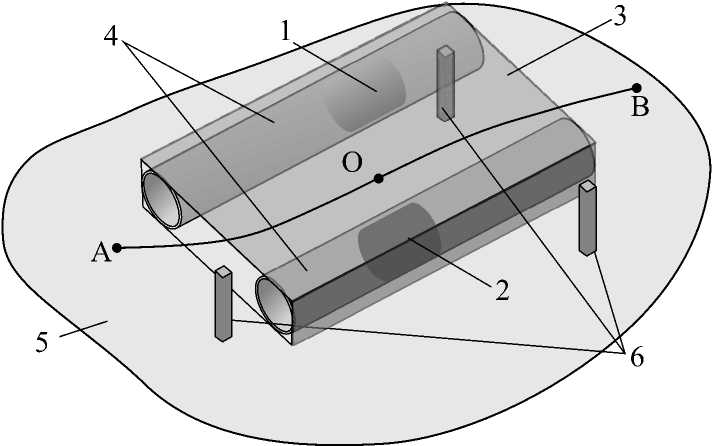
Рассматриваемый виброробот состоит из трех основных частей ( рис. 1 ): двух подвижных внутренних масс 1 и 2 ( m 1 и m₂ ) и корпуса 3 массой m . Внутренние массы перемещаются относительно корпуса по направляющим 4. Корпус взаимодействует с поверхностью 5, на которую нанесено смазывающее вещество, при помощи трех опорных элементов 6.

Движение робота по некоторой криволинейной траектории АВ осуществляется за счет сил трения, возникающих при перемещении подвижных масс в направляющих по заданным законам.

Для исследования движения вибрационной системы введем абсолютную неподвижную систему координат О₁х₁у₁ и относительную Оху , жестко связанную с корпусом робота, начало координат О которой совпадает с центром масс корпуса, ось Ох параллельна траекториям движения внутренних масс. Поворот системы координат Оху относительно О 1 х 1 у 1 определяется углом ϕ .

Будем считать, что корпус робота представляет собой абсолютно твердое тело, центр инерции которого расположен в точке О ( рис. 2 ). Внутренние массы 1 и 2 являются точечными и движутся по прямолинейным траекториям, которые расположены в плоскости Oxy , параллельны оси Ox и равноудалены относительно центра масс корпуса робота на расстояние b . Внутренние массы движутся по гармоническим законам A j (t), j = 1, 2 вида

Aj(t) = aj·sin(ωj·t + αj), (1)

где a j – амплитуда, ω j – круговая частота, α j – начальная фаза перемещения внутренней массы.

Робот взаимодействует с поверхностью в точках C i , i = 1, 2, 3 при помощи опорных элементов, являющихся абсолютно твердыми телами. Силы вязкого сопротивления возникают в точках С 1 и С 2 , трением в точке С 3 пре-

Рис. 1. Общий вид вибрационного робота

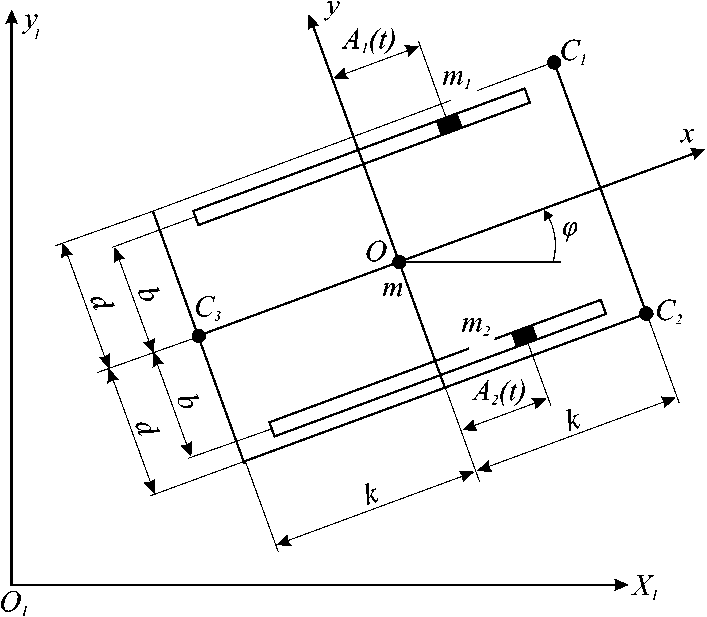
Рис. 2. Кинематическая схема робота небрегается. Модели этих сил вдоль осей относительной системы координат определяются углами наклона опор к осям Ox и Oy, а численные значения коэффициентов вязкости вдоль этих осей - углами наклона опор к осям Ox и Oy и свойствами смазывающего вещества.

Относительно положительного направления оси Ох i -ый опорный элемент может быть ориентирован под тремя углами γ_i , каждому из которых соответствует своя сила вязкости ( табл. 1 ).

Табл. 1. Зависимость силы вязкости вдоль оси Ох от угла γi

	γi = 90°	γi = 45°		γi = 135°
Q Cxi0	sr (0) - µ x0 x i	1	- 0 , xC) = 0 , -^"x®,^ >0, - MX" xC) , ,v < 0	1	1 " ■= 0 • _ max (.(О) < (0)     q P xG x Cj , xq > ", _ min . (0)   • (0)    n M x" x C; , x q <  0

В табл. 1 : x _C i — проекция скорости i -ого опорного элемента на ось Ох , µ _x ^{s r} ₀ , µ _x ^m ₀ ⁱⁿ , µ _x ^m ₀ ^ax – средний, минимальный и максимальный коэффициенты вязкости вдоль оси Ох .

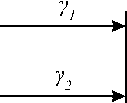
Угол наклона всех опор относительно оси Oy равен 900, поэтому вдоль нее возникает сила вязкого сопротивления, определяемая по формуле

ОУ

где Ц y0 — коэффициент вязкости вдоль оси О у , y 0 — проекция скорости i -ой опоры на ось Оу .

Зависимость коэффициентов вязкости от свойств смазывающего вещества проявляется в изменении численных зна-sr    min max чений параметров µ x 0 , µ x 0 , µ x 0 , µ y 0 при использовании различных веществ. Соотношение между коэффициентами вязкости вдоль оси Ох в i-ой точке опоры µx0i и вдоль оси Оу µy0 описывается формулой

r toj

α

Рис. 4. Структурная схема управляемой вибрационной системы

µx0i = µy0(1 + piχ)

где 0 ≤ χ ≤ 1 – коэффициент, зависящий от свойств смазывающего вещества,

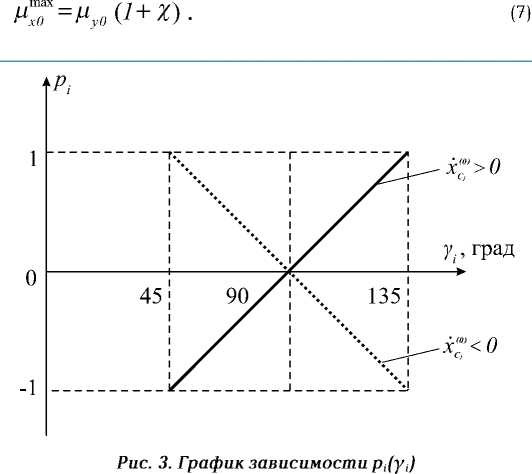
Р = 11Yi - 2 I sgn(x0)-V 45       >        ‘

параметр, являющийся функцией угла наклона опоры к положительному направлению оси Ох ( рис. 3 ).

При вертикальном расположении опорного элемента коэффициенты вязкого сопротивления вдоль осей Ох и Оу равны между собой:

sr

µ x = µ y .

При наклоне опорного элемента к оси Ох на углы γ_i = 45 и 135° значение коэффициента вязкого сопротивления µ_x0i может быть равно:

^min = ^ У о (1 - х),                                   (6)

Для движения вибрационного робота по требуемой траектории необходимо изменять модуль и направление сил трения, что достигается за счет управляемого перемещения внутренних масс и изменения ориентации опорных элементов. Структурная схема системы управления устройством показана на рис. 4 , где управляющими воздействиями являются углы γ₁ , γ₂ наклона опорных элементов в контактных точках С₁ и С₂ ; амплитуда а j , круговая частота ω j и начальная фаза α j движения j -ой внутренней массы. Координаты х и у центра масс корпуса устройства и угол ϕ поворота корпуса робота относительно его центра масс выступают в качестве управляемых параметров.

Дифференциальные уравнения движения объекта имеют вид:

.. ²         ..        ..                ..

j = i

• -Ф² ( A j cos Ф- B j sin Ф) + A j cos

  = Q_x1,

²              ..             ..

• -ф. ² ( A j sin ф + B j cos ф ) + A j sin ф ] = Q _y1 ,

j = 1

+2ф.AJAJ+ q)(A2 + B2)-AyB7] = Mo , где

В j = (–1)^j+1b – координата j -ой массы в проекции на ось Оу ; Q_x1 , Q_y1 – проекции главного вектора сил сопротивления на оси О₁х₁ и О₁у₁ ,

М_О – главный момент сил сопротивления, J – момент инерции корпуса.

Исследование характера движения робота

Задачей численного моделирования является выявление влияния на характер перемещения объекта параметров модели силы вязкого сопротивления и закона движения внутренних масс. Будем рассматривать два вида совместного перемещения внутренних масс m₁ = m₂ при a₁ = a₂ = a и

ω₁ = ω₂ = ω, отличающиеся начальными фазами: синфазное ( α₁ = α ₂ ) и в противофазе (α ₁ = α ₂ + π).

В результате проведенного исследования и анализа полученных графиков установлено, что при синфазном движении внутренних масс, одинаковой ориентации опор γ_1,2,3,4 = γ относительно вертикали и асимметричной силе сопротивления объект перемещается вдоль оси, совпадающей с продольной осью корпуса, в сторону меньшего коэффициента вязкости ( рис. 5 ).

При разной ориентации опор и противофазных колебаниях внутренних масс вибрационная система совершает вращательное движение относительно неподвижного центра масс корпуса ( рис. 6 ).

Программно-управляемое движение робота

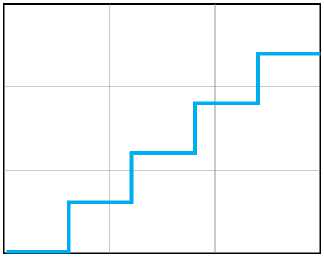
На основании проведенного анализа динамических режимов вибрационного робота разработан алгоритм ступенчатого перемещения устройства, заключающийся в чередовании участков прямолинейного и вращательного движений. Реализовать движение робота по различным криволинейным траекториям возможно путем варьирования времени прямолинейных участков и значений углов поворота корпуса ( рис. 7 ).

Исследование влияния коэффициента вязкости на среднюю скорость движения вибрационной системы

На рис. 8, 9 показаны зависимости средних линейных и угловых скоростей движения вибрационного робота от соотношения между минимальным и максимальным коэффи-min    max циентами вязкости µ x 0 / µ x 0 вдоль оси Ох для значений коэффициента χ = 0; 0,2; 0,3; 0,5. По графикам видно, что чи-

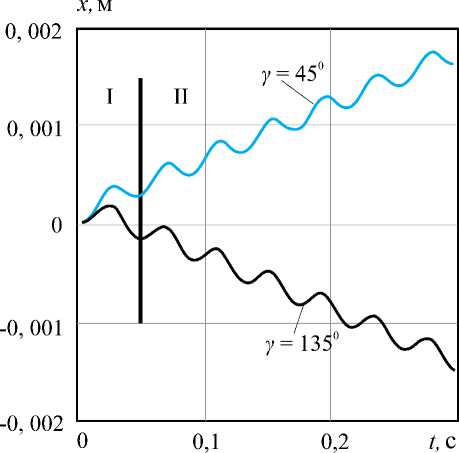
Рис. 5. Графики движения робота при синфазном перемещении внутренних масс:

I – переходный режим, II – установившийся режим

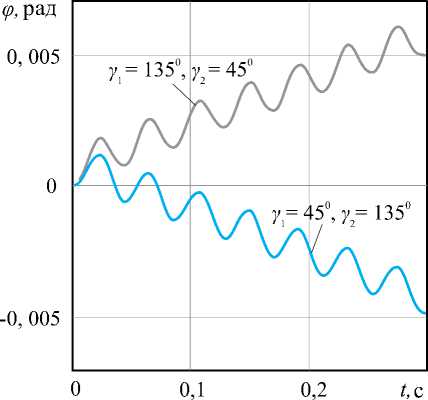
Рис. 6. Графики движения робота при перемещении внутренних масс в противофазе

V, м

О, 002

О, 001

О

м

a

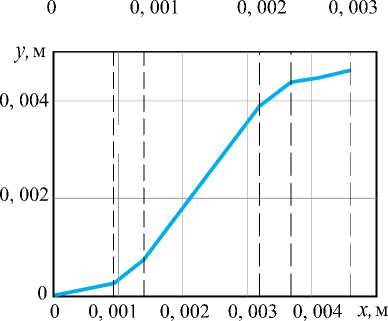
Рис. 7. Криволинейное движение виброробота: а – ступенчатое;

б – по s-образной траектории

б

сленное значение коэффициента вязкости при синфазном движении внутренних масс при γ = 45° не влияет на среднюю линейную скорость движения при χ = 0 , при χ ≠ 0 средняя линейная скорость x . _sr уменьшается с ростом соотношения µ _x ^m ₀ ⁱⁿ / µ _x ^m ₀ ^ax ( рис. 8 ). Причем, чем меньше коэффициент вязкости вдоль оси Ох , тем больше средние линейные скорости устройства при одинаковых значениях χ .

При разных углах наклона опор и противофазном движении внутренних масс с увеличением отношения минимального коэффициента вязкости к максимальному и с уменьшением коэффициента вязкости вдоль оси Oy средние угловые скорости уменьшаются при всех значениях коэффициента χ, кроме χ = 0 (рис. 9).

Выводы

В работе исследованы режимы управляемого движения трехмассового мобильного вибрационного робота, перемещающегося по горизонтальной плоскости в среде с вязким трением за счет периодических колебаний двух внутренних масс. Выявлено влияние модели силы вязкого сопротивления, ориентации опорных элементов и параметров законов колебаний внутренних масс на характер движения устройства. Реализовано программно-управляемое движение объекта по криволинейной траектории, которое заключается в чередовании участков прямолинейного и вращательного перемещений корпуса за счет управления углами наклона опорных элементов и сдвигом фаз колебаний двух внутренних масс.

min    max

Установлено, что с соотношения µ _{x 0} / µ _{x 0} , параметра χ и уменьшением коэффициента вязкости µ_y0 наблюдается возрастание линейной и угловой скоростей объекта

Работа выполнена в рамках гранта РФФИ проект 1.64.11 «Динамика управляемого движения вибрационных мобильных роботов по шероховатой поверхности по криволинейной траектории» № 11-08-01142.