Моделирование динамических волновых воздействий на примере массива сложноструктурных железистых кварцитов с использованием метода конечно- элементного анализа

В процессе работ, связанных с моделирование взрывомагнитных воздействий на массивы железистых кварцитов мы столкнулись с некоторыми трудностями использования известных программных пакетов (далее ПП). А именно, в основном берутся североамериканские стандарты систем единиц счисления. Формулы по которым работают модули изменить в большинстве случаев нельзя. Один ПП может и не содержать всех модулей для детального анализа, следовательно возникает ещё одна проблема – совместимость с ПП, которые содержат недостающие модули. Эти проблемы буквально вынудили знаться разработкой собственного ПП. В процессе обзора и анализа существующих методов, позволяющих решать поставленные задачи, явился метод конечно-элементного анализа.

Сам конечно-элементный анализ основан на методе конечных элементов, идея которого была заложена ещё в 1936 году советскими учёными для расчёта прочности элементов ракетной техники. Задачи прочности – задачи теории упругости. В МКЭ сплошная среда фрагментируется, т.е. вместо задачи теории упругости решается задачи сопротивления материалов. А эти задачи решаются достаточно просто. Т.к. элементов фрагментации получается довольно много, то всё это заносится в ЭВМ. Современными ПП решаются многие такие задачи.

В1943 году создан сам конечно-элементный анализ Р. Курантом, основанном на методе Ритца численного анализа и минимизации вариационного исчисления для получения приближенных решений к вибрации системы.

В1956 году Тренер, Клаф, Мартин и Топп создали более широкое определение метода.[2]

В1970 году бум активной разработки ПП на базе FEA и активное внедрение (в основном в армию США). [2]

Конечно-элементный анализ (FEA) состоит из компьютерной модели или некого «каркаса», который подчёркивает конкретные параметры для анализа (рис. 1). В FEA используется сложная система точек, узлов, которые образуют сетки. Эти сетки программируются так, чтобы они содержали свойства материала, его структуру, (например сложноструктурного массива железистых кварцитов).

_

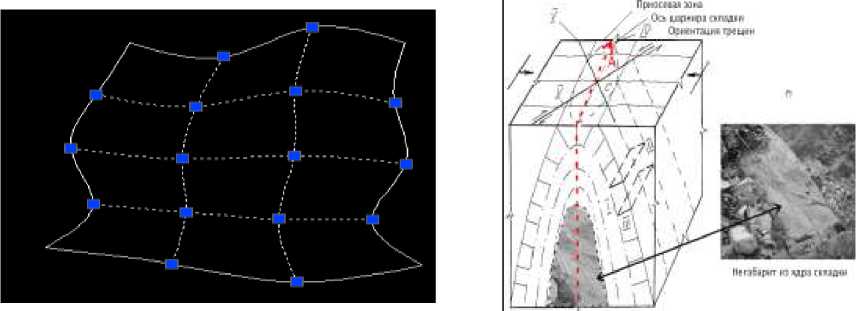
Рис 1 Сетка компьютерной модели для ядра складки сложноструктурного массива.

Существует широкий спектр целевых функций (переменные внутри системы): масса, объём, температура; параметры напряжённого деформированного состояния массива (НДС); скорость; синтетические параметры (определяющиеся пользователем); и т.д.

Также есть условия нагрузки, которые можно применить к системе: точка приложения нагрузки и т.д.

Каждая программа FEA, поставляется с элементом библиотеки, включающим в нашем случае: род элементов; упругие параметры; прочностные параметры и т.д.

В случае своместных комбинированных врыво-магнитных воздействий на массив — электродинамические параметры.

Метод FEA стал кульминационным для решения многих задач и сейчас находится в стадии развития. Пакеты FEA предлагают лишь маленькую часть того на что способен сам метод.

LS-Dyna применяется для моделирования взрывов и различных задач на упругость, но в этом ПП нет модулей для анализа электро-магнитных процессов в моделированной среде.

Comsol содержит ограниченную библиотеку и ошибки связности с MathCad.

На сегодняшний день код любой ПП FEA имеет закрытый характер, т.е. переписать элементы в модуле затруднительно при наличии ошиок в формуле или сама формула для расчёта не подходит, следовательно приходится ждать обновления или выхода новых модулей. ПП сопровождается недостаточной базой элементов с определённым набором параметров, которые расширить в большинстве случаев запрещается и множество дорогих малофункциональных модулей. ПП, которые могут использовать сразу несколько модулей очень дороги и далеко не каждая научная группа сможет позволить себе данное ПО.

На сегодняшний день стоит задача создания ПП с динамическими библиотеками и модульной структурой для дальнейшего развития техники и технологий горных работ.

В связи с этим предлагается ПП, состоящий из математического ядра со встроенным компилятором и модулями для 2D\3D визуализации. Также динамические библиотеки. Модули БВР и ГИС. Пользователю предлагается полная свобода действий как в разработке новых модулей, так и усовершенствования имеющихся. Для удобства взаимодействия и разработки, ПП поддерживает совместную работу через протокол TCP\IP.

Эти преимущества позволяют создать, с минимальной затратой сил и времени, такие модули, как: ГИС; БВР; геоэкологичиские; параметры горного оборудования; безопасноть ведения горных, взрывных работ и др..

Для удобства компилятор поддерживает следующие языки программирования: С, С++, Java и Fortran.

В качестве примере использования ПП разберём следющую задачу:

Имеется заряд тротила массой 1000 кг, помещённый в массив горной пароды над объектом (нарушение массива, трещина, неоднородность), расположенном на глубине 8 м от поверхности.

Объект представлял собой элемент массива. На глубине происходит подрыв заряда. Целью расчета являлось моделирование процесса, образования взрывной воронки, а также расчет кинематики и НДС (напряженно-деформированное состояние) элемента массива.

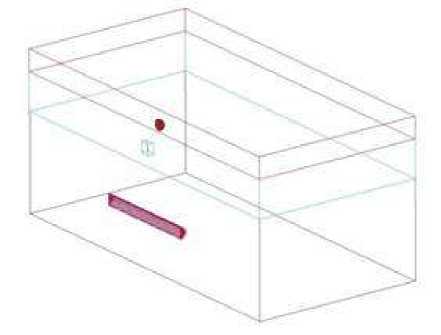
Рис. 2. Геометрическая модель.

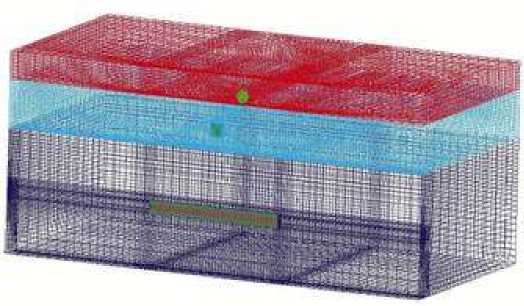
Рис. 3. Расчетная сетка сложноструктурного слоистого массива.

Механическое поведение верхнего слоя описывается упругопластической модель. Параметры условия пластичности рассчитывались по известным коэффициенту сцепления К = 0.3 МПа и углу внутреннего трения fi = fi/6 из условия (tокт/tmax)2 = 8/9 для предельных значений октаэдрического и максимального сдвиговых напряжений при одноосном растяжении . Объемная деформация принималась зависящей только от среднего нормального давления . В качестве исходного было использовано трехкомпонентное уравнение сжимаемости Ляхова.

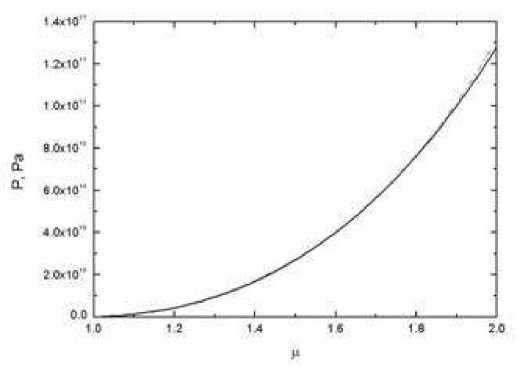
Рис. 4. Сжимаемость горной пароды

Элемент массива описывается моделью упругопластической среды с соответствующими кинематическими законами и параметрами.

Поведение продуктов детонации (ПД) тротила описывалось уравнением состояния JWL и гидродинамической моделью материала без учета вязкости. Детонация ВВ считалась мгновенной.

На втором этапе расчета моделировалось течение расширяющихся продуктов детонации (ПД), вызванное этим расширением течение грунта, а также рассчитывалась нагрузка на объект.

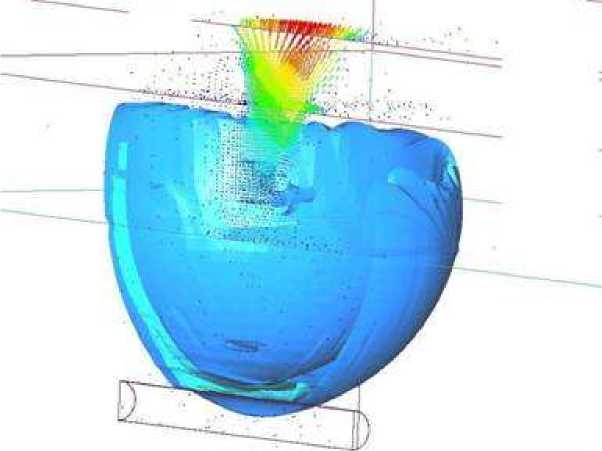
Рис. 5. Обтекание объекта ударной волной

В данной постановке взрыв происходил в скважине. На рисунке 5 показано распределение давления в массиве и направление векторов скорости ПД в момент обтекания элемента массива, представляющий собой полость(трещина) ударной волной.

Как видно из рисунка, значительная часть внутренней энергии взрыва переходит в кинетическую энергию ПД. В результате рост полости происходит за счет расширения канала без образования купола.

Для моделирования разномасштабных течений в работе была использована технология расчета на подвижной Эйлеровой сетке. Начиная с определенного момента, часть расчетной области пропорционально вытягивалась на заданное расстояние в сторону движения продуктов детонации и грунта. Бесконечно удаленная граница моделировалась заданием соответствующего граничного условия. Использование этих возможностей пакета позволило значительно сократить размерность трехмерной модели.

В начальный момент взрыва в массиве возникнет течение неустановившегося характера, связанное с распространением ударной волны. На рис. 6, 7 приведены профили давления и массовой скорости для двух точек на оси взрыва. Амплитуда ударной волны вблизи объекта составила 100 МПа.

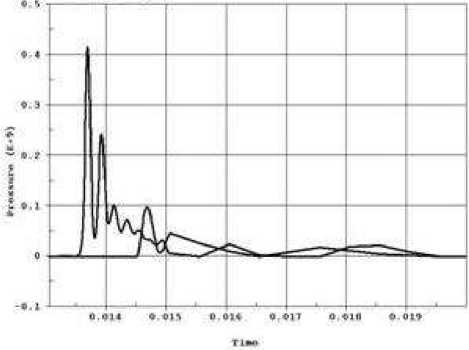
Рис. 6. Профили давления.

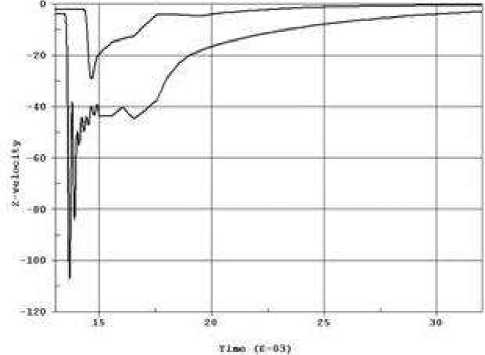
Рис. 7. Профили массовой скорости массива

Максимум нагрузки на элемент массива приходится на момент обтекания его ударной волной. Из-за кривизны фронта обтекание объекта волной начинается в центральной части и постепенно расширяется, что приводит к деформации элемента в центре. После ослабления воздействия накопленная энергия упругой деформации переходит в энергию связанных колебаний «полость-массив». По завершению обтекания элемента массива будет двигаться поступательно вместе с массивом и совершать при этом изгибные колебания.

На рис. 8 показаны деформированное состояние объекта в масштабе 1:50 и распределение напряжений по Мизесу в момент t = 0.017 c, которое соответствует изгибной форме колебаний. По результатам расчета пластическое состояние не достигалось.

В работе воздействие взрыва на грунт оценивалось по форме и размеру воронки. На рисунке 9 показано распределение плотности в различные моменты времени после взрыва. Видно, что в результате моделирования получена характерная форма воронки и ее края. Что касается достоверности моделирования разлета грунта в воздухе, то, поскольку взаимопроникание грунта, ПД и воздуха не учитывалось, начиная с некоторого момента времени можно говорить только о тенденции этого движения. По результатам работы глубина воронки составила 6 м, диаметр 12 м, что примерно в 2 раза меньше, чем параметры, полученные по инженерным формулам расчета. Как отмечалось выше, ослабление действия взрыва на массив связано с истечением ПД через скважину. В этом случае заряд необходимо рассматривать скорее как полузаглубленный.

Рис. 8. НДС объекта, t = 0.017 с.

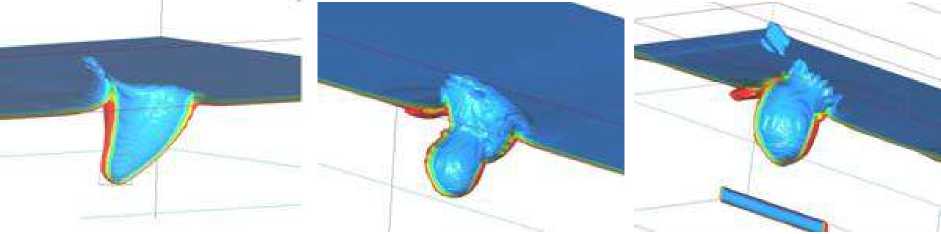
А                   б                   в

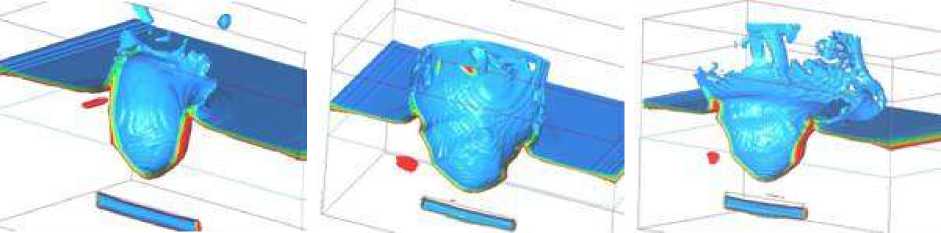
В                     г                     д

Рис. 9. Распределение плотности в различные моменты времени: a - t = 0.013 c; б - t = 0.015 c; в - t = 0.035 c; г - t = 0.065 c; д - t = 0.285 c; е - t = 0.513 c.

Такой программный комплекс, который мы предлагаем, позволяет рассчитывать не только отдельные виды физических полей, но и решать связанные задачи, например, учитывать взаимное влияние магнитного, теплового полей, поля механических напряжений, а так же решать задачи геодинамической и геологический безопасности, моделирование влияния крупномасштабных взрывов на окружающую среду и другие задачи специфики горно-рудного производства.