Моделирование динамического магнитного поведения ансамбля однодоменных частиц методом Монте-Карло

The Monte-Carlo method is used for modeling of dynamic behavior microclasters, consisting of not magnetic microsphere and located on its surface magnetic nano particle. In particular the phenomenon of a dynamic hysteresis of magnetization of system under the influence of a variable external field for cases of noninteracting particles, and as with the account an interaction dipole-dipolar is considered. From comparison of results of calculations of a method of Monte-Carlo with the exact numerical decision of the kinetic equation (for noninteracting particles) the estimation of intervals of the physical time corresponding to settlement steps of a method of Monte-Carlo is received.

Объединения магнитных наночастиц, возникающие в результате самосборки либо в процессе управляемого синтеза, представляют постоянную проблему для создателей качественных, стабильных магнитных жидкостей. В то же время подобные образования привлекают все большее внимание исследователей, рассматривающих задачи, требующие локальной концентрации магнитного вещества. В результате за последнее 10-15 лет было синтезировано большое число двух- и трехмерных вариантов подобных объектов: магнитных везикул [1], микроагрегатов [2] и микросфер [3-6] различных типов. В частности, хорошо развиты методы синтеза магнитных микросфер (ММС), позволяющие, используя разнообразные исходные материалы, получать объекты диаметром от сотен нанометров [4] до десятков микрон [3]. Следует заметить, что выше приводятся ссылки лишь на некоторые работы, посвященные данной теме, в то время как общий объем публикаций по ней не позволяет привести качественный литературный обзор в данной статье.

Повышенная концентрация частиц важна, например, в приложениях, связанных с гипертермией живых тканей, так как перераспределение магнитной фазы существенно меняет условия теплообмена на мезоскопическом уровне. Очевидно, что использование ММС наряду либо вместо отдельных наночастиц в качестве микрогенераторов, преобразующих энергию внешнего переменного магнитного поля в тепло, расширяет возможности магнитодинамических методов гипертермии. Даже не беря в расчет другие возможные приложения, уже эти задачи доказывают, что разработка и исследование микросфер составляют важное направление в развитии прикладной физико-химии сверхмалых магнитов.

Современные экспериментальные методы визуального наблюдения позволяют достаточно детально изучить морфологию полученных ММС, и, в частности, судить не только о внешней форме отдельных объектов, но и об особенностях структуры заполнения их поверхности. В то же время методы определения магнитных характеристик ММС, имеющих важное значение в задачах магнитоиндуцированного производства тепла, имеют на данный момент гораздо более низкую «разрешающую способность». На практике общепринятая и доступная техника наблюдения (включая SQUID) позволяет изучать лишь образцы, включающие многие тысячи микросфер. Кроме того, использование в гипертермии требует знания не статических значений характеристик системы, а их зависимости от амплитуды и частоты приложенного циклического магнитного поля. В этой ситуации компьютерное моделирование магнитных свойств ММС играет роль высокоточного инструмента, позволяющего «наблюдать» за поведением отдельного объекта (или системы из небольшого их числа): измерять его магнитную восприимчивость, коэрцитивную силу, кривые намагничивания и т.п.

Описание модели и метода

Типичная магнитная микросфера несет на своей поверхности (либо внутри себя) от десятков до сотен наночастиц. Даже если частицы являются однодоменными и не меняют своего положения в пространстве, а фазовое пространство системы включает в себя лишь ориентационные степени свободы (направляющие косинусы магнитных моментов частиц), то, все равно, при моделировании приходится рассматривать задачу с большим числом переменных. Поэтому было решено использовать для описания поведения подобных объектов метод Монте-Карло совместно с алгоритмом Метрополиса, хорошо себя зарекомендовавшими при решении задач с каноническим фазовым ансамблем. При традиционной реализации данной подход используется для поиска глобального минимума свободной энергии системы и определения основного состояния и равновесных характеристик ММС [7-8].

В то же время существует модификация метода Монте-Карло, позволяющая применять его и для описания неравновесных процессов. При таком подходе число шагов Монте-Карло рассматривается как «вычислительное» время, и делается предположение о том, что полученная в результате усреднения по реализациям последовательность состояний, которые система проходит в процессе расчета, близка к ее реальной фазовой траектории (см. например работу [9]). Решающим моментом такого расчета является оценка временного отрезка, соответствующего расчетному шагу (либо последова- тельности шагов) метода [10]. В настоящей работе рассматривается неравновесное намагничивание ММС и предполагается прямая пропорциональность между числом Монте-Карло шагов и физическим временем.

Рассмотрим магнитную микросферу, помещенную при заданной температуре Т в твердую немагнитную среду. На поверхности сферы располагаются без соприкосновения одинаковые однодоменные частицы с одноосной магнитной анизотропией. Позиции центров масс частиц и направления их «легких» осей распределены случайным образом. Магнитное состояние ММС описывается следующими безразмерными параметрами:

^ = ЦН / квТ, где ц - магнитный момент частицы, H - напряженность внешнего поля, кв - постоянная Больцмана;

а = Ea / к в Т ,

E A - величина энергии анизотропии;

Х = ц2/(квТ a3), где a - среднее расстояние между частицами - ближайшими соседями на поверхности ММС. В этих обозначениях максимальное значение квазистати-ческой коэрцитивной силы для частицы ^c = 2g.

В процессе расчета на каждом шаге магнитный момент одной из частиц поворачивался относительно своего текущего положения на случайный угол 8 с равномерным распределением из интервала [ -А , А ] . Далее вычислялась энергия ансамбля в новом состоянии, вероятность принятия которого оценивалась в соответствии со стандартным алгоритмом Метрополиса.

В работе [10] связь между числом шагов N и временем t определялась следующим образом. Сначала было найдено среднеквадратичное смещение 8 ²( А ) магнитного момента частицы на одном шаге Монте-Карло, затем эта величина сравнивалась с диффузионным смещением момента: 8 ² = 2 Dt . Здесь значение коэффициента и соответствующего характерного времени вращательной диффузии

D = 1/2т D, т D =ц(1 + а2)/2аукТ = t0g получены применением флуктуационно-диссипационной теоремы к линеаризованному уравнению Ландау-Лифшица-Гильберта, и использованы следующие обозначения: у - гиромагнитное отношение, а и т0 - соответст- венно параметр и характерное время затухания прецессии магнитного момента частицы. Далее авторы [10] оценивают средний интервал времени, соответствующего одному шагу метода Монте-Карло, из отношения

A t = б ²( А ) Id .

Важно отметить, что амплитуда вариация направления момента А должна выбираться такой малой, чтобы выполнялось условие б ² ^ 1, необходимое, в свою очередь, для того, чтобы можно было пренебречь влиянием полей (внешнего и анизотропии) на момент частицы на одном шаге метода. Поэтому оценка [10] по определению справедлива лишь для систем с относительно низкими энергетическими барьерами ( о< 1 ) и слабыми внешними полями ( ^ <  1 ) .

В то же время в большинстве рассматриваемых нами задач исследуются системы со значениями параметров о и ^ , существенно большими единицы. Кроме того, моделирование систем с высокими энергетическими барьерами за приемлемое расчетное время требует использования довольно больших амплитуд вариации направления магнитного момента: А ~ 1. Таким образом, гипотезы работы [10], как правило, не выполняются, и возникает необходимость оценки связи времени t и числа шагов N , подходящей для практических расчетов. С этой целью рассматривается циклический процесс намагничивания. Результаты, полученные методом Монте-Карло, сравниваются с численным решением соответствующего кинетического уравнения, при этом используются данные моделирования поведения системы при изменении внешнего поля за полный период.

Был рассмотрен динамический гистерезис намагниченности ММС во внешнем осциллирующем линейно-поляризованном магнитном поле с амплитудой ^ ₀ =^ _c . При моделировании непрерывно меняющееся поле ^ ₀cos to t заменялось последовательностью m этапов, со ступенчатым изменением поля между ними на величину А^ = 2 ^ ₀ / m . При этом на каждом этапе выполнялось одно и то же число шагов n метода Монте-Карло, а поле оставалось постоянным.

В качестве «эталонного» расчета использовались петли динамического магнитного гистерезиса, полученные из численного решения кинетического уравнения Брауна [11]. На рис. 1 представлена полевая зависимость нормализованной проекции (цz) / ц на направление внешнего поля. В расчетах методом Монте-Карло, проводившихся при постоянной амплитуде вариации А = const, рассматривались ММС, содержащие 103 наночастиц, у которых положения на поверхности сферы и направления осей анизотропии распре- делены случайным образом. Таким образом, единственным управляющим параметром метода было количество вычислительных шагов n, проводимых на каждом этапе моделируемого цикла. В табл. 1 приведены значения параметров расчета, а также оценка временного интервала At (в единицах т0), соответствующего одному шагу метода.

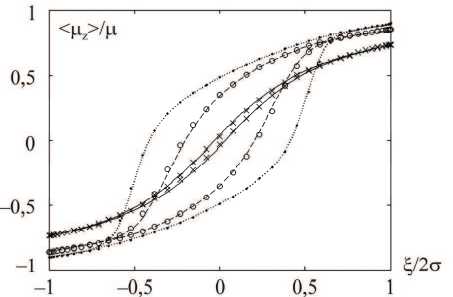
Рис. 1. Петли динамического гистерезиса намагниченности ММС с невзаимодействующими частицами с параметрами анизотропии о = 2 (кресты и непрерывная линия), о = 5 (пустые кружки и пунктирная линия) и о = 15 (закрашенные кружки и штриховая линия), помещенные в переменное магнитное поле с частотой ЫТ₀ = 10 ^{- 2} . Символы соответствуют результатам Монте-Карло-расчетов, линии - численному решению кинетического уравнения Брауна [11]

Таблица 1

Параметры Монте-Карло-расчета (результаты которого представлены на рис. 1) и оценка интервала времени, соответствующего одному расчетному шагу с амплитудой вариации A = 0,25

Параметры	о = 2	о = 5	о = 15
m	80
n	100	45	16
∆ t	0,08 т0	0,17 Т)	0,49 Т 0

Важным преимуществом применения метода Монте-Карло является относительная простота модификации модели для учета дополнительных усложняющих факторов, например диполь-дипольное взаимодействие между частицами. На рис. 2 представлено влияние величины параметра X на

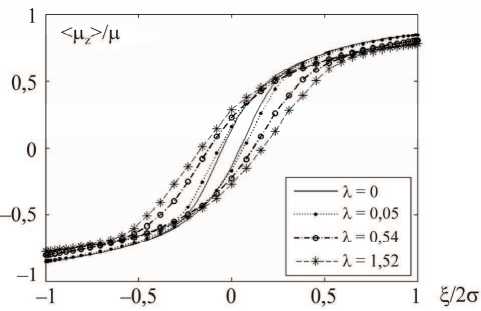
Рис. 2. Влияние диполь-дипольного взаимодействия на петли динамического гистерезиса намагниченности ММС, покрытых 100 (точки), 500 (пустые кружки) и 1000 (звезды) частицами, в поле частоты шт0 = 10-3. Сплошная линия соответствует результатам численного решения кинетического уравнения для системы без взаимодействия кривую циклического намагничивания. В расчетах рассматривались ММС с диаметром сердечника 200 нм, поверхность которых при однородном плотном заполнении в один слой может вмещать порядка 2 Х103 наночастиц размером 8 нм. Приведенные результаты, полученные для систем с числом частиц Np = 100, 500 и 1000, соответствуют случаям слабо- либо средне -заполненной поверхности сферы. Расчеты проводились для температуры 28 K и материальными параметрами, соответствовавшими маггемиту: MS = 400 Гс, K = 2 -105 эрг/см2. Как видно из рисунка, рост числа частиц приводит к увеличению площади петли гистерезиса, то есть к возрастанию остаточной намагниченности и коэрцитивной силы. Это можно объяснить, по нашему мнению, следующим образом. Под действием сильного внешнего поля моменты частиц выстраиваются преимущественно параллельно последнему. При случайном заполнении поверхности сферы всегда находятся частицы, расположенные так, что одинаковое направление моментов оказывается выгодным с точки зрения диполь-дипольного взаимодействия. Тем самым возникший магнитный порядок поддерживается даже при уменьшении внешнего поля.

Выводы

• 1.    Метод Монте-Карло с алгоритмом Метрополиса использован для моделирования магнитодинамического поведения микросферы, несущей на своей поверхности ансамбль суперпарамагнитных наночастиц.

• 2.    Полученные в расчетах петли динамического гистерезиса намагниченности системы, помещенной в осциллирующее магнитное поле с большой амплитудой, хорошо согласуются с результатами численного интегрирования соответствующего кинетического уравнения для случая невзаимодействующих частиц.

• 3.    На основе сопоставления этих двух подходов предложена и проверена процедура, связывающая число шагов метода Монте-Карло с физической продолжительностью процесса.

• 4.    Представлены результаты расчетов, показавшие существенное влияние диполь-дипольного взаимодействия между частицами на поведение системы.

Работа проведена при частичном финансировании из средств проектов РФФИ 08-02-00802, РФФИ-НЦНИ 09-02-91070 (PICS 7825), а также грантов Министерства образования и науки РФ № 02.740.11.0442 и AATP 2.1.1/4463.