Моделирование динамики армированных пологих оболочек из нелинейно-упругих материалов
Автор: Янковский А.П.
Статья в выпуске: 2, 2017 года.
Бесплатный доступ
Сформулирована задача динамического поведения гибких армированных пологих оболочек, изготовленных из нелинейно-упругих материалов фаз композиции. Армирование осуществляется перекрестно по поверхностям, эквидистантным срединным поверхностям конструкций. Структура армирования по толщине оболочек является квазиоднородной. Геометрическая нелинейность задачи рассматривается в приближении Кармана, а ослабленное сопротивление композитных конструкций поперечному сдвигу описывается соотношениями неклассической теории Редди, в рамках которой учитывается искривление поперечных нормалей к срединным поверхностям пологих оболочек. Численное интегрирование поставленной начально-краевой задачи осуществляется на основе метода шагов по времени с привлечением явной схемы типа «крест». Проведены конкретные расчеты динамического поведения относительно тонких и толстых пологих сферических оболочек и пластин, имеющих в плане кольцевую форму, при наличии жесткой внутренней шайбы и нагружении избыточным давлением, вызванным взрывной воздушной волной. Тонкостенные конструкции имеют жесткое закрепление по внешней кромке и осесимметричное армирование по логарифмическим спиралям в плане. Изучается влияние углов армирования на податливость и напряженно-деформированное состояние в материалах фаз композиции гибких пластин и пологих оболочек. Выявлено, что на множестве рассматриваемых структур армирования рациональным является армирование по радиальным (меридиональным) направлениям, так как такая структура обеспечивает минимальную податливость и наименьшее напряженное состояние в материале связующей матрицы композиции. Показано, что в силу геометрической и физической нелинейности исследуемой задачи динамический отклик композитных пологих оболочек существенно зависит от того, к какой лицевой поверхности (выпуклой или вогнутой) прикладывается избыточное давление взрывного типа.
Пологие оболочки, структуры армирования, динамическое деформирование, нелинейная упругость, геометрическая нелинейность, теория редди, взрывные нагрузки, схема "крест"
Короткий адрес: https://sciup.org/146211676
IDR: 146211676 | УДК: 539.4 | DOI: 10.15593/perm.mech/2017.2.13
Текст научной статьи Моделирование динамики армированных пологих оболочек из нелинейно-упругих материалов
PNRPU MECHANICS BULLETIN
Тонкостенные элементы конструкций типа пластин и оболочек из композиционных материалов находят все более широкое применение в инженерной практике [1–3]. Активное использование оболочечных конструкций объясняется их высокой эффективностью, так как они обладают легкостью в сочетании с высокой прочностью [4, 5]. Особенно ярко эта эффективность проявляется при внедрении в инженерные изделия композиционных оболочек волокнистой структуры [5–8], поэтому актуальной является проблема адекватного расчета механического поведения композитных панелей и оболочек как при квази-статическом, так и динамическом их нагружении [4, 5, 9, 10].
На сегодняшний день подавляющее число публикаций по проблемам механического поведения анизотропных и композитных конструкций базируется на предположении о линейно-упругом поведении материалов компонентов композиции [4–11]. Однако современные композиты могут быть изготовлены из материалов фаз, проявляющих неупругие или нелинейно-упругие свойства [12–15]. Анализ справочных данных [14, 15] показывает, что при расчетах в рамках линейно-упругого поведения материалов всех компонентов композиции уровень напряжений, возникающих при этом в высокопрочных армирующих волокнах, не превосходит, как правило, 10–20 % от предела их прочности, т.е. уникальные прочностные свойства арматуры используются весьма неэффективно. При неупругом или нелинейно-упругом деформировании материала связующей матрицы композита несущую способность волокон можно использовать практически полностью [16].
Известно, что при армировании композитных пластин и оболочек высокомодульными волокнами необходимо при изучении их механического поведения учитывать ослабленное сопротивление поперечным сдвигам [4, 5, 9–11]. Как правило, этот учет проводится в рамках теории Рейсснера [9, 10, 17, 18] или теории Редди [4, 5, 11, 16, 19, 20] (в русскоязычной литературе их называют первым и вторым вариантами теории Тимошенко [19]).
В монографии [9] на основе гипотез Рейсснера исследовалось динамическое поведение гибких тонкостенных элементов композитных конструкций, изготовленных из линейно-упругих материалов компонентов композиции. В работе [21] проводилось сравнение динамического поведения гибких композитных балок-стенок из линейно-упругих материалов, рассчитанного по классической теории и двум вариантам теории Тимошенко, причем показано, что результаты расчетов по теориям Тимошенко могут существенно различаться. В [16] на базе гипотез теории Редди в геометрически линейной постановке построена модель нелинейно-упругого деформирования армированных пластин, нагруженных статически. Однако динамическое поведение тонкостенных композитных конструкций из таких материалов до настоящего времени не изучалось.
Для численного интегрирования динамических задач механики деформируемого твердого тела используют как явные, так и неявные схемы шагов по времени. Из явных численных схем наиболее часто используются схемы типа «крест» [9, 21–23], так как они достаточно просто поддаются алгоритмизации [9], а из неявных схем наибольшее распространение получили методы Ньюмарка [24, 25].
В связи с вышеизложенным настоящее исследование посвящено моделированию в рамках теории Редди динамического поведения гибких армированных пологих оболочек, изготовленных из нелинейно-упругих материалов компонентов композиции. Моделирование производится на базе метода шагов по времени с привлечением явной численной схемы типа «крест».
1. Постановка задачи
Рассматривается пологая оболочка толщиной 2 h , с которой связана криволинейная ортогональная система координат xt так, что отсчетная поверхность Ox 1 x 2 ( x 3 = 0) совпадает со срединной поверхностью оболочки (| x 3| < h ); координатные линии х 1
и x2 совпадают с линиями главной кривизны отсчетной поверхности; ось x3 направлена ооооооооооо
ООООООООООО ^оо^оооооооо x1
ооооооооо о 0>
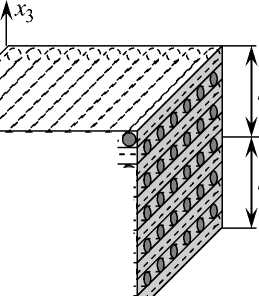
Рис. 1. Элемент армированной композитной пологой оболочки или пластины
Fig. 1. Element of the reinforced composite shallow shell or a plate
по толщине оболочки. Структура армирования конструкции в направлении x 3 квазиод-нородна. На рис. 1 изображен малый элемент пологой оболочки, причем искривленность отсчетной поверхности в силу ее малости не изображена.
Ослабленное сопротивление тонкостенного армированного элемента поперечному сдвигу будем учитывать в рамках теории Редди [4, 5, 11, 16, 19, 20], так как с точки зрения математического моделирования она является более точной [21], чем теория Рейсснера [9, 10, 17, 18]. Согласно теории Редди сдвиговые деформации в поперечном направлении s1 3 аппроксимируем по переменной x 3 так [4]:
£ i3 ( t , r ) = x^ + h £ ( + ) ( t ’ x ) - x^Th £ ( 3 ) ( t ’ x ) + hn ^x^ £ 0 ( t ’ x ) ’ 2 h 2 h h
x e G, x3| < h, t > t0, x = {y, x2}, r = {x^ x2, x3}, i = 1,2, где £(±), £03 - функции только двух пространственных переменных x1, x2 и времени t, подлежащие определению и имеющие следующий смысл: £(±) - деформации поперечных сдвигов на верхней (x3 = h ) и нижней (x3 = -h ) лицевых поверхностях оболочки, при £(±) = 0 функции £03 определяют деформации поперечных сдвигов на срединной поверхности x3 = 0 ; t0 - начальный момент времени; G - область, занимаемая пологой оболочкой в плане.
Согласно кинематической гипотезе теории Редди изменяемостью перемещений точек оболочки в направлении x 3 пренебрегаем, т.е. принимаем
U 3 ( t , r ) = w ( t , x ) , x e G , x з| < h , t > t 0 ,
где w - прогиб точек отсчетной поверхности x 3 = 0 .
На основании дифференциальных соотношений, связывающих деформации с перемещениями, с учетом (1) и (2) в приближении Кармана [4] для пологой оболочки получим
(V
U (t, r) = и (t, x)-x3dw +—3- h2 —- £03 + — — + h ^ —- — -h £(3), i = 1,2; (3) i x 7 / i x 7 / 3 i 72 n i 3 7 i 3 7 i 3 7 7 7 x / h у 3 у h у 2 у h у 2 у
9v (
£.. (t, r) = du. -x3d2w + —3- h2 —- d.£03 + — — + h d,^) —3 — -h 5.£*3) ++ ii у J ) ll 3 I 7 2 i i 3 7 I I i i 3 7 I i i 3r\ h у 3 у h у 2 у h у 2 у
+
1 V 2 (d w ) ,
£ 12 ( t , r ) = 1 ( d 1 u 2 +d 2 u 1 ) - x 3 d 1 d 2 w + 72 h 2 h
T2 A V
—3" (d^M + d2£03 + — x
3 JV 1 23 2 13 7 2 h
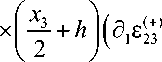
+ d 2 £ ( + )
-
x 3 ( x 3
2 h I 2
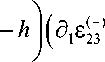
+ d 2 £ ( 3 )
) + ^ d 1 w 5 2 w ,
x e G , | x 3| < h , i = 1, 2,
где Ui - перемещения точек оболочки в тангенциальных направлениях xi ; ui - то же для точек срединной поверхности ( x 3 = 0 ); R i - главные радиусы кривизны отсчетной поверхности; d i - оператор дифференцирования по переменной x i ( i = 1, 2).
Таким образом, соотношения (1), (3) и (4) содержат следующие неизвестные функции: w , u i , £ ( j ) , £ 0 3 ( i = 1, 2), зависящие от двух пространственных переменных x 1 , x 2 и времени t .
Согласно принципу Даламбера, уравнения динамического равновесия пологих оболочек в приближении Кармана с учетом равенств (2) и (3) имеют вид [4]
F h 2 П/
У d . (f. - F3d,w] + —- + X tt, x) + о*3) -о(3) = 2hpu +—-(£*3) -£(3*),
J \ ij j 3 i ) T) i X 7 / 1 3 1 3 r i o\ i 3 1 3 7 7
j =1 R i 3
l = 1
d l
( A f„
Fn +У F,d w + -3
3 lJ J у J=1 у Rl
( + ) /T( - )
+ X 3 (t, x) + O’— - O’— = 2 h p w,
i = 1, 2;
2 .8 8
TA My- F i з + mi ( 1 , x ) + h ( a i 3) + a (3) ) = T h pl те , з -d W 1 + T h p ( E (3) + E (3) ) ,
j=1 3 V5
x g G, 1 > 10, i = 1, 2, где, согласно [14]
KK
P = Po“o + EP k“ k, “0 =1 -Eto k, k=1
p0, pk - объемная плотность материала связующего и арматуры k-го семейства; оk -плотность армирования волокнами k-го семейства; K - количество семейств арматуры; с(±) = ai3 (1, x, ± h) - заданные напряжения (поверхностные нагрузки) на верхней (+) и нижней (-) лицевых поверхностях оболочки; X, - приведенные внешние нагрузки, дей ствующие в направлении xi и порожденные объемными силами (i = 1, 3 ); mi - распределенные внешние моменты от объемных сил; Fi3 - поперечные силы; Fij - мембранные усилия; Му - изгибающие и крутящие моменты; точка означает частное дифференцирование по времени 1.
Материалы всех фаз композиции оболочки предполагаются изотропными и однородными, а их нелинейно-упругое поведение описывается тензорно-квазилинейными определяющими соотношениями [16, 26, 27]
a j * -8 X k ’ = g : * * ( е ! k ’ . Е k ) )( e j* > - jk ’ ) ( i , j = 1, 2, 3),
a - компоненты тензоров напряжений и деформаций в материале k-го компо- нента композиции (индекс k = 0 соответствует связующему, а индекс k = 1, 2, ..., K - арматуре k-го семейства); a0k), е0k) - среднее нормальное напряжение и средняя линейная деформация в k-м компоненте композиции; a Равенства (8) запишем в матричной форме [19]: ak = Ak8k, k = 0,1,2,..., K, где = f (k) (k) (k) (k) (k) (k)Г £ =f (k) (k) (k) (k) (k) (k)Г ak {a11 , a22 , a33 , a23 , a31 , a12 } , 8k {811 , е22 , 833 , е23 , 831 , е12 } , Ak = ( ay )) — симметричные 6 x 6-матрицы, ненулевые компоненты которых согласно (8) с учетом (10) определяются по формулам (24) из [27]; звездочка в верхнем индексе означает операцию транспонирования. Как и в [27], предполагаем, что определяющие соотношения (8) (а значит, и (9) с учетом (10)) удовлетворяют достаточным условиям сходимости метода последовательных приближений [26, с. 199], аналогичного методу переменных параметров упругости [29]. Поэтому далее в фиксированный момент времени t равенства (8) и (9) на текущей итерации считаем линеаризованными. В этом случае матричные соотношения (9) формально полностью совпадают с равенствами (22) из [27] (где ядра ползучести нужно принять тождественно равными нулю). Повторяя соответствующие рассуждения из [27], на данной итерации получим линеаризованные определяющие соотношения для армированной среды, записанные в матричной форме: а = Аг, (11) где а, г - шестикомпонентные векторы-столбцы средних напряжений и деформаций в композиции, имеющие структуру, аналогичную (10); А = (aj ) - известная 6 x 6-матрица, которую на текущей итерации можно трактовать как матрицу эффективных жесткостей армированной среды. Элементы aij матрицы A в (11) определяются из матричных соотношений (27) в [27] и зависят от деформированного состояния композиции гу, известного из решения на предыдущей Рис. 2. Локальная система координат, связанная с волокном k-го семейства Fig. 2. The local system of coordinates connected to a fiber of k-th family итерации, и от параметров армирования: плотностей юк и направлений армирования, определяемых углами сферической системой координат 0к и фк. На рис. 2 согласно [27] изображена взаимная ориентация глобальной xi и локальной xi(k) (i = 1,3), связанной с волокном к-го семейства, систем координат в случае пространственного армирования. Пусть из решения начально-краевой задачи для композитного тела (в частности, пологой оболочки), механическое поведение которого описывается определяющим соотношением (11), в текущий момент времени t на данной итерации известны осреднен-ные деформации е, тогда из матричных равенств (31) и (32) в [27] можно вычислить и деформации гк в к-й фазе композиции (9) и (10). После чего согласно методу после довательных приближений можно уточнить значения коэффициентов g*к) и g0к) в равенствах (8) (или, что то же самое, значения элементов матриц Ak в равенствах (9)) и по приведенному выше алгоритму (подробнее см.: [27]) можно определить следующее приближение решения и т.д., пока итерационный процесс не сойдется с требуемой точностью. В случае структуры армирования, изображенной на рис. 1 (6k=п /2 (см. рис. 2)) и рассматриваемой в настоящем исследовании, матрица A в соотношении (11) имеет такую структуру, что ее компоненты в 4-й и 5-й строках и в 4-м и 5-м столбцах, кроме диагональных, тождественно равны нулю, т.е. согласно обозначениям, аналогичным (10), имеют место равенства ° 23 a 44£23, °13 a 55£13. На основании силовой гипотезы теории Редди о33(t, r) * 0 [4, 5, 11, 16, 19-21] систему шести линейных алгебраических соотношений (11) с учетом (12) можно преобразовать к традиционному виду, исключив из рассмотрения приближение для деформации £33: где о = B£, ai3= bi£i3, i = 1, 2, a = {alpСТ22, a12} , 8={en, £22, £12} , £33 (a31£n + a32£22 )/a33 ’ bj = aj — ai3a3 j/a33, b3 = ai6, b3 j = a6 j , b33 = a66, b1 = a55, b2 = a44, i, j = 1,2, (15) aij - элементы матрицы A в равенстве (11); bj - элементы 3 x 3 -матрицы B; °, £j - компоненты средних напряжений и деформаций в композиции (элементы векторов-столбцов a и £ в равенстве (11)). Согласно (15) величины bj и bi в соотношениях (13) в текущий момент времени t предполагаются известными из решения рассматриваемой задачи на предыдущей итерации метода последовательных приближений. Для удобства дальнейшего изложения введем в рассмотрение новые неизвестные функции Yi3 (t, x) = j £03 —Sw, отсюда £03 (t, x) = 5(yi3 +diw), i = 1,2.(16) Уравнения движения (6) с учетом (16) принимают вид £9VMi/ — F3 + mi( t, x ) + h (° ^ + ° n) )= 7hp(Yi3 +£ n) +£ n) ), x c G, t ^ t0, i = 1, 2. (17) j=1 Равенства (5) и (17) образуют систему уравнений движения рассматриваемой гибкой пологой оболочки, к которым следует добавить четыре силовых граничных условия на лицевых поверхностях (см. (13) с учетом выражений (1) и (15)): °(t, x)= b(t, x, ± h)£i3±) (t, x), i = 1,2, где левые части известны. (В рамках классической теории [4, 24, 28] и теории Рейсснера [9, 10, 17, 18] граничные условия (18) удовлетворить не удается.) Из равенств (18) получаем £(3±) (t, x) = a(±) (t, x)/bi.(t, x, ± h), i = 1,2.(19) Следовательно, в данный момент времени t текущие приближения деформаций поперечного сдвига на лицевых поверхностях пологой оболочки можно считать известными, так как приближения «эффективных жесткостей» bi согласно равенствам (15) предполагаются уже известными из решения, полученного на предыдущей итерации метода последовательных приближений. В дальнейшем функции a(+) считаем известными из (19) в каждый рассматриваемый момент времени. Используя соотношения (13) с учетом выражений (1), (4) и (14)-(16), на текущей итерации можем определить все внутренние силовые факторы в пологой оболочке: h 2 F = J °dxз = £ BS U A — J h i=1 —5C 152w + 5C.5^3 + 2C(3)5.s(3+)— 2C3)5.s(3—) + 4 4 1 4 l l • 13 I I 13 I I I 3 S w 1 V +BiV+9 Bi(dw) Ri2 B 5 5 3 ~ (d2 U1 +d1u 2 ) — 2I A3 34 C3 ld1d2 w34 C3 (d2 Y13 +d1Y 23 ) + +2C3+) (d 2s(+) h (+ ) — ) 3) e(3) B3 + d1£23 ) 2C3 (d2a13 +d1£23 )+2 d!wd2w, M= J Cx3 dx3 = Ё Ai dUi —h i=1 . W 1 . z_ x2 +A,---3 — A,. (5,w ) ' R 2 v ' i +2H3+)(d2s(+) h + d1e2+) Fi3 = J G 3 dx3 = -h где согласно (14) — E,. — 5H |52w+5H.5,.y/3 + 2H(3)5/s(3+)— 2H(—^„.s3) + (20) i i / i i i * i3 i i i 3 i i i 3 A3Z. 5.)_ 5„ 3""2"" (d2 U1+d1U 2 ) — 2 I E3 —4 H3 ld1d2 w34 H3 (d2 Y13 +d1Y 23 ) + I—2H3-(826;—> wy)3A 31 wз 2 w, 5 d/ (Y,-3 3 5, w) 3 d')£(33) — 8 i \ • 13 i / i 13 diTi—), i = 1,2, x e G, t > 10, F - {Fu, F,2, F2}, M - {M11, M22, M12}, Ai, Bi, Ci, C(+), Ei, Hi, H(+) - трехкомпонентные векторы-столбцы, элементы которых совпадают с компонентами i-х столбцов 3 х 3-матриц A = ( aji), B =( bji), C = ( cji), C(+)= (Cj±), E = (eji), H = (hi), H(+)= (hji+)) (i’ j = 1,3), определяемых на основании соотношений (1), (4), (13) и (20) так: h A = J Bx3dx3, —h h B = J Bdx3, —h h C - (b3^ h < h2 x3- dx,, 3 J 3 h E - J Bx32dx3, — h C(+) h B^xLI x3+ h | Л 2 h I 2 J —h h dx3, hh 2fx. H(+)- [ в-31 -3-±h Idx,, (22) 2 h ( 2 J 3 —h 4 3 h 7 2 2 h1 7 , Г , h — x ,(+) r , x ±h , • , А d. - b. t— dx,, d. = b.-------dx,, i = 1,2, У nAFH - Fdw w) = F jij j3i i j=1 2 Г 2 У n, F,. +У F.d w l l3ljj l=1 V j=1 J = F 1 n 3, M 11 n12 + M22 n 22 + 2M12n1 n2= Mnn, (M22 - M11) n1 n2+ M12( n12 - n 22 ) = MnT, n1 = cos a, n2= sin a, x ef, t > t0, i = 1,2 и кинематические (см. (2) и (3)) w(t, x) = w,(t, x), x er, t > to;(24) Ui (t, r) = U,i (t, r), x еГ, |xз| < h, t > to, i = 1,2(25) граничные условия, а также начальные условия в момент времени t = 10: w(t0, x) = u03 (x), w(t0, x)= v03 (x); Ui( t 0, r )= U0 i (r ) , Ui (t0, r ) = V0i(r ), x e G, xз| < h, i = 1, 2.(27) Здесь Г – контур, ограничивающий область G, занимаемую пологой оболочкой в плане; Fi – заданные на Г мембранные силы, действующие по направлениям xi ; Fn3 – заданная на контуре Г поперечная сила; Mnn, Mnт- заданные на контуре Г изгибающий и крутящий моменты; w, - заданный на Г прогиб; U,i - заданные на торцевой поверхности оболочки перемещения в тангенциальных направлениях x5; a - угол, задающий направление внешней нормали к контуру Г; u03, v03, U0i, V0i (i = 1, 2 ) - заданные в начальный момент времени t0 перемещения и скорости точек пологой оболочки. Согласно выражениям (3) граничные (25) и начальные (27) условия нельзя удовлетворить в каждой точке по толщине оболочки при произвольных зависимостях функций U,i, U0i , V0i от поперечной координаты x3 . В силу этого обстоятельства кинематические граничные условия (25) и начальные условия (27) подобно силовым граничным условиям (23) будем удовлетворять в интегральном смысле, т. е. проинтегрируем равенства (25) и (27) по толщине оболочки с весами 1 и x3 , тогда с учетом соотношений (3) и (16) получим h2 2hu(t, x) + у 8i +) (t, x) h2 у 8(3-)( t, x) = u,( t, x) , 3 h [yi 3 (t, x ) + 8 (3) (t, x ) + 8 (3) (t, x )] = u, i (t, x), x еГ, t > 10, i = 1,2; h2 2hu; (tn, x) + 8(,) (tn, x) i03i30 h2 (-)/ у 8 i 3 ( t 0, x ) = u 0 i ( x ), 3 h3[y,-3 ( t0, x) + 8(3+)( t0, x) + 8i3-)( t0, x)]= u0i ( x), h2 2hHi( t 0, x) +у [8i3 ) ( t0, x)-8i3) ( t 0, x)] = v 0i( x) , 3 h3 [Yi3 (t0, x) + 8(3+) (t0, x) + 8i3-) (t0, x)] = v)i (x), x e G, i = 1, 2, где hhh u, i (t, x )=J U, i (t, r) dx3, u, i (t, x )=J U, i (t, r) x3 dx3, u 0 i (x )=J U0 i (r) dx3, - h - h - h hh u0 i ( x ) = J U0 i ( r ) X3 dx3 , v0 i ( x ) = J Vo i ( r ) dx3 , - h - h h v0 i ( x ) = J V0 i ( r ) x3 dx3 - h i = 1, 2. Таким образом, для однозначного интегрирования исследуемой динамической задачи в каждой точке области G в момент времени t0 должны быть заданы начальные условия (26) и (29) с учетом (30), а в каждой точке контура Г – силовые граничные условия (23) или кинематические граничные условия (24) и (28) с учетом (30). Возможно задать и пять смешанных из (23), (24) и (28) граничных условий, например в случае свободного опирания кромки пологой оболочки. После подстановки внутренних силовых факторов (20) с учетом (21) в уравнения движения (5), (17) и в силовые граничные условия (23) получим систему разрешающих уравнений и соответствующие ей силовые граничные условия, записанные в кинематических переменных w, ui и уi3 (см. (16)). Эти соотношения громоздки, поэтому не будем их приводить, помня о том, что далее предполагается использовать явную схему численного интегрирования рассматриваемой динамической задачи, для реализации которой (схемы) не требуется использовать уравнения движения и силовые граничные условия, выраженные явно через зависимые переменные w, ui и уi3 (i = 1, 2).
2. Метод расчета Для численного интегрирования сформулированной в п. 1 начально-краевой задачи применим метод шагов по времени [9, 21–25, 27], т.е. будем разыскивать решение в дискретные моменты времени tn+1= tn + т (n = 0, 1, 2...), где т = const > 0 - шаг по времени. Предполагается, что в моменты времени tm известны значения функций mm m m w ( x ) = w ( tm , x ) , ui( x ) = ui( tm , x ) , Yi3 ( x )=Y i 3 ( tm , x ) , ^(^^ ( x ) ^ ^jз’ ( tm , x ) , (31) akl (r) = akl (tm, r), i = 1,2, j = 1,3, k, l = 1,6, m = n-1, n, x e G, x3| < h. Здесь akl - компоненты 6 x 6 -матрицы A в равенстве (11)), тогда по формулам (20) с учетом (15), (19), (21) и (22) в момент времени tn можем определить значения всех внутренних силовых факторов Fij , Mij и Fi3 , входящих в уравнения движения (5), (17) и силовые граничные условия (23). Далее для аппроксимации встречающихся производных по времени будем использовать центральные конечные разности [9, 21–23], что позволяет получить явную численную схему для интегрирования рассматриваемой динамической задачи. Согласно этому конечно-разностные аналоги уравнений (5) и (17) с учетом обозначений, аналогичных (31), примут вид 2 hp(n+1 „n.n-1А Л —7— w - 2 w + w = > т V ) I=1 n2n n n d Fn +У F,- 5, w + R,-1 F l l3 lj j l ll nnn (+) rr(-) I .^X 3 I ^J 33 ^J 33 , Э hr\ ( n +1 n n-1A -hp u;-2 u;+u; т к ) — / n n n \ n n n = У8Д F - F3 dt w | + R-1F3 + Xt + ^+) j ij j 3 I i i 3 I 13 j=1 к 7 - n G(-) ui 3 , — h3p fn+1 n n -1Л 2n n n Г n n —z- y—2Yi+Yi ^УЗ..M -F3 + m + h c*+) + c(-) 2 1i i j ij 13 i i 3 13 3т к ) j=1 к 7 , x g G, i = 1,2, n = 1,2,3..., (3—) где h Yi(t, x) = Yi3 +;iV +;(3), ui (t, x) = u/+7(£iV-;i3)), i =1,2 (33) Так как правые части в уравнениях (32) известны, из них с учетом (19), (31) и (33) n+1 n+1 n+1 можем определить неизвестные функции w , ui и уi3 в следующий момент времени tn+1. Строго говоря, при t = tn к системе (32) следует присоединить необходимые граничные n+1 n+1 условия (23), (24) и (28) с учетом обозначений, аналогичных (31). При известных w , ui и уi3 по формулам (1), (4) и (14) с учетом соотношений (16) и (19) можем вычислить средние деформации композиции nj во всех точках пологой оболочки при t = tn+1. Используя известные функции n j (i, j = 1, 2, 3), по формулам (31) и (32) из [27] в момент времени tn+1 можно определить текущие приближения для деформаций фаз композиции, а затем по формулам (24) и (27) из [27] можно вычислить и компоненты 6 х 6 -матрицы A в равенстве (11). При этом в каждой точке пологой оболочки требуется реализовать итерационный процесс, аналогичный методу переменных параметров упругости. Для начала такого процесса можно взять известные при t = tn матрицы, используемые в соотношениях (31), (32) и (27) из [27]. Это вполне оправданно при достаточно малом шаге по времени т. После окончания такого итерационного процесса известными при m = n и m = n +1 становятся все функции, указанные в (31), поэтому по предложенной схеме можно построить решение исследуемой задачи в следующий момент времени tn+2 и т.д. Структура левых частей уравнений (32) с учетом выражений (33) свидетельствует о том, что для начала расчетов по описанной выше явной численной схеме необходимо 0 0 0 знать значения как функций w, ui и уi3, известных из начальных условий (26) и (29) 1 1 1 с учетом (19) и (30), так и функций w, ui и уi3 (см. (32) и (33) при n = 1 и t = t1). Значения этих функций получим, используя формулу Тейлора и учитывая начальные условия (26), (29) и уравнения движения (5) и (17) при t = 10 [22, 23]: 1 0 0 т2 0 ui ( x) = ui ( x) + т uti ( x) + у u ( x) + O (т3) ~ 0, 1 0 0 т2 0 Yi3 (x) = Yi3 (x) + туi3 (x) + у уi3 (x) + O(т3) ~ 0, w (x ) = w (x ) + т w (x ) + ^2- w (x) + O (т3)~ 0, i = 1,2, x g G, где приближенные равенства выполняются с точность порядка т3, а нулевые правые части соответствуют естественному состоянию, когда в начальный момент времени t0 пологая оболочка покоится и внешние нагрузки отсутствуют. Если область G, занимаемая пологой оболочкой в плане, является прямоугольной, то, аппроксимируя в уравнениях (32) производные 5i (•) по пространственным переменным xi их конечно-разностными аналогами, получим в конечном счете явную численную схему типа «крест» [9, 22, 23]. Если же область G является неканонической, то дискретизацию уравнений (32) по пространственным переменным xi (i = 1, 2) можно провести на основе вариационно-разностного подхода, использованного в [9], где показано, что для тонкостенных элементов конструкций необходимые условия устойчивости схемы типа «крест» определяются неравенствами, вытекающими из условия Куранта–Фридрихса–Леви [22]: Ae / т> ae, 2h I т> a3, (35) где ae = 7 Eee 1 P, a 3 = VE33 1 P, (36) p определено первым соотношением (7); Ae - максимальный размер ячейки дискретизации области G в направлении вектора e, параллельного отсчетной поверхности пологой оболочки; Eee, E33 – эффективные модули упругости первого рода в направлениях e и x3 , которые определяются с использованием компонент матрицы эффективных податливостей композиции, обратной матрице A (см. равенство (11) при линейно-упругом поведении материалов фаз композиции оболочки) [19]. Так как первое неравенство (35) должно выполняться при любом направлении e, для неоднородных, а тем более и криволинейных структур армирования пологих оболочек выбор шага по времени τ из условий (35) представляет самостоятельную трудоемкую задачу. Однако нетрудно показать, что если для каждого компонента композиции выполняются неравенства, аналогичные (35), то автоматически выполняются и условия (35) для армированной пологой оболочки. В силу этого далее используем именно такой необходимый критерий устойчивости предложенной явной численной схемы. Используя известные формулы перехода от декартовой прямоугольной системы координат к цилиндрической [30], полученные выше уравнения и граничные условия можно записать в полярной системе координат. Это удобно, если пологая оболочка является, например, сферической (что часто встречается в инженерной практике [31]), а область G представляет собой круг, кольцо или сектор круга либо кольца.
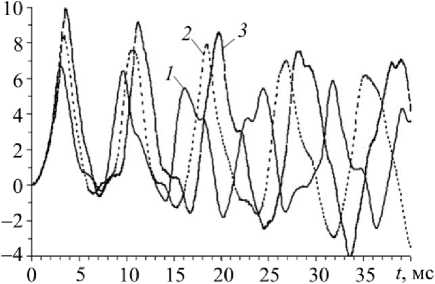
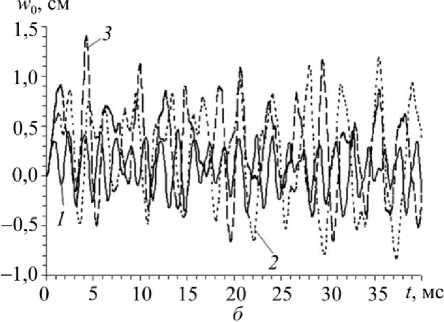
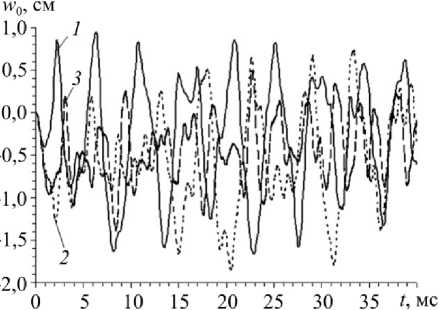
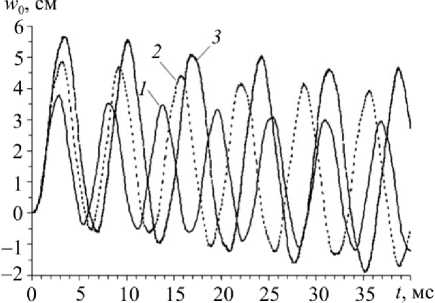
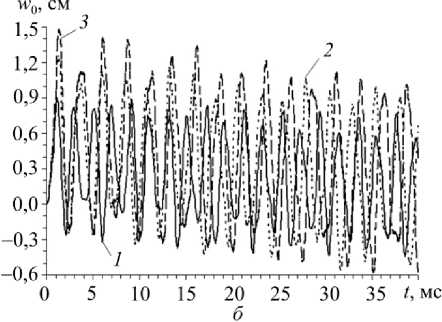
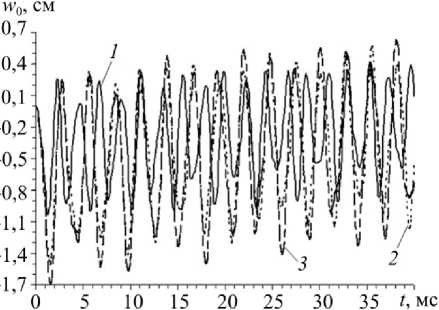
3. Обсуждение результатов расчетов В качестве конкретных примеров рассмотрим динамическое поведение пологих сферических оболочек (R1 = R2 = R ), для которых область G является кольцом, ограниченным контурами радиусов r0= 10 см и r1 = 60 см. Оболочки имеют постоянную толщину 2h = 1 см или 2h = 5 см и разные величины подъема стрелы f полюсных точек над их внешними опорными контурами (x1 = r1, где х1 - полярный радиус). Из геометрических соображений получаем R = Гу + f" 2f 0 < f< 2Г Объемными нагрузками пренебрегаем, т.е. Xi = 0 и mj = 0, i = 1, 3 , j = 1, 2 (см. (5), (6), (17) и (32)). Касательные нагрузки на лицевых поверхностях оболочки отсутствуют (о(±) = 0), поэтому из (19) следует а(±) = 0, i = 1, 2. Конструкции нагружаются фронтальной нагрузкой, порожденной воздушной взрывной волной (см. (5)) [24]: о(+) -о(-) = п(Л = * о33 о33 _ p (t ) Рmaxt / tmax, 0< t< t _ Рmax eXP ["«( t — tmax )] , max , , t > tmax , где tt = - ln(0,01)/( tmin - tmax )> 0, tmin » tmax, (39) tmax — момент времени, в который нагрузка p (t) достигает максимального по модулю значения pmax; tmin - момент времени, в который нагрузка p (t) по модулю становится пренебрежимо малой по сравнению с pmax (так, формула (39) соответствует случаю p(tmin) = 0,01 pmax). Согласно экспериментальным данным, приведенным в [24], в расче- Рис. 3. Кольцевая область, занимаемая пластиной или пологой сферической оболочкой в плане, с осесимметричными траекториями армирования по логарифмическим спиралям Fig. 3. The ring area occupied with a plate or a shallow spherical shell in the plan, with axial-symmetric trajectories of reinforcement on logarithmic spirals Предполагается, что пологие оболочки усилены осесимметрично по логарифмическим спиралям двумя (K = 2) семействами волокон с одинаковыми плотностями армирования (рис. 3), т.е. ®1 (х1 ) = ^2 (%!), Ф1 (%i) = -Ф2 (%i) = Ф = const, (40) r0< x1 < r1- Так как волокна имеют постоянные поперечные сечения [14], интенсивности армирования гоk в осесимметричном случае при укладке волокон по логарифмическим спиралям при любых углах φ определяются так [16]: гок (Х1 ) = r0®0к / %1, го0 к= гок( Г0 ) , ®01 =®02, к = 1,2, где го0к - плотность армирования волокнами к-го семейства, заданная на внутренней кромке оболочки x1 = r0. Из равенств (41) вытекает, что при любых углах армирования ф (см. (40)) общий расход арматуры в пологих оболочках фиксированных размеров при заданных значе- ниях ш0k будет один и тот же. В расчетах принимается ш01 = ш02 = 0,35 . В этом случае на внутренней кромке (x1 = r0) суммарная плотность армирования равна 0,7 (ш01 + ш02 = 0,7), что на практике соответствует предельно допустимому значению этой величины. Согласно (41) с удалением от внутренней кромки (x1 > r0) суммарная интенсивность армирования («1 (х1) + го2 (x1)) уменьшается и становится меньше предельно допустимого значения 0,7. Внешние кромки пологих оболочек предполагаем жестко закрепленными, т.е. в соотношениях (24) и (28) согласно (30) нужно принять w, = 0, и,i = 0, и,i = 0 (x1 = r1) и учесть, что 8(±) = 0, i = 1, 2. В отверстия же оболочек вставлены абсолютно жесткие плоские шайбы, которые жестко прикреплены к пологим оболочкам по их внутренним кромкам, т.е. имеют место условия сопряжения uiL-, = 0, bLr = 0, W (t) = 4-r, t ^ to, (42) I x = r0 lx! = r0 V ' 1x1 = r0 где w0 – осевое перемещение шайбы как жесткого целого в направлении x3 . При рассматриваемых типах нагружения (см. (38) и (39)), закрепления (см. (42)) и структурах армирования (см. (40) и (41)) в пологих оболочках реализуется случай осесимметричного изгиба, т.е. решения соответствующих начально-краевых задач не зависят от полярного угла x2 . Кроме того, поперечный сдвиг и тангенциальное перемещение в окружном направлении отсутствуют, т.е. у23= 0 и и2= 0. Чтобы в рассматриваемом случае замкнуть систему разрешающих уравнений (см. п. 1), необходимо использовать дополнительное уравнение движения жесткой шайбы, которое с учетом (38) имеет вид MW = пr2p (t) + 2пr0Fu (t, x )| , t > t0, (43) ' ' x x1 = r0 где M0 – масса шайбы; F13 – поперечная сила, определенная по формулам (20) на внутренней кромке оболочки (x1 = r0). В начальный момент времени t = 10= 0 конструкции находятся в состоянии покоя (см. (26) и (29) при и0i = 0, v0i = 0 , и0j = 0, v0j = 0, i = 1, 3 , j = 1, 2), а внешняя нагрузка отсутствует (см. (38)), поэтому справедливы соотношения (34). При замене в уравнении (43) второй производной по времени от w0 ее конечно-разностным аналогом исследуемая задача с учетом условий (42) может быть проинтегрирована численно по явной схеме «крест» (см. п. 2). Предполагаем, что нелинейно-упругая зависимость напряжения с от деформации 8 в каждом компоненте композиции оболочки при одноосном растяжении-сжатии характеризуется идеализированной диаграммой с линейным упрочнением [29]: Ekе, |=|<8S-=ask)/ Ek, sign(e)cSk) + Es(k) (е-sign(е)е^k)), |e| > 8(k), 0 < k < K, где Ek , Es(k) – модули Юнга и линейного упрочнения материала k-й фазы композиции; c(k), eSk) - напряжение и соответствующая ему деформация, при превышении которых материал ведет себя нелинейно. Физико-механические характеристики материалов фаз композиции пологих оболочек приведены в таблице, где v - коэффициент Пуассона. Характеристики материала связующей матрицы условно соответствуют эпоксидной смоле, отвержденной ароматическим аммиаком [15], а характеристики волокон – арматуре из L-стекла [14]. В последнем столбце таблицы указаны значения скорости звука a в материалах фаз композиции, вычисленные по формулам, аналогичным (36). Физико-механические характеристики материалов фаз композиции [14, 15] Physical and mechanical characteristics of the materials of the composition phase [14, 15] Материал р, кг/м3 ν os, МПа E, ГПа Es, ГПа a, м/с Связующая матрица 1210 0,4 20 2,8 1,114 1521,2 Армирующие волокна 4300 0,25 1500 51,0 10,851 3443,9 Для шайб условно примем р = 2710 кг / м3, что соответствует алюминиевым сплавам, а их толщины зададим вдвое большими толщин 2h соответствующих пологих оболочек. По этим данным можно рассчитать массы шайб M0 (см. (43)). При проведении расчетов вдоль полярного радиуса x1 (см. рис. 3) вводилась регулярная сетка с шагом Ах1 = (r - r0) /100 = 5 мм, а шаг по времени т = 1 мкс. На основании этих данных для первого неравенства (35) получаем отношение Ах1 / т = 5 км /с. Кроме того, в случае пологих оболочек рассматриваемых толщин (2h = 1 и 5 см) для второго неравенства (35) имеем 2h / т = 10 и 50 км/с. Эти отношения превышают значения a, указанные в таблице для материалов фаз композиции, поэтому необходимые условия устойчивости (35) используемой схемы «крест» выполняются со значительным запасом. На рис. 4 и 5 изображены зависимости w0(t), т.е. осцилляции жестких шайб, рассчитанные для пластин и пологих оболочек разной толщины, при разных структурах армирования и при разных уровнях динамического нагружения. Кривые 1, 2 и 3 на этих рисунках определены при углах армирования ф = 0, п /4 и п /2 соответственно (см. (40) и рис. 3, где изображен случай ф = п /4 - спиральное ортогональное армирование). На рис. 4 приведены результаты расчетов для относительно тонких (2h = 1 см , 2h / (r1 - r0) = 1/ 50), а на рис. 5 - для относительно толстых (2h = 5 см, 2h / (r1 - r0) = 1/10) композитных конструкций. Кривые на рис. 4, а и рис. 5, а характеризуют динамическое поведение шайб в случаях армированных пластин (f = 0 и R ^ да ), а на рис. 4, б и 4, в, а также на рис. 5, б и 5, в -в случаях пологих оболочек со стрелой подъема f = 0,2 м (см. (37)). Кривые на рис. 4, а и рис. 5, а определены при значениях pmax = 0,3 МПа и Рmax = 1,6 МПа соответственно, т.е. согласно (38) конструкции нагружаются избыточным давлением p (t) со стороны нижних лицевых поверхностей (х3 =-h ). Так как эти случаи соответствуют пластинам, изменение знака нагрузки p (t) при сохранении ее интенсивности приводит к тому, что кривые на этих рисунках зеркально отражаются относительно горизонтальной оси w0 = 0, поэтому такие кривые не изображены. Сравнение кривых с одинаковыми номерами на рис. 4, а и рис. 5, а показывает, что в случае относи- тельно тонких гибких пластин (см. рис. 4, а) шайбы совершают более сложные осцилляции, чем в случае относительно толстых конструкций (рис. 5, а). wo, CM Рис. 4. Осцилляции шайбы в случае относительно тонких композитных конструкций при трех структурах армирования: гибкой пластины (а); пологой оболочки, нагруженной снизу (б); пологой оболочки, нагруженной сверху (в) Fig. 4. Oscillations of the puck in the case of relatively thin composite structures with three reinforcement structures: a flexible plate (a); a shallow shell loaded from the bottom (b); a shallow shell loaded from the top (c) Кривые на рис. 4, б и рис. 5, б рассчитаны при pmax = 0,5 МПа и pmax = 3,4 МПа соответственно, т.е. при нагружении пологих оболочек избыточным давлением со стороны нижних (вогнутых) лицевых поверхностей (x3 = -h). Кривые же на рис. 4, в и рис. 5, в определены при pmax= -0,5 МПа и pmax= -3,4 МПа, т.е. при нагружении пологих оболочек избыточным давлением со стороны верхних (выпуклых) лицевых поверхностей (x3 = h ). Сопоставление кривых с одинаковыми номерами на рис. 4, б и рис. 4, в, а также на рис. 5, б и рис. 5, в демонстрирует, что в отличие от гибких пластин (см. рис. 4, а и рис. 5, а) динамическое поведение гибких армированных пологих оболочек, изготовленных из нелинейно-упругих материалов фаз композиции, существенно зависит от того, к какой лицевой поверхности (выпуклой или вогнутой) прикладывается избыточное давление p (t). Сравнение же кривых с разными номерами на каждом рис. 4 и 5 свидетельствует о том, что структуры армирования пластин и пологих оболочек, а точнее изменения углов армирования ф при фиксированном распределении плотностей армирования иk (см. (40) и (41)) существенно влияют на динамическое поведение этих тонкостенных композитных конструкций. Поведение кривых на рис. 4, а и рис. 5, а показывает, что в случае гибких пластин max |w0 (t)| достигается при первом локальном экстремуме зависимости w0 (t). Однако, например, поведение пунктирной кривой 2 на рис. 4, б свидетельствует о том, что в случае пологих оболочек max |w0 (t )| может достигаться и не при первом локальном экстре- муме зависимости w0 (t), т.е. динамическое поведение гибких композитных пологих обо- лочек является более сложным, чем гибких армированных пластин, изготовленных из нелинейно-упругих материалов компонентов композиции. Рис. 5. Осцилляции шайбы в случае относительно толстых композитных конструкций при трех структурах армирования: гибкой пластины (а); пологой оболочки, нагруженной снизу (б); пологой оболочки, нагруженной сверху (в) Fig. 5. Oscillations of the puck in the case of relatively thick composite structures with three reinforcement structures: a flexible plate (a); a shallow shell loaded from the bottom (b); a shallow shell loaded from the top (c) Во всех приведенных выше примерах максимальные значения интенсивности деформаций £(k) в компонентах композиций тонкостенных конструкций имели порядок 5 % и менее, поэтому все представленные решения, полученные на базе определяющих соотношений (8), являются вполне корректными с механической точки зрения. При этом наибольшие по модулю деформации возникают в связующем материале при окружном армировании (ф = п/2) пластин и пологих оболочек (см. штриховые кривые 3 на рис. 4 и рис. 5). Наилучшими же с точки зрения минимизации податливости и напряженно-деформированного состояния в компонентах композиции являются структуры с радиальным (меридиональным) армированием: ф = 0 (см. сплошные кривые 1 на рис. 4 и рис. 5). Выполненные расчеты показали, что при нелинейно-упругом поведении материалов фаз композиции для получения значений s*k) (k = 0, 1, 2 ) с точностью до трех значащих цифр на каждом шаге интегрирования по времени требуется делать до пяти итераций по методу переменных параметров упругости (см. п. 1 и 2). Заключение Проведенное исследование динамического поведения гибких композитных пологих оболочек и пластин, изготовленных из нелинейно-упругих материалов фаз композиции, продемонстрировало, что изменение направлений армирования существенно влияет как на податливость таких тонкостенных конструкций, так и на напряженно-деформированное состояние в материалах фаз их композиций, особенно в материале связующей матрицы. Следовательно, на множестве структур армирования целесообразно осуществлять поиск оптимальных или рациональных проектов армирования. В частности, для гибких пластин и пологих сферических оболочек, имеющих в плане кольцевую форму, при наличии внутренней жесткой шайбы наилучшим с точки зрения минимума податливости тонкостенной конструкции является армирование в радиальном (меридиональном) направлении. В силу геометрической и физической нелинейности рассмотренной задачи динамический отклик армированных пологих оболочек существенно зависит от того, к каким лицевым поверхностям (выпуклым или вогнутым) прикладывается избыточное давление взрывного типа, так как при этом значительно различаются не только амплитуды, но и частоты колебаний. Работа выполнена при финансовой поддержке РФФИ (грант № 17-01-00156-а).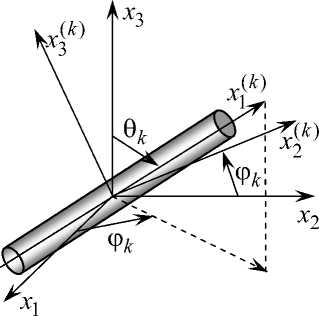
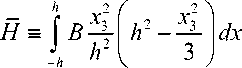
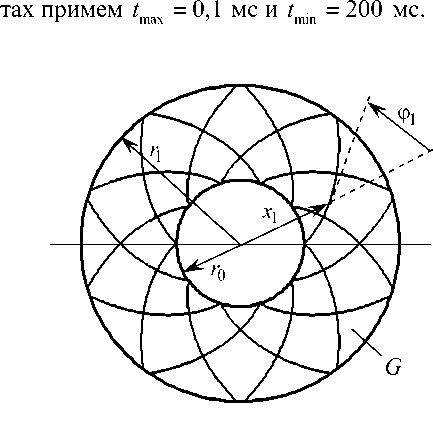
Список литературы Моделирование динамики армированных пологих оболочек из нелинейно-упругих материалов
- Review of advanced composite structures for naval ships and submarines/A.P. Mouritz, E. Gellert, P. Burchill, K. Challis//Compos. Struct. -2001. -Vol. 53. -No. 1. -P. 21-42.
- Bannister M. Challenger for Composites into the next millennium -a reinforcement perspective//Composites. -2001. -Part A 32. -P. 901-910.
- Gibson R.F. Principles of composite material mechanics/3rd ed. -Boca Raton: CRC Press, Taylor & Francis Group, 2012. -686 р.
- Амбарцумян С.А. Общая теория анизотропных оболочек. -М.: Наука, 1974. -446 с.
- Андреев А. Упругость и термоупругость слоистых композитных оболочек. Математическая модель и некоторые аспекты численного анализа. -Saarbrucken (Deutschland): Palmarium Academic Publishing, 2013. -93 c. Cao Z., Cardew-Hall M. Interference-fit riveting technique in fiber composite laminates//Aerospace Sci. and Technol. -2006. -Vol. 10. -P. 327-330.
- Muc A., Ulatowska A. Desing of plates with curved fiber format//Compos. Struct. -2010. -Vol. 92. -No. 7. -P. 1728-1733.
- Muc A., Muc-Wierzgoń M. An evolution strategy in structural optimization problems for plates and shells//Compos. Struct. -2012. -Vol. 94. -No. 4. -P. 1461-1470.
- Абросимов Н.А., Баженов В.Г. Нелинейные задачи динамики композитных конструкций. -Н. Новгород: Изд-во Нижегород. гос. ун-та, 2002. -400 с.
- Баженов В.А., Кривенко О.П., Соловей Н.А. Нелинейное деформирование и устойчивость упругих оболочек неоднородной структуры: Модели, методы, алгоритмы, малоизученные и новые задачи. -М.: ЛИБРОКОМ, 2012. -336 с.
- Белькаид К., Тати А., Бумараф Р. Простой конечный элемент с пятью степенями свободы в узле, основанный на теории сдвигового деформирования третьего порядка//Механика композитных материалов. -2016. -Т. 52, № 2. -С. 367-384.
- Maćko W., Kowalewski Z.L. Mechanical properties of A359/SiCp metal matrix composites at wide range of strain rates//Appl. Mech. Mater. -2011. -Vol. 82. -P. 166-171.
- Gill S.K., Gupta M., Satsangi P. Prediction of cutting forces in machining of unidirectional glass-fiber-reinforced plastic composites//Frontiers of Mechanical Eng. -2013. -Vol. 8. -No. 2. -P. 187-200.
- Композиционные материалы: справ./под ред. Д.М. Карпиноса. -Киев: Наук. думка, 1985. -592 с.
- Справочник по композитным материалам: в 2 кн. Кн. 1/под ред. Дж. Любина; пер. с англ. А.Б. Геллера, М.М. Гельмонта; под ред. Б.Э. Геллера. -М.: Машиностроение, 1988. -448 с.
- Янковский А.П. Упругопластическое деформирование изгибаемых армированных пластин при ослабленном сопротивлении поперечному сдвигу//Прикладная математика и механика. -2013. -Т. 77. -Вып. 6. -С. 853-876.
- Reissner E. The effect of transverse shear deformations on the bending of elastic plate//J. Appl. Mech. -1945. -Vol. 12. -No. 2. -P. 69-77.
- Шкутин Л.И. Нелинейные деформации и катастрофы тонких тел. -Новосибирск: Изд-во СО РАН, 2014. -139 с.
- Малмейстер А. К., Тамуж В. П., Тетерс Г. А. Сопротивление жестких полимерных материалов. -Рига: Зинатне, 1972. -500 с.
- Reddy J.N. Energy and Variational Methods in Applied Mechanics. -N.Y.: John Wiley, 1984. -604 р.
- Янковский А.П. Практическая устойчивость схемы «крест» при численном интегрировании уравнений динамики для гибких тонкостенных элементов конструкций, подчиняющихся гипотезам теории Тимошенко//Мат. методи та фiз.-мех. поля. -2015. -Т. 58, № 1. -С. 65-83.
- Рихтмайер Р., Мортон К. Разностные методы решения краевых задач. -М: Мир, 1972. -418 с.
- Самарский А.А. Теория разностных схем. -М.: Наука, 1989. -616 с.
- Houlston R., DesRochers C.G. Nonlinear structural response of ship panels subjected to air blast loading//Computers & Structures. -1987. -Vol. 26. -No. 1/2. -P. 1-15.
- Zeinkiewicz O.C., Taylor R.L. The finite element method. -Oxford: Butterworth-Heinemann, 2000. -707 p.
- Ильюшин А.А. Труды. Т. 3. Теория термовязкоупругости/сост. Е.А. Ильюшина, В.Г. Тунгускова. -М.: Физматлит, 2007. -288 с.
- Янковский А.П. Моделирование механического поведения композитов с пространственной структурой армирования из нелинейно-наследственных материалов//Конструкции из композиционных материалов. -2012. -№ 2. -С. 12-25.
- Трещёв А.А. Изотропные пластины и оболочки, выполненные из материалов, чувствительных к виду напряженного состояния. -М.; Тула: РААСН; Изд-во ТулГУ, 2013. -249 с.
- Малинин Н.Н. Прикладная теория пластичности и ползучести. -М.: Машиностроение, 1968. -400 с.
- Бидерман В.Л. Механика тонкостенных конструкций. Статика. -М.: Машиностроение, 1977. -488 с.
- Зубчанинов В.Г. Основы теории упругости и пластичности. -М.: Высш. шк., 1990. -368 с.


