Моделирование динамики частично насыщенных пороупругих тел на основе метода гранично-временных элементов
Автор: Игумнов Л.А., Петров А.Н.
Статья в выпуске: 3, 2016 года.
Бесплатный доступ
Дано описание математической модели частично насыщенной пористой среды, основанной на модели Био, с пятью базовыми функциями описания волнового процесса. В изображениях по Лапласу приведена математическая модель краевой задачи трехмерной динамической теории пороупругости. На основе теоремы операционного исчисления об интегрировании оригинала представлен шаговый метод численного обращения преобразования Лапласа. В качестве метода решения краевых задач трехмерной динамической теории пороупругости выбран прямой вариант метода граничных интегральных уравнений и приведено соответствующее граничное интегральное уравнение. Выписаны соответствующие матрицы фундаментальных и сингулярных решений трехмерной динамической теории пороупругости. Представлено краткое описание гранично-элементной дискретизации. Методическое обеспечение опирается на использование регуляризованного граничного интегрального уравнения, записанного с учетом преобразований симметрии задачи. Граничная поверхность исследуемого тела разбивается обобщенными восьмиузловыми четырехугольными элементами. Применяется согласованная поэлементная аппроксимация. Коллокационные точки решения граничного интегрального уравнения совпадают с узлами интерполяции неизвестных граничных функций. Для повышения точности интегрирования по элементу, не содержащему коллокационную точку, кроме формул интегрирования Гаусса, применяется также иерархический алгоритм интегрирования. Возникающие дискретные аналоги решаются методом Гаусса на основе шагового процесса получения значений граничных функций. Шаговый процесс определяется шаговым алгоритмом численного обращения преобразования Лапласа. Рассмотрена задача о скачке единичной поверхностной силы на торце призматического частично насыщенного пороупругого тела. В качестве пористого материала выбран песчаник. Для верификации гранично-элементной модели используется аналитическое решение соответствующей одномерной задачи. Проведено исследование решения задачи на сходимость по расчетной сетке, а также рассмотрено влияние параметра шаговой схемы на решение.
Пористая среда, модель био, преобразование лапласа, граничные интегральные уравнения, метод граничных элементов, шаговая схема, призматическое тело, аналитическое решение
Короткий адрес: https://sciup.org/146211631
IDR: 146211631 | УДК: 539.3 | DOI: 10.15593/perm.mech/2016.3.03
Текст научной статьи Моделирование динамики частично насыщенных пороупругих тел на основе метода гранично-временных элементов
PNRPU MECHANICS BULLETIN
Пористые материалы моделируются упругим скелетом, или матрицей, с неким распределением закрытых и открытых пор, содержащих жидкий или газообразный наполнитель. Примерами пористых материалов могут служить водонасыщенные грунты, горные породы, биологические ткани, пенометаллы и т.д. Механика пористых сред имеет большое значение во многих областях науки и техники, таких как геотехника, геомеханика, инженерная геология, биомеханика, машиностроение и материаловедение. В сейсмостойком строительстве важную роль играет прогнозирование потери прочности грунта в результате скачка порового давления жидкости, вызванного сейсмическим воздействием.
Началом исследований волновых процессов в насыщенных пористых средах послужила работа Я.И. Френкеля [1]. Л.Я. Косачевский [2] показал, что теория М. Био [3,4], как и подход Я.И. Френкеля, опирается на те же соотношения между напряжениями и деформациями, но отличается большей общностью. Естественным продолжением этих работ стали попытки различных авторов обобщить теорию на случай пористых сред, насыщенных двумя несме-шивающимися текучими наполнителями. Принципиальным отличием в данном случае является необходимость учитывать поверхностные натяжения и капиллярные эффекты, возникающие в результате взаимодействия наполнителей. Brutsaert [5] первым расширил теорию Био на случай трехфазной среды, однако исключив из рассмотрения капиллярные эффекты.
Общая система уравнений многофазной пористой среды была предложена Николаевским [6]. Работы Garg and Nayfeh [7], Santos и др. [8, 9], Tuncay и Corapcioglu [10, 11], Wei и Muraleetharan [12], Lo и др. [13], Lu и др. [14] по теории пористых сред с двумя жидкостями принадлежат концептуально к общему подходу, отличаясь в деталях реализации. Метод в целом состоял в разработке соотношений между напряжениями и деформациями для составляющих фаз с последующим использованием их в уравнении баланса в рамках стандартной механики сплошных сред. Berryman [15] вывел уравнения для частично насыщенных сред с использованием предположения о незначительном изменении капиллярного давления при прохождении через них акустического сигнала. Smeulders и др. [16] изучали распространение волн сжатия в пористой среде, заполненной жидкостью с небольшой объемной долей газа. В работах Thomas [17, 18] предложена конечно-элементная модель для анализа волновых полей напряжений, перемещений и порового давления в ненасыщенном морском дне. Мейснер и Беккер [19] установили влияние капиллярных эффектов на динамическое поведение частично насыщенного песка. Обзор доступных аналитических решений задач о распространении волн в насыщенных пористых средах можно найти в статье Schanz [20]. Однако для ненасыщенных моделей известно немного существующих аналитических решений. Можно отметить решение, полученное в работе Li и Schanz [21], для одномерного частично насыщенного пороупругого стержня. Поскольку получение аналитического решения часто возможно лишь в некоторых специальных случаях и при определенных видах граничных условий, решение задач динамики частично насыщенных пористых сред требует привлечения развитых численных методов, таких как МКЭ и МГЭ. В случаях бесконечных и полубеско-нечных тел и сред метод МГЭ является наиболее предпочтительным универсальным подходом к исследованию волн. Для рассмотрения задачи о распространении волны необходимы динамические формулировки исходной системы дифференциальных уравнений и соответствующие ей ГИУ, фундаментальные и сингулярные решения. В работах Gatmiri и Jabbari [22, 23] получены фундаментальные решения для статических и квазистатических задач теории ненасыщенных грунтов в двух- и трехмерной постановке. Соответствующие термо-упругие фундаментальные решения двух и трехмерных статических и квазистатических задач для частично насыщенных сред представлены в работах Jabbari и Gatmiri [24], Gatmiri и др. [25], Maghoul и др. [26]. Динамические формулировки ГИУ и фундаментальные решения для двухмерных задач представлены Maghoul и др. в [27], для трехмерных Ashayeri и др. в [28], Li в [29]. Авторами рассматривается трехкомпонентная пороупругая среда Био с пятью базовыми функциями описания волнового процесса – перемещениями скелета и поровым давлением жидкости и газа. ГИУ получены на основе метода взвешенных невязок, фундаментальные решения представлены в терминах преобразования Лапласа по переменной времени, при построении шаговой гранично-элементной схемы используется метод квадратур свёрток.
В настоящей работе представлена гранично-элементная методика на основе шагового метода численного обращения интегрального преобразования Лапласа для решения начально-краевых трехмерных задач динамики частично насыщенных пороупругих тел. Шаговый метод численного обращения преобразования Лапласа опирается на квадратурные формулы для интеграла, получаемого из теоремы операционного исчисления об интегрировании оригинала. Методика исследований основана на граничных интегральных уравнениях прямого подхода трехмерной пороупругости в преобразованиях по Лапласу, на компьютерном моделировании искомых решений методом граничных элементов в сочетании с методом коллокации, локальной поэлементной аппроксимацией на основе согласованной модели интерполирования Гольдштейна.
Математическая модель
Рассматривается частично насыщенный пористый материал, который представляет собой упругий скелет с порами, заполненными жидкостью и газом, при этом исключается испарение жидкости и растворение газа [29]. Кроме того, предполагается, что все три фазы являются сжимаемыми, имеют постоянную температуру, а любые изменения температуры не учитываются.
Для частично насыщенного пористого материала пористость обозначается как
V
__ void ф" V , где Void - объем взаимосвязанных пор в образце объема V . Закрытые поры рассматриваются как часть упругого скелета. Степень насыщения материала жидкостью Sw и газом Sa определяется как отношение занимаемого наполнителем объема Vw и Va соответственно к общему объему пор, т.е.
VV
S _ ——, Sa _ ——, Sa + S _ 1. (2)
w a aw void void
Существенным отличием частично насыщенных пористых сред от частично ненасыщенных является необходимость учитывать взаимодействие наполнителей. В результате искривления поверхности жидкости, вызванного действием сил поверхностного натяжения на границе раздела сред, возникает разность давлений в жидкости pw и газе pa , которая называется капиллярным давлением p c . Капиллярное давление может быть представлено как функция степени насыщения
- 1
pc _ P a - P w _ P d S e 8 . (3)
Величина pd определяет давление газа, необходимое для вытеснения жидкости из пор. Коэффициент 0 , характеризующий распределение размера зерен скелета, обычно принимает значения от 0,2 до 3. S e - эффективная водонасыщенность определяется следующим образом [29]:
0, w rw ra rw
1,
S w ^ S rw , S rw < S < S ra ,
Sw > Sra , где Srw - остаточная водонасыщенность; Sra - остаточная газонасыщенность.
Определяющие соотношения для суммарного напряжения вслед за [30] могут быть записаны в виде
Ч V - 5 S «( S . P” + S . P " ) . (5)
Здесь oj обозначено эффективное напряжение и а _ 1 - K / Ks - коэффициент эффективных напряжений, определяющий зависимость сжимаемости упругого скелета от его объ- емного модуля K и объемного модуля его зерен Ks. Скелет считается изотропным и однородным с двумя константами упругого материала: объемный модуль K и модуль сдвига G . Исходя из этих предположений получена формулировка для напряжения:
(„ 2
^ij И K - 3 G J 5ijuk’k + G ^ uiJ + uj,i ^
Кроме того, в допущении о малых градиентах деформации полагаем, что компоненты тензора деформаций твердого тела a j и смещения u i связаны соотношением
£ j =2 ( u,j + " ji i ) (7)
Уравнения баланса массы для твердого тела и наполнителей имеют вид
|
д [(1 -Ф ) р s ] д t |
div |
(1 |
д u - Ф ) р s ^T д t |
= 0. |
(8) |
|
|
д(ф S w р w > + div д t |
Ф S w |
р w |
д( u i + д t |
"Л 1 J |
w = р w1 , |
(9) |
|
д(Ф S ' р a ) + div д t |
Ф S a |
р a |
д( u i + д t |
"Л " |
a = р a1 , |
(10) |
w где рs, рw, рa - плотности твердотельного скелета, жидкости и газа соответственно, ui и и" - компоненты смещений наполнителей, относительных по отношению к скелету. Формулировка предполагает, что растворения газообразного наполнителя в жидкости не происходит, а градиенты плотностей, насыщенности и пористости пренебрежимо малы.
Для трехфазного материала можно записать
(^ G ) /Cw w с а\ г д 2 " д 2 u w д 2 u a
G " i, jj+\ K + v| uj , « -“ I ^ P , - + Sa P , - ) + Fi =P ^2“ + Ф S w P w + Ф S' P a , (11)
V 3 J д t д t д t e д uw
Ф S ■■ = д t
( w д2u д2uw]
'KwI P,- +Pw+PwЛ- I, V д t д t J
о дu
ФSa— = a д t
( a д2u д2ua
K a V P-+P a 1ё +P a IF
.
Уравнение (11) записано для скелета, уравнения (12), (13) - для жидкости и газа соответственно. Введена объемная сила F i и усредненная плотность р = (1 -ф ) р s +ф Sw р w +ф Sa р a . Перенос наполнителей определяется законом Дарси. Соответствующие фазовые проницаемости определяются как к w = K rw k / n w и к a = Krak I n a , где K rw и Kra - относительные фазовые проницаемости; k - внутренняя проницаемость материала; n w и П a - вязкости наполнителей. Относительная фазовая проницаемость определяется как отношение фазовой проницаемости к абсолютной. Используем вслед за [31] следующие экспериментально установленные зависимости для относительных про-ницаемостей в случае газоводяной смеси в порах:
K rw = S ^'6 , K ra = (1 - S e ) 2 [ 1 - S ^9] ■ (14)
Система уравнений (8)-(13) полностью описывает поведение частично насыщенного пороупругого континуума. Выберем в качестве базовых функций давление в порах p w , p a и перемещение скелета u i .
Для дальнейшего рассмотрения применяется интегральное преобразование Лапласа. Пусть f ( t ) - функция по t , f ( t ) = 0 для t < 0. Функция преобразования по Лапласу и ее обращение определено следующим образом:
f ( s ) = j f ( t ) e - st dt , s = a + i щ , (15)
1 a+ i ^
f ( t ) =--- f ( s ) e s ds (формула Римана-Меллина), (16)
2 n i a- i »
где s - комплексный параметр преобразования; a - вещественное число большее, чем вещественные части всех особенностей f (s). Применяя преобразование Лапласа к уравнениям (12), (13) и исключая относительные смещения uW и u., получаем i w
qi
i w
= SUi
в ( - w , 2 -
----( P i + Р w s U ФР w s
a aa Г ( a a 2 а qi = sui =--( pi + pas ui
ФР as ’
где q W , q “ - потоки наполнителей. В (17) введены следующие обозначения:
в= К W ФР w s , Y= К a ФР a s . (18)
Ф Sw +К w Р w s Ф Sa +К a Р a s
Подстановка (17) в уравнения (8)-(11) позволяет получить формулировку
GS , ., +( K + G 1 U„ - ( р-Р S w Р w -Y S a Р a ) s 2 U i - ( a-в ) S w p w - ( a-Y ) S . p " = - F , (19)
-(a-p) S w sul. i
Z S„A + -Ф- S w - S u ) sp w -в ' /' ■
I Kw ) Р w s
a. .
-(a-Y) S a su ii - (Z S ww S a + S u ) sp w
-
Z SflflSa +— S aaa a
V K a
-
S u I sp) a +^S^
Р a s
p a = - I a ,
где a__Ф С А С A V - ®(Sra Srw) I Sw Srw
Z 7^ , S ww S w y ( S w S rw ), S aa S a + ^V S w S rw ), S u dec
K p S_ - S_.,
Уравнения (19)-(21) могут быть записаны в операторной форме:
В =
а uw
А p
a
- Fi
-
- I a
с несамосопряженным оператором в =
A 1 5 , + A 2 8 , 8 , A d y A^ y
Ad
A 6
A 9
A 4 8 ,
A 7
A10
4 = G V 2 - ( p-р S , p , -Y S a p , ) s 2 , A 2. = K + 3, A , = - ( a-P ) S , , A 4 = - ( a-y ) S , ,
-
A , =- ( a-P ) S , s , A = -| Z S„S , + ^- S , -S , 1 s + ^ V 2 , A 7 =- ( ; S„S , + S , ) s , I K , ) p ,s
-
2. Граничные интегральные уравнения и фундаментальные решения
A =- ( a-Y ) S , s , A = - ( Z S„S , + S , ) s , Aw =-US ,, S , +-^- S , - S , 1 s + ^ S a V 2 .
I K, ) p as
Применение интегрального преобразования позволяет строить метод граничных интегральных уравнений.
Фундаментальное решение находится из следующего операторного соотношения:
E UJ + I 5 ( x - y ) = 0 , (23)
где I - единичная матрица; 5 - дельта-функция Дирака; x , y e R 3 .
Итоговая матрица фундаментальных решений
Гранично-интегральное уравнение для динамической пороупругости в области Лапласа можно получить на основе традиционных формулировок: теоремы взаимности или метода взвешенных невязок. Пороупругий оператор является несамосопряженным, а значит, для этих методов требуются разные фундаментальные решения, но в конечном счете оба метода дают одно и то же интегральное уравнение.
Интегральное уравнение динамической пороупругости, построенное на основе метода взвешенных невязок, имеет вид
I
г
ˆ ss Uij
U i ws U ˆ i as
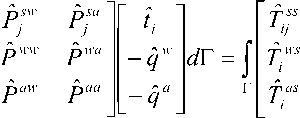
|
Qs j w |
Q 7 |
A u |
" с у |
0 |
0" |
A u , |
|
|
Q ˆ ww |
Q - |
A , p |
d r + |
0 |
c |
0 |
p w |
|
Q ˆ aw |
Q aa |
p a |
0 |
0 |
c |
p a |
где
ss ij т ws
Ti г as
Ti
Qs j w Q ww Q a w
Qs j a
Qwa
Qaa
- матрица сингулярных решений; t i = 5 i n - поверхностная сила;
qw =( p™ + pws2Ui) n - поток жидкости; qa =——(pa + pas2Ui) ni - поток газа; n -pws , pas , вектор внешней нормали. Построенные граничные интегральные уравнения являются сингулярными и существуют в смысле Коши. Для нахождения решения граничных интегральных уравнений требуется соответствующая методика их дискретного представления. В работе используется гранично-элементный подход.
-
3. Гранично-элементная (ГЭ) дискретизация
Чтобы ввести ГЭ-дискретизацию, рассмотрим регуляризованное уравнение [32]:
anu k ( x, s ) + J ( Тй ( x , y , s ) ц ( y , s ) - T ( x , y , s ) ц ( x , s ) - Uy. ( x , y , s ) t ( y , s ) ) dS = 0,
S
(x e S), t = [t„ t2,13, qw, qa ]T, u = ( ц, u 2, U3, pw, pa), где Uik, Tik - матрицы фундаментальных и сингулярных решений; Tik - матрица компонент, содержащих особенности; t - вектор обобщенных усилий; и - вектор обобщенных перемещений.
Базовый процесс ГЭ-дискретизации состоит в разбиении поверхности на NЕ граничных элементов E e (1 < e < NЕ ) совокупностью четырехугольных и треугольных восьмиузловых биквадратичных элементов. При этом треугольные элементы рассматриваются как вырожденные четырехугольные элементы, каждый из которых отображается на контрольный элемент A e (каждый A e - это либо квадрат £ = ( ^ 1 , ^ 2) e [ - 1,1 ] 2, либо треугольник 0 <^ +^ 2 < 1, ^ 1 > 0, 4 . > 0).
Неизвестные граничные поля ( и , t ) определяются через узловые значения и k = u ( z k ) и t k = t ( z k ) в интерполяционных узлах. При этом для расчетного значения параметра s будем иметь следующие выражения граничных перемещений и поверхностных сил внутри элемента S k :
и , ( y ) = ^ R ©и «‘ ■ ' ) , i = 1,2,3; y e S , , l = 1
t i ( y ) = f t ( k , 1 ) , i = 1,2,3; y e S k .
Здесь R l ( ^ ) - функции формы для линейного четырехугольного элемента.
Для получения дискретного аналога ГИУ применим метод коллокации. В качестве узлов коллокации будем выбирать узлы аппроксимации исходных граничных функций. В итоге формируется система линейных алгебраических уравнений
1 a n
N 4
U m + ££ A m , k , l u j k , l ) k = 1 l = 1
= Z B m , k t k ,
k = 1
NL
1 " и m + ^^ A m’* ’ l u j(* ’ l ) = £ B m’k t k . 8 k = 1 l = 1 k = 1
Уравнения записаны соответственно в узлах аппроксимации обобщенных граничных перемещений и обобщенных поверхностных сил.
i 1
A j = f f [ R l©T, (x m ,/@. р ) "« x . *.i >Л ( x m . y* ( ^ >) ] J ( 9 d - 1 d 9 .
-
- 1 - 1
-
1 1
j = f f U , ( x m . y * ( - ). р ) J * ( 9 ) d - d - 2 .
-
- 1 - 1
-
4. Шаговая схема численного обращения преобразования Лапласа
Рассмотрим метод, опирающийся на теорему об интегрировании оригинала, - шаговый метод численного обращения преобразования Лапласа.
Рассмотрим следующий интеграл:
t
У ( t ) = f f (т) d т .
Интеграл (26) порождает задачу Коши для обыкновенного дифференциального уравнения
— x ( t ) = sx ( t ) + C . x (0) = 0. dt
Интеграл (26) заменяется квадратурной суммой. весовые множители которой определяются с помощью изображения по Лапласу f и линейного многошагового метода [33-36]. Дальнейшее изложение идет с учетом результатов этих работ. Традиционный шаговый метод интегрирования оригинала состоит в том. что интеграл (26) считается по следующему соотношению:
n
У (0) = 0. у ( n A t ) = ^ ю * ( A t ). n = 1.... N .
k = 1
где to „ (A t )
R-n 2r ' ( y(Rei9)л 2nf f I At J e-m 9 d ф.
Единственная аппроксимация. которая используется при выводе формулы (27). заключается в применении линейного многошагового метода для решения задачи Коши дифференциального уравнения первого порядка. Все остальные вычисления проводятся непосредственно. Многошаговый метод должен быть порядка точности p > 1 . являясь строго ноль-устойчивым или A -устойчивым. а функция f ( s ) ограничена в правой полуплоскости относительно прямой ( c - i го . c + i го ) . то есть
_ f ( s ) < 4 s |"'
при K < го . ц > 0.
Если функция fˆ(s) аналитична и ограничена в области | arg( 5 - c )| <п-ф, где ф < -2
критерий устойчивости может быть ослаблен до A ( а )-устойчивости.
Выражаясь в терминах характеристической функции у ( z ) :
-
• функция у ( z ) не должна содержать нулей и полюсов внутри замкнутого единичного круга (| z | < 1 ) за исключением однократного нуля при | z | = 1;
-
• |arg у ( z )| <п-а , где | z | < 1 при а > ф;
-
• A t 1 у ( e A t ) = 1 + O ( A tp ), где A t ^ 0 при p > 1.
К соответствующим примерам многошаговых методов относятся методы дифференцирования назад порядка p < 6: для A-устойчивого метода дифференцирования назад второго порядка (а = 90о) можем записать следующую характеристическую функцию:
Y ( z ) = 3/2 - 2 z + z 2/ 2.
Следующая аппроксимация, которая используется в методе, – численное интегрирование, при получении значений ю n ( A t ) аппроксимируем с L равными шагами 2 л/ L :
- n L — 1
R
ю n(A t)=тЕ f
L l = 0
/ il 2 п \
Y ( Re L )
A t
e
inl L
При условии, что функция f ˆ( s ) в уравнении (28) вычисляется с некоторой погрешностью s выбор L = N и R n = Vs допускает погрешность вычисления ю n порядка О (Vs) .
-
5. Численные эксперименты
Рассматривается задача о действии торцевой силы на призматическое пороупругое тело длиной 3 м, высотой и шириной 1 м, с жестко закрепленным концом. Краевая задача представлена на рис. 1. Отклики перемещения uz и поверхностные усилия tz , вызванные силой F ( t ) = 1 Н/м2, наблюдаются соответственно на нагруженном и на закрепленном торцах. Параметры частично насыщенного пористого материала соответствуют параметрам песчаника: K = 1,02 - 10 9 Н/м2, G = 1,44 - 10 9 Н/м2, ф = 0,23 , р 5 = 2650кг/м3 , р = 997 кг/м3 , р = 1,10 кг/м3, K = 3,55 - 1010Н/м2, K = 2,25 - 10 9 Н/м2, wa s w
K a =1,10 - 10 5 Н/м2, к =2,5 - 10 - 12 м2, n w = 1,0 - 10 - 3 Нс/м2, n a = 1,8 - 10 - 5Нс/м2, S w = 0,9, S rw = 0, S ra = 1, 6 = 1,5. На временном интервале от 0 с до 0,035 с шаг по времени A t выбирается из условия L = N , параметр R принят равным 0,997. Задача решается в трёхмерной постановке. Заданные граничные условия позволяют сравнивать решение исходной задачи с решением соответствующей одномерной задачи, представленным в [21].
При решении использовались три гранично-элементные сетки с различной степенью пространственной дискретизации (рис. 2). Наличие двух плоскостей симметрии дает возможность рассматривать только часть сетки, при этом четверть сетки a содержит 14 элементов, сетки б – 56 элементов, сетки в – 126 элементов.
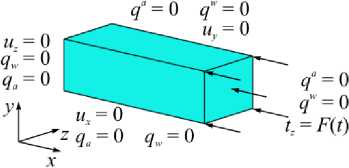
Рис. 1. Геометрическая модель и граничные условия задачи о частично насыщенной пороупругой консоли
Fig. 1. Geometry and boundary conditions of a partially saturated poroelastic column

а б в
Рис. 2. Гранично-элементные сетки: a – 56 элементов; б – 224 элемента; в – 504 элемента
Fig. 2. Boundary-element meshes: a – 56 elements; b – 224 elements; c – 504 elements
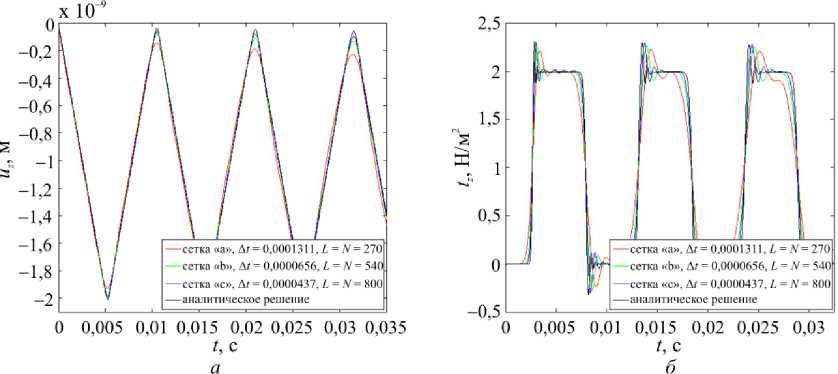
Рис. 3. Гранично-элементные решения, полученные на трех различных сетках: a – перемещения; б – усилия
Fig. 3. Boundary-element solutions on the three different meshes for: a – displacements; b – tractions
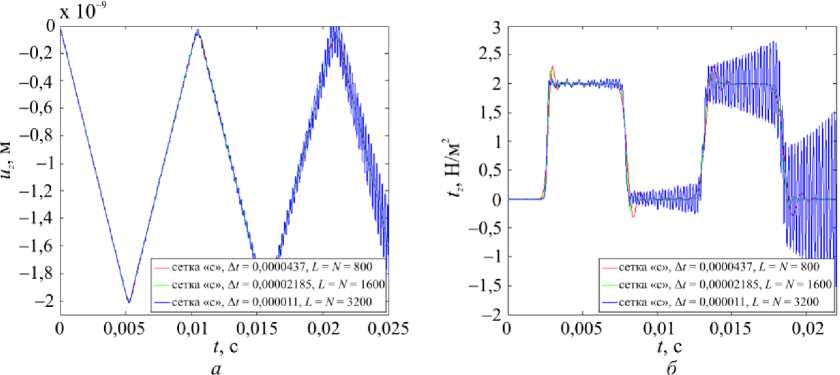
Рис. 4. Гранично-элементные решения, полученные при трех различных значениях параметра шагового метода: a – перемещения; б – усилия Fig. 4. Boundary-element solutions for the three different values of the time-step method parameter for: a – displacements; b – tractions
Результаты исследования сходимости по расчетной сетке показывают, что с ростом числа элементов гранично-элементные решения для перемещения (рис. 3, а ) и напряжения (рис. 3, б ) принимают значения, близкие к рассчитанным по аналитическим формулам. Варьирование параметром шаговой схемы Δ t приводит к тому, что при снижении его до значения 0,00002185 c в расчетах на сетке c наблюдается незначительное уточнение амплитуды решения (рис. 4, а , б ), однако при дальнейшем его уменьшении решение расходится.
Заключение
Дано описание математической модели частично насыщенной пористой среды, основанной на модели Био, с пятью базовыми функциями. В изображениях по Лапласу приведена математическая модель краевой задачи трехмерной динамической теории пороупру-гости. Представлен шаговый метод численного обращения преобразования Лапласа. Дано описание методики гранично-элементного моделирования. Решена задача о действии нагрузки на торец призматического частично насыщенного пороупругого тела. Полученные гранично-элементные и рассчитанные аналитически значения искомых величин графически неразличимы.
Работа выполнена при финансовой поддержке Российского научного фонда (проект № 15-19-10056).
Список литературы Моделирование динамики частично насыщенных пороупругих тел на основе метода гранично-временных элементов
- Frenkel J. On the theory of seismic and seismoelectric phenomena in a moist soil//Journal of Physics. -1944. -Vol. 8. -P. 230-241.
- Косачевский Л.Я. О распространении упругих волн в двухкомпонентных средах//Прикладная математика и механика. -1959. -Т. 23, № 6. -С. 1115-1123.
- Biot M.A. Theory of propagation of elastic waves in a fluid-saturatedporous solid. I. Low-frequency range//Journal of the Acoustical Society of America. -1956. -Vol. 28. -P. 168-178 DOI: 10.1121/1.1908239
- Biot M.A. Theory of propagation of elastic waves in a fluid-saturated porous solid. II. Higher-frequency range//Journal of the Acoustical Society of America. -1956. -Vol. 28. -P. 179-191 DOI: 10.1121/1.1908241
- Brutsaert W. The propagation of elastic waves in unconsolidated unsaturated granular mediums//Journal of Geophysical Research. -1964. -Vol. 69. -P. 243-257 DOI: 10.1029/JZ069i002p00243
- Nikolaevskij V.N. Mechanics of porous and fractured media. Singapore, World Scientific, 1990. -472 p.
- Garg S.K., Nayfeh A.H. Compressional wave propagation in liquid and/or gas saturated elastic porous media//Journal of Applied Physics. -1986. -Vol. 60. -P. 3045-3055 DOI: 10.1063/1.337760
- Santos J.E., Corberó J.M., Douglas J.Jr. Static and dynamic behavior of a porous solid saturated by a two-phase fluid//Journal of the Acoustical Society of America. -1990. -Vol. 87. -P. 1428-1438 DOI: 10.1121/1.399439
- A model for wave propagation in a porous medium saturated by a two-phase fluid/J.E. Santos, J.Jr. Douglas, J. Corberó, O.A. Lovera//Journal of the Acoustical Society of America. -1990. -Vol. 87. -P. 1439-1448 DOI: 10.1121/1.399440
- Tuncay K., Corapcioglu M.Y. Body waves in poroelastic media saturated by two immiscible fluids//Journal of Geophysical Research. -1996. -Vol. 101. -P. 25149-25159 DOI: 10.1029/96JB02297
- Tuncay K., Corapcioglu M.Y. Wave propagation in poroelastic media saturated by two fluids//Journal of Applied Mechanics. -1997. -Vol. 64. -P. 313-320 DOI: 10.1115/1.2787309
- Wei C., Muraleetharan K.K. A continuum theory of porous media saturated by multiple immiscible fluids: I. Linear poroelasticity//International Journal of Engineering Science. -2002. -Vol. 40. -P. 1807-1833 DOI: 10.1016/S0020-7225(02)00068-X
- Lo W.-C., Sposito G., Majer E. Wave propagation through elastic porous media containing two immiscible fluids//Water Resources Research. -2005. -Vol. 41. -P. 140-160 DOI: 10.1029/2004WR003162
- Lu J.-F., Hanyga A., Jeng D.-S. A mixture-theory-based dynamic model for a porous medium saturated by two immiscible fluids//Journal of Applied Geophysics. -2007. -Vol. 62. -P. 89-106 DOI: 10.1016/j.jappgeo.2006.08.002
- Berryman J.G. Waves in partially saturated porous media/Eds. In W.E. Fitzgibbon, M.F. Wheeler//Wave Propagation and Inversion (Proceedings of SIAM Conference on Mathematical and Computational Issues in Geophysical Fluid and Solid Mechanics) SIAM, Philadelphia, 1992. -P. 1-25.
- Smeulders D., De La Rosette J., Van Dongen M. Waves in partially saturated porous media//Transp. Porous. Med. -1992. -Vol. 9. -P. 25-37.
- Thomas S.D. A finite element model for the analysis of wave induced stresses, displacements and pore pressures in an unsaturated seabed I//Theory. Comput. Geotech. -1989. -Vol. 8. -P. 1-38.
- Thomas S.D. A finite element model for the analysis of wave induced stresses, displacements and pore pressures in an unsaturated seabed II//Model verification. Comput. Geotech. -1995. -Vol. 17. -P. 107-132.
- Meissner H., Becker A. Dynamic behaviour of partially saturated sand//T. Built Environ. -1995. -Vol. 14. -P. 45-55.
- Schanz M. Poroelastodynamics: Linear models, analytical solutions, and numerical methods//Appl. Mech. Re. -2009. -Vol. 62 (3). -15 p.
- Li P., Schanz M. Wave propagation in a 1-d partially saturated poroelastic column//Geophys. J. Int. -2011. -Vol. 184. -P. 1341-1353.
- Gatmiri B., Jabbari E. Time-domain green’s function for unsaturated soils. Part I: two-dimensional solution//International Journal of Solids and Structures. -2005. -Vol. 42. -P. 5971-5990.
- Gatmiri B., Jabbari E. Time-domain Green’s function for unsaturated soils. Part II: three-dimensional solution//International Journal of Solids and Structures. -2005. -Vol. 42. -P. 5991-6002.
- Jabbari E., Gatmiri B. Thermo-Poro-Elastostatic Green Functions for Unsaturated Soils//Comput. Model. Eng. Sci. -2008. -Vol. 18 (1). -P. 31-43.
- Gatmiri B., Maghoul P., Duhamel, D. Two-dimensional transient thermo-hydro-mechanical fundamental solutions of multiphase porous media in frequency and time domains//Int. J. Sol. Struct. -2010. -Vol. 47. -P. 595-610 DOI: 10.1016/j.ijsolstr.2009.10.022
- Maghoul P., Gatmiri B., Duhamel D. Three-dimensional transient thermo-hydro-mechanical of unsaturated soils//Int. J. Numer. Anal. Methods Geomech. -2009. -Vol. 34. -P. 297-329 DOI: 10.1002/nag.820
- Maghoul P., Gatmiri B., Duhamel D. Boundary integral formulation and two-dimensional fundamental solutions for dynamic behaviour analysis of unsaturated soils//International Journal of Soil Dynamics and Earthquake Engineering. -2011. -Vol. 31 (11). -P. 1480-1495.
- Analytical 3d transient elastodynamic fundamental solution of unsaturated soils/I. Ashayeri, M. Kamalian, M.K. Jafari, B. Gatmiri//Int. J. Numer. Anal. Methods Geomech. -2010. -Vol. 35. -P. 1801-1829.
- Li P. Boundary element method for wave propagation in partially saturated poroelastic continua. Computation in engineering and science. Graz: Verlag der Technischen Universität, 2012.
- Bishop A.W., Blight G.E. Some aspects of effective stress in saturated and partly saturated soils//Geotechnique. -1963. -Vol. 13. -P. 177-197.
- Brooks R.H., Corey A.T. Hydraulic properties of porous media. -In Hydraulic Papers. Colorado State Univ., 1964.
- Баженов В.Г., Игумнов Л.А. Методы граничных интегральных уравнений и граничных элементов в решении задач трехмерной динамической теории упругости с сопряженными полями. -М.: Физматлит, 2008. -352 с.
- Lubich C. Convolution quadrature and discretized operational calculus//Numer. Math. I. -1988. -Vol. 52 (2). -P. 129-145.
- Lubich C. Convolution quadrature and discretized operational calculus//Numer. Math. II. -1988. -Vol. 52 (4). -P. 413-425.
- Schanz M. Wave Propagation in Viscoelastic and Poroelastic Continua. -Berlin Springer, 2001. -170 p.
- Литвинчук С.Ю., Петров А.Н., Сабаева Т.А., Решение задачи о действии давления внутри полости в пороупругом полупространстве//Проблемы прочности и пластичности. -2014. -№ 76 (2). -C. 97-105.


