Моделирование динамики численности населения при социально-экономических ограничениях

Демографические и социально-экономические процессы в обществе, как правило, взаимосвязаны. В данной работе, используя идеи работы [1], проводится моделирование численности населения в зависимости от уровня социально-экономического развития региона и способа распределения дохода (заработной платы) между различными группами активного и неактивного населения. Такая проблема не только очень актуальна, но и сложна для исследования и идентификации, недостаточно изучена.

Модель строится при следующих социально-экономических гипотезах:

• 1)    основные региональные процессы идеализированы, в частности, регион рассматривается как замкнутая система, миграционными процессами пренебрегаем на данном этапе формализации и рассматриваем краткосрочный прогноз для самостоятельного региона;

• 2)    при высокой доле молодежи в составе населения в населении будет наблюдаться высокий уровень вступающих в брак в репродуктивном возрасте, высокая рождаемость и низкий уровень смертности; обратно, снижение рождаемости приводит к демографическому старению населения и этот процесс инерционный, с запаздыванием [2];

• 3)    выбор групп населения и условия распределения доходов в различных группах соответствуют российским социально-экономическим реалиям и могут быть представлены несложными (например, дифференциальными, интегральными, разностными полуэмпирическими) соотношениями;

• 4)    возрастная структура описывается с помощью относительных обобщенных показателей, которые должны указывать лишь качественное направление развития процесса.

Рассмотрим общую концепцию модели. Все население региона разбиваем на 4 группы: дети, трудоспособные работающие, трудоспособные безработные, пенсионеры. Ежегодно численность населения фиксируется в определенный момент времени, например, на первое января каждого года. Производство – однопродуктовое. Время дискретно: t = 1, 2, …, T, шаг – 1 год. Динамику численности населения опишем рекуррентным матричным уравнением:

xt+1 = M ( zt) xt , ^ b1( z1) + s 1( z1) b2( z 2)   ■•• bn-1( zn-1) bn (zn ) s 1( z1) s 2( z 2)   ■•• 0 0 M ( z ) = 0 s 2( z 2)   ... 0 0 к      0 0      ... sn-1( zn-1) sn(zn) где b. (z) - коэффициент рождаемости; s. (z. ) = Si (z.) + s. (z) - коэффициент выживаемости; si e [0,1] — относительная доля перешедших из группы i в группу i +1 (доживших до такого перехода); s e[0,1] -относительная доля остающихся в группе i.

Матрица M(z) может быть выбрана как матрица переходных вероятностей соответствующим образом определенного марковского процесса.

Пусть q = ( q , q₂ ,..., q_n ) - вектор квалификации людей, то есть вектор усредненных, например, по группам профессиональной квалификации людей. Тогда будем считать количество трудовых ресурсов пропорциональным численности населения с учетом внутригрупповой квалификации:

• ^lt = q 1 x 1 ⁺ q 2 x 2 ^{+    +} q n x n .

Заработную плату w ^t считаем пропорциональным квалификации:

wt = at q, где at > 0 - квалификационные параметры.

Динамику производственного капитала опишем следующим соотношением:

k+i = kt (1- a)+(pyt - a (qixi +-+qnxn)), где ^ - норма выбытия капитала, p - цена единицы продукции

(услуги).

В качестве функции цели выбираем функцию, выражающую общую численность населения для следующего момента времени [3]:

n c (z ) = X xts (zi).

i = 1

На базе производственной функции типа Кобба-Дугласа:

y = y 0

l t

—

l

^e (1—lt

.   l — 1 0/?

Y м " (

kt

—

k

k - k о

^{л e} 2 ( k — k_t X^k о ^{— k}

■ в

к ¹ о    ¹ J

к

l — 1 0 J

к ^k 0 ^— k J

к

^{k — k} о J

,

где у – проектное значение показателя, у0 – начальное значение показателя, l – управляющий фактор, от которого зависит у, l – верхняя граница l, l – нижняя граница l, l – оптимальное значение l, k – управляющий фактор, от которого зависит у, k – верхняя граница k, k – нижняя граница к, k0 - оптимальное значение к, в, в — параметры, характеризующие темпы роста у с увеличением l и к, в + в = 1, получаем модель типа производственной функции:

y = у 0 L * ^ 1 ( l ) K * - ^{в 1} („к ),

L * ( l ) =

*

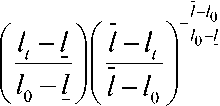
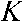
( k_t - к V к — k_t^Л

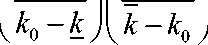
к — k ₀

— k0 — k

Используя видоизменённый функционал адекватности метода наименьших квадратов [4]: n

F = £(ln | у01 + в ln | L.i (l) | +(1 — Д)ln | K* (k) | — In | y’ |)2----->min, i=1

L = L (l_t ), K = K ( k _?) , * i *                  * i *

и достаточное условие экстремума получаем условие вида:

£ ( 2ln K ( ln| y_г^э | + In L — ln| y ₀1 — In K ) + 2ln L* ( ln| y ₀1 — ln| y Э |) —

— в ( 4ln K ln L + 2ln² K

+ 2ln²

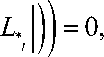
1iii из последнего соотношения находим идентифицируемый параметр:

в =

t ( ln K *

i =1 \              i

+ ln

LY

+ ln L*

i

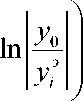
в 2 = 1 — в 1 .

Учитывая эти значения идентифицированных параметров, определяем проектное значение y.

Разработана программа имитационного моделирования в среде Borland C++ Builder, которая демонстрирует зависимость численности населения от экономических факторов, таких как объем производства, производственный капитал, доход на душу населения. По начальным данным о численности населения по группам, количестве работающих, производственном капитале, "Экономика и социум" №1(10) 2014 душевом доходе и объеме производства программа выполняет расчет прогнозируемых показателей. Также программа позволяет производить имитационное моделирование показателя роста в функции Кобба-Дугласа. По статистическим данным за несколько предшествующих лет производится расчет показателя роста в предположении его стабильности в течение нескольких лет.