Моделирование динамики дозаторных систем с гидравлическим приводом

В качестве примера рассматриваются дозаторные системы с гидравлическим приводом на основе центробежных и шестеренчатых насосов, структурно-функциональная схема которых представлена на рис. 1.

В процессе моделирования динамики дозатора приняты следующие гипотезы: жидкость сжимаема, стенки цилиндров 2 и 5 податливы, поршни цилиндров 2 и 5 – жесткое целое. Унифицированная расчетная схема, позволяющая вести расчеты для центробежного (связь I ) или для шестеренчатого (связь II ) насоса на основе схемы рис. 1, приведена на рис. 2.

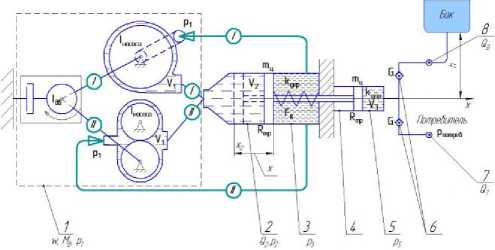
Рис. 2. Расчетная схема насоса-дозатора с гидравлическим приводом:

Q ₂ =S ₂ v_п , Q ₇, Q ₈ – расход жидкости в соответствующих элементах, м³/с; p 1 , p 2 , p 3 , p 5 , p 7 , p 8 – давление в соответствующих элементах, Мпа; x – перемещение поршня, м; v п = x – скорость поршня, м/с; ω – угловая скорость ротора двигателя, рад/с; M _д – момент электродвигателя, Н·м; V 1 – рабочий объем насоса, м³

Математические соотношения, описывающие работу дозатора в соответствии с расчетной схемой рис. 2, при учете динамической взаимосвязи всех его элементов [2-6], представлены системой уравнений:

^ 1 [ M g U ( t ) i - V н ( Р 2 - Р 1 ) ]

_ (А V 2 + x5 2 ) f    d 2 E Ж2 )

A_vn =                 I 1 +I

• ^УПр²       E ж2     I   8 2 E„2 j

dP 2 = V.^H  5 2 Vп dt      Kупр2

P g = P 2 ⁵ 2 ^- P 3 ⁵ 3 ^- P 5 ⁵ 5 ^- c ц ^{( X} 0 ^{+ X} )

n  _ n 0   , ™P 2 ^d 2 ^H 2 „ I ,

R тр = R тр ⁺---2--- ^P 2 ⁺

+ ( H 2 + H 5 ) V n|

тар ₂( d ₂ + d ‘ ) H

1 p ,1- ’^{ф (} d 5 + d ⁵¹ H |P 5I ■ "^ф'^Ф " ' | p ,| +

dvn    "

¹¹ = 1 m,

¹ dt

1 Г             ■    /             Г

---^[ P g - R mp ^Sign⁽ v п ^{) ]}    1 m ц                     |

■ Vп = 0

. V п * 0

и

P g >  R тр

0,

V п = 0

и

Р д      тр

dx dt ~ vп

K

• упр5

_ (А V 5 + ( L - х ) 5 5 )

dp ₅ dt

⁵ 5 ^V п -

E ж5

'^Q 7 ^{+ Q} 8

d E d5Eж5

8 5 E „5

Q 7 =

Q 8 =

^K упр5 '0.

. G 7 V р 5 ^- р 7 . 0,

. G 8 V P 8 ^- P 5 .

Р 7 ^ Р 5

Р 7 <  Р 5

Р 5 ^ Р - 8

Р 5 <  Р 8 .

где I =( I _дв- I _ред1) i + I _ред2+ I _насос

– приведенный момент инерции двигателя, редуктора и насоса, кг·м ²; i – передаточное

число редуктора; U ( t ) – функция управления (1 – включено, 0 - выключено); S ₂, S ₃, S ₄, S ₅, d ₂, d ₅, d ₂' d ₅', δ₂, δ₅ – площади, м², диаметры и толщины стенок цилиндров, м; V н – активный объем насоса (центробежного V н = V 1 /2π, шестеренчатого V _н= bm ( z ₁+1)), м³; η – КПД насоса; Δ V ₂, Δ V ₅ – мертвые объемы полостей 2 и 5, м³; L – длина хода поршня, м; E ж2 , E ж5 , E ст2 , E ст5 , K упр2 , K упр5 , – модули упругости, МПа и коэффициенты упругости жидкости и стенок полостей 2 и 5; m _ц – масса поршня, кг; P _д – движущая сила поршня, Н; R _тр⁰, R _тр, φ₂, φ₅ – силы трения, Н, и коэффициенты трения в манжетах; c ц – жесткость пружины, Н/м; H 2 , H 5 – высота манжетного уплотнения в цилиндрах 2 и 5, м; G 7 , G 8 – проводимость клапанов 7 и 8 [5], м⁴·с^-1·Н^-0,5.

Для удобства моделирования система (1) с помощью идентификаторов переменных характери-

стик нормируется и приводится к виду:

dy i = ¹ [ M д yU ( t ) i - V . ( У 2 - P 1 ) ] dt I

( А V 2 + У 5 5 2 ) L

d 2 E ж2 ^ 8 2 E ст2 j

dy 2 _ Vн У1П- 5 2 У 4 dty

У 6 = У 2 ⁵ 2 ^- P 3 ⁵ 3 ^- У 3 ⁵ 5 ^- c ц ⁽ X 0 + У 5 )

„ _ D 0   . ”Ф 2 d 2 H 2 L, , ™P 2 ⁽ d 2 ⁺ d 2 ) H 2 _n , ™Ф 5 ⁽ d 5 ⁺ d 5 ) H 5 _n , ™Ф 5 d 5 H 5 L, I ,

У 7 = R тр +----2----У 21+--------2--------3'+-------2--------5 +----2

+ ⁽ H 2 + H 5)| ^У 4

Г у 4 = ⁰ и у 6 >  у 1

| ^У 4 * ⁰

У 4 = ⁰ и У 6 ^ У 7

оУ д    — [ У 6 ^- У 7 ^sign⁽ У 4 )1

= m„ dt

| 0.

dyy = У dt 4

_ (А V 5 + ( L - У 5 ) 5 5 ) Г, d d 5 E _ж5 )

• ^{У 11} =        Е         I 1 +ЪЕ I

Eж5        V   85Eст5 j dy 3 _ 55 У 4 - У 8+У 9

dt         y ₁₁

_ Г^0,                 Р 7 ^ У 3

• ⁸    [ G 7 V У 3 ^- Р 7 . Р 7 <  У 3

' 0.                У 3 ^ Р 8

• У 9 =1    /-------

• |G8у1 Р8 - У3. У3 < Р8

где ω=y1; p2=y2; p5=y3; vп=y4; x=y5; Pд=y6; Rтр=y7; Q7=y8; Q8=y9; Kупр2=y10; Kупр5=y11.

Системы (1-2) являются нелинейными и содержат как дифференциальные, так и алгебраические уравнения. Следует отметить переменное строение математических соотношений, так как в процессе нагнетания и всасывания изменяется ряд параметров и структура исходной системы. Математическое моделирование динамики дозатора осуществляется с помощью программного комплекса, в основе которого лежит метод Рунге-Кутта 4 и 5 порядков с автоматическим выбором шага (схема Dormand and Prince) в системе Matlab [7]. Процесс моделирования начинается с решения уравнения моментов на валу насоса, определяющего изменение его угловой скорости, в результате чего вычисляется расход насоса. Из уравнения сжимаемости жидкости определяется давление жидкости в нагнетательной камере гидроцилиндра, действующее на поршень, и приводящее его в движение при учете сил сопротивления. Вследствие разницы расхода, происходит приращение давления в камере дозатора. Функционирование клапана определяется возникающим перепадом давления в камере дозатора. Расход через нагнетательный клапан определяет расход всей системы дозатора. При перемещении поршня на длину рабочего хода, происходит отключение электродвигателя. Структура уравнений изменяется, осуществляется переход между рабочим и обратным ходами и фиксируется время tраб. Окончание процесса дозирования определяется временем рабочего и обратного хода tпол. Результаты процесса моделирования формируются в виде таблиц и графиков динамических характеристик процесса дозирования. На рис. 3-9 в качестве примера представлены фрагменты расчетов дозаторов с центробежным и шестеренным насосами, при давлении в магистрали потребителя 400 атм. и перемещении поршня 60 мм.

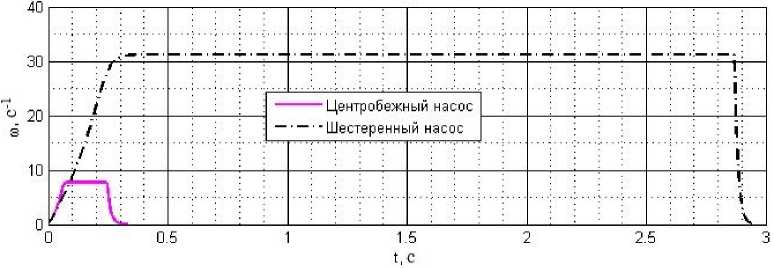
Рис. 3. График угловой скорости ротора двигателя

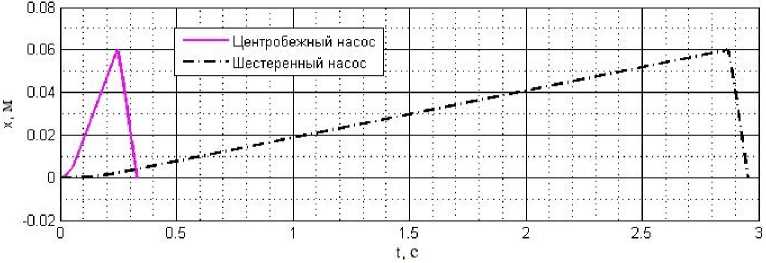
Рис. 4. График перемещения поршня

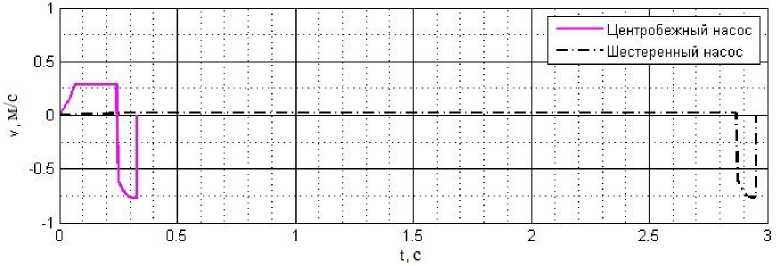
Рис. 5. График скорости поршня

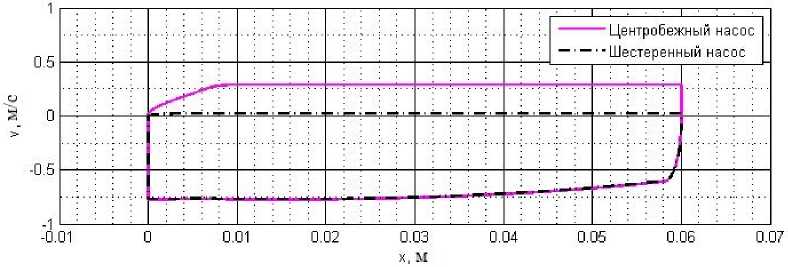
Рис. 6. Совмещенный график скорости и перемещения поршня

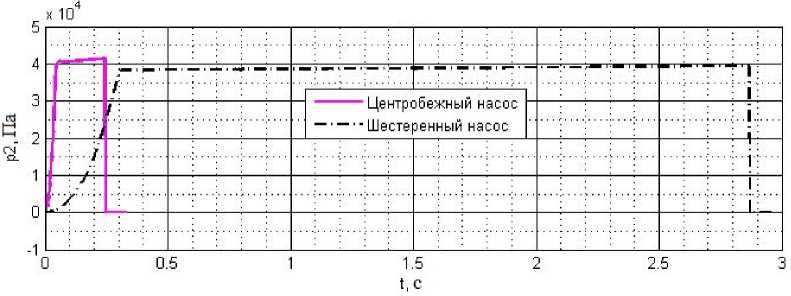
Рис. 7. График давления масла в напорном гидроцилиндре

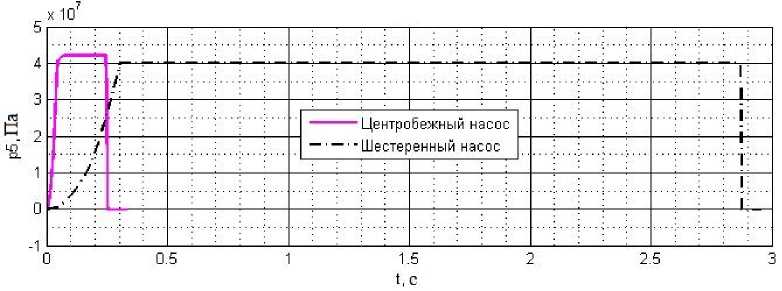
Рис. 8. График давления дозируемой жидкости в камере дозатора

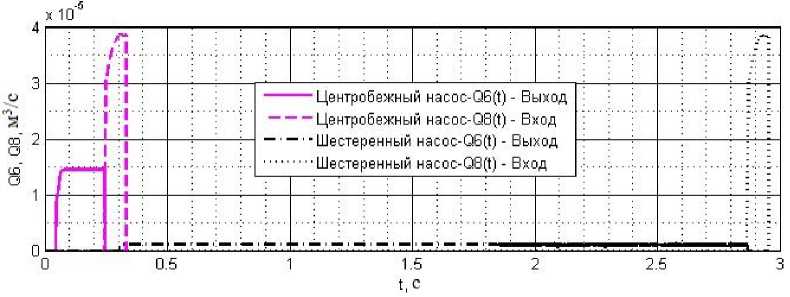
Рис. 9. График расхода дозатора

Выводы: проведенные расчеты показали значительное отличие рассматриваемых типов привода, как по конструктивно-технологическим параметрам, так и по и физическим характеристикам, необходимых для удовлетворения заданных параметров технологического процесса дозирования. Полученные результаты позволяют осуществить имитационное моделирование динамики дозаторных систем, численно оценить критерии качества функционирования и перейти к их оптимальному проектированию.