Моделирование динамики фильтрации двухчастичной суспензии через пористую среду

При движении суспензии через пористую среду имеет место удержание частиц в поровом пространстве и, как следствие, уменьшение пористости и проницаемости среды. Интенсивность накопления частиц в поровом пространстве зависит от многих параметров, например, скорости фильтрации, соотношения размеров частиц и поровых сужений (поровых «горлышек»). Если характерный размер частиц больше характерного размера поровых «горлышек», то частицы не проникают внутрь, а оседают на поверхности пористой среды, образуя внешнюю фильтрационную корку с низкой проницаемостью. Если характерный размер частиц меньше характерного размера поровых сужений, то имеет место проникновение частиц внутрь пористой среды, что сопровождается удержанием части частиц в поровом пространстве. Существуют различные механизмы удержания частиц пористой средой, например осаждение на стенки пор под действием силы тяжести или вследствие столкновения со стенками при движении по извилистым каналам, захват частиц поровыми сужениями, закупоривание поровых сужений несколькими частицами (сводовая кольматация).

Существует феноменологический подход к описанию процессов, происходящих в пористых средах. При таком подходе выделяются несколько макропараметров, с помощью которых описывают свойства пористой среды в целом. Данный подход позволяет воспроизвести усреднённые макроскопические величины, характеризующие пористую среду. В работах [1, 2] построена модель, описывающая движение суспензии неразличимых твердых частиц через пористую среду. В дальнейшем авторы работы [3] расширили модель введением механизма мобилизации частиц, ответственного за возвращение частиц в поток. Многие экспериментальные данные (см., например, [1, 2, 4, 5]) хорошо описываются в рамках модели [1, 2]. Однако существует ряд экспериментальных данных, например работа [6], по фильтрации суспензии с широким распределением частиц по размерам, которые не могут быть интерпретированы в рамках указанной модели.

II.    Математическая модель

В данной работе предлагается математическая модель, описывающая процесс фильтрации суспензии, состоящей из двух различных типов частиц, через образец пористой среды. Признаком принадлежности к определённому типу может служить, например, геометрический размер частицы. Будем пренебрегать сжимаемостью жидкости, твёрдых частиц и пористой среды. Предположим также, что физические скорости движения частиц и несущей жидкости совпадают (частицы полностью увлекаются несущей фазой). Если диаметр частиц превышает 1 мкм, то самодиффу-зией частиц в жидкости можно пренебречь [2]. Будем также пренебрегать диффузией частиц и рассматривать одномерное течение. Запишем закон сохранения массы для твёрдых частиц первого типа:

∂∂ д^ (P1№ + ^cl)) + dx (P1ciu) = 0,

где у(x ) — пористость образца, и — скорость фильтрации, oi — доля удержанных частиц первого типа, c 1 — концентрация частиц первого типа во взвеси, ρ 1 — плотность вещества частиц первого типа. Аналогично, закон сохранения массы для частиц второго типа имеет вид

(P 2^2 + УС 2 )) +    (P 2 C 2 U) = 0.

∂t               ∂x

В силу предположения о несжимаемости частиц можно в уравнениях (1) и (2) сократить плотность вещества частиц.

Закон сохранения массы для жидкости с учётом её несжимаемости принимает вид

∂ dt(^(1 - ci - c2)) +

∂

— ^{((1 -} c l ^- c 2 ^{) u )} = 0.

∂x

С учётом введённых выше обозначений имеем

У = У 0

-

σ 1

-

σ 2 ,

где ϕ 0 — начальная пористость образца.

Сложив уравнения (1) — (3) и учитывая связь (4), получим, что скорость фильтрации суспензии не зависит от координаты:

∂

и = 0.

∂x

Для замыкания системы уравнений (1), (2), (5) необходимо указать локальные законы удержания частиц каждого типа в пористой среде, а также поставить корректные граничные и начальные условия. По аналогии с работой [2] будем предполагать, что интенсивность удержания частиц в пористой среде пропорциональна скорости фильтрации и их концентрации:

∂σ i

—— = AiUCi,

∂t ^{i i ,}

где i = 1, 2, а Ai — коэффициент захвата частиц. Обозначим P — давление в жидкости, ^ — вязкость суспензии. Для описания движения суспензии через образец будем использовать закон фильтрации Дарси:

= k(^ i + CT 2 ) dP µ ∂x ^,

в котором введена зависимость проницаемости от доли захваченных частиц по аналогии с одночастичной моделью [2]:

k(^ i + 0 2 ) = k o (1 - ^CT 1 ⁺ ° 2 ) 3 .

ϕ 0

Будем рассматривать задачу закачки суспензии с постоянной концентрацией:

c i (0,t) = C in i V t> 0,

C 2 (0,t) = C in 2 V t > 0.

На образце поддерживается постоянный перепад давления:

P(0,t) = Pin  V t> 0,

P (L,t) = P out   V t> 0.

Предполагается, что в начальный момент времени образец не содержит частиц:

^ 1 (x,0) = 0, x G [0,L],

^ 2 (x,0) = 0, x G [0,L], = 1 (x,0) = 0, x G [0,L], = 2 (x,0) = 0, x G [0,L].

III.    Численная схема решения

Сформулированная математическая задача не имеет в общем случае аналитического решения. Для численного решения системы уравнений (1) — (11) вводится равномерная пространственная расчётная сетка: x , = j • h,j G [0, n — ], где L — длина образца, h — шаг сетки, N — число узлов в сетке. Конечно-разностная схема построена на основе сеточно-характеристического метода [7], суть которого состоит в сведении уравнений в частных производных к обыкновенным дифференциальным уравнениям вдоль «характеристических кривых»:

dx u dt ϕ .

Сначала на каждом временном слое по заданному полю давления вычисляется скорость фильтрации:

n     P in - P out

-

u . v^N-1 1 , hµ j=0 kn j где индекс n обозначает временной слой. Уравнение (12) получено путём суммирования по пространственной расчётной сетке дискретизованного уравнения Дарси с учётом уравнения (5). Затем находятся «характеристические кривые», вдоль каждой из которой решаются обыкновенные дифференциальные уравнения:

nn j = cn + At( - =;, И, - 1)A1 + — =; .; A2), ϕj                 ϕj

, = = + At( -- = 2 (= 2 - 1)A 2 + -; = 2, c 1j A 1 ). ϕ _j                 ϕ _j

Результатом является определение концентрации взвешенных частиц в некоторых точках образца:

x;+1=xj+—At, j j    ϕj отличающихся от точек сетки разбиения. После этого производится интерполяция величин концентраций частиц на постоянную пространственную сетку.

Последним этапом является расчёт доли удержанных частиц в каждой ячейке сетки:

n +1     n         n n +1

^ 1 j — ^1 j ^{+ A tA} 1 u ^c 1 j , n +1     n         n n +1

^a 2 j = ^a 2 j ^{+ A tA} 2 u = 2 , .

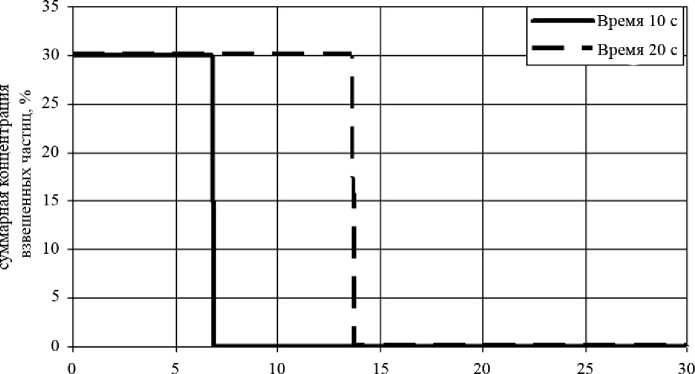
Описанная схема обладает первым порядком точности по времени и по координате и в то же время обладает особенностью достаточно точно воспроизводить разрывные решения. На рис. 1 приведен результат моделирования закачки двухчастичной суспензии в пористый образец. Параметры модели приведены в табл. 1 (№ 1). Размытие фронта составляет ноль ячеек пространственной сетки.

расстояние вдоль образца, мм

Рис. 1. Распределение суммарной концентрации взвешенных частиц вдоль образца для двух моментов времени

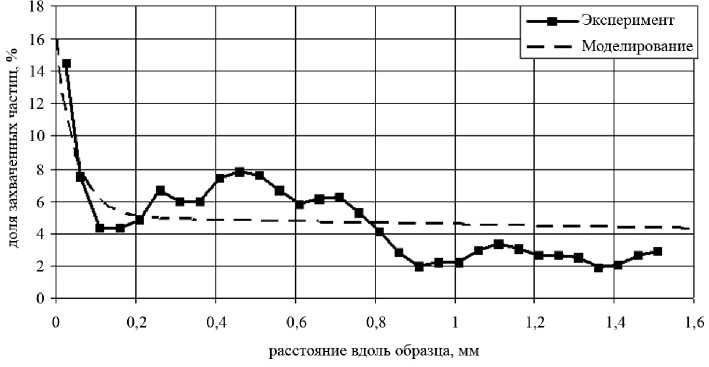
Рис. 2. Распределение доли захваченных частиц вдоль образца. Экспери- ментальные данные взяты из работы [6]

IV.    Воспроизведение экспериментальных данных

Разработанная модель была использована для моделирования процесса закачки суспензии в пористый образец. Данные, необходимые для моделирования, были взяты из экспериментальной работы [6], где приведены результаты лабораторного эксперимента по фильтрации 13 % взвеси частиц CaCO 3 через образец из песчаника.

Измеренная вязкость такой суспензии составила 30 мПа · с. Цилиндрический образец длиной 30 мм и диаметром 25,4 мм обладал пористостью 17 % и проницаемостью 600 мД. Во время эксперимента на образце поддерживался постоянный перепад давления, равный 20,4 атм.

По окончанию процесса фильтрации было измерено распределение доли удержанных частиц вдоль образца. Авторы [6] использовали одночастичную модель [1, 2] для описания результатов эксперимента. Однако, как отмечают авторы [6], не все экспериментальные результаты удалось воспроизвести в рамках данной модели.

Следуя предположению авторов [6], будем аппроксимировать распределение частиц по размерам бимодальным распределением. Коэффициент захвата частиц, очевидно, должен возрастать с увеличением размера частиц. Тогда глубина проникновения частиц должна уменьшаться с увеличением их размера. Результаты моделирования на основе двухчастичной модели приведены на рис. 2. Неизвестные параметры модели, которыми являются концентрация частиц второго типа и два коэффициента захвата, определялись на основе наилучшего воспроизведения экспери- ментальных данных. Параметры, используемые для моделирования, приведены в табл. 1 (№ 2). Результаты моделирования хорошо воспроизводят тренд в экспериментальных данных, а также излом (в районе 0,2 мм от входа в образец) на профиле распределения удержанных частиц. Они также служат подтверждением высказанного предположения, что крупные частицы удерживаются внутри образца вблизи его входа, а более мелкие частицы проходят вглубь образца.

Таблица 1

Данные, используемые для численного моделирования

№	L , см	C in l , %	C in 2 , %	Ш %	A i , 1 / м	A 2 , 1 / м	к о , Дарси	д, мПа • с	P in - P out , атм
1	3	10	20	20	0	0	0 , 6	30	2
2	3	13	0 , 1	17	70	20000	0 , 6	30	20 , 4