Моделирование динамики малого предприятия и оптимальная схема кредитования

Современная Россия характеризуется наличием предпосылок для экономического роста. Как известно, на рынке существуют спрос и предложение на товары и услуги. В ситуации, когда спрос больше предложения, нужна быстрая организация или модернизация производства. В большинстве случаев кредиты – единственная возможность получения средств на эти цели. Как известно, в РФ приняты следующие схемы кредитования [2]:

• •    с равномерным погашением кредита;

• •    с «кредитными каникулами»;

• •    «воздушный шар».

В первой схеме долг, состоящий из предоставленного кредита и процентов по нему, выплачивается равномерно одинаковыми частями в течение всего периода кредитования. Во второй схеме долг выплачивается частями после некоторого промежутка времени, называемого «кредитные каникулы». В третьей весь долг погашается одной выплатой в конце периода кредитования.

Для совместного описания схем кредитования введем параметры Θ1 , Θ2 – моменты окончания получения кредитов и окончания «кредитных каникул» соответственно. Тогда получаем задачу оптимального управления:

A F(A, 1, 2,t), maxI(A, 1 , 2 ), где A(t) – стоимость производственных фондов, I – прибыль. В работе будут конкретизированы F и I.

ПОСТАНОВКА ЗАДАЧИ

В связи с разнообразием предложений возникает задача выбора оптимальной в смысле максимизации прибыли схемы кредитования. В работе рассмотрены аннуитетные платежи по кредиту. Перечисленные выше схемы отличаются моментом начала выплат. Введем функцию кредитования, объединяющую все схемы, что позволяет свести задачу выбора оптимальной по прибыли схемы к выбору момента окончания кредитных каникул.

ПОСТРОЕНИЕ МОДЕЛИ

Для построения модели рассмотрим схему «кредитные каникулы» и применим подход, предложенный в [1]. Затраты в начале проектов, как правило, наиболее капиталоемкие. Рассмотрим линейную убывающую во времени функцию кредитования K ( t ) ^{2 K} (1 ^t ) [1], в которой 11

общий объем кредитных займов K берется в период времени (0, Θ₁]. Обычно можно заранее рассчитать Θ₁. В период (Θ₁ , Θ₂ ] предприятие развивается также без выплат по кредиту. Тогда (0, Θ₂] – период «кредитных каникул». С момента окончания кредитных каникул начинаются кредитные выплаты. По кредиту начисляются сложные проценты по ставке r за период начисления. Тогд а к моменту Θ₂ кредитная задолженность D ^{2 K} ( e^{r 1} ( r 1 1) 1)(1 r ( 2 1 )) .

r ² 1²

Введем следующие обозначения: A0 – начальная стоимость предприятия; K – весь объем кредитных займов; T – длительность периода кредитования; f - коэффициент фондоотдачи; д - коэффициент износа; коэффициент X определяет количество полученных инвестиций в отношении к суммарному объему кредитов; коэффициент 0 < £ < 1 определяет долю прибыли, вкладываемой в производство; все затраты на производство и штрафы за загрязнение окружающей среды включены в себестоимость единицы продукта Y; p — прибыль с каждой единицы продукта; J(02) - аннуитетный платеж.

Изменение стоимости фондов A(t) отражает система:

A ( t ) fe ( p- у) + (1 + 2) K ( t )-/ A ( t ) при tE (0,0 , ],

A ( t ) = A A ( t ) fe ( p- f)- a ( ( t ) при t e(0i,0 ₂ ],

e ^{( fA (} t ⁾⁽ p- /W^))- a^{( (} t ) при tE ⁽O₂ , ^T 1,

r где 5(©2) = D(r + (1 + r) T H 1 ) платеж.

аннуитетный

Решая уравнения системы (1), получим выражения стоимости фондов в любой момент времени t е [0, T ] [3]:

t e A 0 +

2 K (1 + )( . j” -1 t 01   ⁽ p ⁺®,p

1- e ,           ____

+ 7~тт) при ^{£ e}(^o,01]^, W 1P

A ( t ) =

^ ЛА* ел I 0 1 ^ t       ^ (t ®i)      / pt .   2K(1 + Л) ,e e —e e                        (

⁰    ®1 p ®p²

-) при t e(©1,0₂],

t                (t ) t pt      2K(1 + л) ,e      e - e , so(02) ,л    /?(t-r2),       .

e A_n + ---------(---+-------7---) + —^^-(1- e    ²) при t e(©„ T ],

⁰     0 1 P ©p¹        P                       ² ,

A 1 ( t ) при t е (0,0 1 ],

A ₂ ( t ) при t е (0 1 , T ].

Для схемы равномерного погашения кредита 0₂ = 0. Рассмотрим случай, когда в начальный момент времени берется один кредит K ₀ и сразу начинаются выплаты по нему в размере 8(0). При условии, что до момента 0 1 происходит модернизация производства, стоимость фондов вычисляется

„ х С A 1 ( t)~^S^0)) при ^tE (°,® 1 ], A ( t ) = I

[A ₂( t )-<^(°) при te (0 1 , T ].

Для этих двух схем в формулу общей прибыли (3) вносятся соответствующие изменения.

При вычислениях важно учитывать, что:

• •    все параметры предоставляются в расчете на период начисления процентов по кредиту;

• •    при расчетах важно проверять ограничение, что стоимость фондов в конце периода кредитования не менее некоторого, подходящего нам значения A(T) > о T = const . Это условие влияет на выбор параметра е, который следует увеличить, если условие не выполняется.

Поскольку функционал I сложен для аналитического исследования, перейдем к численному анализу.

A ( t )

где в = £Л Р - Y ) - M -

Выразим из (1) a ( t ) =

,     A -(1 + 2) K ( t )

A, (t) =---------—— при t e (0,0 ], f (p

A

^A 2⁽ t ) = —-----:---- при t e ⁽® 1, ®2^].

f ⁽ p-r)-p •

^A 3 ⁽ t ^{) =} APT^V^" при ’" ⁽⁰2 - ^{T ]}- f ⁽ p-Г)~А

Общая прибыль малого предприятия задается функционалом:

в,©

I = J (1 - E) fAt (t)(p - у) dt + J (1 - E) fA2( t)(p - Y) dt + 0

+ J (1 - E ) fA 3 ( t )( p - Y ) dt - 5 ( ® 2 )( T -® 2 ).

Подставив в (3) найденные из (2) A1, A2, A3 и f (p~ /)(1-^)

введя а =         , получим функционал для

’     е f (p-yVM’ нахождения прибыли за период кредитования:

I

_а Г A ( е в _ i) + ² K ⁽1 + 2 ) e ^e( ® , p ^- 1 + e-^e © ) + I °'                                      6Л² /3²

,     » i T-®2>1

+ e5 ( 0₂X---- в ----+ T -В 2 ) - (1 + 2 ) K I- 3 ( © 2 )( T -© 2 )

В схеме «воздушный шар» 0 ₂ = T, тогда выплата всей задолженности по кредиту D = -K^ ( e r ¹ ( r © 1 -1) +1)(1 + r ( T - 01 )) производится ^r ©1

по окончании периода кредитования. Стоимость фондов вычисляется как

РЕЗУЛЬТАТЫ ЧИСЛЕННОГО АНАЛИЗА

Рассмотрим значения параметров, которые соответствуют типичному малому предприятию, выпускающему некоторую продукцию: хлебобулочные изделия, молочные продукты и т. д. (табл. 1). Для увеличения производства берутся кредиты. Табл. 2 показывает зависимость общей прибыли от значений параметров.

Особый интерес вызывает момент, с которого наиболее выгодно начинать выплаты по кредиту. Численный анализ данной задачи показывает зависимость общей прибыли от момента 02 при различных значениях остальных параметров.

Таблица 1

Параметры задачи

Параметр	Стандартное значение	Параметр	Стандартное значение
A 0 , руб.	10 6	0 1 , мес.	6
f	0,068	02, мес.	9
ε	0,1	r % , в мес.	0,02
μ	0,0084	p	20
K , руб.	106	λ	0
T, мес.	12	λ	0

Рис. 1-2 отражают влияние выбора момента начала выплат 02 на прибыль при различных значениях процентной ставки кредита. По графикам видно, что при низкой процентной ставке выгоднее делать кредитные выплаты в конце периода кредитования (рис. 1). При большой ставке лучше начинать делать выплаты сразу по окончании процесса модернизации предприятия (рис. 2).

Таблица 2

Результаты варьирования некоторых параметров

Параметр	Стандартное значение	Интервал варьирования	Общая прибыль за период кредитования
K , руб.	106	0,5*106 – 2*106	2,773*106 – 3,821*106
Θ2, мес.	9	7–11	3,0962*106 – 3,0974*106
r % , в мес.	0,02	0,01–0,05	3,2*106 – 2,73*106
ε	0,1	0,1–0,9	3,096*106 – 1,77*105
f	0,068	0,04–0,09	1,21*106 – 4,71*106
μ	0,0084	0,04–0,1	2,4*106 – 1,45*106

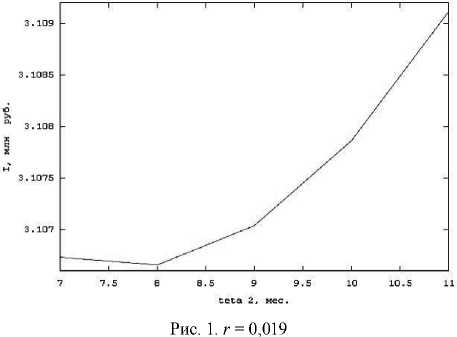
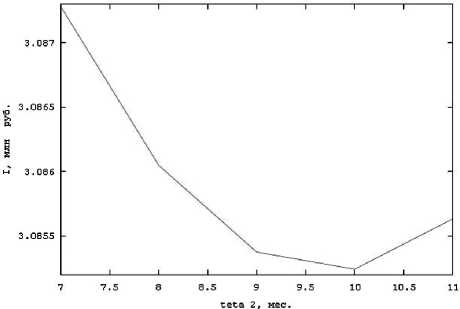
Рис. 2. r = 0,021

ВЫВОДЫ

Построенная модель динамики фондов дает возможность выбрать оптимальную в смысле максимизации прибыли схему кредитования и определить оптимальный момент окончания «кредитных каникул». Получены выражения для общей прибыли и стоимости фондов в любой момент времени, что позволяет оперативно корректировать значения параметров, определяющих развитие предприятия. Представлены результаты численного моделирования.

Имеется возможность дальнейшего развития этой модели с целью нахождения такой штрафной функции, которая позволила бы решить задачу экономического развития предприятия при ограничениях на допустимые загрязнения окружающей среды. Это дало бы подход к решению проблемы сочетания экономических и социальных интересов региона.

* Работа выполнена при финансовой поддержке Программы стратегического развития ПетрГУ в рамках реализации комплекса мероприятий по развитию научно-исследовательской деятельности.