Моделирование динамики операционного сегмента предприятия с учетом временного лага инвестиций в рабочий капитал

Данная публикация посвящена проблематике разработки экономико-математического инструментария моделирования оптимальной по рыночному критерию динамики операционного (производственного) сегмента предприятия акционерной формы собственности с учетом ограничений по внешним и внутренним параметрам и, в том числе, риску потери финансовой устойчивости, что весьма актуально для производственной корпорации, функционирующей в условиях турбулентной рыночной среды.

В методологическом плане работа продолжает исследования по динамическим моделям микроэкономики, представленным в монографии А.М. Антиколь и М.А. Халикова [1]. В этой публикации авторы приводят оригинальные модели, в которых наряду с идеями традиционных задач производственного планирования в детерминированной и стохастической постановках, изложенных в цитируемой монографии, рассматривается новый аспект – возможность учета в моделируемой динамике «затраты-выпуск» временного лага между осуществленными инвестициями в операционный сегмент предприятия и их реальной отдачей в производственно-технологическом процессе.

Объектом исследований является производственная сфера предприятия, в которой осуществляются планирование и организация основного производственного процесса, снабжение, подготовка производства и сбыт (реализация) готовой продукции.

Цель статьи – разработка и адаптация экономико-математической модели и инструментального комплекса выбора оптимального по критерию валового маржинального дохода варианта финансирования затрат и осуществления инвестиций в операционный сегмент предприятия из собственных и заемных источников с учетом параметров товарных, материальных и финансовых рынков, риска структуры капитала производственной сферы и временного лага между инвестициями в рабочий капитал предприятия и их отдачей в форме расширения базы постоянных и переменных активов, используемых в производственнотехнологическом процессе.

Материалы и методы исследования

Математический аппарат, использованный авторами при разработке методов и численных алгоритмов решения задач линейной и нелинейной оптимизации в непрерывном и целочисленном вариантах, частично заимствован из работ М. Аоки [2], Н.С. Бахвалова, Н.П. Жидкова, Г.М. Кобелькова [3], А.Ф. Грибова [17], В.А. Колемаева [8], А.А. Миролюбова, М.А. Солдатова [10], А.С. Хасанова [18], Р. Дорфмана [20], Д. Лун-бергера [22]. При разработке численного алгоритма линеаризации нелинейной дискретной модели авторы использовали идеи метода, предложенного М.А. Горским [5, 13-15].

При выборе критериев и ограничений динамической модели авторы обращались к работам Д.А. Безухова [11], М.А. Бендико-ва, И.Э. Фролова [4], М.А. Горского [14,16].

При изложении тезисов неоклассической концепции производства, эффективности производственных факторов, оценки и управления рисками производственной сферы предприятия авторы активно цитировали работы М.А. Горского [21], Г. Б. Клейнера [6], Б. Колосса [7], М. Круи [9], О.Е. Хрусталева [19], Д. Луинбергера [10] и др. авторов [23-25],

Результаты исследования и их обсуждения

• 1.    Динамическая модель производственной сферы предприятия.

Будем считать корректными следующие предположения:

• 1)    зависимость в паре «затраты – вып уск » на всех интервалах планирования (t = 1,T) являются неоклассической зависимостью:

• У , = (PK , ) " /(c , ( 1 ) ) "

или PK t = c_t ( 1 ) *y ”          (1)

где yt – выпуск в натуральном выражение; α – степень однородности производственной функции (α > 0); ct(1) – удельные затраты (затраты на единицу выпуска) для периода t; PKt – сумма постоянных и переменных активов рабочего капитала (капитал производственной сферы предприятия) на начало временного интервалаt;

• 2)    прибыль, полученная в операционном сегменте предприятия в периоде t, оценивается выражением:

PI , = ( 1 -t ) * ( ⁽p , - ^c , ( 1 ) ) *y , -

• -p , * ( 1 - k ._t ) *PK t ),           (2)

где PIt – прибыль производственного сегмента предприятия для периода t; τ – на- лог на прибыль хозяйствующего субъекта; pt – цена реализации продукции для периода t; pt – ставка по краткосрочному кредиту для периода t; ka – коэффициент автономии (доля собствеt нных средств в пассивах рабочего капитала для временного интервала t);

• 3)    рабочий капитал на начало очередного планового интервала формируется из восстановленной на конец текущего периода части и собственных инвестиций из прибыли предыдущего периода, направляемых на пополнение активов операционного сегмента (инвестиции с «задержкой (лагом) на один производственно-коммерческий цикл»):

PK t + 1 = PK t + Inv t -_p (3)

PK t = PK_t - d*PK_t = ( 1 - d ) *PK_t, (4) где d – коэффициент списания на амортизацию материальных активов рабочего капитала (принятый постоянным на всем горизонте при линейном способе начисления амортизации).

^Invt - 1 = Y t - 1 ( 1 ^-t ) * ( ⁽ P t - 1 ^- c t - 1 ( 1 ) ) *y t - 1 ^-P t - 1 * ( 1 - k . ) *PK t — 1 ),

где γt–1 – доля средств из полученной на временном интервале (t-1) прибыли операционного сегмента, направляемая на собственные инвестиции в рабочий капитал в периоде (t+1).

С учетом выражения (1) балансовое соотношение (3) запишем в виде:

c t + 1 ( 1 ) *y "+ 1 = ( 1 ^{- d} ) *^c t ( 1 ) *y " ⁺ Y t - 1 * ( ^{1 - t} ) *

* ( ⁽P t - 1 — c t - 1 ( 1 ) ) у , - 1 -P t - 1 * ( 1 — ^k a_{t - 1} ) *c t - 1 ( 1 ) *y "- 1 ).                      ⁽⁶⁾

Для первого интервала будем использовать следующее соотношение:

¹ PK y r =       ,

• cl (1)

где PKt – величина активов рабочего капитала на начало первого планового периода.

Соотношение (6) является основным, связывающим динамику выпусков для производственной сферы предприятия на последовательных временных интервалах (t–1); t; (t+1) (t≥2).

Отдельно рассмотрим случай линейной производственной функции (α=1). В этом случае соотношение (6) примет вид:

c t + 1 ( 1 ) *y , + 1 = ( 1 ^{- d} ) *^c t ( 1 ) *y , ⁺ Y t - 1 ( 1 ^{- t} ) *

* ( ⁽P t - 1 — c t - 1 ( 1 ) ) *y , - 1 - P t - 1 * ( 1 — ^k a_{t - 1} ) *^c t - 1 ( 1 ) *y , - 1 )

или ct+1 (1) *Yt+1 = (1 - d) *ct (1) *Yt + Yt-1 (1 - t) *

^C t - 1 ( 1 ) * ( (P t - 1 ^- c t - 1 ( 1 ) ) - P t - 1 * ( 1 ^{- k} a t _ , ) *Y t - 1 .                            (8)

Для повышения наглядности полученного уравнения, связывающего выпуски на временных интервалах (t–1); t; (t+1), рассмотрим важный ч аст ный случай постоянных удельных затрат на всем временном горизонте: c_t(1)=const, t = 1,T

В этом случае уравнение примет вид:

Y t + 1 =^{( 1 -} d ) *Y t ⁺ Y t - 1 ^{( 1 - T} i * ( p t - 1 - c ( 1 ) - p - 1 * ( 1 - k a t - 1 ) ) *y t - 1              (9)

Если дополнительно предположить, что все рыночные параметры производственной сферы постоянны на всем рассматриваемом горизонте p_t - 1 = p; p _t - 1 = p ; k a = k_a; y _t - 1 = Y ( t ^ 1 ) , то можно констатировать, что динамика выпусков на любых трех последовательных интервалах корректно задается однородным разностным уравнением второго порядка:

Y t + 1 ^- ( 1 ^- d ) *Y t ^-Y ( 1 ^-t ) * ( p ^{- c} ( 1 ) ^-P * ( 1 ^{- k} a ) ) *y t - 1 = 0              (10)

или

Y t + 1 ⁺ bY t ^{+ c}Y t - 1 = ⁰                                  (10’)

где b = -(1 - b); c = -Y * ( 1 -t ) * ( p - c ( 1 ) -p * ( 1 - k a ) ) .

Численный алгоритм решения однородного разностного уравнения второго порядка описан в ряде работ (например, рассмотрена работа Миролюбова А.А., Солдатова М.А.) [10]. Опишем его с некоторыми изменениями, позволяющими адаптировать к рассматриваемому уравнению (10’).

Пусть λ1 и λ2 – корни характеристического уравнения:

λ2 + bλ + c = 0           (11)

Тогда общее решение исходного уравнения (10’) может быть представлено в виде:

y_t = D 1 *X t + D 2 *X 2 .         (12)

Для нахождения D1 и D2 запишем начальные точки траектории:

y₁ = D₁X₁ + D 2 X 2 , y₂ = D^² + D 2 X 2 .

y _t = ^Y2  ^{Y1 X} 2, * X t +

^X 1 ( ^X 1 ^-X 2 )

Y i ^X i ^- Y 2

^X 2 ( ^X 1 ^-X 2 )

* X 2 =

= VD * ( Y^{2 -} Y 1 ^X 2 ) * ^X 1 ^{- 1 +} ( Y 1 ^X 1 ^- Y 2 ) * ^X 2 ^{- 1} (15)

Таким образом, соотношение (15) связывает оптимальный по критерию маржинального дохода выпуск yt с оптимальными значениями выпусков на первых двух интервалах.

Если корни характеристического уравнения (11) совпадают, то решение однородного разностного уравнения (10’) может быть представлено в виде:

y_t =X t * ( D 1 + t*D₂ ) . (16)

Также как и выше, для нахождения D1 и D2 используем данные о первых двух точках траектории:

Решая эту задачу, определим значения констант D1 и D2:

D 1

Y 2 ^- Y 1 ^X 2

X1 (X1 -^2 )

; D , =     ' - \ . (14)

X 2 ( % 1 ^-X 2 )

| Y 1 =^X * ( D 1 + D 2 ) ,         ₍₁₇₎

. Y 2 =X ² * ( D 1 + 2*D 2 ) ,

Из уравнения (11) следует, что

X₁ + X 2 = Vd , а X₁ * X 2 = c

(D – дискриминант характеристического уравнения). Получим следующее выражение для решения разностного уравнения (11):

где λ = λ1 = λ2.

Решая систему (17), найдем:

D = ^{2 X y} - ^y 2 ; d =- D = ^y₂^2 X ^y₁ . (18)

¹ X ^{2    21}     x ²

Подставим полученные значения констант D1 и D2 в соотношение (13) и получим следующую формулу для нахождения

общего решения уравнения (10’) в случае совпадения корней характеристического уравнения (11):

• У 1 = ( ^А У 1 ^— У 2 ) * ^{A t - 2}* ( 1 ^{— 1} ) , (19) справедливую для временных интервалов t ≥ 3. Кроме того, в (19) можно дополнитель-

• 1 но учесть, что A = ——b.

Стационарная (растущая или убывающая) динамика выпуска, задаваемого уравнением (10) или (10’) и описываемая соотношениями (15) – (18), возможна в случае, если дискриминант уравнения (11) неотрицателен, т.е.:

(1 — d)² + 4 y * ( 1 — t ) *

• * ( p — c ( 1 ) — p * ( 1 — k_a ) ) > 0. (20)

• 2. Практические расчеты на основе динамической модели (10)-(15).

Знак левой части неравенства (20) определяется знаком выражения, состоящего в круглых скобках. Достаточным условием стационарной динамики выпуска производственного сегмента предприятия является полное покрытие из выручки удельных производственных затрат и затрат на привлекаемый заемный капитал:

p ≥ c(1) + ρ(1 – ka), (21) что является реалистичным в условиях безубыточного производства.

Практические расчеты динамики выпусков для производственной сферы предприятия на последовательных временных интервалах, проведены для случая α = 1 и различных комбинаций управляемых параметров ka и γ (ka=0,2; 0,4; 0,6; 0,8; γ = 0,2; 0,5; 0,8) и для следующих констант: τ=0,2; p=2; c(1)=1,2; ρ=0,15; y1=10; y2=12; d=0,04. Характер динамики конечного продукта (выпуск в натуральном выражении) для различных комбинаций отражен ниже (табл. 1-12; рис. 1-12).

Динамика выпуска и рабочего капитала для α=1; ka=0,2 и γ=0,5

t	PK t	PKt	yt	Invt
1	12,00	11,52	10,00	2,62
2	14,40	13,82	12,00	3,15
3	17,15	16,46	14,29	3,75
4	24,39	23,42	20,33	5,33
5	40,26	38,65	33,55	8,80
6	77,73	74,62	64,77	17,00
7	175,72	168,69	146,43	38,42
8	466,27	447,62	388,56	101,96
9	1455,0	1396,83	1212,53	318,17
10	5349,1	5135,15	4457,59	1169,67

Динамика выпуска и рабочего капитала для α=1; ka=0,2 и γ=0,2

t	PK t	PKt	yt	Invt
1	12,00	11,52	10,00	1,05
2	14,40	13,82	12,00	1,26
3	15,13	14,52	12,61	1,32
4	17,09	16,41	14,24	1,50
5	20,39	19,57	16,99	1,78
6	25,73	24,70	21,44	2,25
7	34,34	32,96	28,62	3,00
8	48,49	46,55	40,41	4,24
9	72,47	69,57	60,39	6,34
10	114,63	110,05	95,53	10,03

Таблица 2

Таблица 1

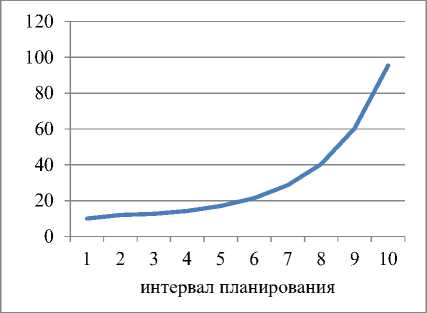
Рис. 1. Динамика выпуска и рабочего капитала для α=1; k_a =0,2 и γ=0,2

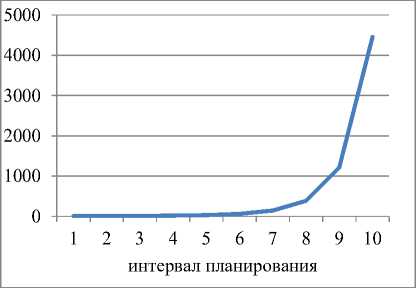
Рис. 1. Динамика выпуска и рабочего капитала для α=1; k_a =0,2 и γ=0,5

Динамика выпуска и рабочего капитала для α=1; ka=0,2 и γ=0,8

t	PK t	PKt	yt	Invt
1	12,00	11,52	10,00	4,20
2	14,40	13,82	12,00	5,04
3	19,03	18,27	15,86	6,66
4	24,53	23,54	20,44	8,58
5	53,35	51,22	44,46	18,67
6	137,72	132,21	114,76	48,18
7	450,53	432,51	375,44	157,62
8	1863,1	1788,54	1552,55	651,82
9	9784,5	9393,11	8153,74	3423,27
10	65497,5	62877,6	54581,21	22915,37

Таблица 3

50000
40000
30000
	1
•^пппп -
20000
10000
0
	1   2 3 4 5 6 7 8 9 10
	интервал планирования

Рис. 1. Динамика выпуска и рабочего капитала для α=1; k_a =0,2 и γ=0,8

Таблица 4

Динамика выпуска и рабочего капитала для α=1; ka=0,4 и γ=0,2

t	PK t	PKt	yt	Invt
1	12,00	11,52	10,00	1,11
2	14,40	13,82	12,00	1,33
3	15,19	14,58	12,66	1,40
4	17,29	16,60	14,41	1,60
5	20,86	20,02	17,38	1,92
6	26,70	25,63	22,25	2,46
7	36,28	34,83	30,24	3,35
8	52,36	50,26	43,63	4,83
9	80,23	77,02	66,86	7,40
10	130,59	125,36	108,82	12,05

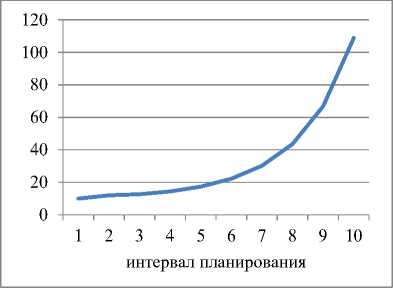
Рис. 1. Динамика выпуска и рабочего капитала для α=1; k_a =0,4 и γ=0,2

Таблица 5

Динамика выпуска и рабочего капитала для α=1; ka=0,4 и γ=0,5

t	PK t	PKt	yt	Invt
1	12,00	11,52	10,00	2,77
2	14,40	13,82	12,00	3,32
3	17,23	16,54	14,36	3,97
4	24,70	23,71	20,58	5,70
5	41,22	39,57	34,35	9,51
6	80,74	77,51	67,28	18,62
7	185,81	178,38	154,84	42,86
8	503,74	483,59	419,79	116,20
9	1611,9	1547,43	1343,25	371,81
10	6099,2	5855,23	5082,66	1406,88

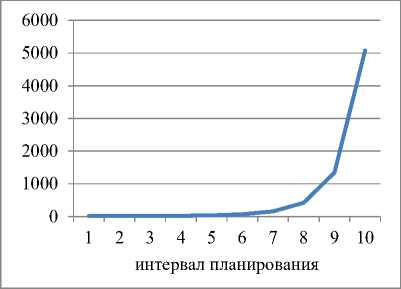
Рис. 1. Динамика выпуска и рабочего капитала для α=1; k_a =0,4 и γ=0,5

Таблица 6

Динамика выпуска и рабочего капитала для α=1; ka=0,4 и γ=0,8

t	PK t	PKt	yt	Invt
1	12,00	11,52	10,00	4,43
2	14,40	13,82	12,00	5,31
3	19,28	18,51	16,06	7,11
4	32,81	31,49	27,34	12,11
5	69,70	66,91	58,08	25,72
6	187,35	179,86	156,13	69,15
7	638,68	613,13	532,23	235,72
8	2778,48	2667,34	2315,40	1025,45
9	15487,11	14867,62	12905,92	5715,77
10	111040,6	106598,9	92533,82	40981,38

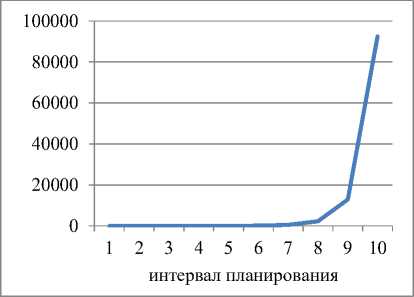
Рис. 1. Динамика выпуска и рабочего капитала для α=1; k_a =0,4 и γ=0,8

Таблица 7

Динамика выпуска и рабочего капитала для α=1; ka=0,6 и γ=0,2

t	PK t	PKt	yt	Invt
1	12,00	11,52	10,00	1,16
2	14,40	13,82	12,00	1,40
3	15,24	14,64	12,70	1,48
4	17,49	16,79	14,58	1,70
5	21,33	20,48	17,77	2,07
6	27,70	26,59	23,08	2,69
7	38,32	36,78	31,93	3,72
8	56,47	54,21	47,06	5,48
9	88,70	85,16	73,92	8,61
10	148,52	142,58	123,77	14,42

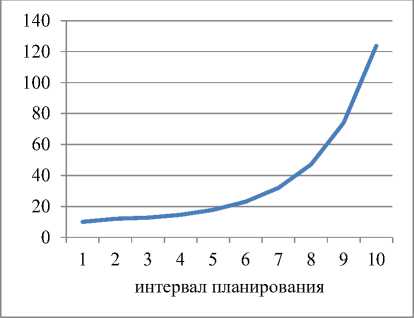
Рис. 1. Динамика выпуска и рабочего капитала для α=1; k_a =0,6 и γ=0,2

Таблица 8

Динамика выпуска и рабочего капитала для α=1; ka=0,6 и γ=0,5

t	PK t	PKt	yt	Invt
1	12,00	11,52	10,00	2,91
2	14,40	13,82	12,00	3,49
3	17,38	16,68	14,48	4,22
4	25,25	24,24	21,04	6,13
5	42,95	41,23	35,79	10,42
6	86,25	82,80	71,88	20,93
7	204,76	196,57	170,63	49,69
8	576,19	553,14	480,16	139,82
9	1925,94	1848,90	1604,95	467,36
10	7662,24	7355,75	6385,20	1859,37

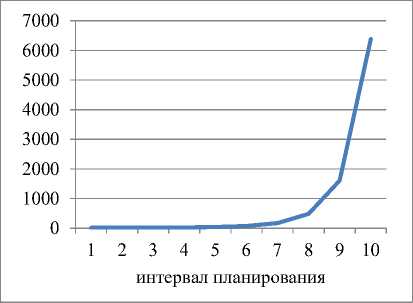
Рис. 1. Динамика выпуска и рабочего капитала для α=1; k_a =0,6 и γ=0,5

Таблица 9

Динамика выпуска и рабочего капитала для α=1; ka=0,6 и γ=0,8

t	PK t	PKt	yt	Invt
1	12,00	11,52	10,00	4,66
2	14,40	13,82	12,00	5,59
3	19,51	18,73	16,26	7,57
4	33,76	32,41	28,14	13,11
5	73,46	70,52	61,22	28,52
6	203,75	195,60	169,79	79,11
7	722,17	693,28	601,81	280,39
8	3292,89	3161,17	2744,08	1278,52
9	19397,81	18621,90	16164,84	7531,52
10	148243,8	142314,1	123536,5	57558,1

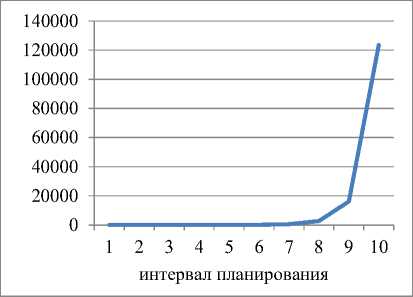
Рис. 1. Динамика выпуска и рабочего капитала для α=1; k_a =0,6 и γ=0,8

Таблица 10

Динамика выпуска и рабочего капитала для α=1; ka=0,8 и γ=0,2

t	PK t	PKt	yt	Invt
1	12,00	11,52	10,00	1,22
2	14,40	13,82	12,00	1,47
3	15,30	14,69	12,75	1,56
4	17,69	16,98	14,74	1,80
5	21,81	20,93	18,17	2,22
6	28,72	27,57	23,94	2,93
7	40,44	38,82	33,70	4,12
8	60,86	58,43	50,72	6,20
9	97,96	94,04	81,63	9,98
10	168,67	161,92	140,55	17,18

интервал планирования

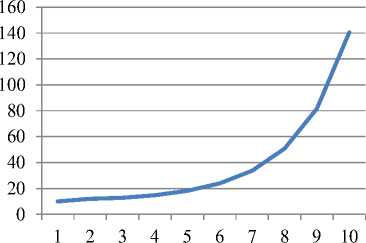
Рис. 1. Динамика выпуска и рабочего капитала для α=1; k_a =0,8 и γ=0,2

Таблица 11

Динамика выпуска и рабочего капитала для α=1; ka=0,8 и γ=0,5

t	PK t	PKt	yt	Invt
1	12,00	11,52	10,00	3,06
2	14,40	13,82	12,00	3,67
3	17,52	16,82	14,60	4,46
4	25,80	24,77	21,50	6,57
5	44,72	42,93	37,27	11,39
6	92,03	88,35	76,70	23,44
7	225,24	216,23	187,70	57,36
8	657,41	631,11	547,84	167,42
9	2293,57	2201,82	1911,31	584,10
10	9585,37	9201,95	7987,80	2441,07

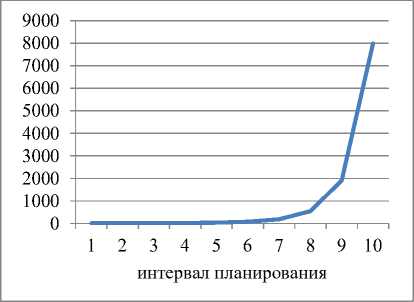
Рис. 1. Динамика выпуска и рабочего капитала для α=1; k_a =0,8 и γ=0,5

Таблица 12

Динамика выпуска и рабочего капитала для α=1; ka=0,8 и γ=0,8

t	PK t	PKt	yt	Invt
1	12,00	11,52	10,00	4,66
2	14,40	13,82	12,00	5,59
3	19,51	18,73	16,26	7,57
4	33,76	32,41	28,14	13,11
5	73,46	70,52	61,22	28,52
6	203,75	195,60	169,79	79,11
7	722,17	693,28	601,81	280,39
8	3292,89	3161,17	2744,08	1278,52
9	19397,81	18621,90	16164,84	7531,52
10	148243,8	142314,1	123536,5	57558,14

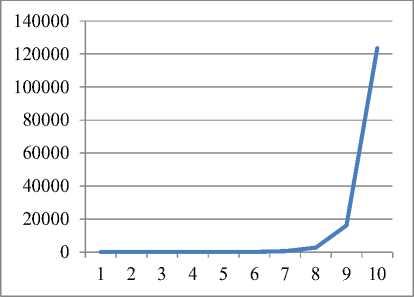
Рис. 1. Динамика выпуска и рабочего капитала для α=1; k_a =0,8 и γ=0,8

Выводы

Анализируя результаты практических расчетов по динамической модели, сделаем следующие выводы:

– доля собственных инвестиций в рабочий капитал операционного сегмента предприятия – управляемый параметр, существенно влияющий на динамику выпуска, что отчетливо прослеживается по приведенным таблицам и графикам;

– чем выше доля средств, направляемая на собственные инвестиции в рабочий капитал, тем меньшее влияние на динамику выпуска оказывает коэффициент автономии (доля собственных средств в пассивах рабочего капитала);

– зависимость динамики «коэффициент автономии – темп роста выпуска» яв- ляется прямо пропорциональной: с ростом коэффициента автономии растет и темп выпуска продукции, причем, весьма значительно. Данная взаимосвязь особенно прослеживается для случая γ = 0,8 (таблица 12, рис. 12).

Последний вывод особенно важен в свете рассматриваемого варианта модели операционного сегмента с учетом временного лага инвестиций в рабочий капитал предприятия; модели динамики операционного сегмента с «временным лагом» существенно отличаются от моделей динамики без его учета (модели без учета временного лага и соответствующие им расчеты динамики в паре «затраты-вы-пуск», подтверждающие этот вывод, приведены в работе Безухова Д.А. [11]).