Моделирование динамики производственных процессов на ЭВМ

Любое промышленное предприятие как объект моделирования является исключительно сложной системой. Процесс изготовления изделий характеризуется прежде всего движением во времени и пространстве большого числа материальных, трудовых, финансовых и информационных потоков, связанных с подготовкой производства, доставкой материалов и энергии, выполнением множества технологических операций и операций по обслуживанию производства, хозяйственно-финансовому обеспечению, сбыту и реализации продукции. Для экономических объектов более выраженной является стохастическая составляющая процессов поведения (заявки потребителей на продукцию, поставки сырья, материалов и энергии, положение на фондовых рынках и т. д.).

Решение вопросов рационального использования материальных и трудовых ресурсов, повышения эффективности работы оборудования требует повышения научной обоснованности методов управления производством. Создание конкурентоспособной новой техники связано с выполнением различных многовариантных решений. В этих условиях требуется переход к широкому использованию экономико-математических методов и моделей.

Современные информационные технологии привели к бурному развитию нового направления исследования сложных производственных процессов — имитационному моделированию, широко и давно используемому при исследовании различных технических объектов. Суть метода имитационного моделирования состоит в том, что вместо аналитического описания статических взаимосвязей между входами, выходами и состояниями разрабатывается алгоритм, отображающий последовательность развития процессов внутри исследуемого объекта. Для имитационного моделирования характерно отображение элементарных процессов, составляющих исследуемый объект, с сохранением логической структуры моделируемого объекта и последовательности протекания процессов во времени. ^

В зависимости от вида исследуемого объекта, решаемых задач и целей исследования имитационные модели могут быть ориентированы на- отображение процессов различной природы: статических и динамических, детерминированных и стохастических, дискретных и непрерывных, линейных и нелинейных, стационарных и нестационарных.

Для формализации элементов сложной системы необходимо иметь математическую схему описания всего многообразия перечисленных выше процессов, учитывающую также действие случайных факторов. Процесс разработки формализованной схемы исследуемого объекта включает несколько этапов: 1) структуризация объекта на отдельные модули; 2) представление модуля в виде конечного множества элементов — элементарных процессов; 3) представление схемы взаимодействия элементов в модуле — схемы соединения; 4) выбор математической схемы для формализованного описания работы каждого элемента и модуля в целом; 5) формирование входной и выходной информации для каждого элемента и модуля в целом; 6) выбор методов математического расчета элементарных процессов.

В качестве математической схемы формализации элементарных процессов могут быть использованы: О дифференциально-разностные и интегральные уравнения; 2) теория массового обслуживания., марковские процессы; 3} теория игр и планирование экспериментов; 4) теория случайных процессов и теория статистического моделирования; 5) теория автоматов и математическая логика; 6) теория графов.

К математическим методам расчета элементарных процессов относятся: t) численные методы решения систем алгебро-дифференциальных и интегральных уравнений; 2) методы расчета марковских случайных процессов, моделирование процесса обслуживания, расчет

характеристик систем массового обслуживания; 3) методы идентификации случайных процессов, методы оценивания параметров распределения случайных величин, методы Монте-Карло; 4) методы описания дискретных детерминированных процессов с использованием теории конечных автоматов; 5) методы описания дискретных стохастических процессов с использованием теории вероятностных автоматов.

В работе описывается программа, предназначенная для моделирования детерминированных непрерывных процессов производственных систем. Формализованная математическая модель представлена в виде системы алгебро-дифференциальных уравнений, при формировании которой используются следующие элементарные процессы:

Процесс накопления. В процессе производства имеется изменение уровней запасов материалов, комплектующих, оборудования, денежных и других средств. Для непрерывного процесса математическим аналогом операции накопления является операция интегрирования во времени:

У(0 = f (х„ (0 - ^ (ON + у.;

°            . .                     °)

о^у(О<У™; |х(0|^^- где у(t) — количество продукта в накопителе (на складе);

^н/™=^ — соответственно входной и выходной потоки в Накопителе;

Уо — начальное* значение запасов на складе;

• У™ ~ ёмкость Накопителя;

Х^ — Максимальная пропускная способность канала передачи.

Если процесс производства является существенно дискретным, то значение переменной На п + i Шаге определяется разностным урав-нёйИёМ:

У_п», = «Л <*„ " ^K,J^h-           (2)

где й — шаг дискретизации

Процесс подготовки. Представляет собой Последовательность Операций изготовления и обработки некоторых компонентов изделия. Подготовительная операция в непрерывном процессе представляется инерционным звеном первого, второго или третьего порядка. Например, передаточная функция звена первого порядка в операторной форме имеет вид:

где и_{в /вых} — соответственно, количество входного /выходного продукта;

Г — постоянная времени в первом приближении обратно пропорциональна количеству рабочих К, занятых на подготовительной операции, и их производительности труда F; Т = 1 / KF;

к — коэффициент передачи звена.

Процесс объединения. Характеризуется наличием нескольких переменных на входе и одной переменной на выходе. Например, из некоторого количества исходных деталей собирается одно изделие. В первом приближении операция сборки может моделироваться инерционным звеном первого, второго, третьего порядка. Уравнение звена первого порядка в дифференциальной форме имеет вид:

^■^y^M^-vO)),       (4)

где о(0 — количество выходного продукта; //О — t-ый вид входных комплектующих компонентов;

s — дискретная переменная принимает значения s — 1 только в том случае, если на сборку поступают все виды комплектующих компонентов, иначе s = 0.

Процесс передачи (транспортные ком.' муникации). Имитируют движение материальных потоков (и нематериальных —- финансовых, информационных и т, д.), В общем случае операция передачи определяется функцией запаздывания:

w™i(0=/(^('-"О).                (5)

где т — запаздывание транспортной операции.

Уравнение потоков в упрощенном виде можно задать в форме дифференциального уравнения для инерционного звена, например, первого порядка:

%^ = 7 (Ь. (0-^0».      (6)

at 1

На основе приведенных элементарных процессов можно отобразить в допустимых рамках достоверности следующие модели: технологический процесс по изготовлению некоторой продукции, динамику использования трудовых ресурсов, накопление и использование финансовых средств, движение информационных потоков в системе управления объектом и т. д. а

Кроме уравнений приведенных элементарных процессов, в модели могут использоваться дополнительные уравнения по согласованию и приведению к сопоставимому виду уровней накопителей и значений потоков различного назначения. Например, модель содержит две подсистемы: моделирование технологических процессов изготовления изделий и моделирование процессов движения исполнителей.

Сопоставить переменные этих подсистем можно через коэффициент, соответствующий производительности труда. Достоверность отображения динамических характеристик объекта зависит от возможности учета запаздываний.

Следует отметить, что наиболее трудоемким является этап построения формализованной модели, требующий от пользователя высокого профессионализма, знания объекта Моделирования, правильного формирования целей и задач исследования, формирования плана проведения экспериментов на модели.

Используемая система позволяет моделировать непрерывные и дискретные детерминированные процессы. Система имеет средства графического отображения процессов, средства обработки результатов моделирования (разложение в ряд Фурье, расчет средних на заданном интервале и т. д.), пользовательский интерфейс на основе текстового входного языка. Ведется разработка графического представления формализованной модели объекта.

Выполнение заказов за счет запасов т 11, Т 12

Ув

Оформление заказов на материалы Т3 Т4 Т41

Х,4

£15

Х32

*35

Уз io

Х37

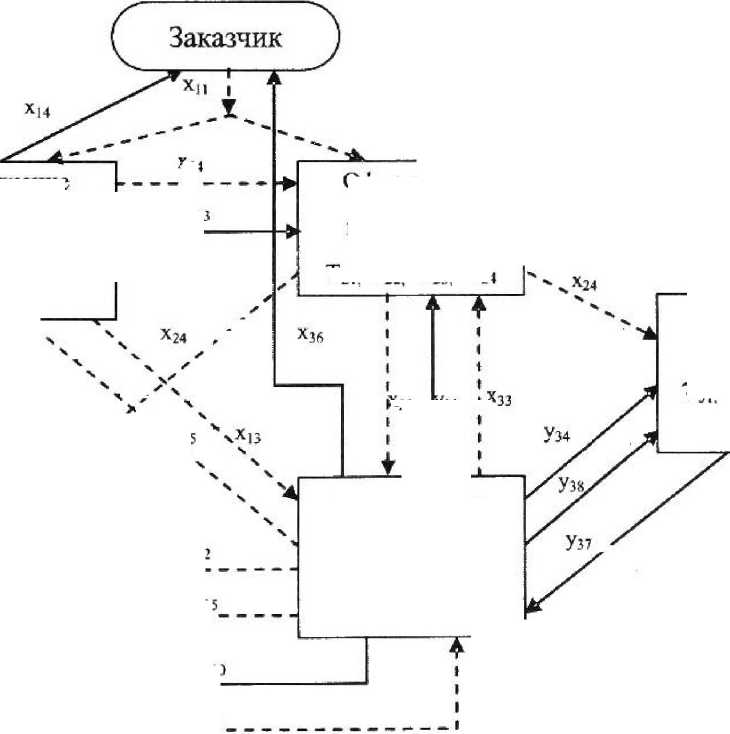
Рисунок 1 Структура модели

Оформление заказов на возмещение запасов Т21. Т22, Тзз, Тм

►43

/32 1

Производство Т 32, ^ 33, F

Управление численностью рабочих

Т51. Т 52, Tsi, Т52

Для иллюстрации возможностей программы взята модель предприятия [1] Модель отображает процессы взаимодействия предприятия с заказчиками, процесс производства, поставку сырья и материалов, изменение численности рабочих и некоторые финансовые показатели.

Представленная модель выполняет заказы по двум каналам — за счет отгрузок товаров со склада готовой продукции и непосредственно с производства.

Реализуемая модель содержит следующие подсистемы (рис. 1): 1) первая подсистема выполняет заказы покупателей за счет запасов и распределяет части заказов на производство; 2) вторая подсистема описывает процесс оформления заказов на возмещение запасов на складе готовой продукции; 3) третья подсистема описывает процесс производства по заказам покупателей, а также по заказам на возмещение запасов; 4) четвертая подсистема описывает оформление заказов на основные материалы; 5) пятая подсистема описывает процессы регулирования численности рабочих.

На рис. 1 стрелками изображены информационные и материальные потоки между подсистемами модели:

— Хц — поток заказов, поступающих на за-

Менеджмент и маркетинг в организациям вод;

— хм — отгрузка продукции из запасов завода;

■— Л36 — отгрузка продукции по заказам покупателей с производства;

— у]3 — фактический запас продукции;

— у3? — численность рабочих на заводе.

В качестве параметров модели задаются постоянные времен Т инерционных звеньев, отображающих ту или иную операцию. Производительность труда на заводе F, время запаздывания т.

На рис. 2 приведен пример расчета динами- : ки процессов с использованием разработанной программы.

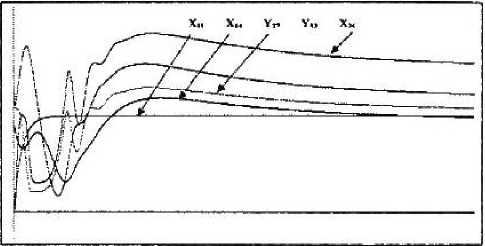
Рисунок 2

Расчет динамики процессов производственной системы