Моделирование динамики регулируемого гидромотора

Введение . Интенсификация режимов технологических машин-автоматов требует расширения диапазона регулирования скорости гидроприводов вращательного движения. При этом возникает необходимость обеспечения статической и динамической точности процесса регулирования аксиально-плунжерного гидромотора [1–3]. Для проектирования гидроприводов с наклонным блоком цилиндров необходимо разработать математические модели, позволяющие адекватно описывать переходные процессы, возникающие при изменении режима работы гидроприводов.

Характер переходного процесса во многом определяется физическими процессами в качающем узле и регуляторе рабочего объема гидромотора [4, 5].

Цель работы. Исследование динамических процессов объёмного гидропривода с наклонным блоком цилиндров и дискретным регулированием гидромотора.

Условия и методы исследования . Объектом исследований выбран регулируемый гидромотор, при-веденый на схеме гидропривода (рис. 1).

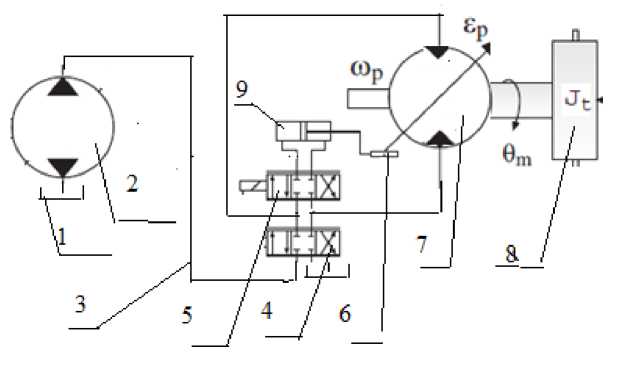
Рис. 1. Гидросхема гидропривода с регулируемым гидромотором

Исполнительным механизмом системы управления служит аксиально-поршневой регулируемый мотор. Мотор состоит из блока регулятора и качающего блока. Качающий узел преобразует энергию давления рабочей жидкости в крутящий момент на валу гидромотора. Распределитель служит для изменения рабочего объема гидромотора посредством изменения угла наклона блока цилиндров.

Для анализа и исследования динамических процессов в гидроприводе использовано имитационное моделирование. Математическая модель гидропривода представляет собой совокупность уравнений, записанных для отдельных его элементов. В гидросистему включается дополнительная электрическая цепь, представляющая собой первую ступень усиления (первый каскад) сигнала. Входной сигнал представляет собой электрический сигнал малой мощности, поэтому его необходимо усилить, чтобы он после преобразования в механический мог перемещать золотник гидрораспределителя.

Условием срабатывания автоматической системы управления является

R ₂

^E 2 = _D ^E 1 ,

R ₁

где E 1 , E 2 – электрическое напряжение на входе и выходе сигнала; R 1 , R 2 – сопротивление на входе и выходе сигнала.

Если это условие нарушается, то появляется напряжение, которое после усиления приводит в движение сервозолотник гидрораспределителя, направляющий поток рабочей жидкости в нужную полость гидроцилиндра. Перемещение штока гидроцилиндра, связанное с потенциометром, происходит до тех пор, пока не будет уравновешено входное напряжение, т.е. пока напряжение в точке сравнения вновь не станет равным нулю. Таким образом, мы имеем здесь потенциометрическую обратную связь.

Уравнение напряжений в электрической цепи магнита [2]

U

dI у dx я ус ■ R у I у+Ly IT + Ск ~л ■

где U ус – напряжение на выходе электронного усилителя; R y – активное сопротивление обмотки управления электромагнита; L y – индуктивность обмотки управления электромагнитом; C к – коэффициент противо-ЭДС; x я – смещение якоря электромагнита золотника.

После преобразований уравнение цепи управления ЭМ будет иметь вид

T  —y- + i = k. • U упр dt y iu y

Из уравнения цепи управления электромагнита следует, что передаточная функция цепи управления электромагнита будет следующей:

W(s) = ^k Fi ' k u

^Tупр • s ^{+ 1}

.

L

Здесь T =----y--постоянная времени передаточной функции цепи управления электромаг-упр   Ry + Reax нита, где Ly – индуктивность обмотки управления электромагнита; Ry – активное сопротивление обмотки

электромагнита; R вых

тромагнита; k u =

– сопротивление выходного каскада электронного усилителя; k Fi – постоянная элек- 1

– коэффициент передачи электронного усилителя.

R y + R в _Ы х

Расход жидкости через канал в золотнике [2]

^QKaH = V

кан

• ^{П d}цу 2

• §•

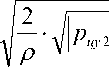
^- Р сл\ • sign ( Р цу 2

- ^рсл ) ,

где µ кан – коэффициент расхода канала в золотнике; d цу2 – диаметр золотника; δ – зазор между гильзой гидроцилиндра и поршнем; ρ – плотность рабочей жидкости.

После преобразований передаточную функцию для золотника запишем в виде

W ( s ) =        ’

T ₃ s + 1

^F3 + ^kQp^kmp3

где T₃ =-------- y --постоянная времени передаточной функции основного золотника; ^kQP y • ^Сз

F3 • kQx k3 =------— - коэффициент усиления передаточной функции основного золотника.

^kQ_Py • ^Сз

Уравнение движения поршня гидроцилиндра имеет вид [2]

d2 z          dz m —цс + к  —— + P = p F ц. с dt 2       mp. ц. с dt нагр p пор порш

-

P F , pшт шт ,

где m ц.с – приведенная масса поршня и подвижных элементов силового гидроцилиндра; k тр.ц.с – коэффициент вязкого трения в гидроцилиндре; P^Σ нагр – внешняя нагрузка, действующая на шток; F шт – площадь, равная площади поршня гидроцилиндра за вычетом площади штока; F порш – площадь поршня; p пор – давление в поршневой полости гидроцилиндра; p шт – давление в штоковой полости гидроцилиндра, z ц.с – перемещение поршня силового цилиндра. Отсюда передаточная функция давления в силовом гидроцилиндре

W p ' ^s ) = тЪ’

^Т рцс s + ¹

Vс где T с =-----ц--постоянная времени передаточной функции давления силового гидроцилиндра. рцс ж Qp

Математическая модель гидромотора [2]

dP ( t ) dt

a p

K

K упр

р (t) - к^ ^„(t)+-p- u (t) упр               упр da^t) = q bp р(t) — b^^ (t) + Xмн(t) dt I b            I b           I b

где P(t) - гидравлическое давление потока жидкости; u(t) - управляющее воздействие; а _гм ( t ) - скорость вращения вала гидромотора; К_упр – коэффициент упругости трубопровода с жидкостью передающей гидравлической линии; a_р – коэффициент, учитывающий потери давления в гидравлической линии при передаче потока жидкости; q_н – максимальный рабочий объем насоса; q_гн – максимальный рабочий объем гидравлического двигателя питателя; I_в – приведенный к валу двигателя момент инерции; b_гм – коэффициент гидромеханических потерь, зависящих от условной скорости; b_p – коэффициент гидромеханических потерь, зависящих от давления на входе гидромотора.

Расход на входе гидромотора

Q c =

Vqn

1000 7,’

где Vq – вытесняемый гидромотором объем за один оборот; n – частота вращения вала гидромотора; ή v – объемный КПД гидромотора.

Выходной крутящий момент

_М = Vq ∆ рn , ^c   20 π

где Δр – перепад давлений на входе и выходе гидромотора. Выходная мощность

_Р = Q _с ∆ рn ^c 600

.

Частота вращения n= Qc1000η

Vq

.

На рисунке 2 приведены результаты моделирования гидропривода с регулируемым гидромотором.

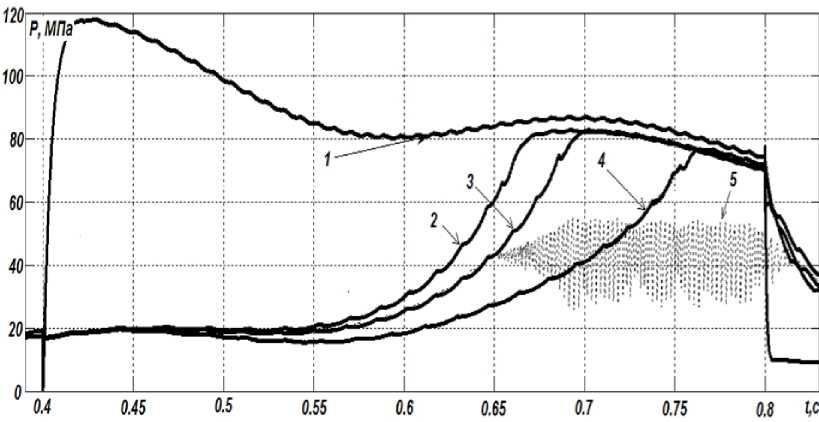
Рис. 2. Результаты моделирования гидропривода с регулируемым гидромотором

Зависимость 1 иллюстрирует изменение давления в напорной линии в предположении мгновенного изменения рабочего объема. Это приводит к резкому увеличению крутизны фронта нарастания давления и пикового давления в напорной линии. Зависимости 2, 3 иллюстрируют нарастание давления при реализации механизма жидкостного трения и конечной скорости изменения объема гидромотора при различных диаметрах поршня гидроцилиндра блока регулятора объема: d 1 = 2,6 см; d 2 =1,8 см – для кривой 2; d 1 = 2,2 см; d 2 =1,8 см – для кривой 3. Зависимость 4 – при реализации механизма смешанного трения, что существенно увеличивает время изменения объема гидромотора. Зависимость 5 моделирует включение переливного клапана

Заключение

• •    Математическая модель гидравлического регулятора позволяет моделировать переходные процессы, связанные с изменением режима работы гидропривода.

• •    Результаты моделирования динамических процессов в гидроприводе позволили установить минимальную величину времени срабатывания гидравлического регулятора при дифференциальном подключении гидравлического регулятора к напорной гидролинии и выполнении условия d 1 / d 2 = 2 , время срабатывания на уменьшение рабочего объема и его увеличение одинаково.